基于遗传算法的公交车调度优化研究

谭华

（桂林航天工业学院，广西 桂林541004）

公交调度管理是公交企业运营和业务管理的核心，对公交调度机制进行优化，建立合适的公交调度方案，可以有效地提高城市公交运营水平和服务质量，但长期以来，我国很多城市的公交企业在制定公交运营方案时，主要依靠管理人员经验和直觉，导致公交运行水平和服务质量都很低下，从而影响民众公交出行的使用比例和公交企业的经济收益。所以，通过对公交车调度的研究可为现代化公共交通提供技术支持和服务保障，实现公交调度运营的高效率、高效益，为乘客提供准时、快速和舒适的服务，提高公共交通的吸引力，从而提高企业的经济效益，方便居民出行。

鉴于此，大量国内学者从不同角度对公交车调度问题进行了研究，例如，2016 年丁勇等[1]针对泰州市公交智能化建设方面存在的技术问题，采用基于遗传算法对泰州市的公交调度问题进行了研究；2017 年韦尚成[2]提出了一种临界- 遗传算法对公交调度问题进行了研究；2017 年邓芳玥[3]采用改进遗传算法对公交线路调度模型进行了研究；2019 年武斌[4]研究了公交调度的模糊多目标规划模型，并通过遗传算法验证了模型的合理性。同年，彭蝶飞[5]等根据景区现有的公共交通资源和旅客的出行规律，构建了以旅游公交营运成本、游客等待成本和游客流失成本三方面优化目标的模型，并通过遗传算法进行了验证研究。2020 年徐晨畅等[6]提出了一种应对突发交通状况的公交智能调度算法，并通过遗传算法进行了求解验证。

本文在总结和分析前人对公交调度问题的研究方法后，以南宁市某一公交线路为例，根据其日平均客流情况，建立了该线路的公交调度优化数学模型，最后，通过遗传算法求解得到该线路公交车的最优化发车时间间隔及配车数量。研究表明，采用优化后的公交调度机制，能有效降低公交运行成本和提高乘客满意度。

1 数学模型的建立

1.1 模型假设

公交调度的数学模型主要是对实际公交调度问题的抽象和概况，因此不可能完全考虑到所有的复杂外部因素，必须合理的对外部因素做相应的限制，公交车的调度模型，具有复杂和受外部影响因素多的特点，对此，本文进行了如下假设：

（1）公交车辆为同一车型，且公交车运行情况良好；

（2）乘客到达站点数量服从均匀分布；

（3）乘客上车的时间可以忽略不计；

（4）公交车只运行一条公交线路上，且只考虑单程车运行；

（5）乘客消耗的单位时间费用是固定值；

（6）公交车辆单位乘次运营成本是固定值；

（7）全程实行统一票价。

1.2 目标函数及约束条件

在实际的公交调度中，公交车辆调度优化的目标函数，需要从乘客利益和公交公司利益的角度来考虑，从公交公司的角度，需尽量大的发车间隔以减少发车次数，从而降低运营成本来提高公司的收入，从乘客的角度，需要尽量小的发车间隔，以最大限度地降低因等车和换乘带来的交通费用损失。

本文根据公交运营时间及乘客到站密度情况，将公交车运营时段进行分时段处理，为了建立易于求解的优化模型，我们将该公交该线路的发车时段分为若干个高峰时段和若干个平峰时段。以全天公交公司运营成本和乘客等车损失费用的总和最小为优化目标，分别建立高峰时段和平峰时段的目标函数及约束条件。

其中，高峰时段的费用函数f1如（1）式所示：

考虑到公交公司利益，这里我们以公交车平均满载率不低于60%为目标函数的约束条件，如下（4）、（5）式所示：

以上数学模型中符号说明如下表1 所示：

2 基于遗传算法的公交调度优化模型求解

2.1 遗传算法求解概述

遗传算法[7]（Genetic Algorithm, GA）是由美国密歇根大学的John H. Holland 教授及其学生于20 世纪60 年代末到70 年代初提出的。是模拟达尔文生物进化论的自然选择和遗传机理的生物进化过程的计算模型算法。自其诞生以来就受到许多学者的关注。经过多年的不断发展，在基础理论和算法设计研究上都取得了长足的进步，尤其是在越来越多的领域中得到成功应用。其中在公交调度优化方面也有着十分广泛应用，这里也借助遗传算法对公交调度优化目标函数进行求解。

2.2 模型的遗传算法求解步骤

遗传算法求解的基本步骤：

（1）首先是编码，一般采用二进制编码或实数编码把问题的解表示成“染色体”（个体）；然后进行种群初始化，就是依据编码规则给出种群的初始解，也即随机产生一群“个体”。

（2）计算适应度，即根据适应度函数计算每一个个体的适应度值，然后按适者生存的原则，从中选择出适应度较大的“个体”进行复制，再通过交叉、变异过程产生更适应环境的新一代“个体”种群，即子代。

（3）重复第2 步。

（4）经过这样的一代一代地进化，达到终止条件，最后就会收敛到最适应环境（适应度最大）的一个“染色体”（即个体）上，那它就是问题的最优解。图1 所示，给出了基本遗传算法求解流程图。

图1 基本遗传算法求解流程图

①编码。编码是设计遗传算法首要解决的问题。选择合适的编码方式，对问题的求解精度有非常关键的影响，由于二进制编码的随机性使得其局部搜索能力较差，尤其在高精度的问题上不够理想，鉴于此，本文采用实数编码的方法，在这种编码方法中，染色体的各个基因就是决策变量的真实值。每个染色体代表一个时间段的发车间隔。

②初始种群。在本文中，根据经验法，初步选择初始群体中的个体值。对于高峰时段的初始值可以选择[5,15]区间的任意值作为初始值，对于平峰时段可以选择[15,30]区间的任意值作为初始值。

③适应值函数。遗传算法的适应度是用来判断群体中的个体的优劣程度的指标，它是根据所求问题的目标函数来进行评估的。这里直接以待求解的目标函数转换为适应度函数，该公交调度模型的目标函数为最小化问题，所以适应度函数为fD=min（mf1+nf2）

④算子选择。遗传算法的操作算子有选择、交叉和变异这三种，它们分别模拟了生物繁衍、交配和基因突变。在选择算子方面，我们这里采用轮盘赌选择算子；在交叉算子方面，我们采用算术交叉算子，在变异方面，我们采用均匀变异算子。

⑤终止条件。设定最大的进化代数，当遗传算法运行到该参数指定的世代，计算终止。

3 实例分析

本研究以南宁市某一条公交线路为研究对象, 对该线路上行方向的发车时刻表进行优化。如图2 所示是该线路每日的平均客流变化情况。该公交线路全长16.2 公里，30 个站点，固定发车时间间隔为15 分钟，实行统一票价（2 元/人），该线路运营时间为6:30-21:30（共15 小时）。

图2 公交线路平均日客流情况

这里我们将公交车一天的运行时间分为9 个时段，又考虑到，公交发车一天内的发车间隔在个时段内不会频繁更换，将该线路一天的发车时段用高峰时段、平峰时段进行标记，如表2所示。最终客流平峰时段为：6:30-7:30、8:30-12:00、12:30-14:00、14:30-17:30、18:30-21:30，共12 个小时。高峰时段为：7:30-8:30，12:00-12:30，14:00-14:30，17:30-18:30，共3 个小时。

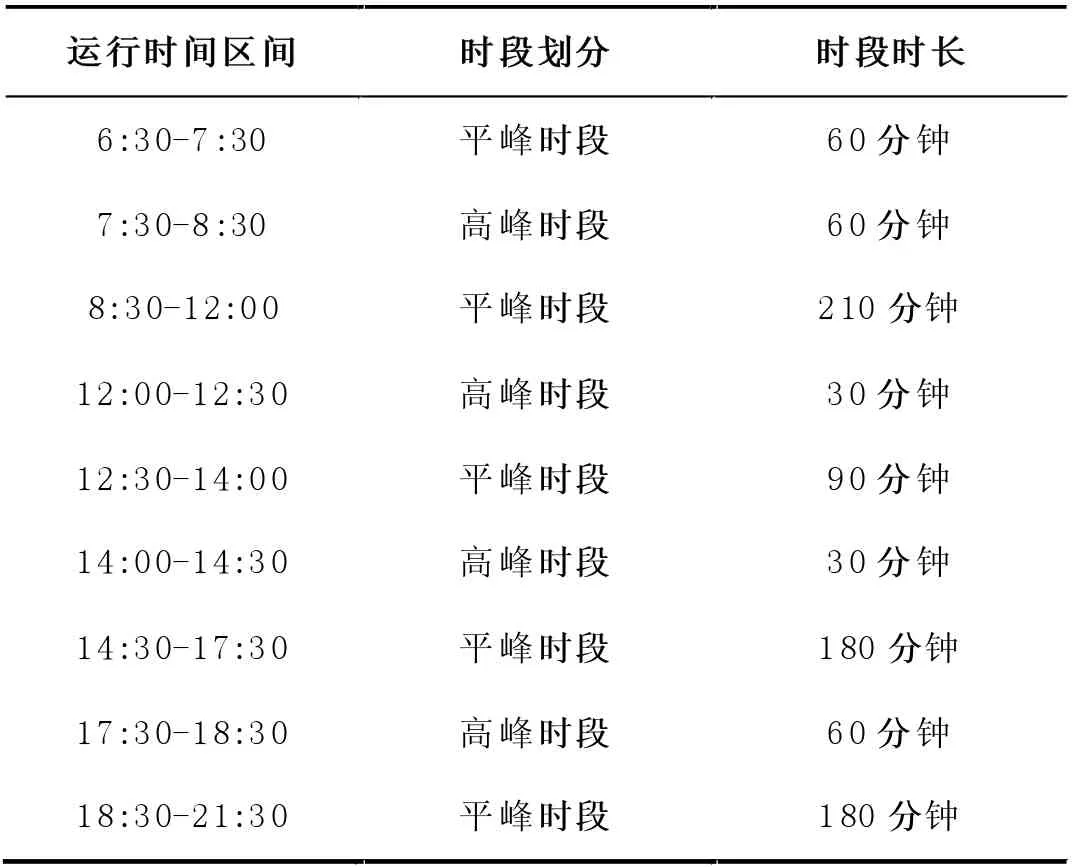
表2 运行时间区间及各时段划分

根据建立的公交优化数学模型，采用遗传算法进行仿真求解。算法中需要的主要参数：发车间隔变化区间[5，30]，且取值为0.5 的整数倍。初始种群规模N=20，交叉概率Pc =0.9，变异概率Pm =0.01，最大迭代次数G=200。高峰时段费用损失权重系数为0.6，平峰时段费用损失权重系数为0.4，高峰时段第j 车站乘客到达率为0.85，平峰时段第j 车站乘客到达率0.55，高峰时段公交公司费用消耗的加权系数0.7，高峰时段乘客等车的费用损失加权系数0.3，平峰时段公交公司费用消耗的加权系数0.6，平峰时段乘客等车的费用损失加权系数0.4。

最后，通过仿真求解，得到南宁市该路公交车的优化发车时间间隔，高峰时段的优化间隔时间为8.3 分钟，平峰时段的优化间隔时间为17.8 分钟，为了考虑到实际发车间隔一般为5 的倍数，同时一天的发车时刻表不会频繁更换，最终得到了次优化的发车间隔，高峰时段发车间隔为10 分钟、平峰时段发车间隔为20 分钟，这样使得总发车趟数为54 趟、满客率平均为80%，公司运营成本节约10%，乘客满意度提高20%。

4 结论

本文针对南宁市某一公交线路的公交调度问题进行了研究，建立了该线路的公交调度优化数学模型，通过遗传算法求解得到该线路公交车的最优化发车时间间隔及配车数量。研究表明，采用优化后的公交调度机制，能有效降低公交运行成本和提高乘客满意度。利用本文建立的公交调度模型，对其他公交线路的调度优化有一定的借鉴意义和参考价值。