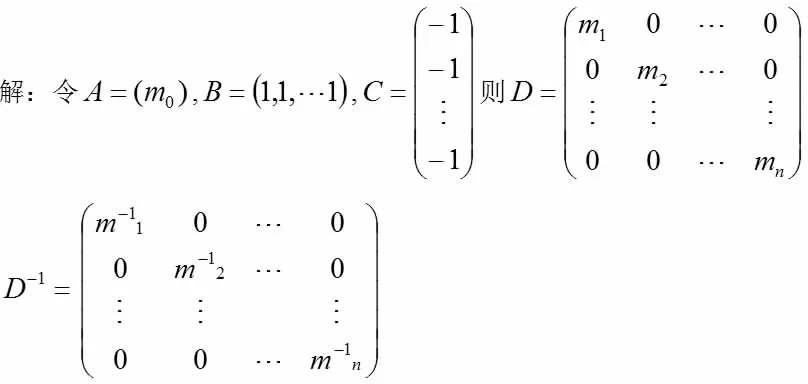求一些特殊类型分块矩阵的行列式

韩荣梅

（内蒙古科技大学包头师范学院数学科学学院，内蒙古 包头014000）

矩阵在数学的很多学科上例如线性代数、线性规划、组合数学等有着重要的使用价值，此外，在实际生活中的很多问题也可以抽象成矩阵进行表述和运算，因此矩阵的运算以及矩阵的应用，都值得我们去深入研究。当矩阵的行的个数和列的个数都比较多时，这时研究矩阵的计算过程会有些复杂，为了让我们更清楚阶数更高的矩阵的结构，为了简化其运算，我们可以通过把高阶矩阵采用分块的形式来达到我们的目的，从而使有关矩阵的理论问题和实际问题都变得更加容易，这时就体现出了分块矩阵的重要性。矩阵分块，就是把一个行数列数较多的矩阵看做是由一些小的矩阵组成。就如矩阵的元素（数）一样，特别是在运算中，可以把这些小矩阵算作数一样处理。把矩阵分块后再进行相应的运算会更加方便，因为利用矩阵的分块可以更加清楚矩阵间的某些联系，使得计算非常方便，方法容易总结，是处理级数较高的矩阵时常采用的方法。

分析：观察该行列式发现除对角元素外，其余元素都相同，所以可以用加边法升阶后对行列式进行化简，对化简后的矩阵再进行分块计算出行列式结果。

解:对原行列式运用加边法，然后将加边后的行列式的第一行乘-1 倍加到其余各行，得：

分析：观察矩阵，根据做题习惯很容易将矩阵分块为A，B，C，D 四个小矩阵，又已知矩阵D 可逆，故由定理1 可以直接计算出矩阵M的行列式。