曲线正矢总和与偏角及测点距之间的几何关系应用分析
2020-11-05俞友强中国铁路上海局集团有限公司金温铁路有限责任公司
俞友强 中国铁路上海局集团有限公司金温铁路有限责任公司
各类教材、规范对曲线计划正矢的计算过程进行了叙述,但未提及正矢总和、偏角和测点距三者之间的几何关系计算,给曲线正矢及拨道量计算造成一定困惑。通过建立曲线正矢总和(Σf)、偏角(ɑ)和测点距(i)三者之间的几何关系,并结合现场进行检验,在金温货线武义站、芝溪站曲线维修中实际应用,取得较好的效果。
1 曲线正矢总和的计算
1.1 曲线正矢总和公式
弦上任一点到曲线上的垂直距离叫做矢距,在中央点的矢距叫做正矢。如图1所示。
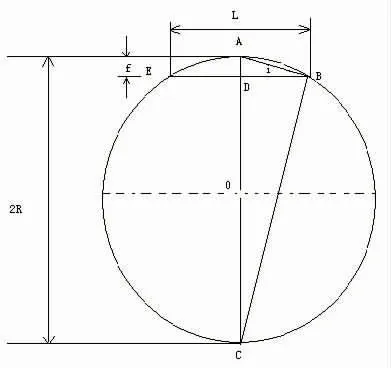
图1 正矢、半径、测点示意图
由于f与2R相比较,其值甚微,在(2R-f)项中,f可忽略不计,上式可近似地写成:
BD2=AD×DC AB2=AD×AC 即:

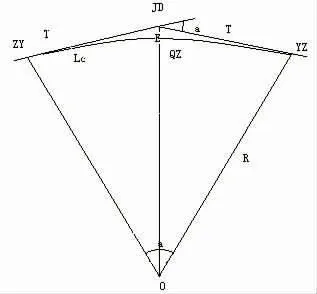
图2 曲线全长与偏角、半径关系示意图
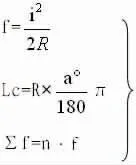

1.2 曲线正矢总和与其它参数的关系
由公式(1)可得,曲线正矢总和与曲线半径、曲线全长无关,与测点距、偏角成正比关系。
2 曲线正矢总和计算与应用
2.1 道岔岔后曲线正矢总和计算
(1)道岔岔后曲线正矢计算公式
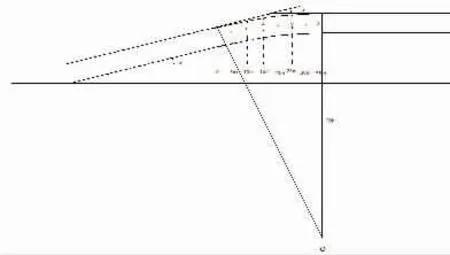
图3 岔后连接曲线示意图
如图3所示,道岔岔后连接曲线(特别是附带曲线)正矢点一般按5 m设置,按公式(1)计算Σf=8.7266×5a°=43.633a°
(2)12号道岔岔后连接曲线正矢总和计算
12号道岔(N=ctga=12)岔后连接曲线偏角为4°45'49'',转换为角度为4.763611°
Σf=8.7266×5a°=43.633a°=43.633×4.763611=207.85 mm≈208 mm
(3)9号道岔岔后连接曲线正矢总和计算
9号道岔(N=ctga=9)岔后连接曲线偏角为6°20'25'',转换为角度为6.34°
Σf=8.7266×5a°=43.633a°=43.633×6.34=276.6 mm≈277 mm
2.2 道岔岔后连接曲线正矢总和应用
(1)检验连接曲线正矢设置情况
根据上述公式可知,12号道岔岔后连接曲线正矢总和为208 mm。依此检验现场曲线整体方向,武义站1道3#岔后连接曲线偏角为4°45'49'',8个测点,实量第1点14,第2~7点30,第8点6,现场正矢总和为200 mm,比理论正矢总和少8 mm,现场实测正矢总和为203 mm;9号道岔岔后连接曲线正矢总和为277 mm武义站4道5#岔后连接曲线偏角为6°20'25'',8个测点,实量第1点23,第2~7点43,第8点11,现场正矢总和为292 mm,比理论正矢总和多15 mm,现场实测正矢总和为281 mm。由此判定,这两条曲线计划正矢设置错误。芝溪站2#岔(12号道岔)曲股与4#岔(9号道岔)曲股相连,连接曲线偏角为1.5764°(6.34°-4°45'49''),6个测点,实量第1点9,第2~5点16,第6点4,现场正矢总和为77 mm,比理论正矢总和大9 mm,现场实测正矢总和为73 mm;由此判定,这三条曲线计划正矢设置错误。
(2)正矢设置错误的原因分析
现场曲线头尾方向不良,曲线一端或两端有部分正矢“逃到”直线上,致使曲线正矢合计偏小;曲线两端夹直线存在“反弯”,直线部分存在反向曲线,造成曲线正矢合计偏大。计算曲线计划正矢时,现场正矢调查不细,造成现场正矢总和与计划正矢总和相差较大。按照三无曲线计算后存在计划正矢过大或过小的情况,曲线头尾点正矢计算错误等问题。由于计划正矢错误,导致曲线方向得不到有效整治,不利于列车运行平稳,甚至产生晃车。
检查或判断曲线正矢设置前,应核对曲线转角,通过曲线正矢总和及转角的几何关系计算出计划正矢总和,并与现场正矢总和大小比较,判断曲线正矢设置是否正确的一种有效方法。
3 三无曲线偏角计算
测点为5 m,测得温州西货场某三无曲线正矢分别为15 mm,19 mm,24 mm,23 mm,23 mm,31 mm,19 mm,27 mm,23 mm,29 mm,24 mm,35 mm,29 mm,25 mm,13 mm,计算正矢总和Σf=359 mm,该曲线偏角计算,根据公式(2)可得
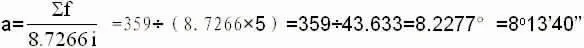
4 结束语
通过上述计算可知,掌握了正矢总和、偏角、测点距之间的几何关系,使曲线正矢理论计算更加便捷,为铁路曲线维养提供一个具有有实用价值的公式,也为曲线要素计算提供了一套值得参考的方法。
