基于TMD 原理的层间隔震结构的抗震性能分析
2020-11-05张玉涵杨德健师乐萌
张玉涵,杨德健,师乐萌
(天津城建大学 土木工程学院,天津300384)
近些年,高层建筑开始采用层间隔震技术,相关理论也不断完善.学者Chey 提出了在基础隔震的基础上结合层间隔震,以便使结构的稳定性得到更好的控制[1-2];Charmpis 以及Zhou 通过在多层建筑的不同位置设置隔震装置,将多种方案进行数值模拟分析,找出抗震效果最佳的方案[3-4];祁皑等表明在一定频率比范围内,当隔震层的位置较高时,其结构的上部加速度及下部位移都明显减小,工作机理类似于TMD[5];学者冯玲玲将层间隔震与TMD系统结合起来,建立混合控制模型,分析结果显示,混合结构在超出设防烈度的地震下有明显的减震效果[6]. 由此可见,国内外学者对层间隔震应用和原理的研究已取得了一些成果,但是对于将TMD 原理和层间隔震结构相结合的研究还需要更为具体的探索.
本文针对一框架-核心筒结构的办公大楼,依据TMD 原理在结构顶部设置隔震层,并确定隔震支座的参数与布置.将隔震层的上部结构看做TMD 质量块,下部结构作为TMD 减震系统的主体结构.通过Etabs分析不同情况下的地震响应规律,以此研究基于TMD原理的层间隔震结构对震动控制的有效性.
1 工程概况
工程实例背景为银川市一栋框架-核心筒结构的办公大楼. 该建筑分为地上18 层和地下1 层,建筑总高度65.1 m,一层和三层层高为5.1 m,二层层高为6 m,四层以上层高为3.6 m.地上三层为大底盘结构,上部结构规则对称.本结构抗震设防烈度为8 度,地震动峰值加速度为0.2 g.场地类别属于二类场地,设计地震分组属于第二组,特征周期近似于0.4 s.结构模型如图1 所示.
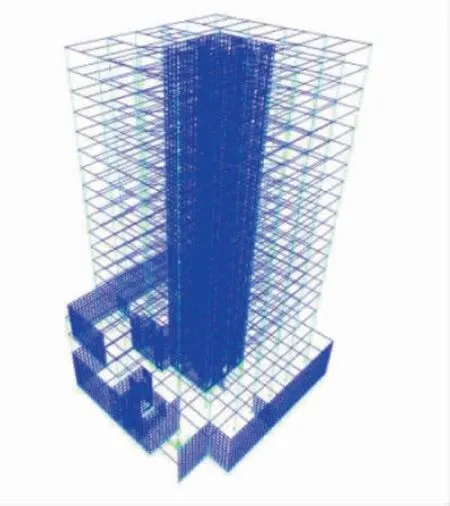
图1 结构模型
2 结构模型的设计与参数设置
2.1 TMD 减震系统理论基础
对于TMD 减震系统主要影响参数的分析,可将隔震层以上的结构简化为一个单质点,隔震层以下简化为另一个单质点[7],整个结构简化为双质点体系近似模拟其力学特性[8],则TMD 结构系统的隔震层布置示意如图2 所示,计算模型如图3 所示.
其运动方程为
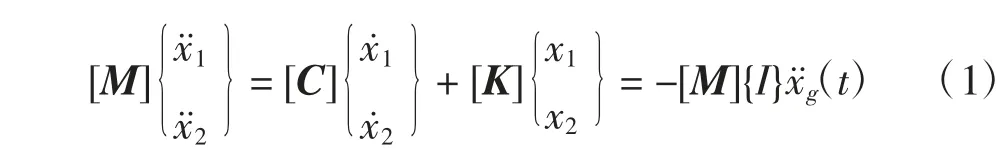
定义结构的上部与下部的重力荷载比γg和周期比γT为
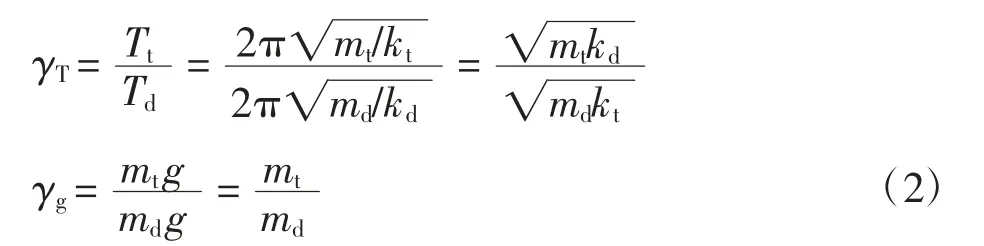
式中:mt,kt为上部结构(TMD 质量块)的质量与刚度;md,kd为下部结构(主体结构)的质量与刚度.
文献[9]通过模态分析和反应谱分析并经过多种工况的对比,得出上部结构与下部结构的最佳周期比应在0.8~1.8 之间,最佳重力荷载比在0.05~0.35 之间. 因此,在进行TMD 减震设计时,应将结构的上部与下部的重力荷载比和周期比作为重要的考虑因素.
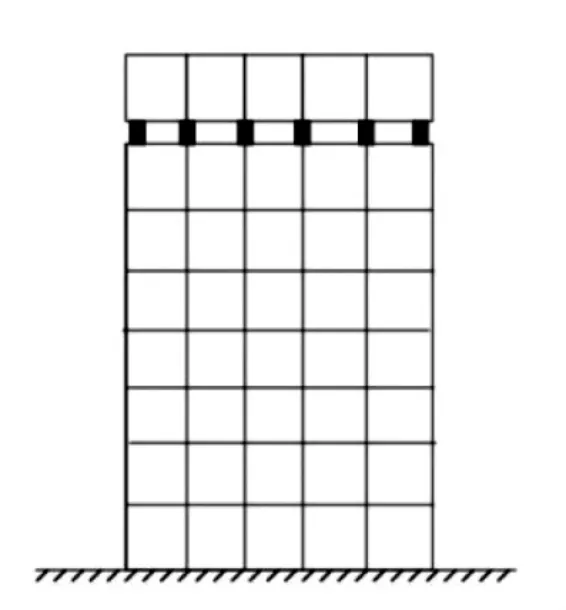
图2 隔震层布置示意
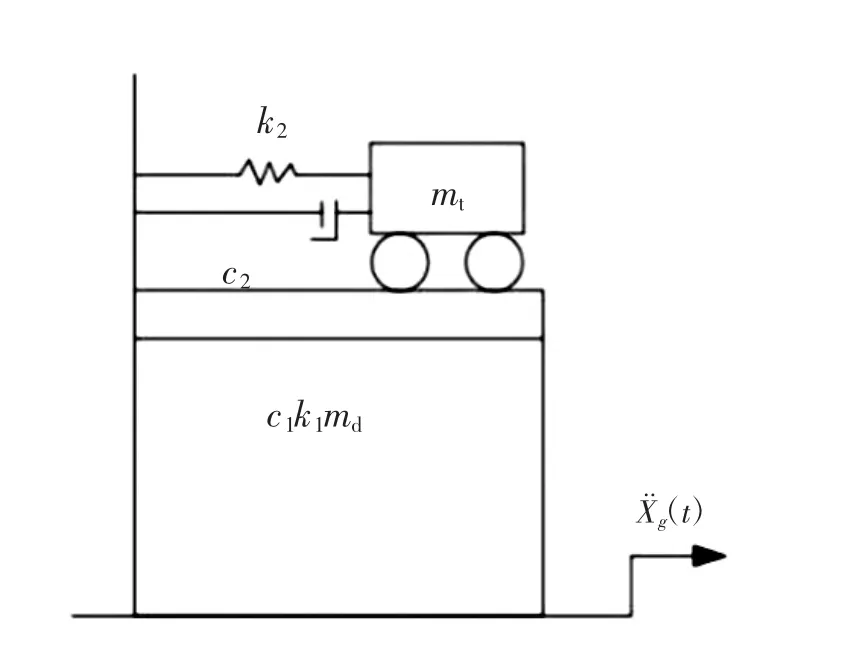
图3 TMD 结构系统计算模型
2.2 TMD 减震系统参数设置
结构的总质量为m=42 705 t,结构的基本自振周期和自振频率分别为T=1.594 s、f=3.94 Hz. 设TMD的质量块(即上部结构)的质量为mt,主体结构(即下部结构)的质量为md,综合考虑各项因素,初步选择结构顶部两层作为TMD 质量块.
TMD 质量块质量为mt=3 494 t;TMD 刚度为kt=mtf2= 3 494 × 3.942= 54 239 kN/m;TMD 阻尼为ct=2ζmtf=2 × 0.05 × 3 494 × 3.94 = 1 376.64 kN·s/m;主体结构的质量为md=39 211 t;主体结构的刚度为kd=mdf2=39 211×3.942=608 696 kN/m.将以上数据带入公式(2)可得:γg=1;γT=0.09.
由前文可知,当上部结构与下部结构的周期比在0.8~1.8 之间,重力荷载比在0.05~0.35 之间时,层间隔震的隔震效果最佳. 经计算,选择结构顶部两层作为TMD 质量块为理想方案.
2.3 隔震支座参数设置与布置
取顶部两层为隔震层上部结构,依据TMD 刚度近似等于隔震层水平刚度的原则,选取型号分别为LRB500-100、LRB400-80、LRB350-60 的铅芯叠层橡胶隔震支座共28 个.相关产品参数与数量见表1.隔震层平面布置如图4 所示.
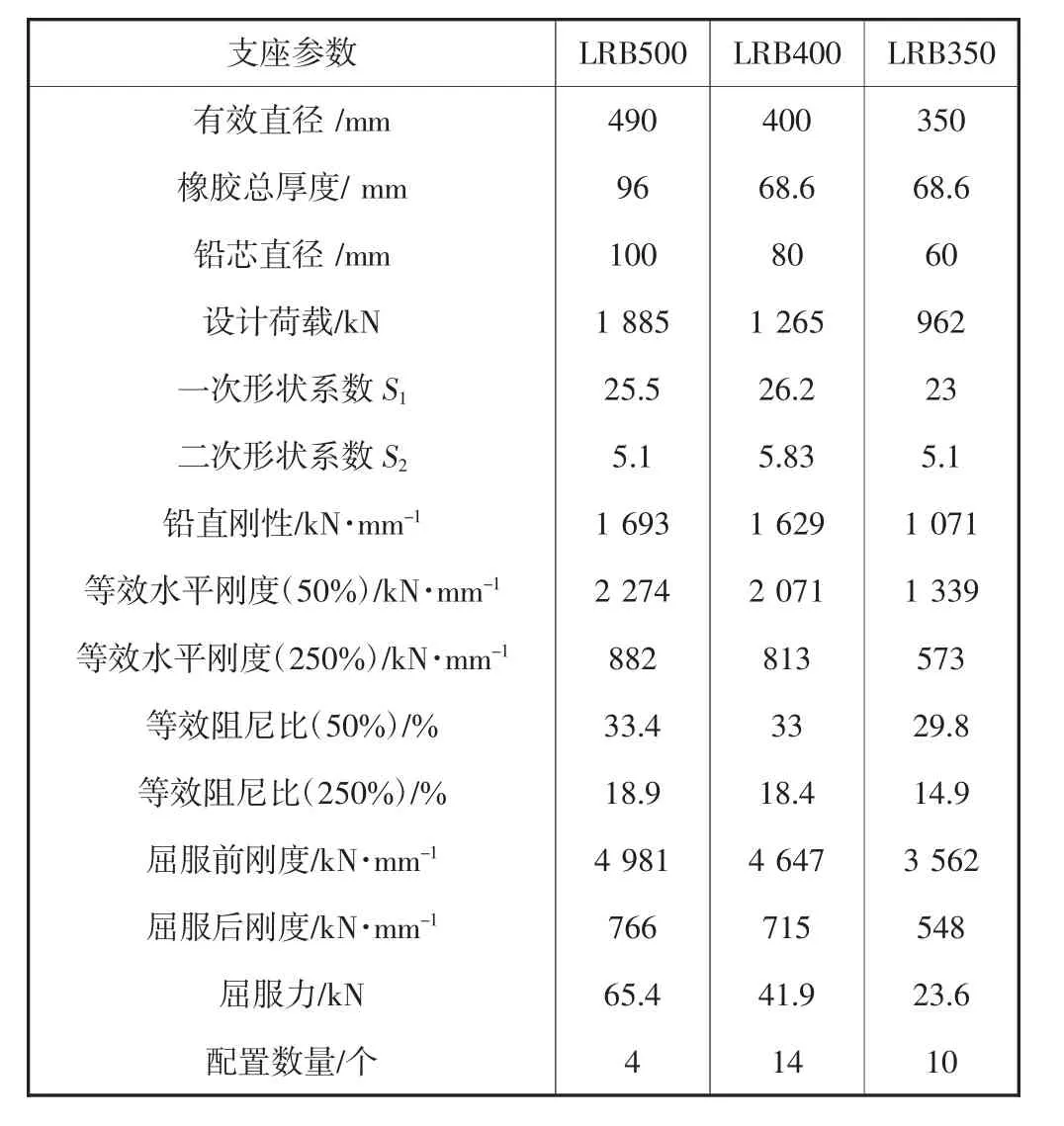
表1 隔震支座的参数指标
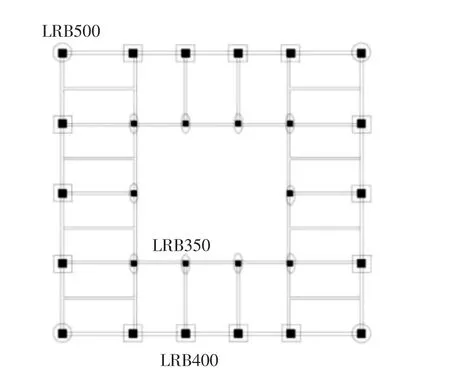
图4 隔震层平面布置
2.4 输入地震波的选取
依据(GB50011—2010)《建筑抗震设计规范》[10]选择El-Centro 波、Tar-Tarzana 波和唐山波这三条波进行动力时程分析[11-12].三条波基本参数见表2;经过调幅之后的各地震波时程曲线见图5.
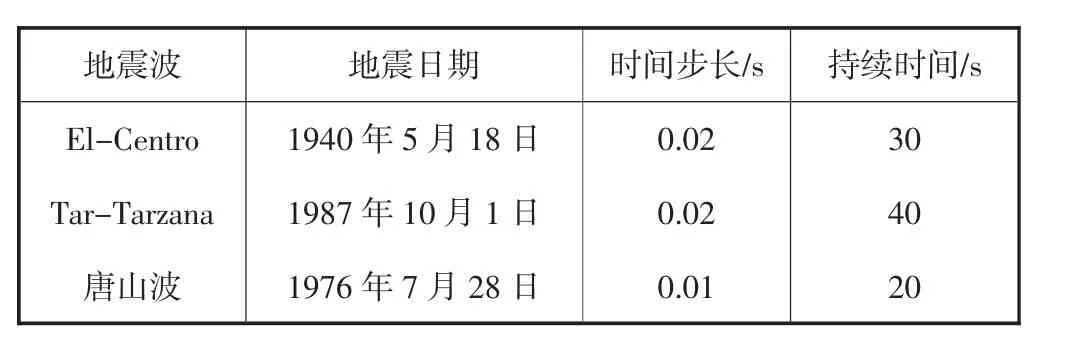
表2 地震波基本参数
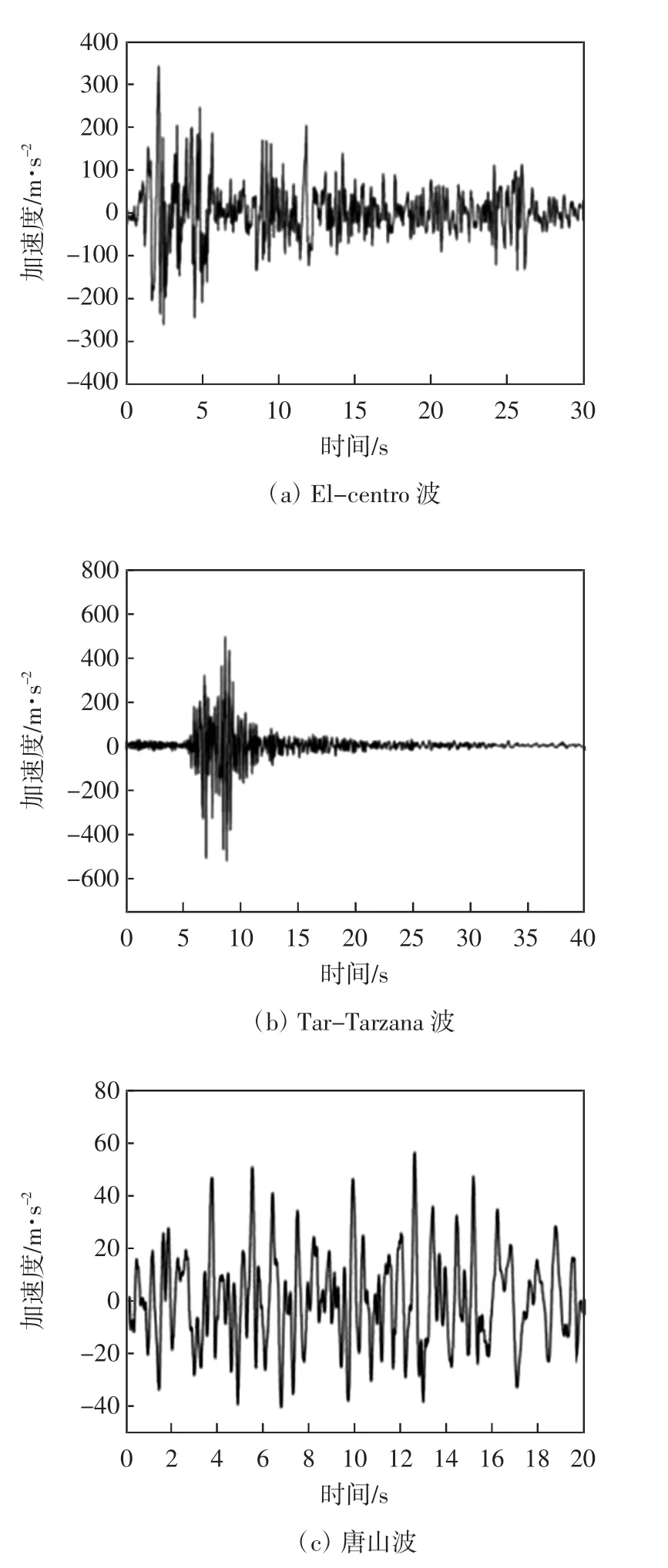
图5 三条地震波时程曲线
3 结构地震反应分析
3.1 结构的模态分析对比
利用有限元分析软件,求解传统非隔震结构与隔震结构的振型,得出结构的自振特征和振型质量参与系数.表3、表4 分别为传统非隔震结构与隔震结构的前5 阶振型周期与质量参与系数的数据.
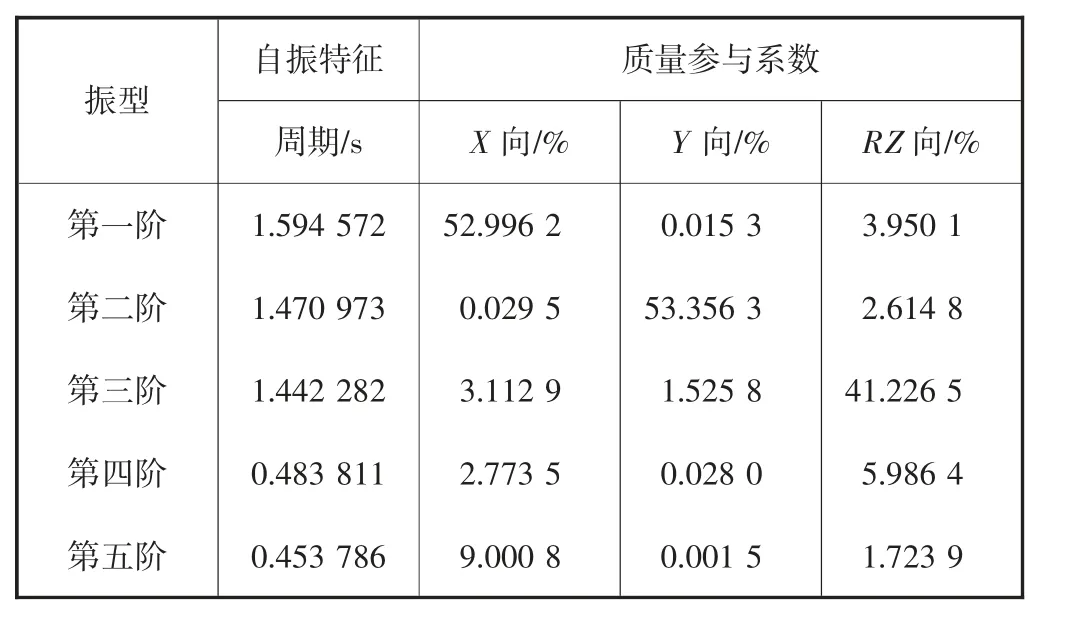
表3 传统非隔震结构前10 阶自振周期与质量参与系数
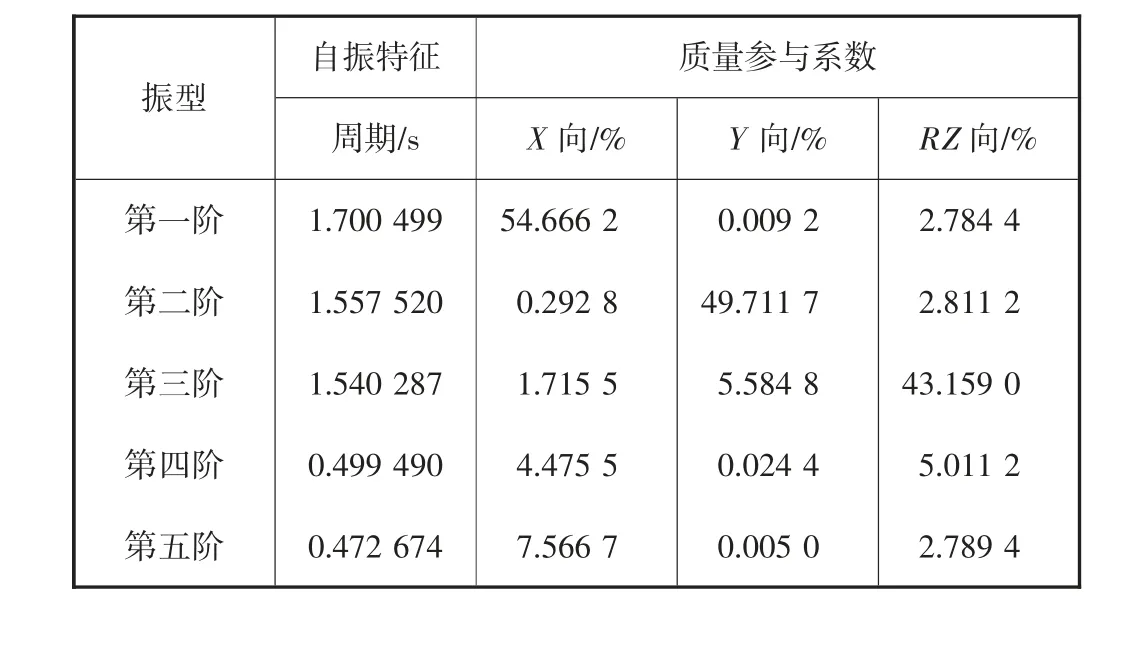
表4 隔震结构前10 阶自振周期与质量参与系数
通过表3、表4 可知,传统非隔震结构基本周期为1.595 s,隔震结构基本周期为1.70 s,顶部隔震结构较传统非隔震结构的自振周期得到了延长.对于传统非隔震结构和隔震结构,可以看到第一振型X 方向的质量参与系数远大于Y 方向与RZ 方向的参与系数,所以两种结构第一振型都以平动为主.同理,第二阶振型是以Y 方向的平动为主,第三阶振型以扭转为主.
3.2 多遇地震作用下结构动力时程分析
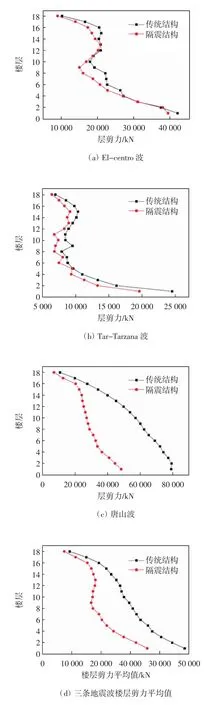
图6 三条地震波下两种结构楼层剪力对比
图6 给出了传统非隔震结构与隔震结构在多遇地震作用下的层间剪力最大值对比.由图6 可知:结构楼层剪力从上到下依次增大,在El-centro 波下15至18 层和5 至9 层比其他楼层层间剪力有明显的减小.在Tar-Tarzana 波下隔震建筑的中部主体结构的减震效果明显,尤其是第9 层,层间剪力由传统非隔震结构的9 555 kN 降至隔震结构的7 014 kN.对于唐山波而言,隔震建筑不论是上部结构还是主体结构,都得到了较大幅度的减小,其中最明显的为8 层,层间剪力由传统非隔震结构的28 623 kN 降至隔震结构的15 620 kN,层间剪力减小率达54%.这说明隔震结构充分发挥了对主体结构的减震效能,减缓了主体结构的地震响应.
图7 给出了三种地震波下顶层加速度的对比.由图7 可以看出,在三种地震波下,隔震结构顶层加速度均有所下降,减震率分别为74%、67%、79%,这充分说明层间隔震对上部结构起到了良好的隔震效果.
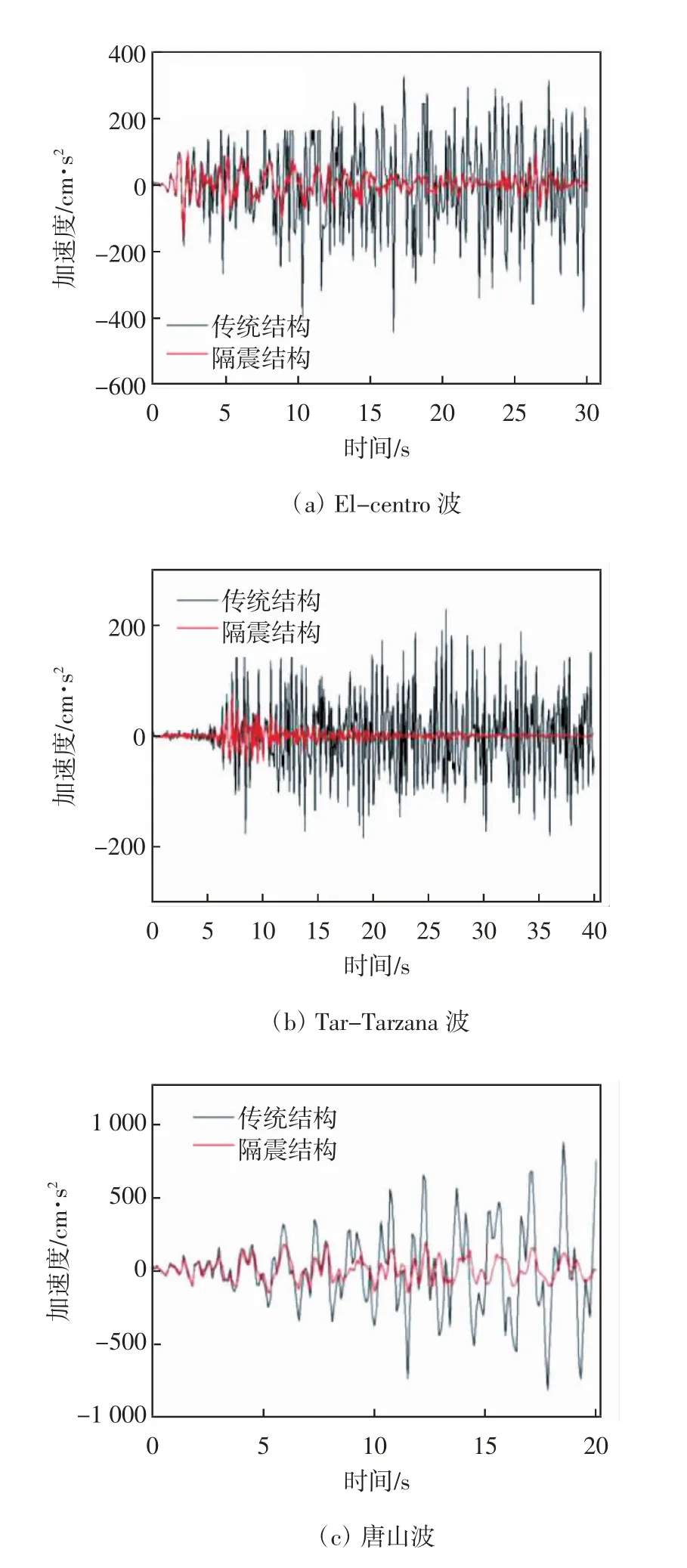
图7 三种地震波下顶层加速度的对比
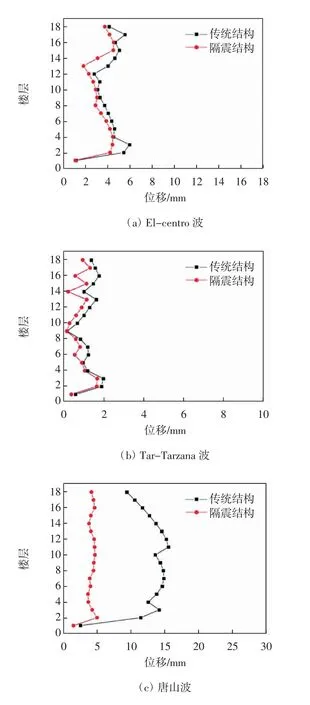
图8 不同地震波下两种结构X 向最大层间位移值
图8 给出了不同地震波下两种结构X 向最大层间位移值.由文献[10]可知:各类结构应进行多遇地震作用下的抗震变形验算,其楼层内最大的弹性层间位移角应满足小于1/800 的限制要求.由图8 可知,在多遇地震情况下,三种不同地震波作用下的结构的最大层间位移值都满足弹性层间位移角小于1/800 这个限制(即层高为3.6 m 时最大层间位移不超过4.5 mm;层高为5.1 m 时最大层间位移不超过6.4 mm;层高为6 m时最大层间位移不超过7.5 mm).特别是在唐山波作用下,传统非隔震结构的每一层都超过了最大层间位移角的限制,其中传统非隔震结构X 向最大层间位移为15 mm.但是其加装隔振系统后都符合限值要求且满足规范,这为了表明隔震结构能使层间位移明显减小,隔震效果十分显著.
3.3 罕遇地震作用下结构动力时程分析
由文献[10]可知,隔震建筑应进行罕遇地震作用下的时程分析,且橡胶隔震支座的拉应力应小于1 MPa(即LRB500 型隔震支座受拉小于196.25 kN).一般隔震结构的角部会率先出现受拉的情况,所以提取了角部隔震支座LRB500 的最大拉应力.使用选择的三条地震波,考虑X、Y、Z 三向比例为1 ∶0.85 ∶0.65的罕遇地震激励,得出隔震支座在三条地震波的作用下最大拉力值,根据计算,均满足规范规定,故本文所用隔震结构满足罕遇地震下的规范要求.
图9 给出了三条地震波下两种结构楼层剪力对比.图10 给出了罕遇顶层加速度时程曲线对比.由图9 可知,在罕遇地震作用下,相比较于传统非隔震结构,隔震建筑上部的层剪力和主体的层剪力都得到了一定程度的减小,其中隔震层以下的结构减震效果最明显,最高地震减小率已经达到了45%. 说明结构很好地结合了TMD 减震原理,使得主体结构的层间剪力得到了有效减小. 由图10 可知,罕遇地震下隔震结构的顶层加速度也比传统非隔震结构的加速度有大幅度的减小. 尤其是上部结构加速度响应减小更为明显. 说明隔震支座充分发挥了其对上部结构隔震的性能,在罕遇地震下也取得了不错的减震效果.
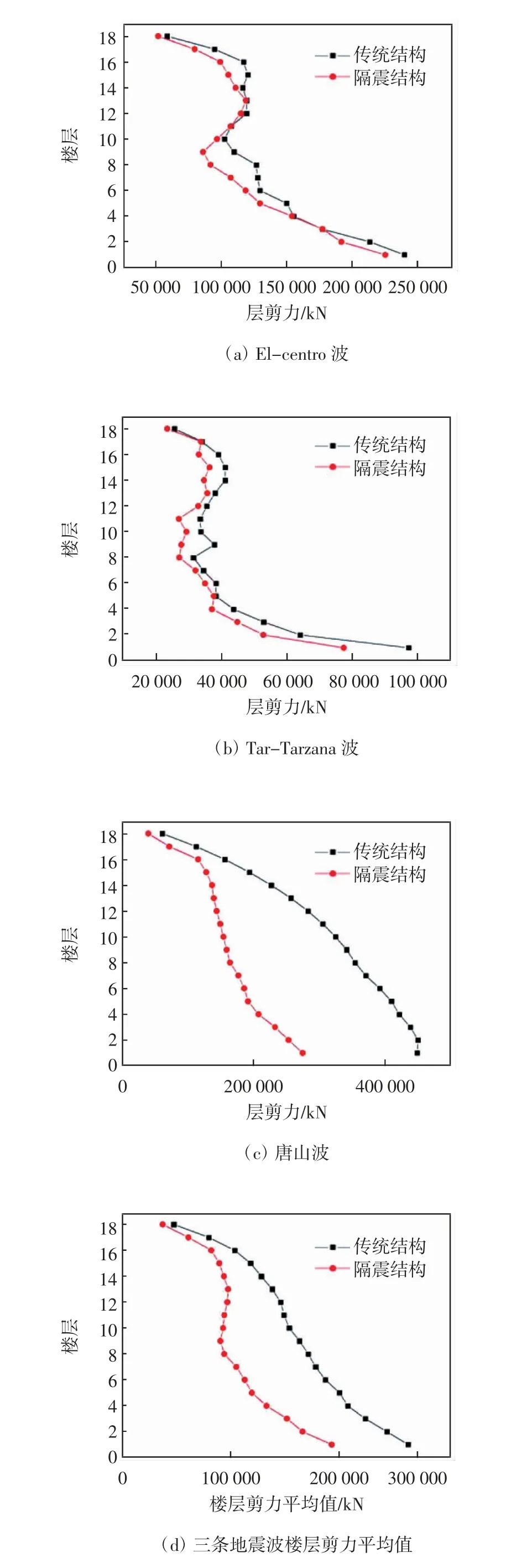
图9 三条地震波下两种结构楼层剪力对比
图11 给出了不同地震波下两种结构X 向最大层间位移值.由文献[10]可知:罕遇地震下框架核心筒结构进入弹塑性阶段时的层间位移角应小于1/100(即层高为3.6 m 时最大层间位移不超过36 mm;层高为5.1 m 时最大层间位移不超过51 mm;层高为6 m 时最大层间位移不超过60 mm). 从图11 中可以看出El-centro 波和Tar-Tarzana 波不论是传统非隔震结构还是隔震结构,都符合其限制要求,不会出现弹塑性破坏.唐山波由于震害比较大,传统非隔震结构基本都超出了弹塑性层间位移角限值的要求,但隔震结构的层间位移角值都在规范要求范围内,不会发生塑性破坏.并且在唐山波作用下的隔震结构的主体结构和上部结构的层间位移角基本都小于弹性层间位移角限值1/800(即层高为3.6 m 时最大层间位移不超过4.5 mm,层高为5.1 m 时最大层间位移不超过6.4 mm;层高为6 m 时最大层间位移不超过7.5 mm),所以结构整体基本处于弹性阶段.对于罕遇地震下El-centro波和Tar-Tarzana 波,隔震结构都超过了弹性范围,但是进入塑性状态程度不深.
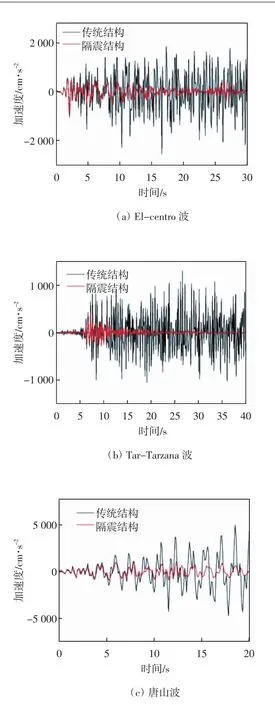
图10 罕遇顶层加速度时程曲线对比
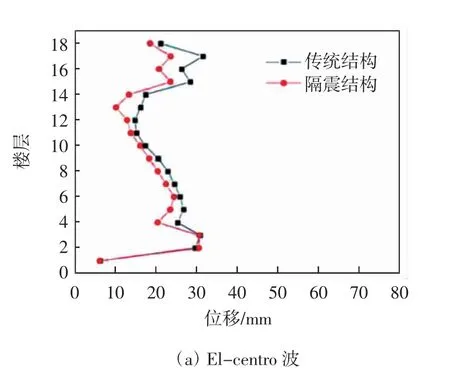
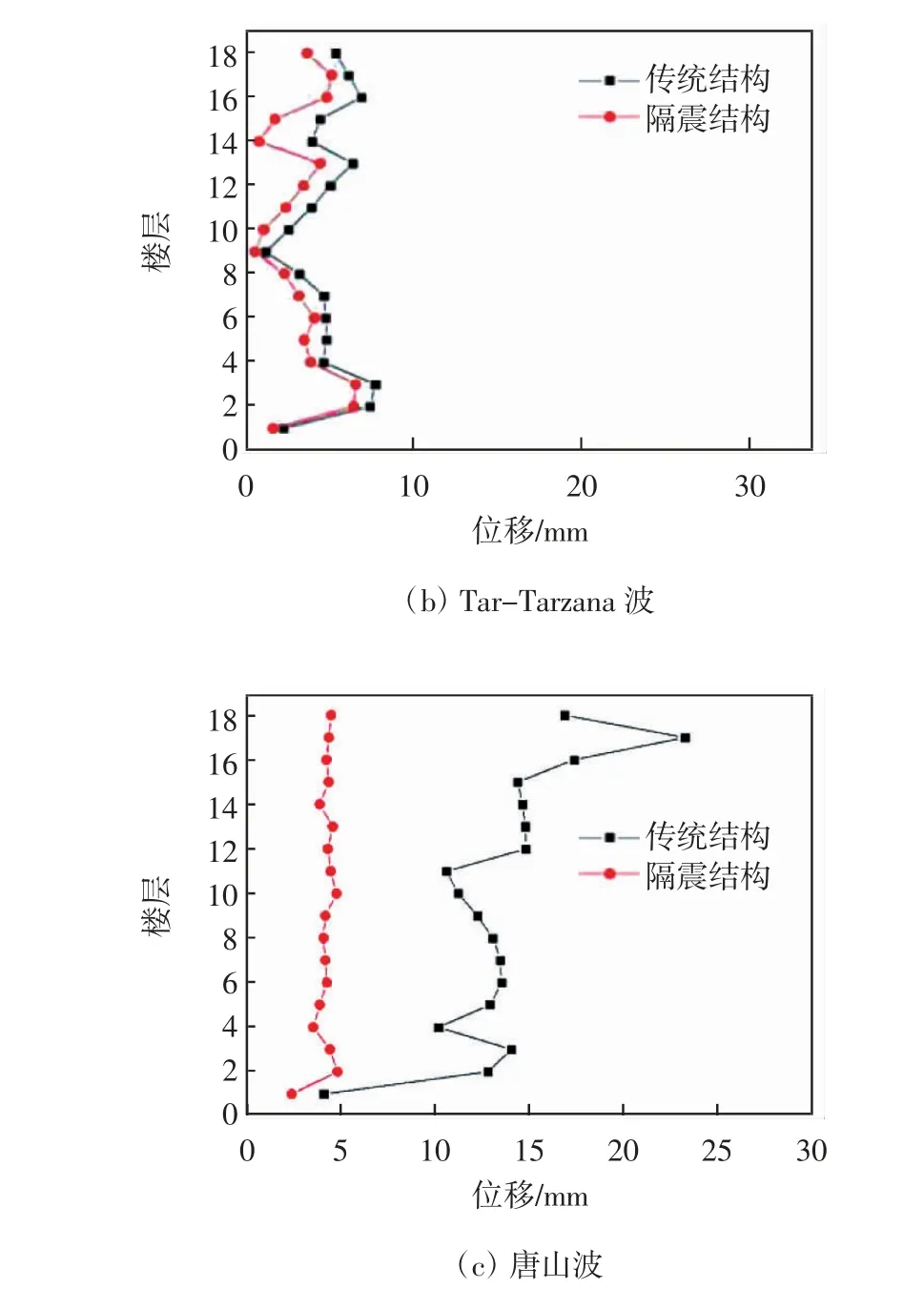
图11 不同地震波下两种结构X 向最大层间位移值
4 结 论
通过对框架-核心筒结构的隔震设计与建模,以及在多遇地震和罕遇地震作用下进行的动力时程分析,将传统非隔震结构与顶部采用基于TMD 原理的层间隔震结构进行对比,得出以下结论.
(1)基于TMD 原理设计的隔震结构在不同地震波下的减震效果有所不用,但相较于传统非隔震结构总体都有不错的减震表现.
(2)在多遇地震下,利用TMD 原理设计的层间隔震结构的隔震层不仅可以减少地震能量的上传,使顶部平均减震率达73%,还能有效地利用TMD 原理控制隔震层下主体结构的地震响应.
(3)在罕遇地震作用下基于TMD 原理设计的隔震结构可以很好地控制上部结构和主体结构的位移和变形.其中,主体最大层间减震率可达45%,并且使建筑达到罕遇地震下基本不出现塑性破坏的要求.
