直槽沟埋式管道的垂直土压力计算模型
2020-11-05安宗文王莹莹张永明
安宗文, 王莹莹, 张永明
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
目前,管道运输己与铁路、公路、航空、水运一起构成了中国五大运输行业体系[1],可以说管道输送是石油及天然气运输的主要支柱[2].但是,管道属于隐蔽工程,观察和检修都较为困难,发现问题时往往已经造成严重损失[3].随着PE管的广泛应用,作为沟埋式管道中主要结构件之一的钢塑转换结构件,其应用越来越广泛.钢塑转换结构件的可靠性和安全性将直接影响整体管道的使用性能.该结构在受到土载荷的作用下,PE 管易发生变形而导致该结构件失效,进而导致管道发生泄漏造成危害[4-5].根据相关文献[6]可知,在土载荷中,垂直土压力是该结构件承受的主要荷载.因此,准确计算埋地管道的垂直土压力数值变得尤为重要.
20世纪初,美国土木工程专家马斯顿论文中首次提出了计算埋管土荷载的理论及方法,并作为研究管道土压力的理论基础一直沿用至今[7].为了完善该模型,许多学者相继提出了多种计算管涵土压力的理论与方法[8].现有的垂直土压力理论大致分为五类:散体极限平衡法、土柱法、土压力集中系数法、卸荷拱法和弹性力学法.尽管在过去几十年中相继提出了多种计算管涵土压力的理论与方法,但马斯顿理论依然在管道设计中被广泛采用.
然而,马斯顿理论没有区分刚性管道和柔性管道,忽略了主应力对土体屈服、破坏的影响和随着埋深的增加,管道两侧回填土对垂直土压力的影响.马斯顿认为,管道承受了槽内回填土的所有荷载.据实验研究,管道两侧回填土对承担上部土柱载荷是有贡献的.因此,马斯顿理论的计算值无法准确地反映垂直土压力作用于钢塑转换结构件上的实际强度[9-10].埋地管道示意图如图1所示.
综上所述,本文在假设沟埋式管道为柔性管的前提下,考虑主应力σ2和随着埋深的增加,管道两侧回填土对垂直土压力的影响,利用直槽沟埋式燃气管道垂直土压力的直线滑裂面计算模型和双剪统一强度理论,推导并建立了垂直土压力计算模型,并利用有限元软件进行模型的对比验证.本文所建的模型可为直槽沟埋式管道的垂直土压力计算提供一种新方法.
1 管道分类
在文献[11]中规定划分刚性管与柔性管的方法如下:
(1)
式中:Ep为管道材料的弹性模量,MPa;Ed为管侧回填土的变形综合模量,MPa;ε为管壁厚度,mm;ro为管心到管壁中线的距离,mm.
通过计算,聚乙烯(PE)管道属于柔性管的范畴.对于柔性管,由于其自身刚度较小,在上部土压力作用下,竖直向和水平向的变位都比较大[12],导致管道两侧的回填土去承担上部土体的部分荷载.因此,本文结合双剪统一强度理论和直槽沟埋式燃气管道垂直土压力的直线滑裂面计算模型,建立了一种适用于刚、柔性管道的垂直土压力计算模型.
2 双剪统一强度理论
俞茂宏教授对强度理论问题进行了系统及深入的研究,提出了可以考虑主应力σ2影响的双剪强度理论[13-14].其研究对象是双剪单元体,定义为:当作用于单元体上的最大剪应力和中间剪应力的函数达到某一极限值时,材料开始屈服.
双剪统一强度理论主应力表达式为
(2)
(3)

在此引入Lode参数,取:
(4)
将式(4)和式(2,3)进行比较,可得
当μσ≤sinφo时,式(2)可以写成:
(5)
当μσ>sinφo时,式(3)可以写成:
(6)
式中:co为土体的内聚力.
令
(7)
式中:ct为材料的统一黏聚力;φt为统一内摩擦角.
则μσ≤sinφo时:
μσ>sinφo时:
(10)
(11)
φt和ct随主应力σ2的变化呈现出区间性,极值点所对应的μσ=sinφo.
则式(7)可写为
(12)
根据一点应力状态的摩尔圆,研究与主应力作用面即水平面成θ角的面,其面上作用法向应力σ和剪应力τ[15].即
式(14)同时也是平面应变问题,当土中一点达到极限平衡状态时,该点的大、小主应力应满足极限平衡条件.

cos 2θ=-sinφt
(17)
因此
(18)
将式(18)带入式(15,16)后可得
联立式(14~16,21)可转化为
(21)
(22)
(23)
从式(21)可以看出,剪应力τ的分布特征随着主应力σ1及材料的参数φt和ct取值变化而变化.该数学表达式为推导垂直土压力计算模型奠定了理论基础.
3 垂直土压力计算模型
3.1 直线滑裂面模型
对于直槽沟埋式埋地管道,管道和基础的变形使得槽内填土达到极限应力状态(管道填土以管道宽度为基础),形成一个下滑的土柱体,其滑裂面为与水平面成β角的斜面.
一要更好促进短期绩效与长期发展之间的综合平衡。农业产业扶贫资金多是在财政体制常规分配渠道之外,按照专项资金和项目制方式进行资源配置。农业生产的周期性特征决定了农业产业发展的特殊性,往往需要三五年甚至更长时间的持续投入,才能形成比较成熟的产业链。当前,个别贫困地区在产业扶贫项目资金的投入使用上,更偏向于追求财政绩效考核意义上的短、平、快,希望收到立竿见影的效果,这容易导致产业扶贫出现重短期效应、轻长效机制、组织化程度低、同质化严重等问题。解决这些问题,必须有“功成不必在我”的精神境界和“功成必定有我”的责任担当,真正以长远眼光,厚植产业发展的长久根基。
如图2所示,斜面AO与斜面LM即为所形成的斜向滑裂面.Ⅰ区、Ⅱ区滑裂面的高度分别为[10,16-18]
3.2 土体压力计算
根据上述的分析,由于存在Ⅰ区和Ⅱ区两个分区,因此对其进行受力分析,如图3所示.
3.2.1Ⅰ区土体作用
在填土下面z深处(0≤z≤h1)取厚度为dz的土层为分离体,Ⅰ区受力情况如图3a所示.
竖向静力平衡公式为
γBdz-Bdσz-2τdz=0
(26)
经过计算,可以得到Ⅰ区的竖向土压应力[14]:
(27)

3.2.2Ⅱ区土体作用
在填土面下z深度处(h1≤z≤H) ,即Ⅱ区取厚度为dz的土层为分离体,其受力情况如图3b所示.
竖向静力平衡条件为
(28)
横向静力平衡条件为
(29)
由图2可知:
(30)
联立式(28)和式(29)可转化为
(31)
解得
(32)
当取Ⅰ区与Ⅱ区土体的临界处时,即z=h1,则
(33)
将其作为边界条件,带入式(32),则求得常数项为
(34)
将式(34)带入式(32)可得
(35)
当z=H时:
(36)
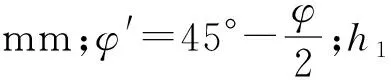
至此,直槽沟式管道的垂直土压力计算模型建立完毕.
4 算例分析
本文以城市燃气管网中所用的带有燃气管网用钢塑转换结构件的埋地管道为验证对象,对本文推导并建立的直槽沟埋式的垂直土压力计算模型的有效性和合理性进行分析和验证.本算例中,验证对象的具体结构参数及相关物理参数见表1.表1的相关说明:

表1 验证对象的几何参数和物理参数Tab.1 Geometric and physical parameters for an example to validate
1)D1为燃气管网用钢塑转换结构件的钢制组件的直径;D2为燃气管网用钢塑转换结构件的PE管道的直径;D3为燃气管网用钢塑转换结构件的压紧件的直径;
2) 采用沟埋式敷设方式,回填土为黏性土,进行分层压实;
3) 在计算时取管径D2=200 mm进行计算,对于钢塑转换结构件,易出现失效的部分为PE管端.根据文献[11]的研究成果,取b=0.5.
由表2可知,随着槽宽的增大,管顶土压力随之减小.主要原因是:随着槽宽的增大,直线滑裂面也随之增大,滑裂面处产生的支撑力也增大.
同样由表2可知,随着覆土厚度的增大,管顶土压力随之增大.在覆土厚度达到3.5 m后,管顶土压力几乎不变.

表2 不同覆土厚度和槽宽下的管顶土压力Tab.2 Soil vertical pressure under different thicknesses of covered soil and widths of groove kPa
根据GB 50028—2006城镇燃气设计规范要求,对于单管敷设的埋地管网,其沟底宽度为D+0.3 m.当B=0.5 m时,管顶土压力在不同覆土厚度下的传统土压力与本文土压力计算值见表3.

表3 不同覆土厚度下的传统土压力与本文土压力的管顶土压力计算值Tab.3 As-calculated values of soil vertical pressure and those determined in this paper in the case of different thicknesses of covered soil
由表3可得到以下结果:
1) 本文建立的垂直土压力模型与马斯顿模型的计算结果趋势相同;
2) 本文建立的垂直土压力模型的计算值与马斯顿模型的计算值相差约40%;
3) 覆土深度达到4 m后,垂直土压力的数值不再随着覆土深度的增加而有所变化,因此本文建立的垂直土压力模型的适用范围为4 m以内,满足城市燃气管网的使用要求.
5 有限元分析
为了进一步验证上述结论,利用ANSYS有限元软件进行分析.首先,根据上述计算得到的理论值进行管道的仿真压力试验,得到管道的应力值Ⅰ;然后,根据管道与土体间的相互作用关系,建立埋地管道的有限元模型,得到管道应力值Ⅱ.最后将两种应力值进行比较,验证模型的可行性.
模型中PE管的直径D2=200 mm,壁厚δ=18.2 mm,PE管的弹性模量Ep=1 070 MPa,泊松比μ=0.38.在不考虑管道自重的条件下,假设管周土质均匀,土体容重为18 kN/m3,回填土的土变形模量Eo=8 MPa,泊松比μ=0.35.
对于仿真压力试验,由于试件长度为100 mm,管端的长度与直径相差很小,在仿真模拟试验中必须考虑端面效应,必须建立三维模型,如图4所示.在对材料参数进行设定时,不考虑上下两块板的变形,因此将其设定为刚性体,其尺寸大小为200 mm×100 mm×3 mm,下表面的面积为20 000 mm2.
施加载荷和约束.根据仿真压力试验的分析,板四周的四个表面限制其x方向和z方向上的移动.在其中一块板的上表面施加载荷,载荷值的计算方法如下:
F=σz,HA
(37)
根据仿真压力试验得到最大接触压力,见表4.表中将利用马斯顿理论进行的仿真压力试验定义为仿真压力试验Ⅰ,利用本文所建模型进行的仿真压力试验定义为仿真压力试验Ⅱ.

表4 不同覆土厚度下埋地管道的应力Tab.4 Stress values of buried pipeline under different thicknesses of covered soil
由于埋地管道的长度无限,因此在建立埋地管道的有限元分析模型时将管道横截面上土压力的求解简化为平面应变问题.管道模型中两侧到管道中心的距离为3.5D(D为管道外径)、地基底部到管道中心的距离为4.5D,模型几何尺寸如图5所示.对模型进行网格划分,如图6所示.
建立埋地管道的有限元分析模型时,要考虑管道与土体间的相互作用关系,管道与土体之间存在压力传递的同时,还存在相互间的摩擦力和相对位移,管土之间的相互作用还存在非线性的特征.因此,在对管土之间的相互作用进行仿真模拟时需建立接触对.将管道与土体间的接触设定为面面接触,土体作为目标面,相应的管道作为接触面.
施加载荷和约束,土体的左右两侧限制其x方向上的移动,底部限制其y方向上的移动.同时施加重力G=9.8N.管土间的接触设置为柔性接触,管土相互间的摩擦系数为0.25.管顶覆土高度H的取值依次为1.0、1.6、2.0、2.4、2.8、3.2、3.6 m.仿真模拟得到的最大接触压力见表4.
由表4可知,本文建立的埋地管道有限元模型与仿真压力试验的结果相一致,进一步验证了本文所建理论模型的可行性.
6 结论
1) 本文考虑主应力对土体屈服与破坏的影响及随着埋深的增加,管道两侧回填土对垂直土压力的影响建立的垂直土压力模型.
2) 本文所建模型的计算结果相较于马斯顿理论的结果减小了40%.如果仍用马斯顿理论进行计算,在进行设计或强度校核时必然导致用材过度,因此应进行适度折算.
3) 本文得到的计算模型适用于刚性、柔性管道的垂直土压力计算.
4) 对于直槽沟埋式燃气管网用钢塑转换结构件,管道两侧回填土能够承担一部分土体荷载,而且随着槽宽的增大,此现象越明显且无法忽略.因此,在实际工作中选择合适的开槽宽度,尽量避免过度开挖.
5) 通过本文的建模分析过程和得到的计算模型,为直槽沟埋式管道的垂直土压力计算提供一种新方法.
