一种改进的多无人机覆盖航迹规划方法
2020-11-05张小孟胡永江李文广张世华庞强伟
张小孟,胡永江,李文广,张世华,庞强伟
(陆军工程大学石家庄校区 无人机工程系,石家庄 050003)
无人机以其造价低、体积小、零伤亡等优势被应用于现代战争的各个方面,如侦察监视[1]、通信中继[2]、精确打击[3]等,具有巨大的发展潜力和应用前景。在无人机作战运用中,多无人机区域覆盖侦察任务[4]主要是指在任务区域面积较大,区域内目标属性未知,又需要得到完整任务区域信息的背景下,对任务区域进行全覆盖侦察。在执行任务前首先要为各任务机规划飞行航迹,即多无人机区域覆盖航迹规划问题,规划的要求是根据任务区域大小、形状、无人机数量以及载荷性能,结合相应的航迹规划算法,规划得到各个任务机的飞行路径,使无人机可完全侦察覆盖任务区域,且满足飞行路径代价最小的指标要求。
现阶段国内外对于多无人机区域覆盖航迹规划问题的解决方法一般分为两步[5,10]:第1步根据无人机的数量和无人机的侦察能力等要素,对任务区域进行分解,得到等无人机数量的子区域。第2步在各个子区域内,规划相应任务机的飞行航迹。对任务区域的分解,文献[6]提出了一种基于任务性能和子区域宽度的任务区域分解算法,将凹多边形分解为多凸多边形,解决凹多边形的区域覆盖侦察问题。文献[7]提出一种区域分解方法,实现了三角形任务区域的快速分解,仅讨论了三角形任务区域的分解方法。文献[8]提出了一种以无人机飞行时间最短为目标的区域分解和分配算法,保证了整体侦察时间最短。但该方法仅适用于矩形任务区域,算法普适性弱。文献[9-10]根据无人机初始位置和各任务机的搜索面积要求对任务区域进行分解,但是分解算法比较复杂,分解效率低。
上述方法可以在某些方向上解决多无人机区域覆盖侦察航迹规划问题,但仍存在以下不足:① 分解时只是针对特定区域形状如矩形或者三角形,普适性比较差;② 分解方法比较复杂,分解效率低。
针对上述问题,本文提出了一种改进的多无人机覆盖航迹规划方法,可用于解决多无人机侦察凸多边形(凹多边形可以首先分解为多个凸多边形)区域内覆盖航迹规划问题,且该方法相对于现有的基于凸多边形分解的多无人机覆盖航迹规划方法具有代价低、效率高的特点。
1 任务模型
多无人机区域覆盖航迹规划问题可以描述为:给定任意有界封闭区域S和N架同构或异构无人机UAVn(n=1,2,…,N)。要求无人机携带侦察载荷,从地面站位置起飞,对封闭区域S进行覆盖侦察,后返回起飞点。要求设计一种航迹规划方法,可为各任务机规划相应的侦察航迹,实现N架无人机满足整体路径代价最小的情况下,对区域S完全覆盖侦察。
为了简化问题模型,作出以下合理假设:N架无人机为同构无人机且携带相同的侦察载荷。无人机在执行任务时,载荷镜头保持垂直向下。所有无人机从相同的地面站起飞,回到地面站。侦察覆盖区域是凸多边形任务区域(三角形、矩形均属于凸多边形)。
针对载荷镜头保持垂直向下的侦察模式,建立相应的载荷模型,如图1所示。无人机沿X方向飞行,H为无人机的飞行高度,O为载荷中心在地面上的垂直投影,矩形区域ABCD为无人机的探测区域,其中运动方向上的探测步长L,探测宽度W。
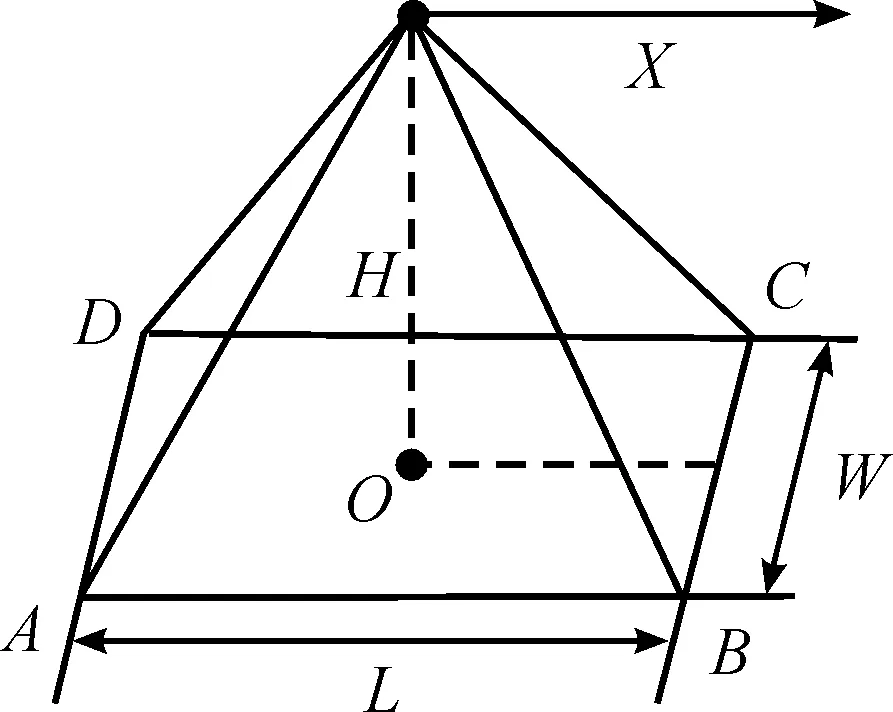
图1 载荷探测模型示意图
约束条件为:
1) 单架无人机无人机执行任务的能力约束,无人机携带能源有限,因此具有航程限制,在其载荷和飞行高度确定的情况下,无人机执行扫描任务具有最大限制:
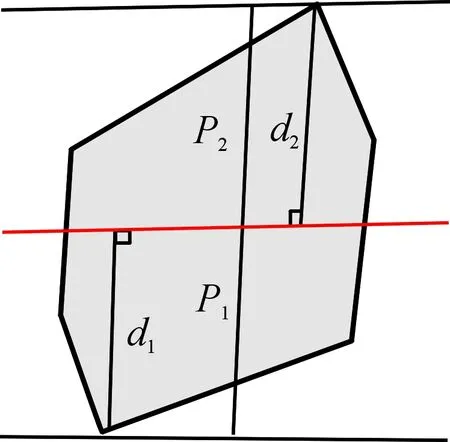
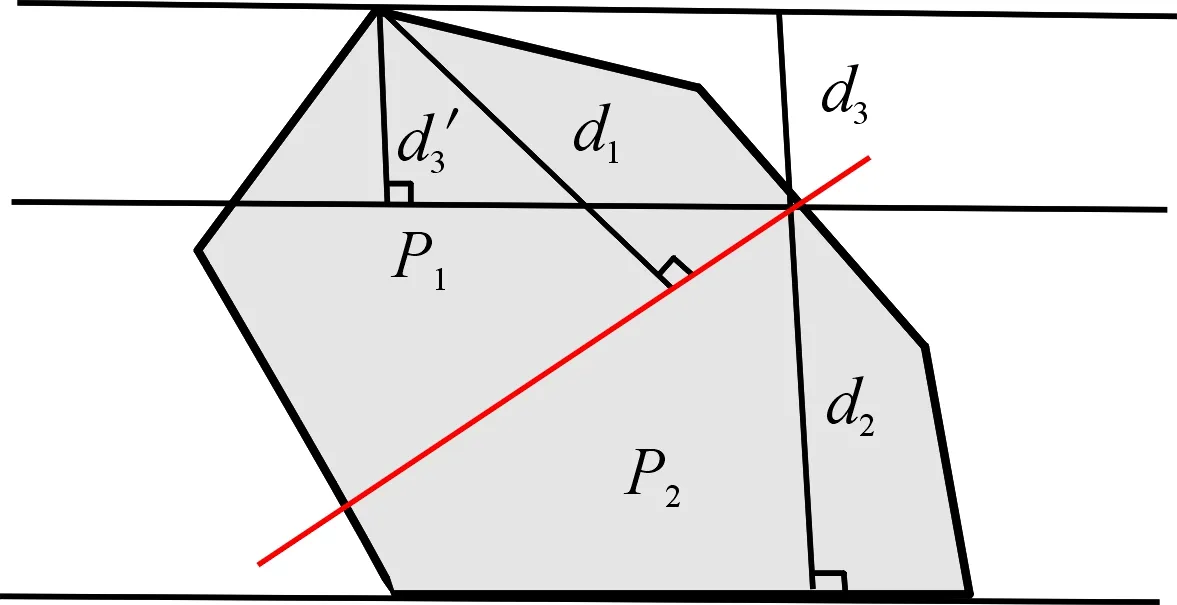
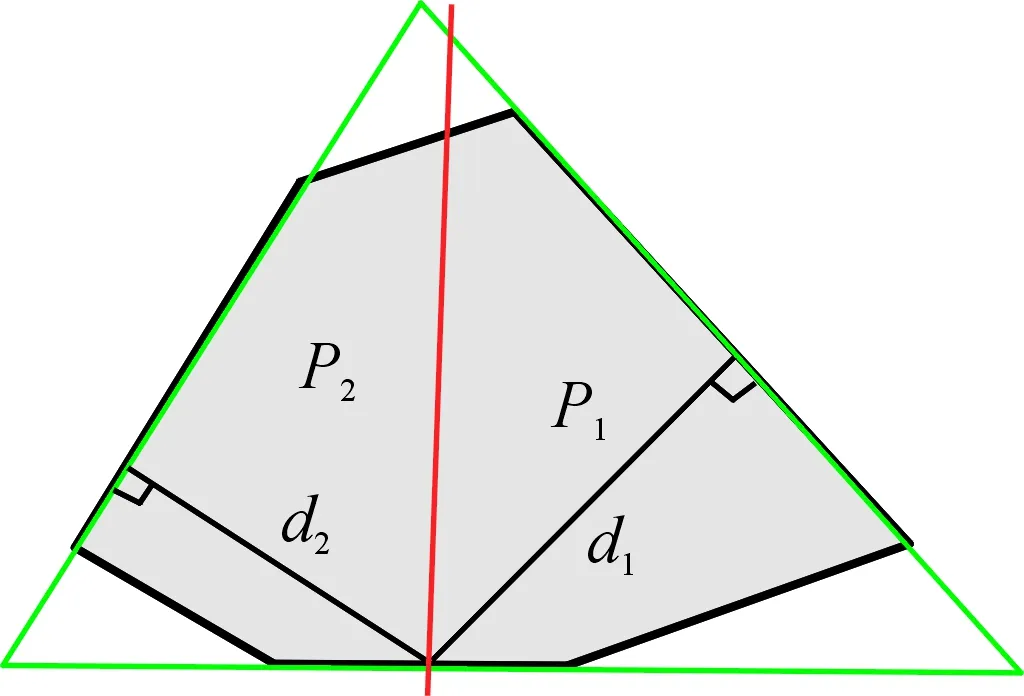
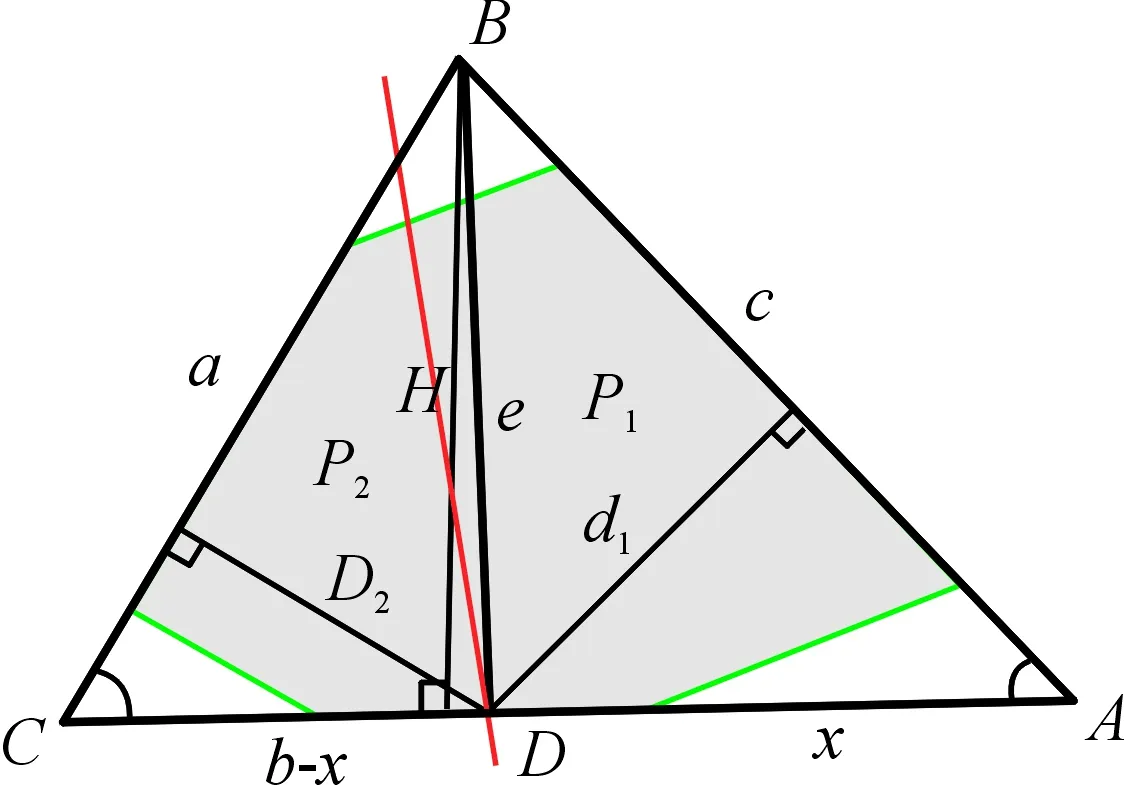
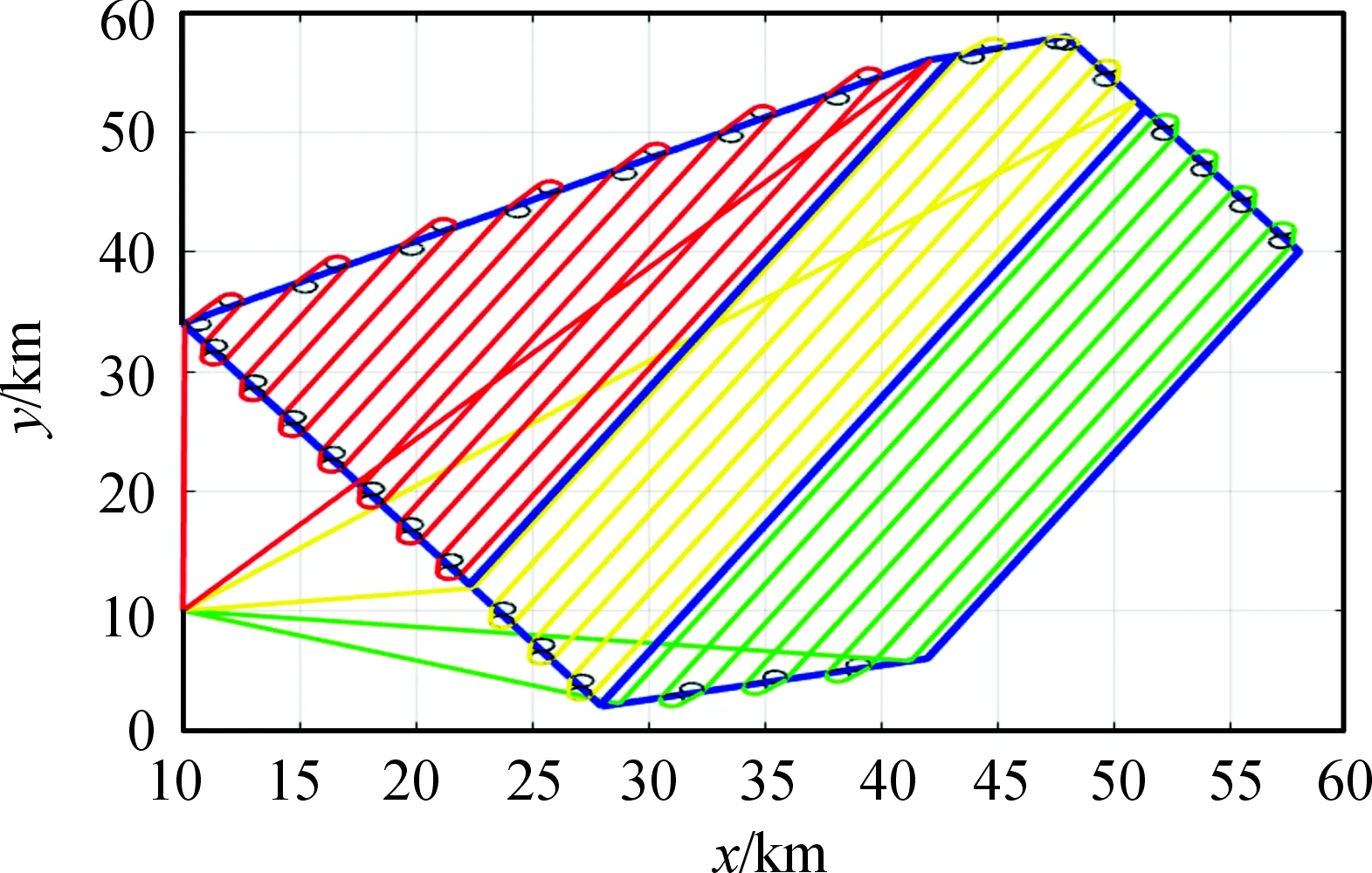
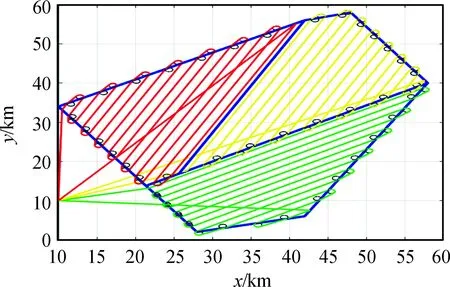
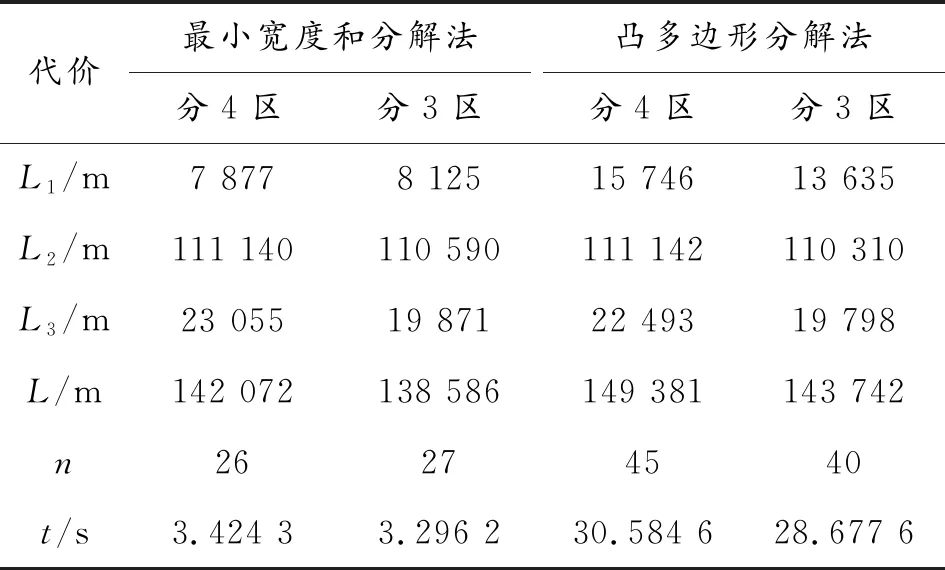
cn (1) 其中C表示无人机侦察覆盖的最大能力。 2) 无人机最小转弯半径约束,无人机在飞行速度一定的情况下在空中转弯时受离心力作用,具有最小转弯半径约束: rn≥Rmin (2) 其中Rmin为无人机的最小转弯半径。 无人机覆盖侦察的目的是对任务区域进行完全覆盖侦察,使的所有执行侦察任务的无人机飞行路径代价和最小,其目标函数为 minf=min(L)=min(L1+L2+L3) (3) 其中,L为所有无人机总的路径长度;L1为转弯过程的路径长度和;L2为任务区域扫描线的长度和;L3为无人机从地面站到任务区域以及完成任务后返回地面站的距离和。 文献[7-8]中,均提出了相应的区域分解方法,但都只是针对某种特定形状的任务区域(如三角形、矩形)进行分解,不适用于其他形状的任务区域。文献[11]从能量、飞行路程和时间的角度分析了无人机转弯过程的低效性,因此在进行无人机覆盖航迹规划时,应当尽量规划较少的转弯次数,用来降低侦察时间和路程代价,提高侦察效率。为减少所有区域内部任务机的转弯次数,本文提出了一种分解方法,可有效解决各类凸多边形任务区域的分解问题(三角形、矩形均属于凸多边形),依据凸多边形宽度和最小的方向确定区域分解方向,根据区域的大小以及各任务机执行任务的能力确定子区域数量,来实现目标区域的分解,如图2所示,一个凸多边形任务区域沿宽度方向分解为n个子区域。 图2 凸多边形区域分解示意图 文献[11]给出了凸多边形跨度和宽度的定义:在平面上两条相距足够远的平行线向凸多边的中心靠拢,两条平行线均与凸多边形相交即停止移动,此时两条平行线之间的距离即为凸多边形的跨度Ds。所有跨度中的最小值即为凸多边形的宽度d。如图3所示,凸多边形两边的平行线称为凸多边形的支撑平行线,且凸多边形的宽度只可能出现在“点边式”跨度中。 图3 凸多边形的跨度和宽度 命题:对一凸多边形,任意分解成多个子凸多边形后,各个子凸多边形的宽度和不小于原凸多边形宽度。 首先考虑将任意凸多边形分解为两个凸多边形的情况。假设原凸多边形为P,宽度为d,两个子凸多边形分别为P1、P2,对应的宽度为d1、d2。 根据确定子凸多边形宽度所对应的凸多边形顶点和边与分割线的关系,有以下几种情况: 情况1:至少有一个子凸多边形宽度所对应的顶点和边都不在分割线上; 情况2:两个子凸多边形宽度所对应的顶点或边在分割线上,又可细分为以下3种情形: Case1:两个子凸多边形宽度所对应的边都在分割线上; Case2:一个子凸多边形宽度所对应的边在分割线上,另一个子凸多边形宽度所对应的顶点是分割线与原凸多边形的交点; Case3:两个子凸多边形宽度对应的顶点都是分割线与原凸多边形的交点,但两个子凸多边形宽度对应的顶点有可能是同一顶点,也有可能不相同。 对情况1证明如下: 如图4所示,假设子凸多边形P1宽度所对应的顶点和边都不在分割线上,又P1的宽度是其本身的最小跨度,而切割线并没有使P1产生更小跨度,所以新凸多边形P1的宽度为原凸多边形P的宽度,即:d1=d,又d2>0,则d1+d2>d。 图4 情况1 对情况2证明如下: 对Case1有如下形式:作平行于分割线的原凸多边形P的两条支撑平行线,如图5,则两个子凸多边形P1、P2的宽度之和d1+d2为原凸多边形P的两个支撑平行线的距离即原凸多边形的一个跨度,根据跨度的定义可得d1+d2≥d。 图5 情况2(Case1) 对Case2有如下形式:假设子凸多边形P1的宽度所对应的边在分割线上,子凸多边形P2宽度所对应的顶点是分割线与原凸多边形的交点。 如图6:过子凸多边形P2宽度所对应的顶点作P2宽度所对应的边的平行线以及与其平行的原凸多边形P的两条支撑平行线,假设子凸多边形P2的宽度所对应的顶点到另一条支撑平行线的距离为d3,则d2+d3为两个支撑平行线的距离即原凸多边形P的一个跨度,按宽度的定义得d2+d3≥d,按平行线平移d3至d3′ 位置,可得在以d3′ 为直角边直角三角形中,斜边为d1的一部分,即d1>d3′=d3。又因为d2+d3≥d,则d1+d2≥d。 图6 情况2(Case2) 对Case3有如下形式: 当两个子凸多边形宽度所对应的顶点不是同一个点。如图7:分别作与两个子凸多边形宽度所对应的边平行的原凸多边形P的两组支撑平行线,再过两个子凸多边形各自宽度所对应的顶点作其本身宽度所对应的边的平行线,假设与子凸多边形P1宽度所对应的边平行的原凸多边形的一组支撑平行线的距离小于另一组,则同情况2(Case2):d1+d3为原凸多边形的一个跨度,d1+d3≥d,平行线内同时平移d1至d1′,d3至d3′位置。可得在以d3′为直角边的直角三角形中,斜边为d2′的一部分,则d2′=d2>d3′ =d3。又因为d1+d3≥d,则d1+d2≥d。 图7 情况2(Case3)假设1 当两个子凸多边形宽度所对应的顶点是同一个点。 如图8:分别向两边延长两个子凸多边形宽度所对应的边,再向两边延长两个子凸多边形的宽度所对应顶点所在的原凸多边形的边,三条延长线相交为一个三角形,称为原凸多边形的外切三角形,可以得出原凸多边形的宽度d必然小于或等于其外切三角形在凸多边形定义下的宽度,因为三角形最长边上的高是其最小跨度,设为H,则H≥d;将问题转化为:三角形边上的任意一点到另外两个边上的距离之和d1+d2大于三角形最长边上的高H,即d1+d2≥H。 图8 情况2(Case3)假设2 根据点是否在三角形最长边上分为两种情况:点在最长边上如图9:设AB=c,BC=a,AC=b,BD=e,AD=x;由三角形性质可知b≥c,b≥a;由凸多边形宽度的定义可知在三角形CBD中宽度的在CB上则a为三角形CBD的最长边,即:a>b-x,a>e;同理在三角形ABD中有:c>x,c>e;d1=x*sin(A),d2=(b-x)*sin(C),H=a*sin(C); (4) 当a≥c时: (5) 当a (6) 则得证。 图9 情况2(Case3)假设2(1) 点不在最长边上 如图10:设AB=c,BC=a,AC=b,BD=e,AD=x,∠ACB记为∠C; 由三角形性质可知c≥a,c>b; 由凸多边形宽度的定义可知在三角形CBD中宽度的在CB上则a为三角形CBD的最长边,即:a>b-x,a>e; 同理在三角形ABD中有:c>x,c>e;d1=x*sin(A),d2=(b-x)*sin(C),H=a*sin(C); (7) 又c≥a,则: (8) 即: (9) 得证。 图10 情况2(Case3)假设2(2) 则可得当顶点在同一个点上时d1+d2≥H≥d,得证。 综上,将凸多边形分解为两个子凸多边形后,子凸多边形的宽度之和不小于原凸多边形的宽度,即d1+d2≥d。 同理,将子凸多边形继续分解为n个子凸多边形,由数学归纳法很容易得出d≤d1+d2≤d1+d2+d3≤…≤d1+d2+…+dn。 证毕。 由此可以得出:沿着垂直凸多边形宽度方向分解得到的各个子凸多边形宽度和的最小值等于原凸多边形的宽度,则说明凸多边形区域的最优分解方式是沿着凸多边形宽度的垂直方向进行分解。 在无人机航程及载荷性能一定的条件下,其所能侦察覆盖的面积也是一定的,所以各子区域的面积也应该符合无人机所能侦察覆盖的能力范围。而无人机可侦察覆盖的能力是根据无人机自身的性能、飞行速度、高度以及载荷的参数决定。用C表示无人机侦察覆盖的能力。用p表示额外损耗率,即在规划任务时需留有一定裕度用以应付突发情况和任务机往返。用S表示任务区域的总面积。 则子区域数量为 (10) 确定了子区域的数量,则在垂直区域宽度方向将任务区域按照面积等分原则,分成n份即可。 “Z”字形模式[12]如图11所示,是一种简洁实用的覆盖方式,也是国内外研究无人机覆盖侦察最主要的方式之一,其优点是无人机在覆盖侦察过程中对任务区域可以完全覆盖侦察且重复率小。 图11 Z字形扫描模式 当无人机以不同飞行方向侦察同一任务区域时,其路径代价也不同,如图12所示。文献[11]证明了沿着垂直于宽度方向侦察,无人机的转弯次数较小,飞行路程短,侦察效率高。 图12 飞行方向对航迹的影响示意图 文献[13]针对任务机的最小转弯半径Rmin以及和任务载荷有关的航带间距和旁向重叠率的关系,提出了η形转弯方法,并证明了η形转弯方法相对其他转弯方法的优越性。转弯方式如图13所示。 图13 η形转弯方法示意图 一种改进的多无人机覆盖航迹规划方法步骤如图14所示: 图14 航迹规划方法步骤框图 步骤1确定分解方向。根据任务区域的坐标,计算凸多边形所有的跨度,其中跨度最小的方向作为凸多边形宽度的方向,凸多边形的分解方向便是宽度的垂直方向。 步骤2求解子区域数量。根据任务区域的面积和无人机执行任务的能力及其额外损耗率,求解无人机数量即区域分解数量。 步骤3按照由步骤1、步骤2求解的区域分解方向和分解数量进行任务区域分解。 步骤4规划各任务航迹。根据起始位置坐标和无人机最小转弯半径,无人机高度以及载荷参数,按照“Z”字形覆盖方式进行各区域内部航迹规划。 实验平台为Inter Core i5-7300HQ CPU,8GB,64位Win10操作系统惠普笔记本。编程工具为Matlab R2017b(64位)。 仿真实验的参数来源于XR-4型无人机,主要参数如表1所示。 表1 仿真参数设置 凸多边形任务区域顶点坐标分别是(2 800,200),(4 200,600),(5 800,4 000),(4 800,5 800),(4 200,5 600),(1 000,3 400)。地面站坐标为(1 000,1 000),以上坐标的单位均是m。 图15和图17分别为分4个子区域和3个子区域时用本文提出的最小宽度和分解法所得的多无人机覆盖扫描航迹,图16和图18分别为分4个子区域和3个子区域时用文献[8]所提出的凸多边形分解法所得的多无人机覆盖扫描航迹。其路径代价如表2所示。 图15 分4个子区域时最小宽度和分解方法 图16 分4个子区域时凸多边形分解法 图17 分3个子区域时最小宽度和分解方法 图18 分3个子区域时凸多边形分解法 表2 两种区域分解方法的航迹路径代价 结果分析如下: 1) 数据L1为两种分解法转弯过程的飞行路径代价,可以看出由于分解方式的不同转弯过程的路径代价差距非常大,所提最小宽度和分解法的转弯过程路径代价和原有的凸多边形分解法转弯过程路径代价差距非常大,可以说明最小宽度和分解法的优越性。 2) 数据L2可以看出扫描线路径代价基本相同,进一步验证了对于覆盖扫描方式来说,对扫描效率影响的主要因素不是直线扫描部分,而是转弯部分。 3) 数据L为两种分解法的总路径代价,可以看出最小宽度和分解法比凸多边形分解法路径代价减少了5.14%和3.72%,表明最小宽度和分解法可以有效降低路径代价,对任务完成有利。 4) 数据n为转弯次数,可以看出最小宽度和分解法转弯次数明显少于原有的凸多边形分解法,有效提高了无人机的侦察效率。 5) 从仿真损耗时间t可以看出,最小宽度和分解法的仿真损耗时间远远少于与原有的凸多边形分解法的损耗时间,提高了航迹规划效率。 1) 通过证明凸多边形任意分解成多个子凸多边形后,各个子凸多边形的宽度和不小于原凸多边形宽度,得出沿宽度方向分解时,子区域宽度和最小。 2) 使用所提分解方法根据无人机的能力和任务区域的大小来确定分区的个数,使无人机在任务区域内扫描的总转弯次数最少,相对于现有的分解方法路径代价小,算法效率高。 3) 在各个区域内部使用“Z”字形扫描方式,根据最小转弯半径结合η形转弯方法,使子区域内部侦察扫描效率更高。 4) 在今后的研究中可进一步讨论异构无人机根据能力大小分区的区域配置以及多无人机覆盖侦察多区域的任务分配以及路径规划。2 区域分解方法
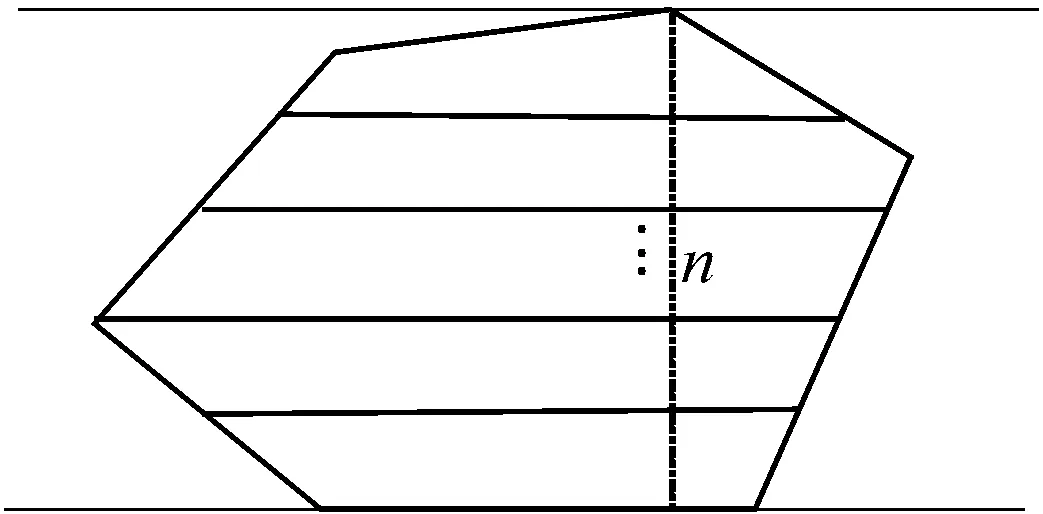
2.1 区域分解方向
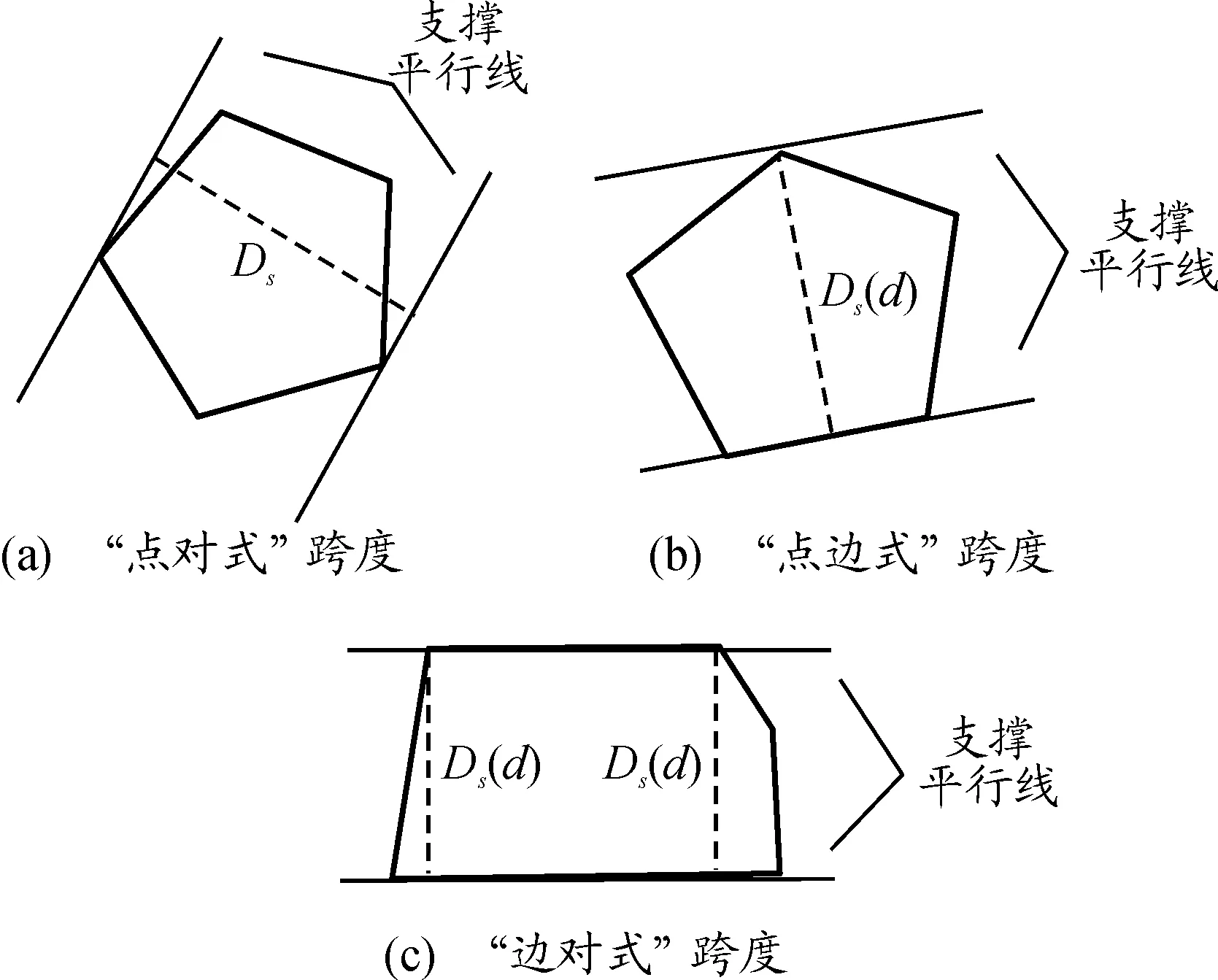
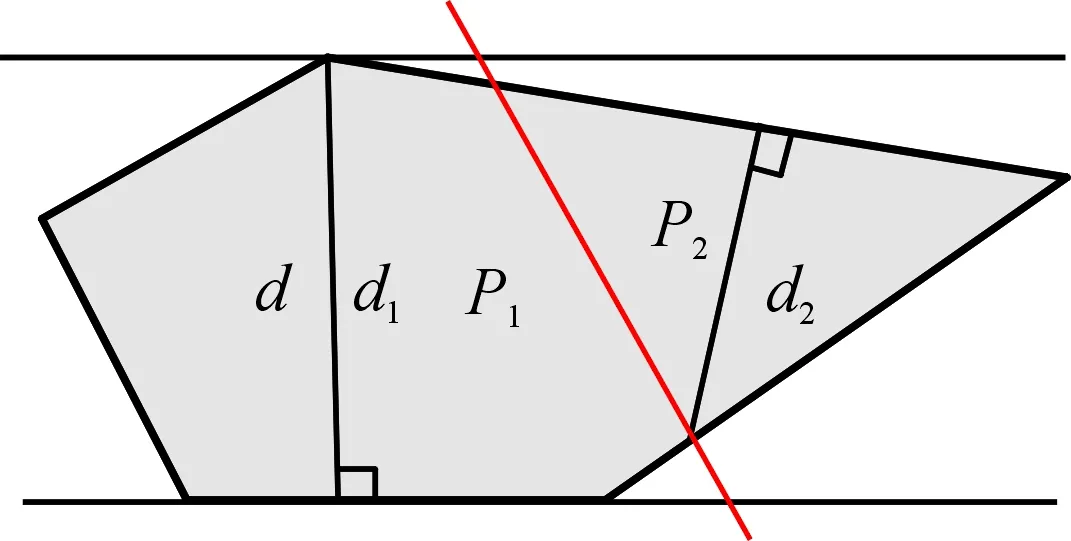

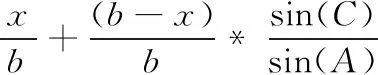
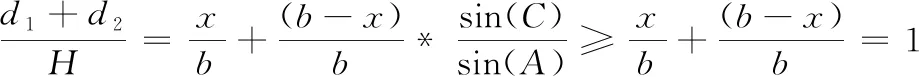

2.2 区域分解数量
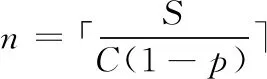
3 航迹规划方法
3.1 侦察扫描方式
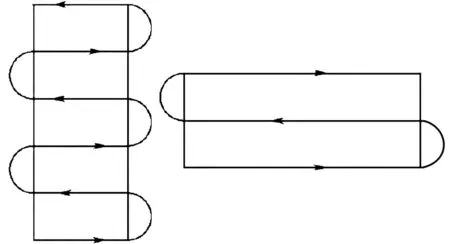
3.2 η形转弯方法
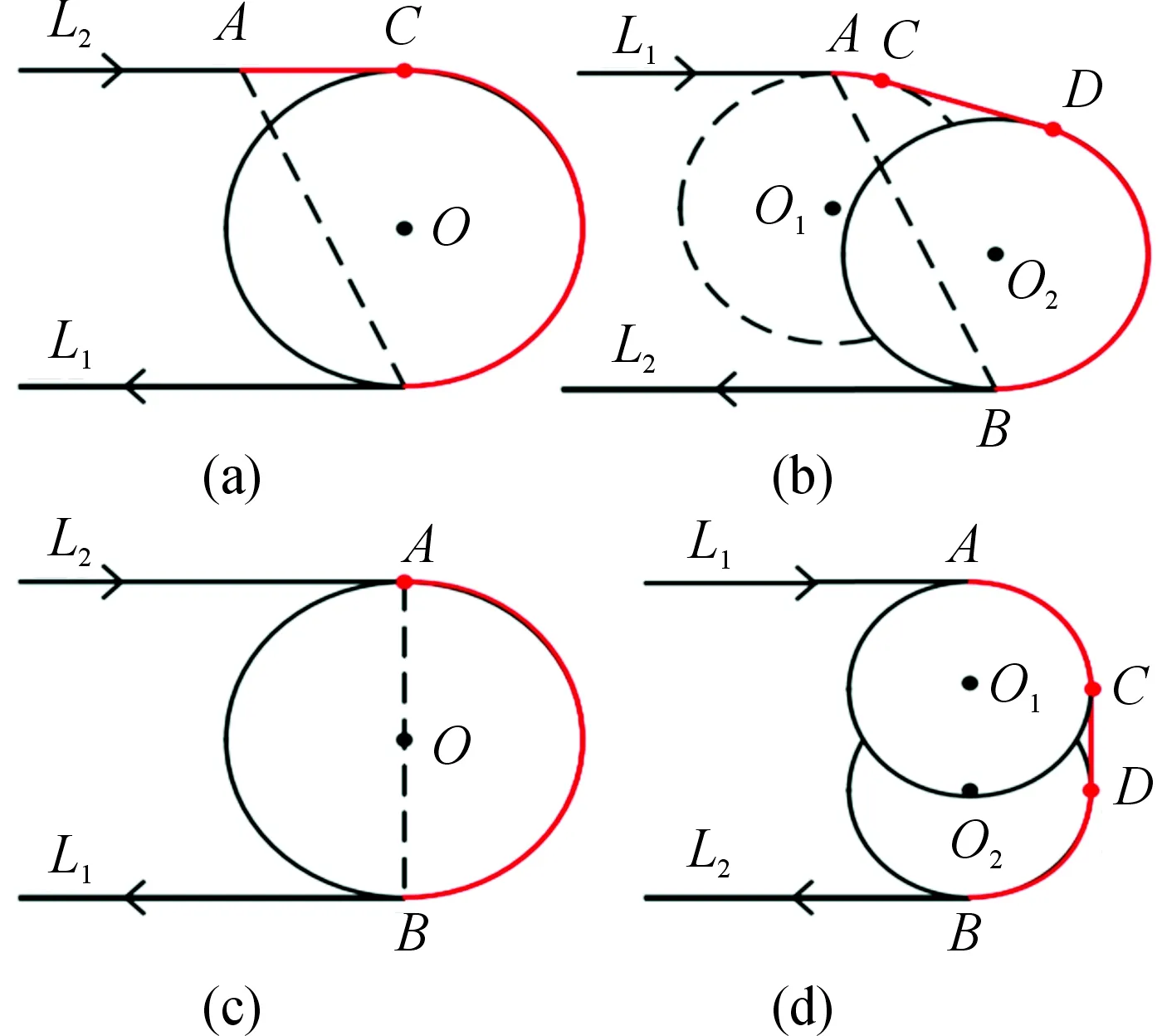
4 方法步骤
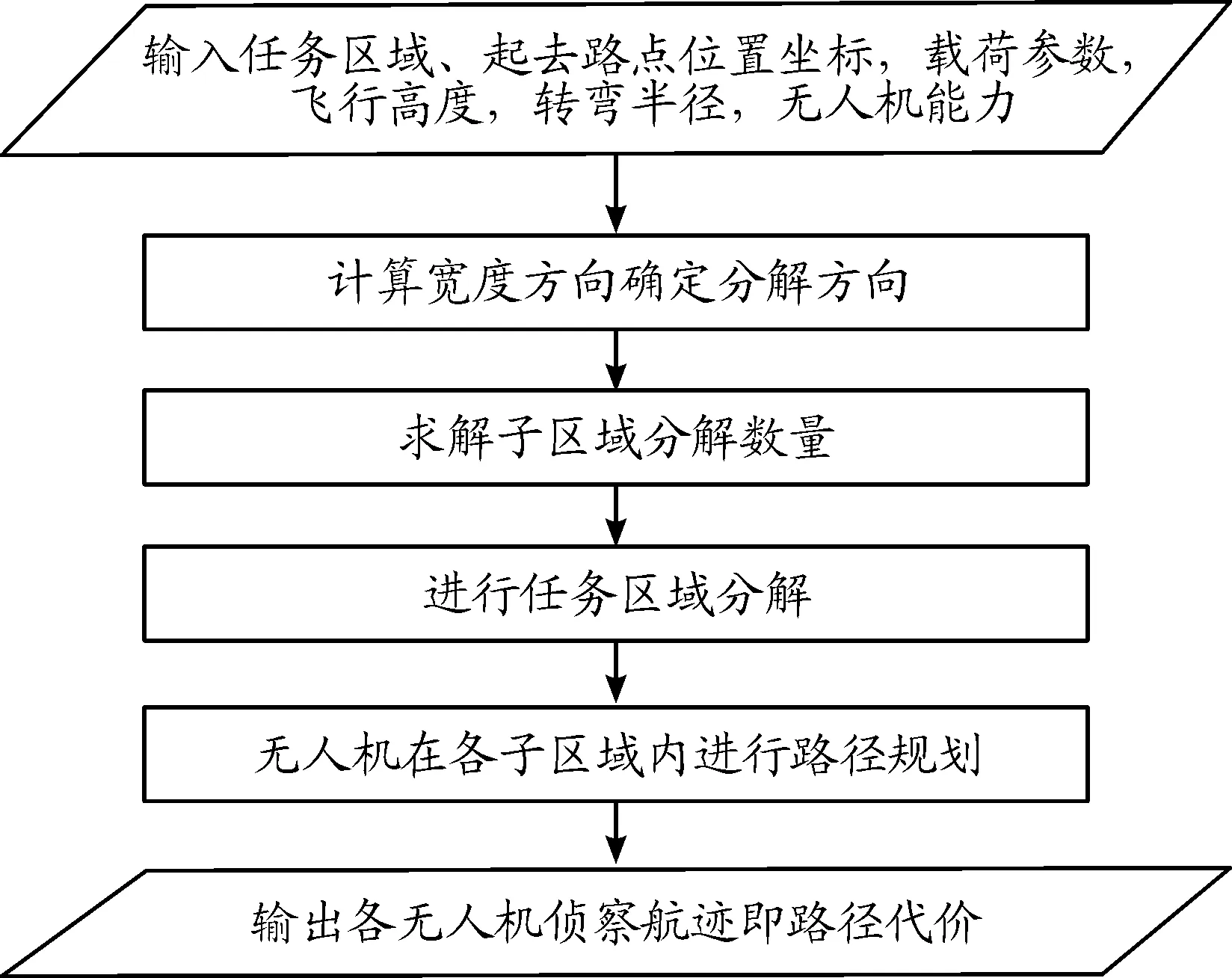
5 仿真实验
5.1 实验设置

5.2 仿真结果及分析
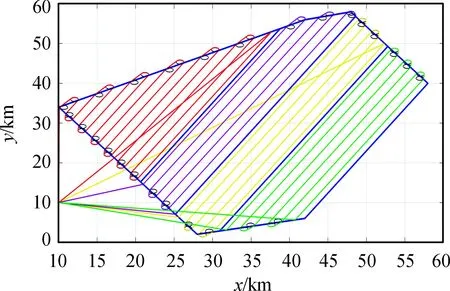

6 结论
