无人机发射过程风载荷影响分析
2020-11-05陈刚
陈 刚
(南京模拟技术研究所, 南京 210016)
小型无人机由于体积小、造价低、飞行包线大、战场生存力强及无人员伤亡等特点,已广泛应用在航空侦察、干扰、模拟靶标、校射等军事领域以及航拍、地质测量等民用领域。无人机的相关技术研究已经成为国内外的研究热点[1-2]。
无人机的发射方式有很多,其中使用火箭助推发射,具有便捷、快速,对发射场地无严格要求,适合于野战环境等优点,随着无人机的发展,火箭助推发射方式得到了广泛研究与应用[3-4]。
对火箭助推无人机发射阶段的动力学响应和安全性分析,已有一些学者开展了相关研究。田新锋等[5]建立了发射阶段的数学模型,确定了某无人机安全发射区域。杨广等[6]运用Matlab编写了发射段的飞行仿真程序,开展了发射段的仿真分析。许军等[7]对比分析了有风(恒定风速)与无风状态下火箭助推发射方式下的动态响应。刘付平等[8]建立了发射阶段动力学模型,仿真计算了助推火箭安装偏差对无人机发射安全的影响。
综上所述,采用火箭助推发射方式的无人机,发射安全性受到的影响因素较多,但在吊挂偏差和发射架扰动控制较好的前提下,风载荷成为影响发射安全性的主要因素。
本文以某型号火箭助飞无人机为研究对象,采用联合仿真方法,在ADAMS中建立了可考虑吊挂偏差和发射架扰动影响的发射段动力学模型,在MATLAB中建立了飞控系统模型,实现了该型无人机的受控发射仿真分析;采用“风剖面”与“瞬态中国帽”法建立了动态风场模型,仿真计算了风速、风向、平均风、瞬态风等因素对无人机发射安全性的影响。研究结果可为该型无人机的研制提供参考。
1 发射动力学联合仿真模型建立
无人机火箭助推发射系统主要包括发射架、无人机和助推火箭3个部分。无人机机身前方有2个支撑轴约束在翻转架上,后下方有一个支撑,约束在支撑导轨内,无人机下方后端装有助推火箭。发射架主要由架体、翻转架、后支撑、闭锁销等组成,结构示意图如图1。
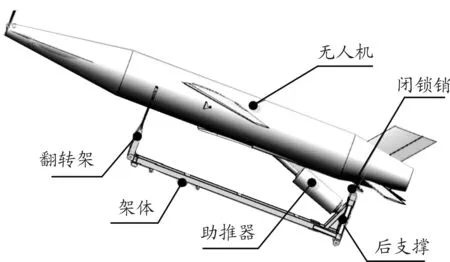
图1 无人机火箭助推系统结构示意图
助推火箭达到一定的推力时,闭锁销被剪断,无人机在翻转机构与后支撑的约束下离开发射架,当助推火箭工作结束后,与无人机自动分离。
本文主要研究风载荷对发射安全性的影响,故在建立无人机发射动力学模型的过程中,为了突出主要问题,对模型进行了如下假设:
1) 将无人机和发射架简化为刚体;
2) 在发射过程中,不考虑燃油晃动导致的质心位置偏移;
3) 认为吊挂精度较高,助推器推力线通过飞机重心;
4) 环境温度为常温(20 ℃)。
将无人机火箭助推发射系统的三维数模导入ADAMS中,根据设计参数,对各部件赋予质量属性。根据约束关系,添加一系列约束,包括固定副、转动副等。将2个支撑轴与翻转架之间、助推器锥座与助推器锥窝之间、后支点与后支撑导轨之间的约束关系定义为非线性接触约束。
飞机机体坐标系定义为:以无人机重心为原点,X轴沿机身向前指向机头原点,以水平向右方向为Y轴,根据笛卡尔右手坐标系建立Z轴。本文有关无人机发射过程的姿态变化,均是基于机体坐标系来研究。
助推器推力以AKISPL函数形式施加到动力学模型中。为了尽量减小接触约束导致的初始噪声,本文将助推器推力延迟0.5 s后施加。
在无人机发射阶段,需要对无人机的姿态进行控制,以确保安全发射。在无人机发射过程中,可能会因各种因素而出现较大的姿态偏差,故在助推发射过程中通常采用俯仰角和侧倾角控制。本文设定发射过程俯仰角控制目标值为15°,侧倾角控制目标值为0°。
在无人机发射阶段,需要对无人机的姿态进行控制,在ADAMS中将无人机的3个姿态角(俯仰、侧倾、偏航)、速度、加速度、高度、3个等效气动力、3个等效气动力矩,定义为状态变量,从而实现与MATLAB控制策略模型的数据实时交互。联合仿真模型原理图如图2。
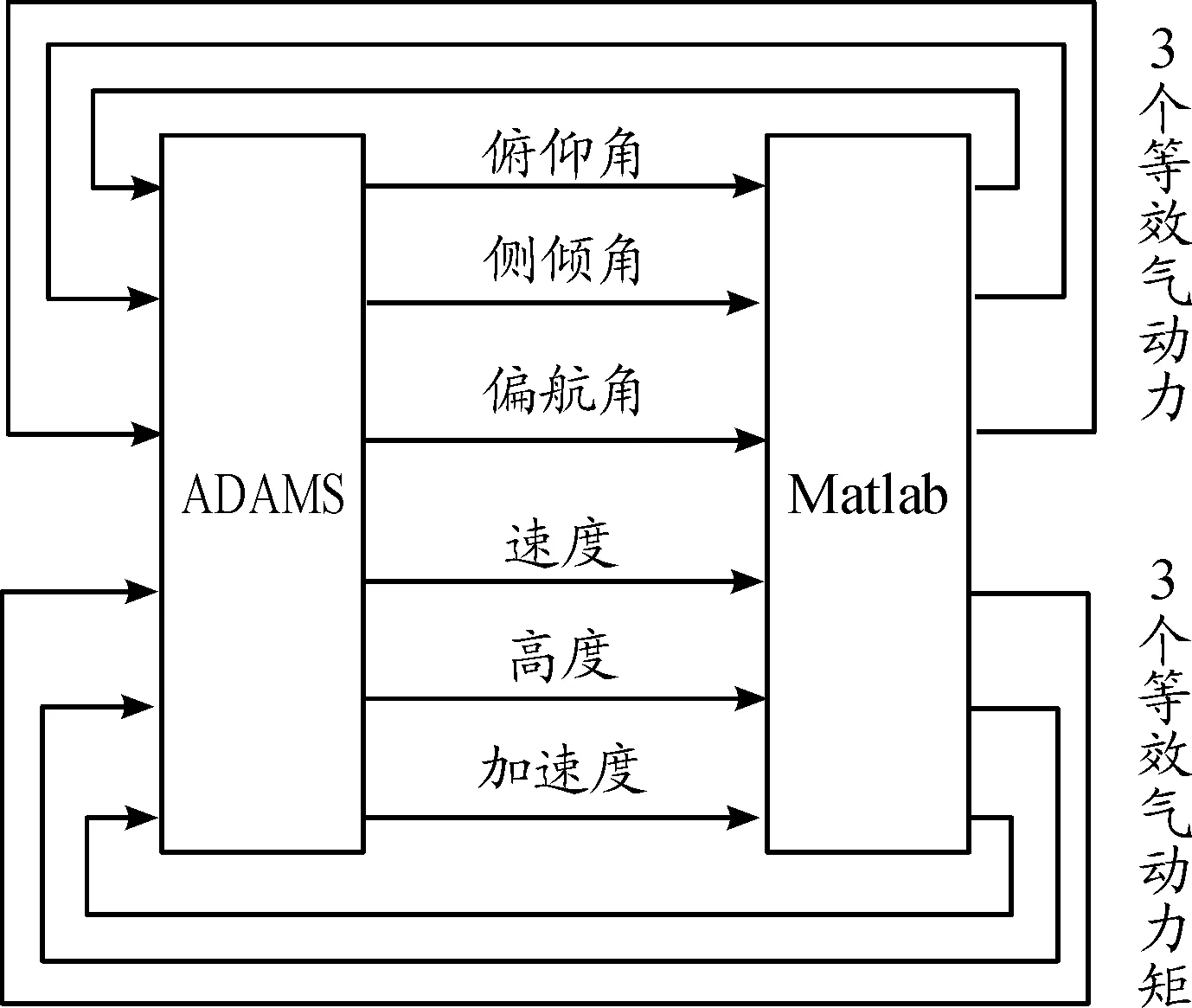
图2 联合仿真模型原理框图
2 风场模型建立
2.1 平均风剖面
风速是描述风特性的一个重要参数。由于地面的摩擦阻力的存在,越接近地面气流速度越慢,即风速越小,距离地面300~500 m处,才可以忽略地面的影响。因此为描述平均风速沿高度方向的变化规律,需引入平均风梯度,也就是风剖面的概念。平均风速沿高度变化的规律称为平均风速梯度或风剖面。平均风沿高度变化的规律有两种表达形式,即按实测结果推得的指数风剖面和按边界层理论得到的对数风剖面[9-10]。
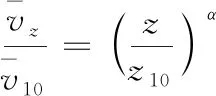
(1)
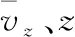

表1 粗糙度类别及粗糙度系数
根据本文研究无人机的实际使用区域规划,发射区域多处于A、B两类地形,可确定地面粗糙度系数α为0.12或者0.16。
2.2 风组成
根据大量风的实测资料,可把风分为平均风和动态风来加以分析,即:
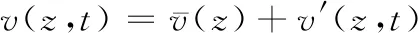
(2)
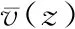
平均风是在给定的时间间隔内,把风对物体的作用力看成不随时间而改变的量,工程上将其作为静力处理。
动态风是由于风的不规则性引起的,它的强度按随机规律变化,由于周期短,其作用性质完全是动力的。动态风载荷计算通常有两种方法:根据功率密度谱函数来描述的脉动风计算方法和瞬态“中国帽”风载荷计算方法。
1) 脉动风计算方法
制定出版社企业品牌和图书品牌的出口战略,将企业出口图书的经营定位与企业品牌结合起来,打造业务优势、商业模式优势,传播企业知名度和美誉度;并在企业品牌基础上,依据图书系列和消费者偏好,打造产品品牌,形成具有中国传统文化和现代科学支撑的为恶化传播体系,张扬中国价值观、世界观。
此方法按风或脉动风作为输入,按随机振动理论直接进行计算而求得结构响应。目前应用较多的脉动风速谱有Von Karman谱、Davenport谱、Kaimal谱等。Von Karman谱采用沿高度方向变化的风速谱,其计算公式如下:
(3)
(4)
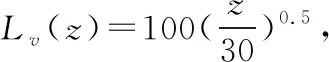
(5)
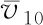
图3给出了标准高度处(10 m高度)、风速为10 m/s工况下的平均风与脉动风的时程曲线图。从图中可以看出:最大瞬时风速值约为平均风速度的1.5~1.6倍。
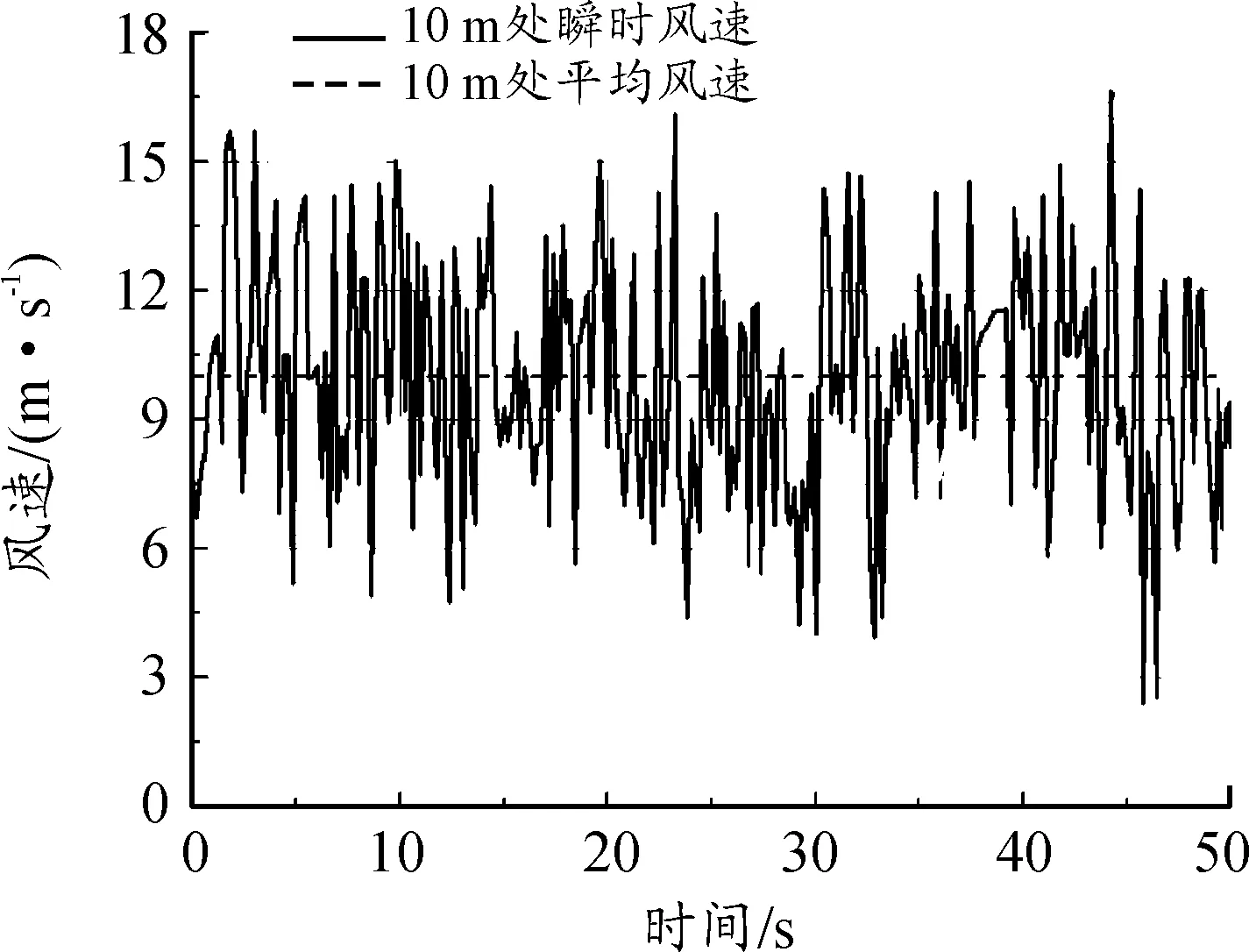
图3 10 m处平均风速与瞬时风速
2) 瞬态“中国帽”风载荷计算方法
欧洲标准EN 14067-6中的瞬态中国帽风载模型(Chinese hat)考虑了风的瞬态效应,在平均风速基础下加入瞬态风速分布模型—“中国帽”。
根据实测瞬时脉动风从0短时增大到最大风速然后又下降到0的特性,通常利用半正弦函数对实测瞬时脉动风进行模拟。此方法可以较好地模拟实测瞬时脉动风载模型,在高速列车的侧方安全性分析中得到广泛应用。
模拟瞬时脉动风速的半正弦函数表达式为:
(6)
式中:vmax为瞬时最大风速(不包含平均风速);Δt为瞬时脉动风作用时间;t0、t1为风载开始时刻、风载结束时刻。
2.3 风载荷模型确定
以上两种动态风载荷计算模型均得到广泛应用。但对于本报告研究的无人机发射过程而言,脉动风计算方法得到的风载荷,相当于在平均风附近振荡,其小于平均值的这一段,对无人机的干扰比平均风还要低,故基于该方法得到的安全裕量可能较低。
瞬态中国帽风载荷计算方法即保持了最低风速速不小于平均风速、又可以分析风的突变对发射过程的影响,故本报告采用瞬态中国帽风载荷计算方法建立无人机发射过程的风载荷模型。
文献中给出的瞬态风周期在一般在1~5 s。对于本文研究的无人机而言,由于火箭助推段无人机速度较低,气动控制效率较低,故该阶段是受风载荷影响最为严重的阶段。故本报告中取模拟瞬时脉动风的正弦函数周期为4s,即半周期为2 s,与火箭助推段时间完全一致。
为确保分析结果的安全裕量较大,本报告中的最大瞬时风速值取为对应工况下平均风速度的2.0倍。某一工况下的风速时程曲线如图4所示(取无人机质心的初始离地高度为1 m)。该工况下,标准高度10 m处的平均风速为10 m/s。

图4 某一工况下的风速时程曲线
风速是按照地面坐标系定义的,需要按照地面系到机体系的转换矩阵,将地面系下的风速分量转换到机体坐标系下。
在MATLAB中编制风剖面计算模型,将其嵌入到已建立的联合仿真模型中,实现无人机发射过程姿态变化与风场变化的耦合计算。
3 不同风载荷下的发射安全性分析
将开展逆风、顺风以及侧风作用下的发射安全性分析。风力等级分别为三级(平均风速5 m/s)和五级(平均风速10 m/s)。
3.1 平均风载荷作用下的发射过程动态响应
首先,对比给出了无风、迎风(5 m/s平均风)、迎风(10 m/s 平均风)和顺风(10 m/s平均风)工况下,无人机的离架姿态变化曲线,如图5~图8所示。
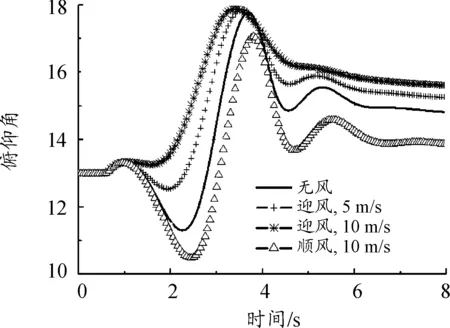
图5 俯仰角变化曲线
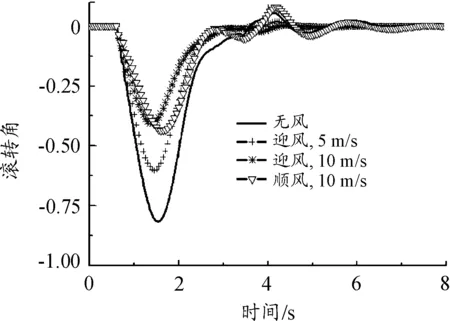
图6 滚转角变化曲线
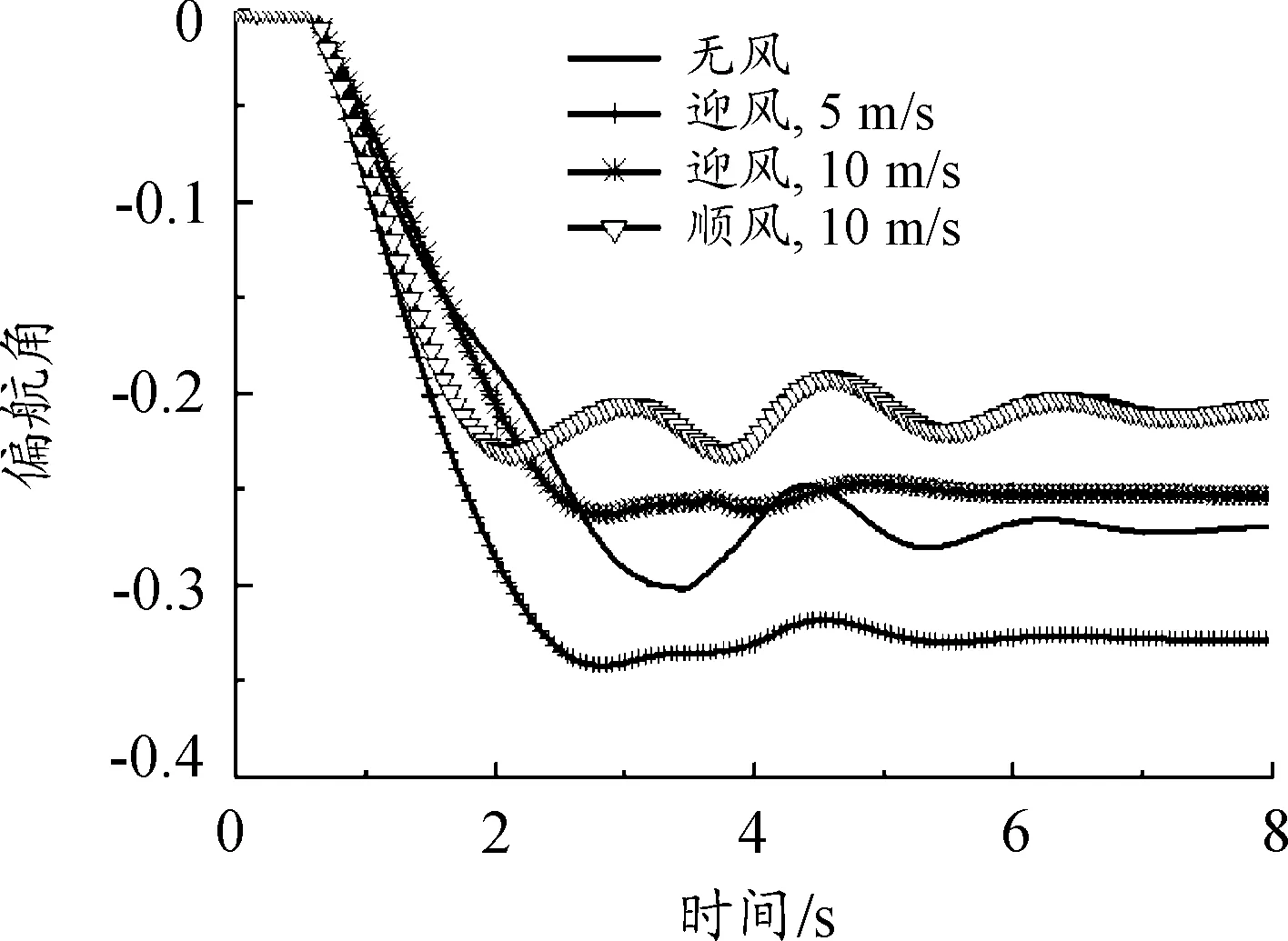
图7 偏航角变化曲线
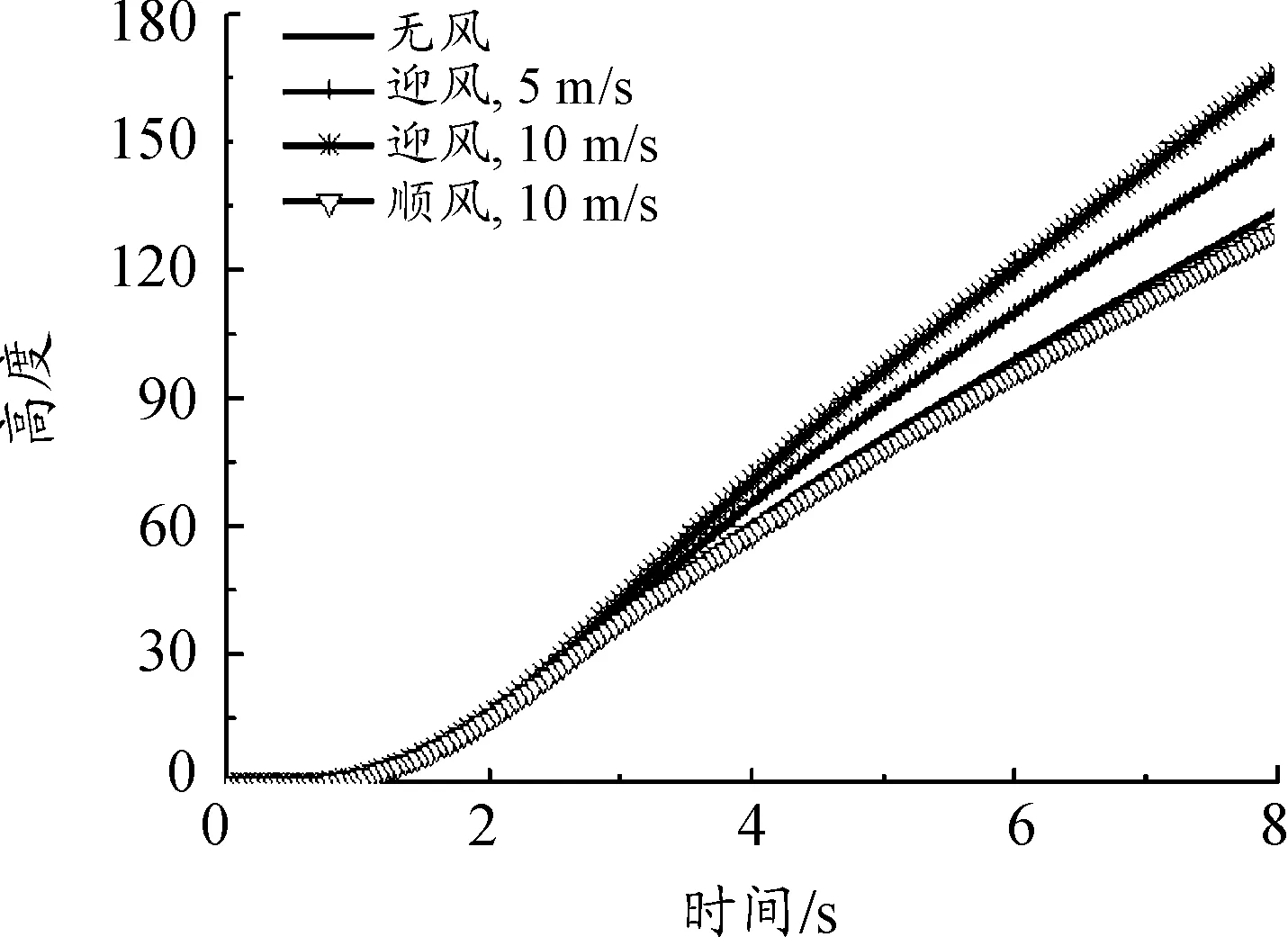
图8 高度变化曲线
从结果中可以看出:迎风发射,有利于增大飞机离架后的俯仰角,对发射安全性有利;滚转和偏航姿态的变化基本为零;同样时间内,迎风发射时的飞机高度要高于顺风发射;迎风发射时,无人机发射安全性要高于顺风发射。总体上,无风、迎风(5 m/s平均风)、迎风(10 m/s平均风)和顺风(5 m/s 平均风)工况下,无人机能够安全发射;顺风(10 m/s平均风)工况下,无人机俯仰姿态变化较大,发射安全性降低。
其次,对比给出了无风、侧风(5 m/s平均风)、侧风(10 m/s平均风)工况下,无人机的离架姿态变化曲线,如图9~图12所示。
从结果中可以看出:侧风对飞机离架后的俯仰姿态影响不大;侧风对无人机的高度影响较小;侧风风速越大,滚转和偏航姿态的变化越大;侧风载荷作用下,侧滑角的变化较为剧烈;在侧风(10 m/s平均风)工况下,无人机发射后滚转和偏航姿态变化剧烈,安全性降低。
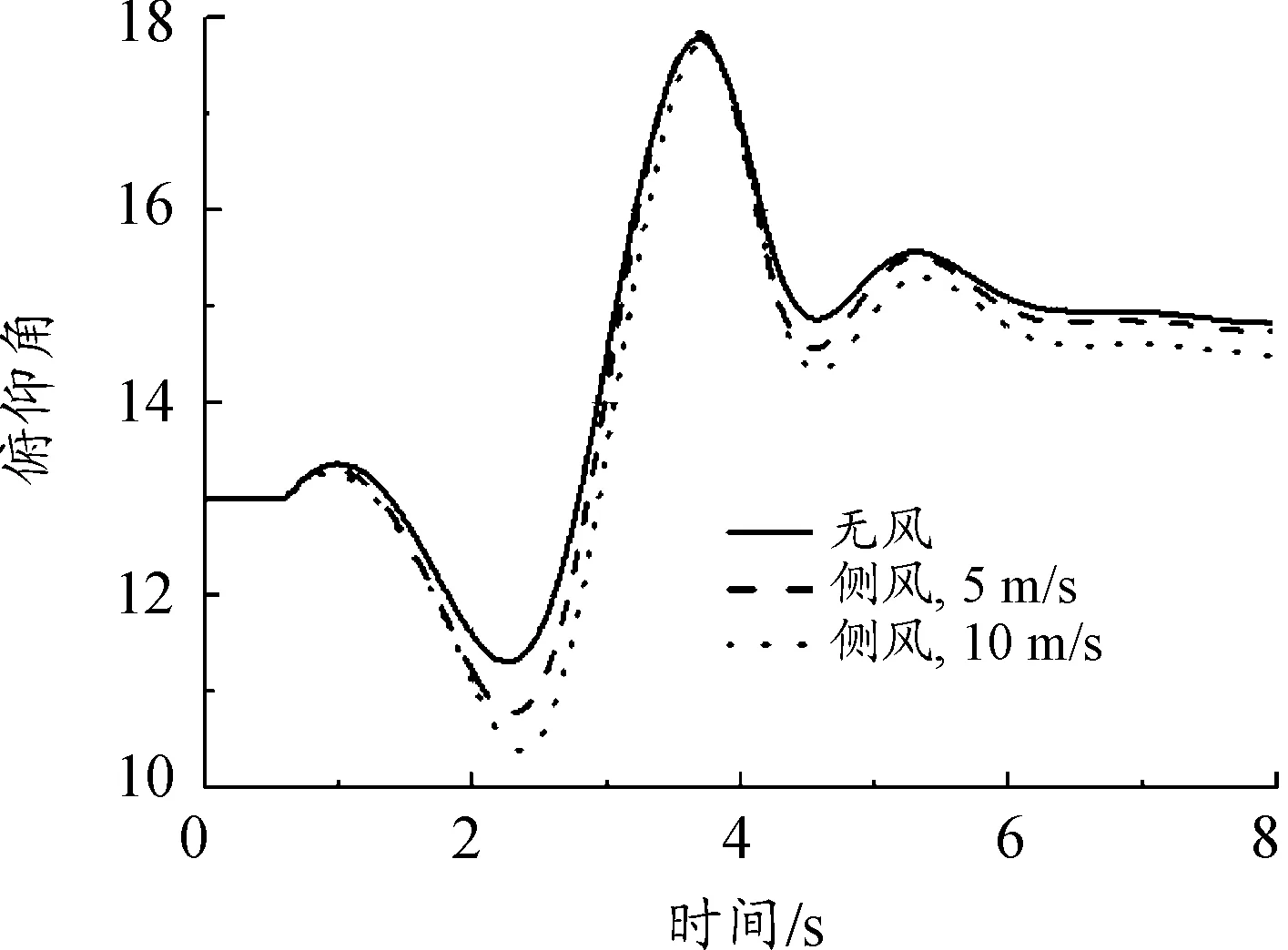
图9 俯仰角变化曲线
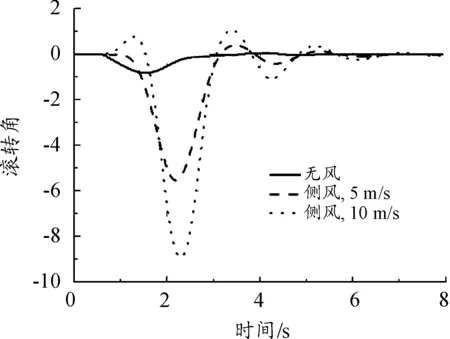
图10 滚转角变化曲线
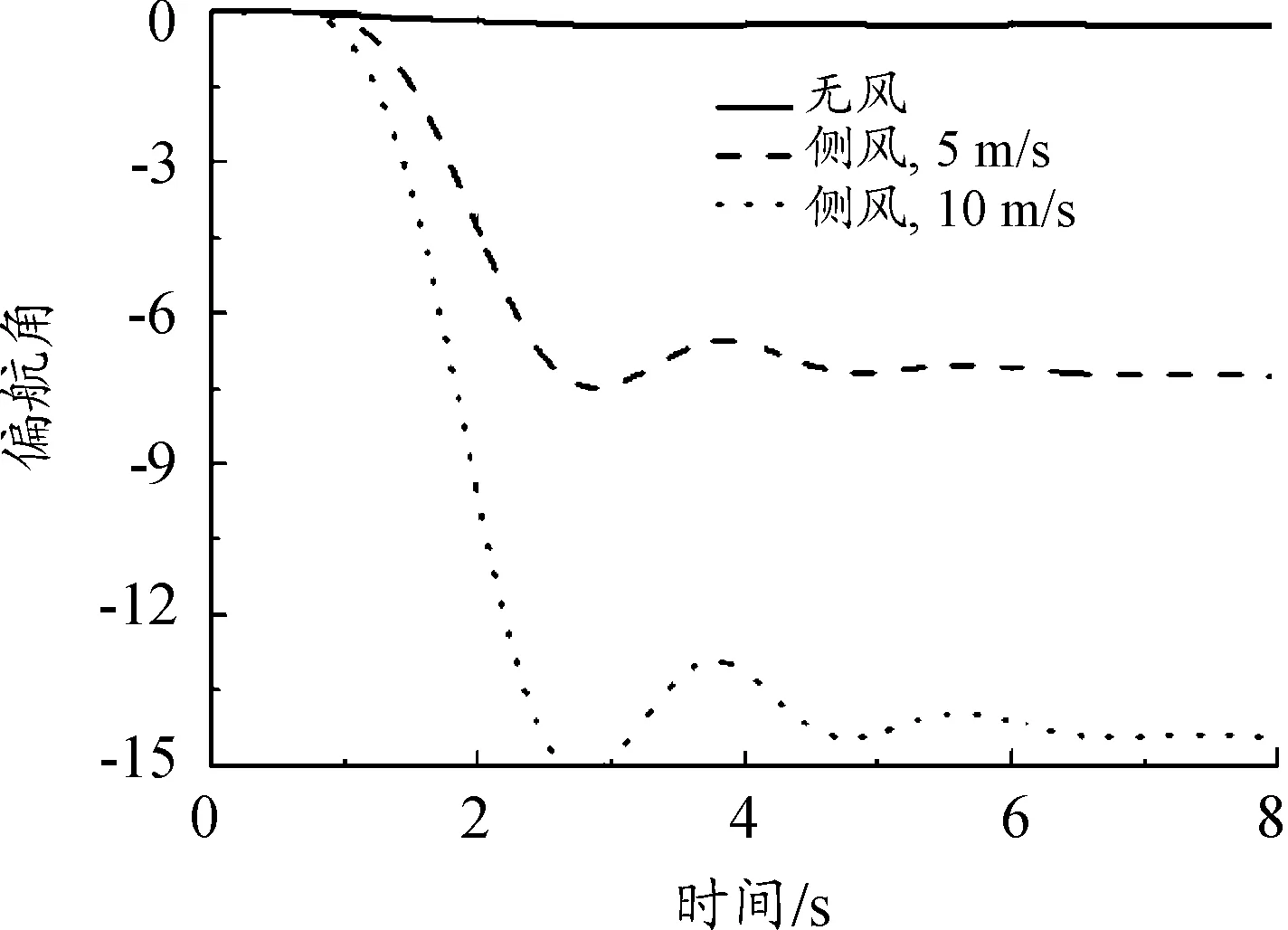
图11 偏航角变化曲线
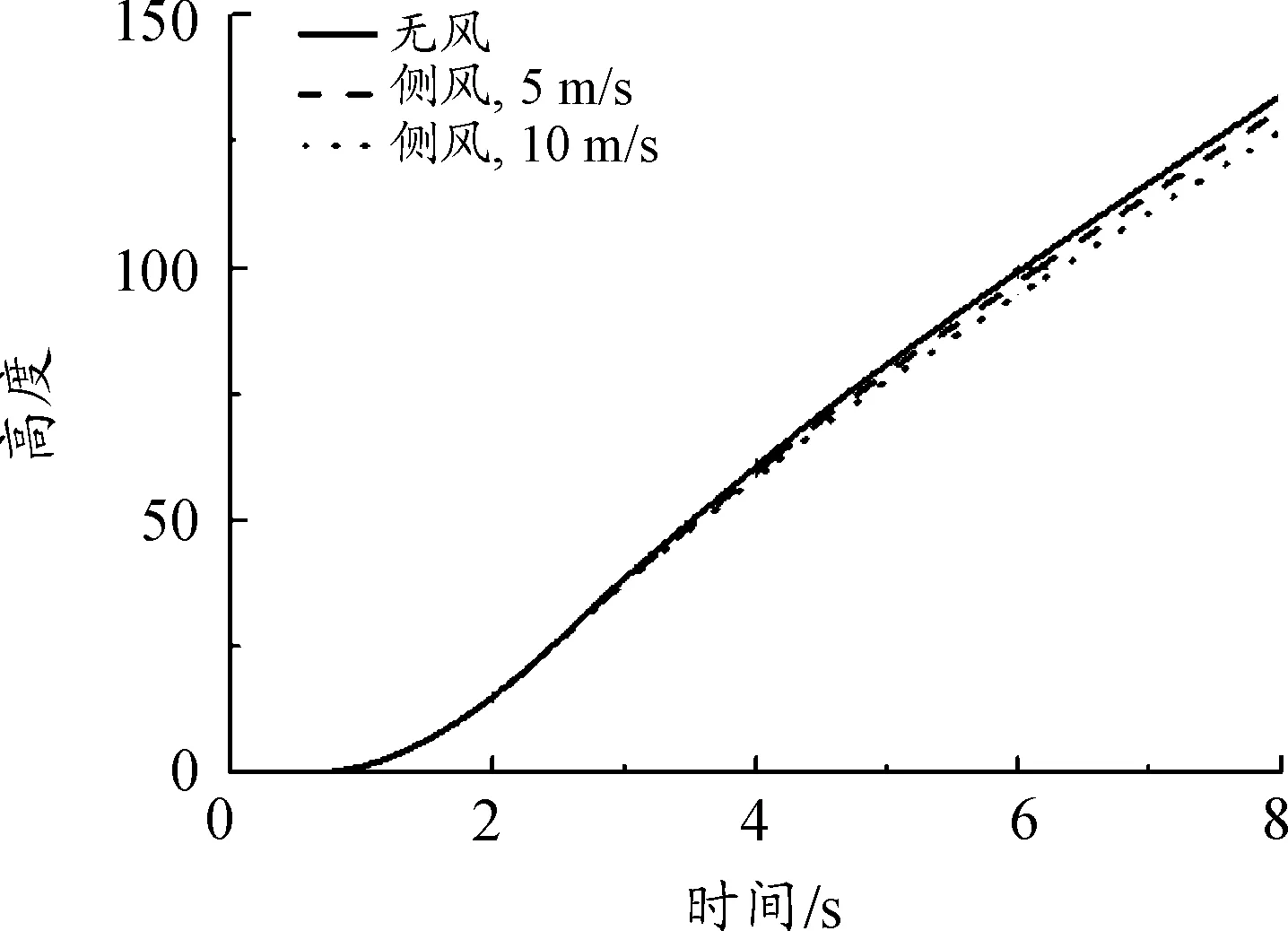
图12 高度变化曲线
3.2 瞬时脉动风载荷作用下的发射过程动态响应
对比给出了迎风(10 m/s脉动风)和顺风(10 m/s脉动风)工况下,无人机的离架姿态变化曲线,如图13、图14所示。经过前面分析可知:迎风、顺风对无人机离架姿态的影响,主要是俯仰姿态相关量,故此处不再给出其他姿态的结果。

图13 俯仰角变化曲线
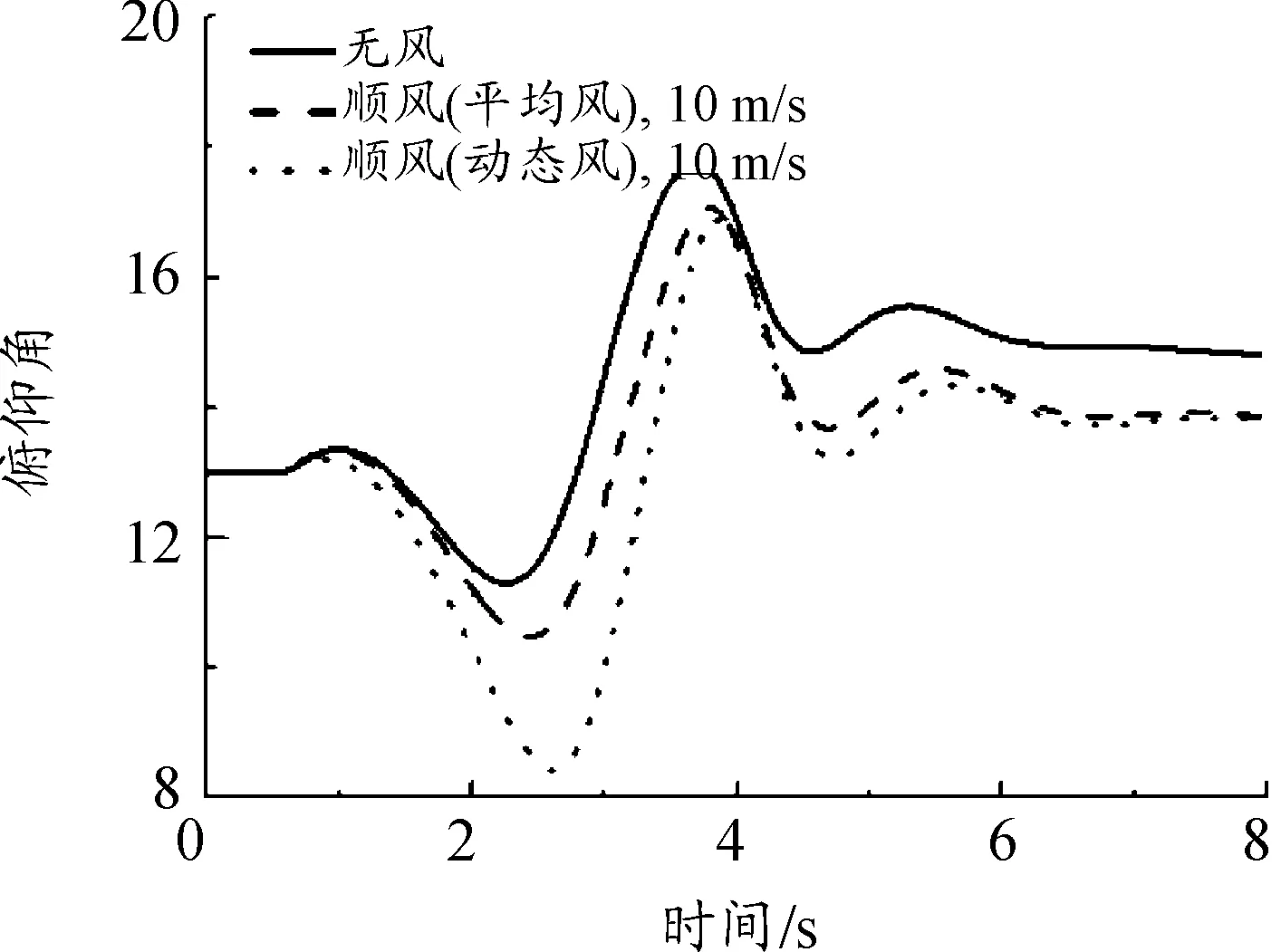
图14 俯仰角变化曲线
从结果中可以看出:相比于平均风工况结果,脉动风作用下的无人机俯仰姿态变化幅度增大,无人机出架后低头姿态明显,发射安全性降低。
其次,对比给出了无风、侧风(5 m/s脉动风)、侧风(10 m/s 脉动风)工况下,无人机的离架姿态变化曲线,如图15~图18所示。
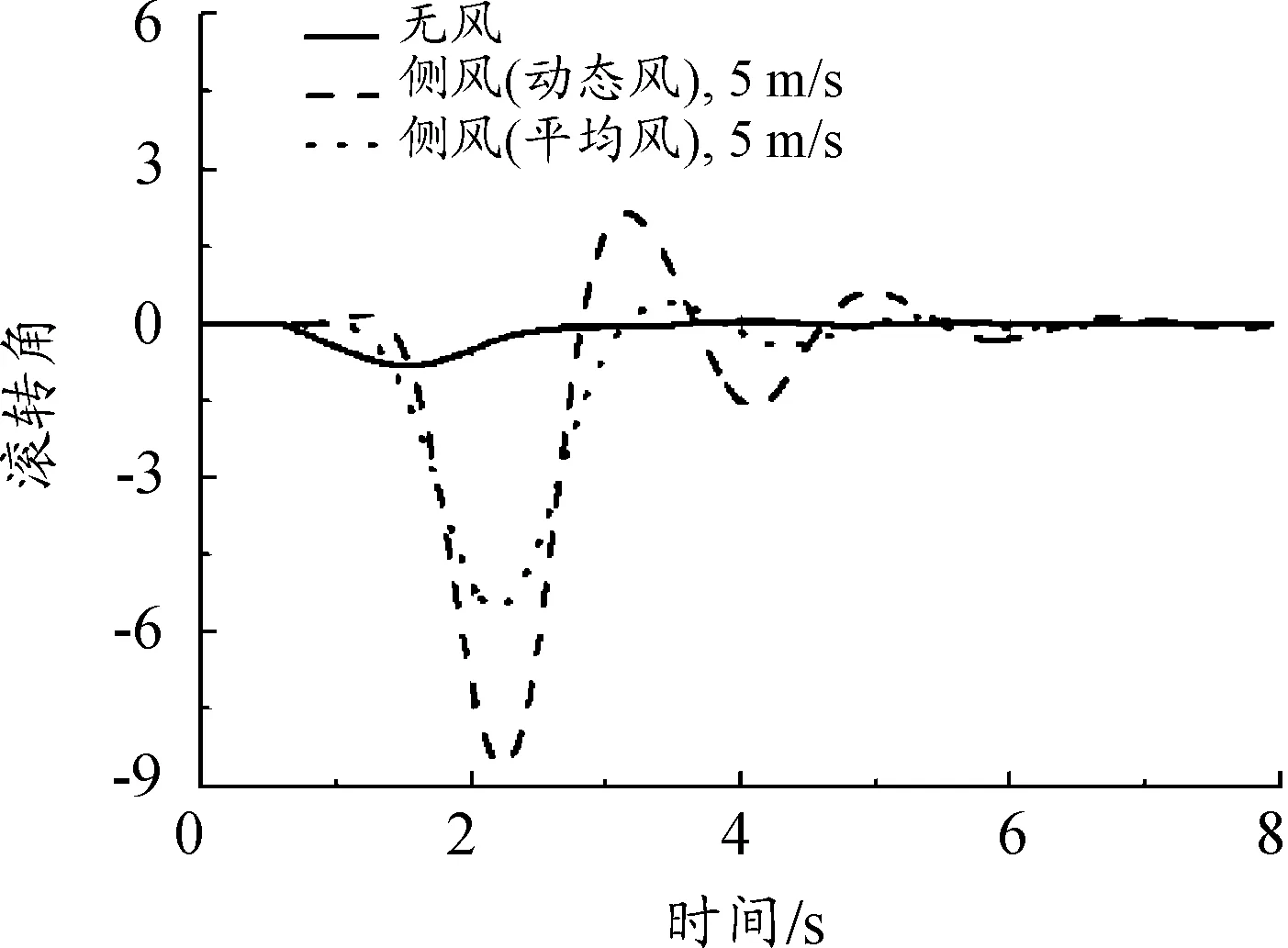
图15 滚转角变化曲线
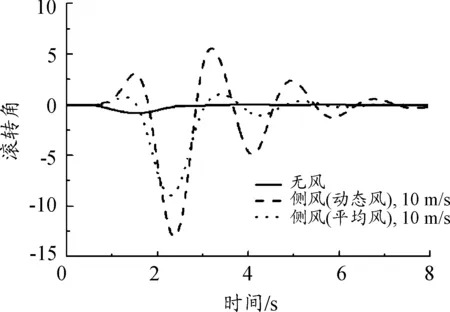
图16 滚转角变化曲线
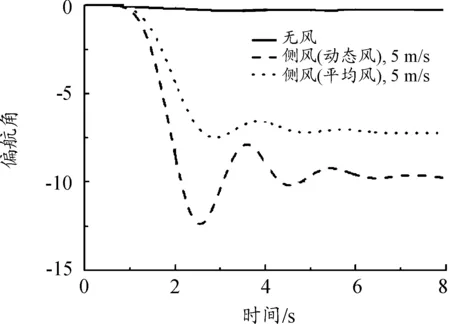
图17 偏航角变化曲线
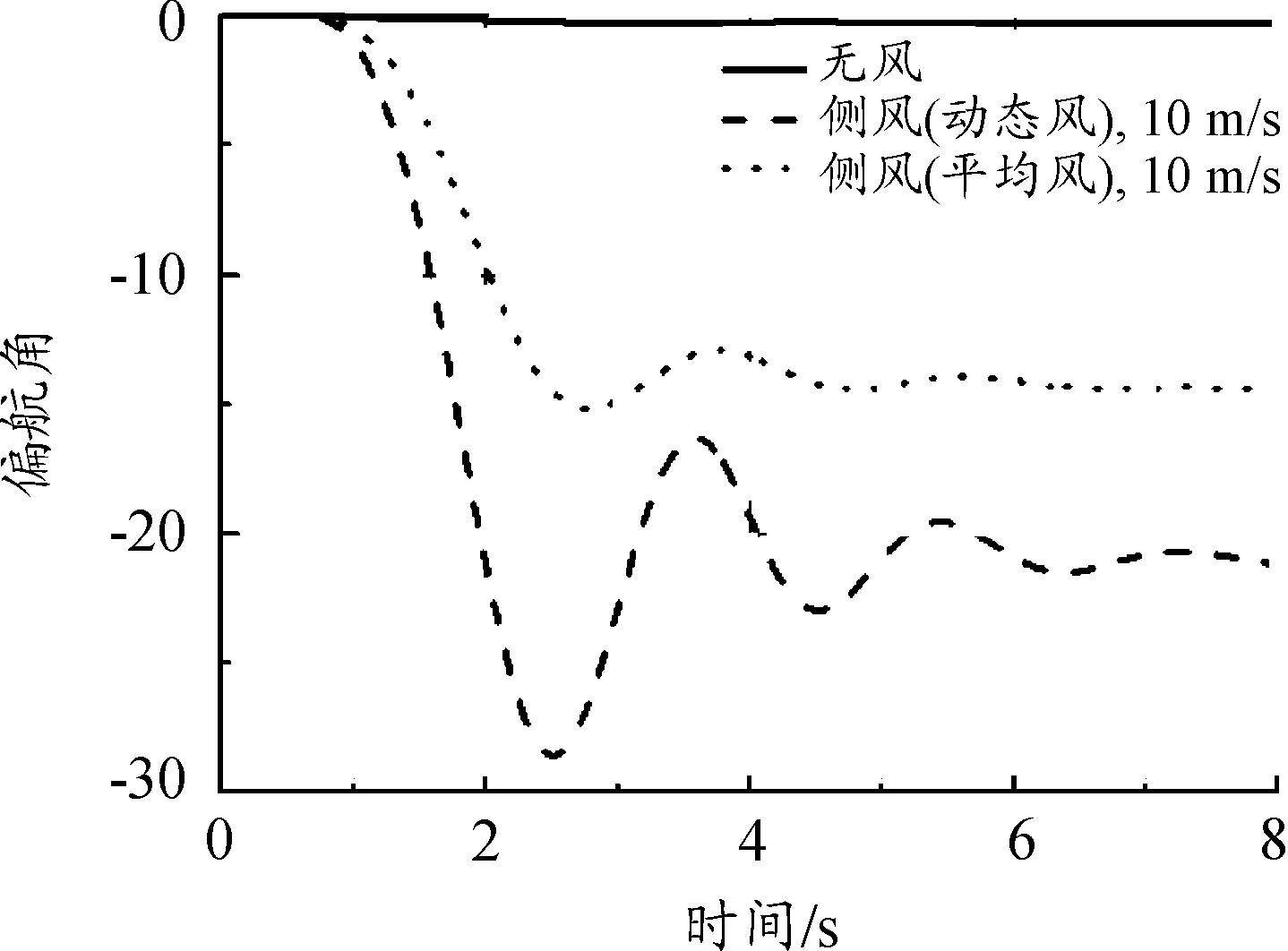
图18 偏航角变化曲线
从结果中可以看出:相比于平均风工况结果,脉动风作用下的无人机滚转与偏航姿态变化幅度增大,侧风(10 m/s脉动风)工况下,无人机的最大滚转角已达到13°、最大偏航角已接近30°,发射安全性明显降低。
4 结论
1) 风速越大,滚转和偏航姿态的变化越剧烈,无人机的发射安全性越低。
2) 迎风发射有助于提高发射安全性,当风速等级较高时,应尽量采用迎风发射;侧风对无人机的侧倾和偏航姿态影响明显,应尽量避免侧风发射。
3) 按照平均风计算得到的发射姿态影响偏小,无人机发射过程中,动态风影响不可忽略。
本文采用的动态风场模拟方法以及在此基础上建立的无人机发射段联合仿真建模方法将为该型无人机的设计和安全性评估提供参考。
