基于动力吸振器的舰炮径筒减振分析

富 威，吴 琼，赵书樊，龚军军，徐芸洁，王美娟

(哈尔滨工程大学 机电工程学院， 哈尔滨 150001)

舰炮是海军水面舰艇上的传统武器，在数次海战中都发挥着极大的作用，当代的国防发展中，舰炮武器更是不可缺少的一部分。舰炮具有自动化程度高、对来袭的目标反应灵活、攻击覆盖面大、持续发射和精确度高等优点，现代的作战平台要求舰炮武器具有功能多样化，打击精确化，武器轻型化，机动作战快速化，指挥控制及平台信息化等特点。在舰炮连续发射的情况下，产生的振动冲击会更加强烈。这种冲击载荷和强烈振动会对舰炮结构造成一定的破坏，影响其稳定性，并且会使其使用寿命缩短。因此，通过对舰炮典型部件的振动特性分析，并对其设置减振系统，是发展和完善我国舰炮的亟需解决的问题。

随着高速傅里叶变换器和在此基础上试验模态分析技术的出现，动力吸振器迎来了一个新的时代。李新兴等[1]分析了吸振原理，重新推导了传统吸振器的优化公式；宋孔杰等[2]对动力吸振器进行了优化设计，主要考虑了吸振器在不同的振动源的作用下的影响；张洪田等[3]设计了一种电磁式吸振器，并且将其应用在船舶用发动机上；邓华夏等[4]用磁流变弹性体替代传统的动力吸振器的弹性体，并且将新型的动力吸振器用移频调谐的方法进行控制，得到了一种更加灵活可靠以及能够调频的动力吸振器。张琳[5]基于动柔度方法中的被动修改法,推导得出附加弹簧质量系统的多自由度系统的动柔度矩阵,并对该多自由度系统中的目标自由度进行零点配置,使该自由度下的相应振动得到抑制。贾富淳[6]为了提升参数型动力吸振器的吸振效果,文中提出一种用于控制杆纵向模态振动的连续参数型悬臂梁动力吸振器。郎军[7]将半主动开关型控制策略应用到接地式动力吸振器中,并进行性能分析和参数优化.首先,利用平均法求得两种半主动接地式动力吸振器的近似解析解,并与相应数值解对比,验证了解析解的正确性与高精度.然后,对两种半主动控制接地式动力吸振器进行参数优化。贺辉雄[8]针对动力吸振器在船舶领域应用较少及舰艇在低频振动时减振降噪措施较难实现这一现状,构建低频线谱激励下舰艇附加动力吸振器设计流程及研究其减振降噪特性。江雄以[9]器件上最大加速度响应有效值最小化为减振设计目标,以吸振器安装位置、尺寸等参数为设计变量,对吸振器进行优化设计,比较了不同材料、不同形式吸振器的减振效果。邢昭阳[10]以Voigt型动力吸振器为基础提出了一种将放大机构应用于含负刚度弹簧元件的动力吸振器模型,对该模型的最优参数进行了研究。苏智伟[11]针对舰船大型机械设备振动冲击隔离对高传递损失减振抗冲元器件的需求,基于负刚度动力吸振机理,构建一种含负刚度(NS)元件的动力吸振器(DVA)混合隔振系统。李强[12]为有效抑制航天设备中由干扰源诱发的低频/超低频振动,提出了一种新型可调动力吸振器(NDVA)。该动力吸振器主要由柔性螺旋弹簧(SFS)及磁性负刚度弹簧(MNSS)组成。付江华[13]设计了动力吸振器多参数优化目标函数,研究人群搜索算法在动力吸振器参数优化中的应用,并运用人群搜索算法、遗传算法和粒子群算法进行仿真计算,对比3种算法对动力吸振器进行参数优化时的稳定性、计算速度、计算精度。王卫峰[14]针对某一特定频率下的振动问题,优化了有阻尼吸振器参数来对其进行吸振。

动力吸振器的设计过程趋于成熟，但是吸振器的参数优化，例如吸振器质量的寻优还没有深入的研究。本文通过研究摇架径筒的受迫振动特性、编写Matlab程序，实现吸振器质量的寻优过程。

1 径筒振动特性分析

对如图1所示的等截面径筒进行分析，忽略其他架体结构的影响，但整体质量不能忽略，在悬臂梁的固定端添加一个集中质量，根据所选目标的实际质量，添加了5 000 kg的集中质量。

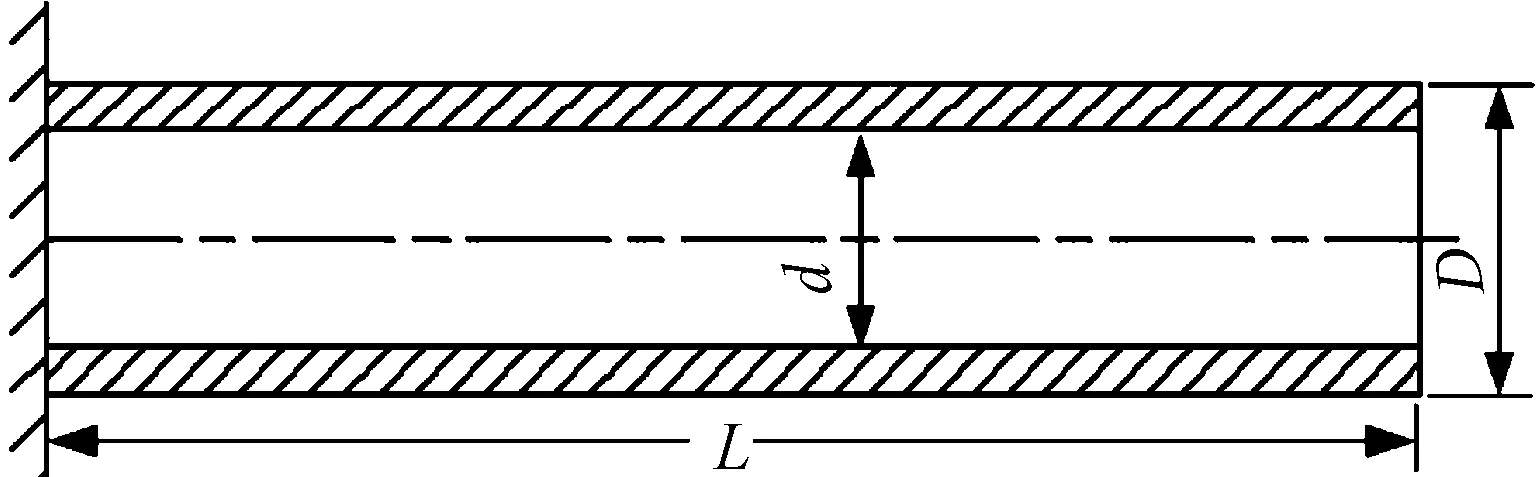
图1 径筒结构简图

径筒结构简化的参数如表1所示。

表1 径筒参数表

1) 径筒横向自由振动方程

根据径筒的简化模型，其横向振动方程可以写为：

(1)

式中：A为径筒的横截面积；E为径筒材料的弹性模量；ρ为密度，径筒的材料均匀，在整个模型中E和ρ为常量，I为径筒的截面惯性矩。假定整个系统具有同频谐振动，则径筒的一般横向振动方程为：

y(x,t)=φ(x)sin(ωt)

(2)

式中：φ(x)表示径筒的振型函数；ω为径筒的圆频率。

整理得到：

(3)

对式(3)进行求解并求导得到：

φ′(x)=C1kcos(kx)-C2ksin(kx)+

C3kch(kx)+C4ksh(kx)

φ″(x)=-C1k2sin(kx)-C2k2cos(kx)+

C3k2sh(kx)+C4k2ch(kx)

φ‴(x)=-C1k3cos(kx)+C2k3sin(kx)+

C3k3ch(kx)+C4k3sh(kx)

(4)

将式(4)中的x用摇架径筒的长度L替换，由于摇架径筒简化为悬臂梁，所以左边的边界条件为挠度y(0)和转角θ(0)为0，另一边的边界条件为弯矩M(L)和剪力Q(L)为0，整理可以得到悬臂梁两个端点的关系式为:

(5)

设：

将边界条件代入式(5)并进行整理，可以得到：

(6)

若使式(6)具有非零解，那么可以推导出：

ch(kL)·cos(kL)+1=0

(7)

此方程是悬臂梁的频率方程，能够解出kL的值，前三阶的值为：k1L=1.875，k2L=4.694，k3L=7.855。摇架径筒的参数为：密度ρ为7 850 kg/m3，弹性模量E为2.1×1011Pa，将k1L的值代回可以得到悬臂梁的一阶横向振动方程。

2) 径筒的横向受迫振动方程

设φ(x)为摇架径筒的横向振动振型函数，则摇架径筒的动能和势能的表达式为：

(8)

式中qi为广义坐标。

在舰炮发射时，摇架受到身管传递过来的载荷，因为这里只分析摇架的径筒，摇架径筒所受到的激励为：幅值为100 000 N，频率为5 Hz，即：

F(t)=100 000sin(10πt)

(9)

在摇架径筒位置的横向位移响应可表示为可表示为：

y(x,t)=∑iφi(x)qi(t)

(10)

由虚位移原理推导得到广义力表达式为：

(11)

Lagrange方程为：

(12)

联立式(8)、式(12)，在系统不同的广义坐标下进行求解，得到：

(13)

广义质量与广义刚度的表达式为：

(14)

由式(12)、式(13)以及式(14)可以得到运动微分方程，写成矩阵形式为：

(15)

可以写成：

(16)

编写MATLAB程序，得到摇架径筒上各点的响应，并且使用ANSYS/Mechaincal APDL软件，用有限元法再次计算摇架径筒上各点的响应，理论计算值与有限元法计算结果如图2所示。

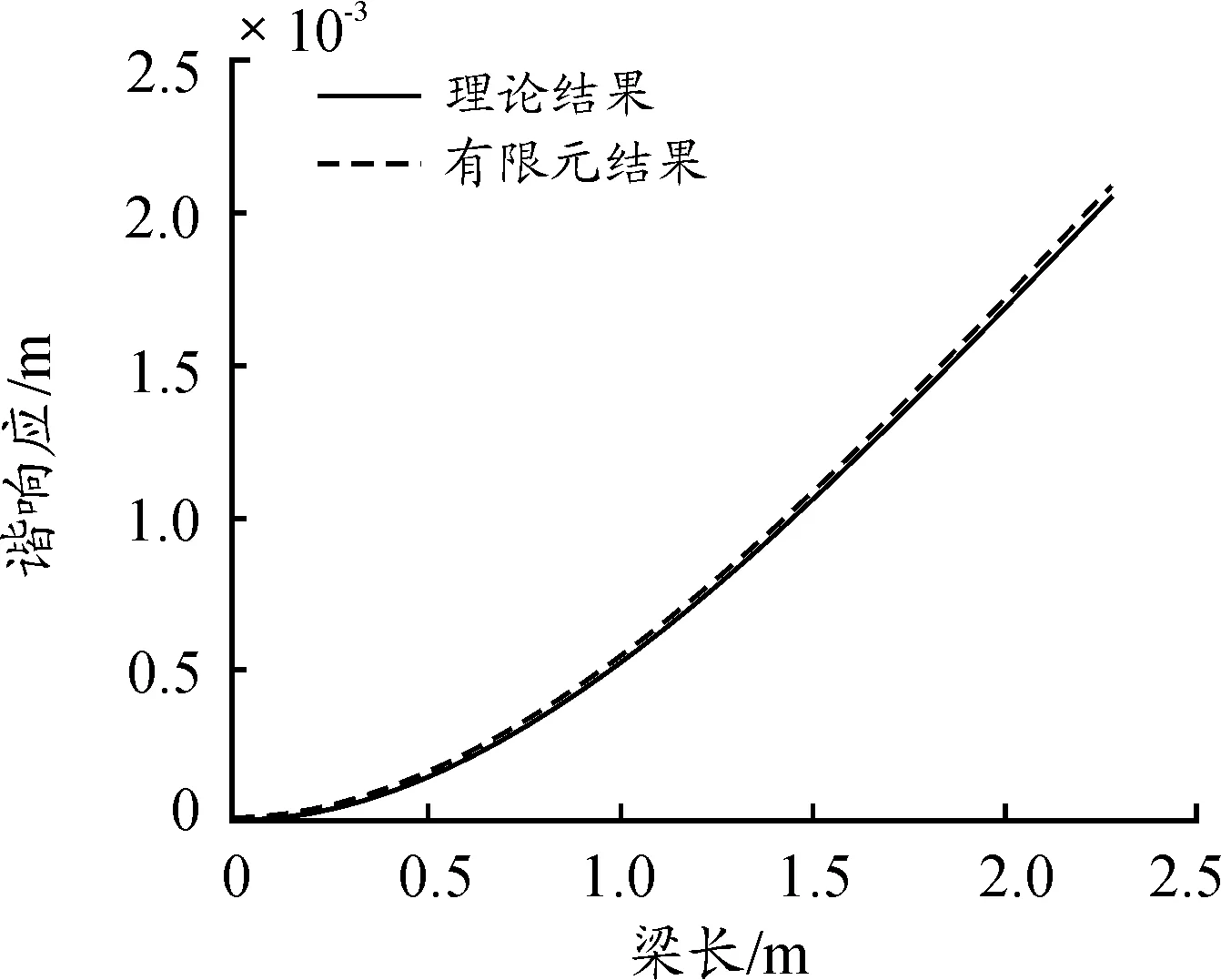
图2 径筒上各点的响应曲线

根据图2所示，当摇架径筒上不加吸振器时，由理论计算得到的结果与有限元分析结果基本一致，证明利用振动方程求出动能和势能后代入第二拉格朗日方程求解不加吸振器时摇架径筒上各点的响应的方法是正确的。

2 带有吸振器的径筒振动特性分析

本文选用被动式吸振器，具有较高的精度，相比于其他的动力吸振器，被动式吸振器具有结构简单，吸振性能稳定等特点，降低了生产成本。在径筒上安装一个被动式吸振器来使其振动减小，其中mx-kx-cx组成的系统为吸振器的理论结构，结构简图如图3。

图3 带有吸振器的径筒结构简图

设x0为吸振器在径筒上的安装位置，mx表示吸振器的总质量，kx表示吸振器的刚度，ξ表示吸振器的位移，cx表示吸振器的阻尼。将吸振器安装在径筒上后的系统的动能和势能表达式为：

(17)

将式(17)代入到第二拉格朗日方程中，可以得到：

(18)

(19)

加入吸振器后广义质量和广义刚度的表达式为：

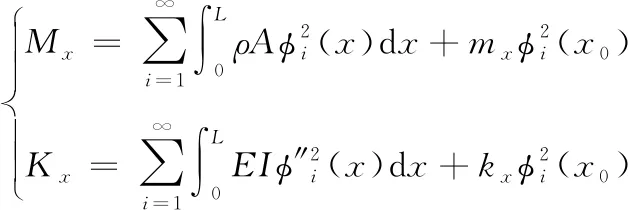
(20)

使用模态叠加法，设目标部件的响应求解位置为LR，可以求解该位置的受迫响应为：

(21)

将吸振器的质量设置为1 kg，编写相应的MATLAB程序，安装在径筒的自由端，求出带有吸振器的径筒上的各点响应，同时，使用ANSYS/Mechaincal APDL软件，用有限元法求解加入吸振器后径筒的响应与计算理论结果如图4所示。

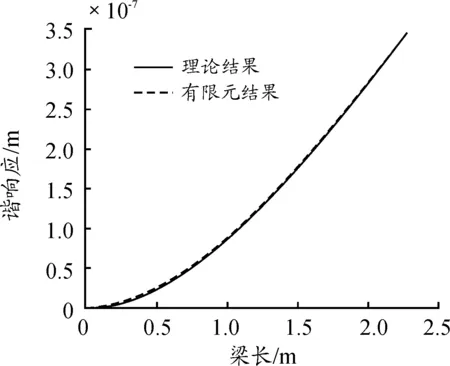
图4 带有吸振器的径筒上各点的响应曲线

根据图4所示，当径筒上安装吸振器时，理论计算得到的结果与有限元分析结果基本一致，证明利用振动方程求出动能和势能，然后将其代入第二拉格朗日方程求解安装吸振器的径筒上各点的响应的方法是正确的。

3 动力吸振器优化设计

动力吸振器的设计受多方面的制约，改变某一个参数时，对动力吸振器的吸振效果都会产生很大的影响。动力吸振器性能的好坏受到在待减振系统中的吸振器的阻尼/吸振器的质量比的影响。为了将吸振器的性能达到最优，设计人员在进行动力吸振器的设计时，必须要考虑质量方面的作用。

动力吸振器的吸振效果的好坏与吸振器的质量有关，因此在本节中对吸振器的质量进行寻优。在径筒上安装动力吸振器，动力吸振器的安装位置保持不变。设置吸振器的刚度为986.96 N/m，设动力吸振器的形式为粘性阻尼，设置阻尼比大小为0.002。

动力吸振器质量的不同会直接导致响应情况的不同。计算在径筒受到幅值大小为100 000 N，频率为5 Hz外界激振力作用时的受迫响应。将动力吸振器的安装位置保持不变，改变动力吸振器的质量，分析径筒自由端的响应情况。利用Matlab软件编写将吸振器安装在自由端时，质量寻优的程序。

经过计算得到动力吸振器质量不同时径筒自由端的响应曲线如图5所示。

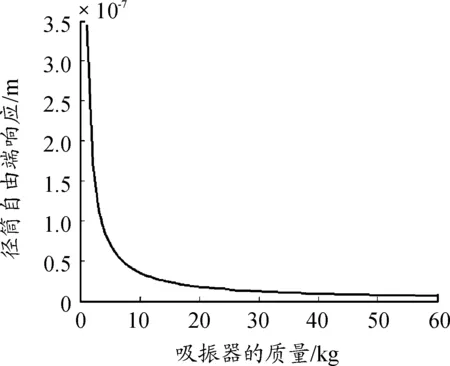
图5 动力吸振器质量不同时径筒自由端的响应曲线

通过图5可以看出，动力吸振器的质量对吸振器的吸振效果有很大的影响。当保持吸振器的安装位置不变时，随着吸振器质量的增大，径筒自由端的振动幅值越小。当吸振器的质量在0～10 kg时，随着质量的增大，径筒自由端的振动幅值迅速变小；当动力吸振器的质量大于等于15 kg时，径筒自由端的振动幅值减小的幅度不在那么明显。综合上述分析可以得到：动力吸振器的质量虽然能够对吸振效果影响明显，但是吸振器的质量不是越大越好，当吸振器的质量达到一定数值时，吸振器的效果不在那么明显。因此合理选择动力吸振器的质量，不但可以达到对径筒减振的效果，还会减轻径筒的整体质量，减少动力吸振器的制造成本。

从图6可以看出，动力吸振器的质量一定时，径筒上各处位置越靠近炮筒的自由端，振动幅值越大。动力吸振器的质量在大于等于15 kg时，径筒上各点的振动幅值基本相同。因此可以得出相同的结论：在动力吸振器的质量不是越大越好，合理选择动力吸振器的质量，不但可以达到对径筒减振的效果，还会减轻径筒的整体质量，减少动力吸振器的制造成本。

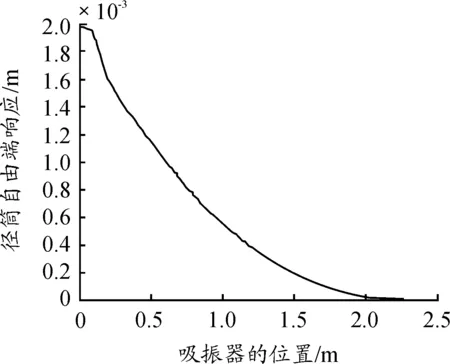
图6 动力吸振器安装位置不同时径筒自由端响应曲线

综上所述，动力吸振器应该安装在径筒的自由端，质量为15 kg，刚度为14 804.4 N/m，阻尼比大小为0.002，此时，吸振效果达到最好。

4 结论

本文分析了动力吸振器的影响因素，对动力吸振器的安装位置和质量进行优化设计，了解安装位置和质量对动力吸振器吸振效果影响的规律：在动力吸振器的安装位置不影响径筒正常运作的前提下，动力吸振器的安装位置越靠近径筒的自由端，吸振效果越好；动力吸振器质量增大，径筒自由端的振动幅值减小，但动力吸振器的质量不是越大越好，合理选择动力吸振器的质量，可对径筒减振，减少动力吸振器的制造成本。