基于粒子滤波的非线性退化设备剩余寿命自适应预测
2020-11-05胡昌华张建勋
王 玺,周 薇,胡昌华,张建勋,裴 洪,刘 轩
(1.海装驻北京地区第一军事代表室, 北京 100076; 2.战略支援部队某部, 北京 102209; 3.火箭军工程大学导弹工程学院, 西安 710025)
随着现代科学技术的飞速发展,复杂性已经成为工程设备的一个重要发展趋势[1]。然而,由于外部环境和内部因素的相互作用,工程设备的性能会随着运行的时间而逐渐产生退化,并在达到某种量级时,导致设备的失效。如果不能准确掌握设备的健康状态,在运行中一旦发生突发失效,可能会对社会安全和人身财产造成难以预计的后果。因此,针对设备的退化特性,建立相应的退化模型,进而由监测的退化数据实现对退化设备的剩余寿命(remaining useful life,RUL)预测是目前可靠性领域的一项研究热门。
目前,基于退化建模的剩余寿命预测方法已经成功的应用在激光器[2]、陀螺仪[3-4]、综合传动装置[5-6]等领域。例如,文献[2]建立了同时考虑测量误差和随机效应的退化模型,利用经典Kalman滤波理论实现了激光器的剩余寿命预测。文献[3]同样地考虑了随机效应对陀螺仪剩余寿命预测的影响,并且基于多组同类型陀螺仪的历史退化数据实现了模型的参数估计。文献[5]在退化建模中考虑了监测数据的测量不确定性,进一步提高了综合传动装置的剩余寿命预测精度。
根据现有文献可知,工程设备在性能退化过程中普遍存在着个体差异不确定性和非线性[7-14]。其中,个体差异不确定性又称为随机效应,是指由于受到不同的外力影响,同类型退化设备在性能退化过程中存在的退化差异。因此,有必要在退化建模中充分地考虑个体差异不确定性对剩余寿命预测的影响。为此,文献[10-12]展开了相关的研究工作,基于Wiener过程进行退化建模,并将模型中的漂移系数作为随机参数,用以描述个体差异不确定性。通过利用经典Kalman滤波理论实现了退化设备的剩余寿命预测,并且证明了考虑个体差异不确定性和非线性可以有效地提高剩余寿命预测的精度。但是,大多数相关工作在参数估计中通常假定存在多组同类型设备的历史退化数据,致使剩余寿命预测的精度受限于数据量[2,5-9,11,14]。然而,在实际中经常会遇到缺乏此类历史退化数据的情况,如陀螺仪、综合传动装置、航空发动机等,造价昂贵且数量少,工程上难以通过大量设备进行寿命试验[6]。因此,以上方法具有一定的局限性,且目前相关的研究工作较少。
鉴于此,本文基于非线性Wiener过程建立了具有双隐含状态的随机退化模型,并利用粒子滤波算法实现了对隐含状态的实时估计,克服了经典Kalman滤波理论的限制,进而在首达时间的概念下推导出了剩余寿命的分布。针对缺乏历史退化数据和先验信息等问题,提出了一种基于粒子期望最大化(particle expectation maximization,PEM)算法的参数估计方法,实现了模型参数的自适应估计和剩余寿命分布的在线更新。最后,通过某型陀螺仪的实际退化数据验证了本文方法的有效性和优越性。
1 模型描述
考虑采用具有一般性的非线性Wiener过程来描述复杂退化设备的随机退化过程{X(t),t≥0}。具体地,{X(t),t≥0由标准布朗运动(standard Brownian motion,SBM)驱动,表示为:
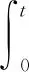
(1)
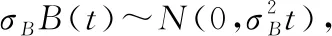
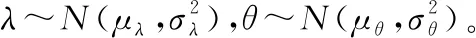
基于首达时间(first hitting time,FHT)的概念[9-15],认为退化过程{X(t),t≥0} 首次穿过设定的失效阈值ω时,设备的寿命终止。因此,将设备的寿命T定义为:
T=inf{t∶X(t)≥ω|X(0)<ω}
(2)
式(2)中:inf表示求集合的下确界,即首达时间;ω为预先设定的失效阈值,一般由工业标准确定。
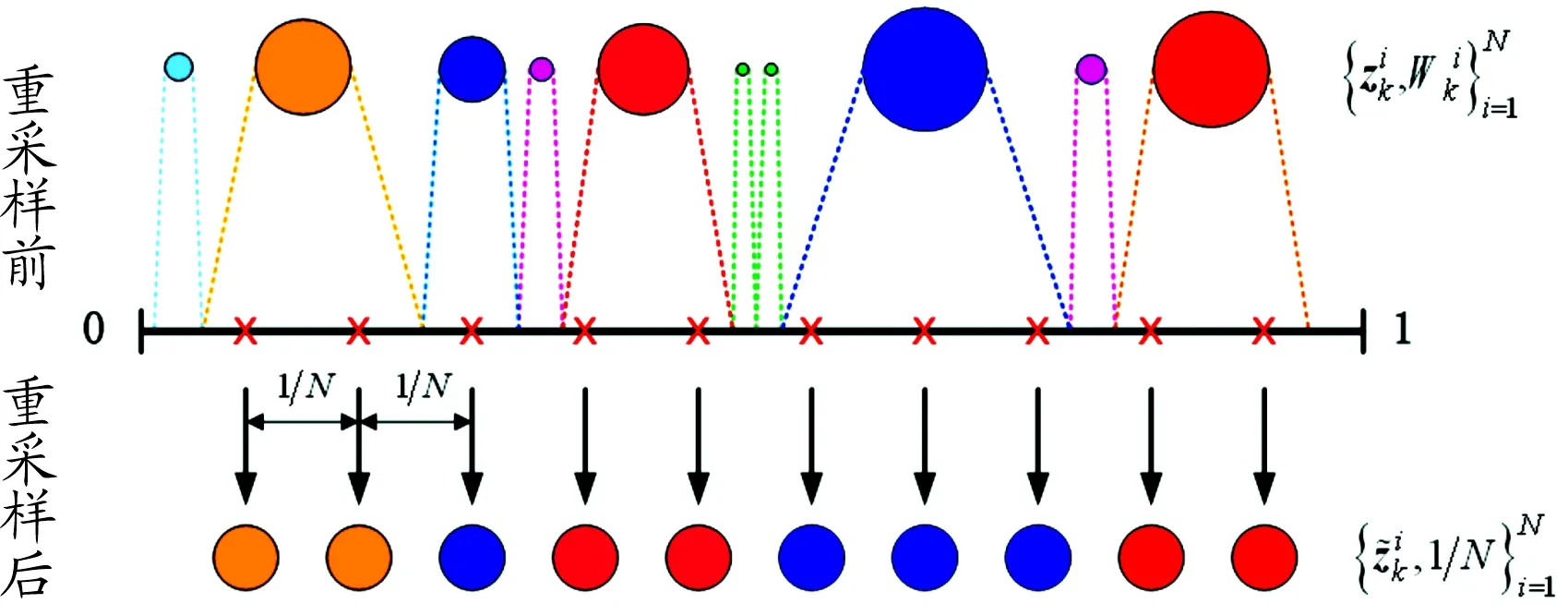
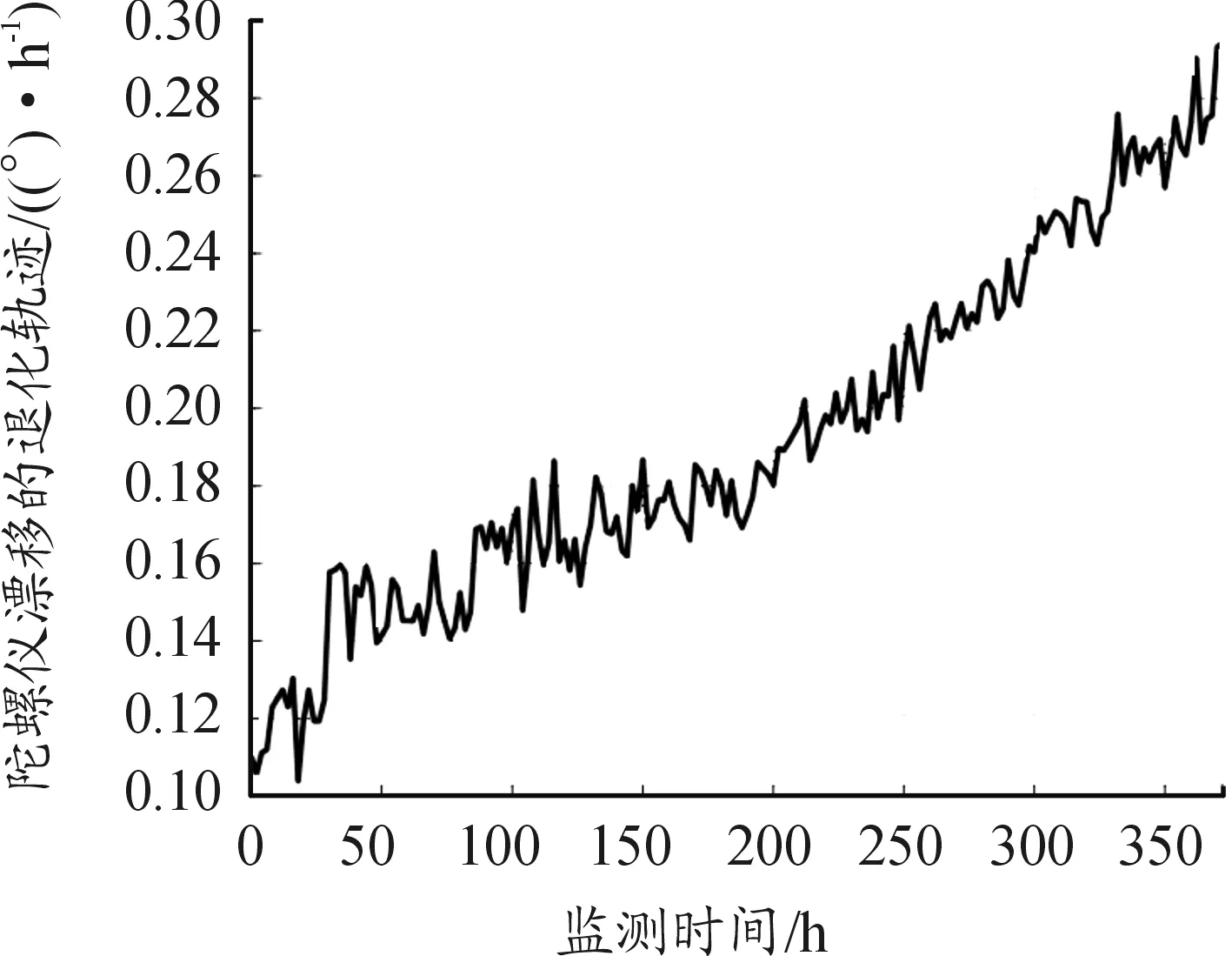
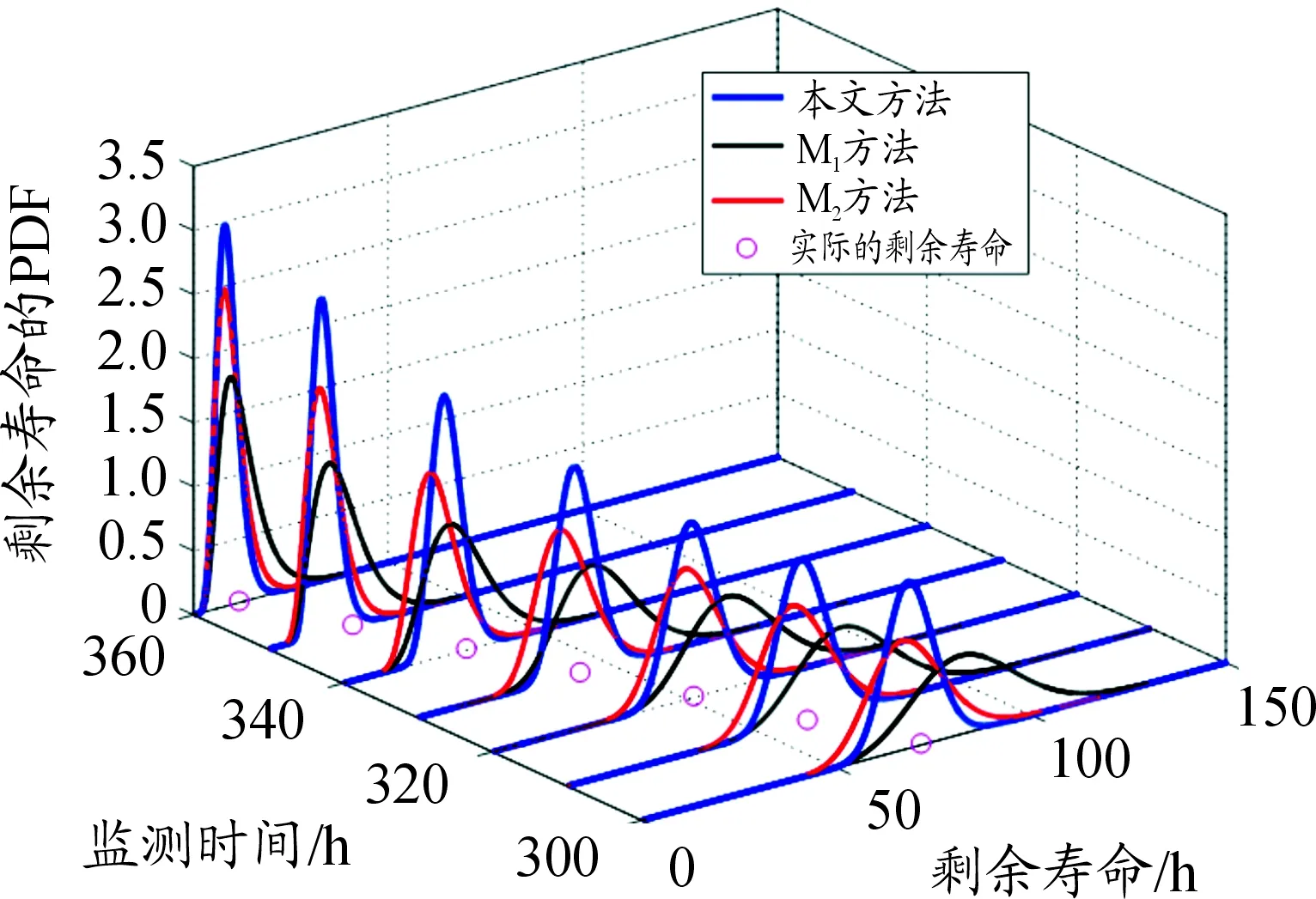
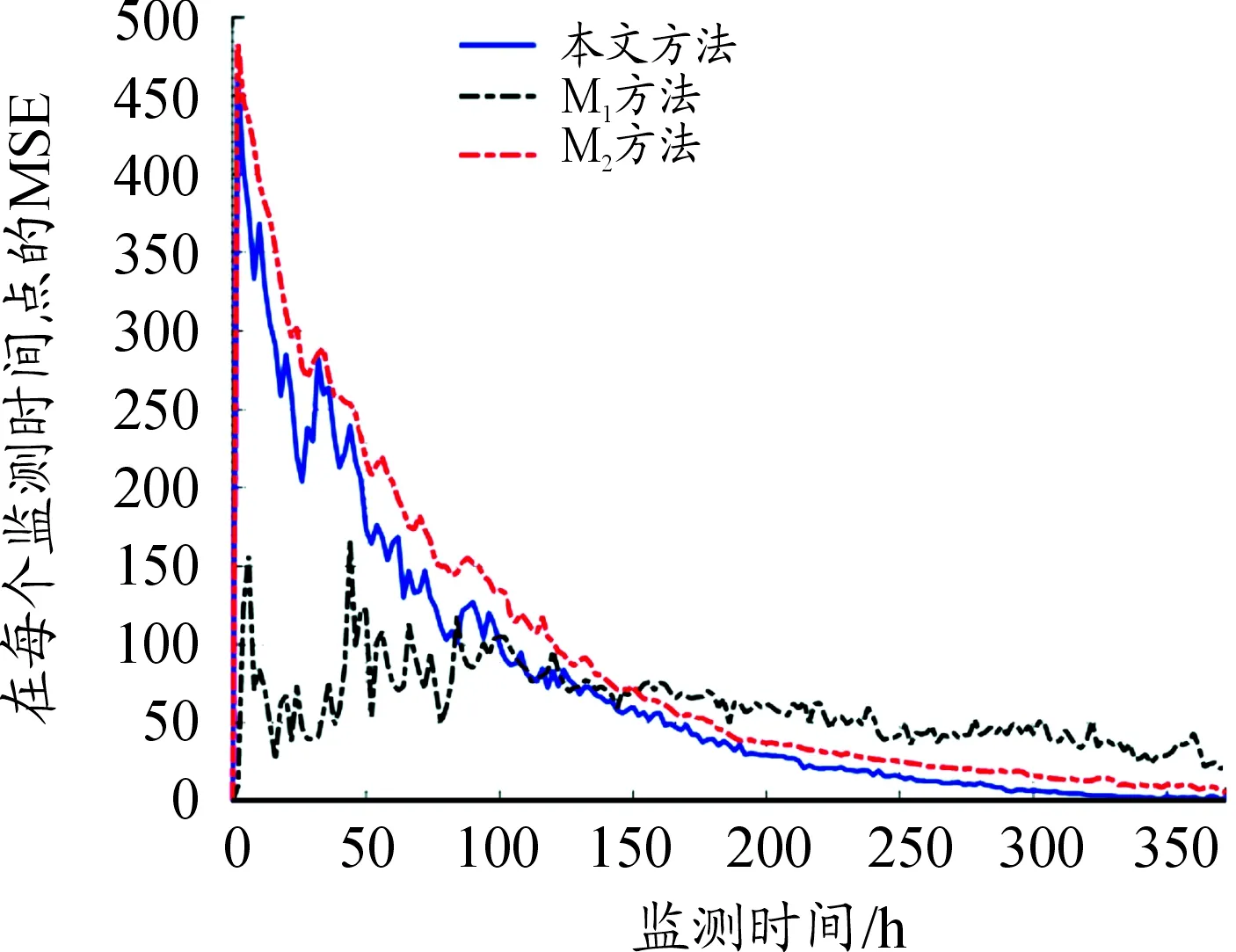
在以上的框架下,假定在离散时刻点0=t0 Lk=inf{lk>0∶X(lk+tk)≥ω}〗 (3) (4) (5) (6) (7) (8) 然而,在执行PF算法时会遇到一个严重的粒子退化现象,即随着迭代次数的增加,只有少量粒子的重要性权重比较大,大部分粒子的重要性权重很小。因此,粒子重要性权重的方差随着运行时间不断增大,状态空间中的有效粒子数较少,使得大部分计算时间浪费在更新重要性权重小的粒子上,造成估计性能的下降[19-20]。为了衡量粒子的退化程度,引入有效抽样尺度,定义为: (9) 式(9)中:Neff越小,意味着粒子退化现象越严重。通常,抑制粒子退化的重要手段是利用重采样算法,通过对粒子的重新采样,剔除重要性权重小的粒子,“繁殖”重要性权重大的粒子,从而降低粒子退化现象。一般,设定重采样阈值为Nth,当Neff 图1 重采样的示意图 (10) 下面,将基于双隐含状态的后验分布,实现退化设备的剩余寿命预测。 根据式(3)中定义的剩余寿命,在考虑个体差异不确定性的情况下,剩余寿命的PDF可以计算如下: fLk|Θ,X1∶k(lk|Θ,X1∶k)=Ezk|Θ,X1∶k[fLk|zk,Θ,X1∶k(lk|zk,Θ,X1∶k)] (11) 式(11)中:Ezk|Θ,X1∶k[·]是在给定模型参数向量Θ和退化数据X1∶k的条件下,关于zk的条件数学期望算子。 为了计算式(11),首先给出以下结果[16]。 (12) 基于PF算法,联合式(11)和式(12),在tk时刻预测退化设备的剩余寿命的PDF可以近似计算为: (13) 基于以上结果,在获得新的退化数据后,可以通过式(13)预测退化设备的剩余寿命。但需要注意的是,上述结果是在模型参数向量Θ给定的条件下推导的,因此必须先对模型参数向量Θ进行参数估计。然而,现有大多数相关工作存在着一个共性问题,即假定存在多组同类型设备的历史退化数据,基于极大似然方法离线地估计出模型参数,并且这些参数一旦确定,就不再随着新的退化数据进行在线更新[2,5-9,11,14]。此外,在实际中经常会遇到缺乏此类历史退化数据的情况,例如新列装的武器装备、新型工程设备等。鉴于此,本文提出了一种基于PEM算法的参数估计方法,利用实时监测的退化数据来实现模型参数的自适应估计和剩余寿命分布的在线更新,使得预测的剩余寿命更加准确,有利于掌握退化设备的健康状态。 根据极大似然估计(maximum likelihood estimation,MLE)理论,由于随机参数λk和θk为双隐含状态,因此需要基于可观测的退化数据X1∶k来估计出模型参数向量Θ。这里,自然可以采用一种广泛应用于缺失或不完全数据条件下的EM算法来实现模型的参数估计。EM算法是通过最大化联合似然函数p(zk,X1∶k|Θ)去逼近模型参数的MLE,具体过程通过迭代以下两步来实现。 E步: (14) M步: (15) 首先,基于贝叶斯定理和建立的退化模型(4),E步中的对数联合似然函数可以通过式(16)形式进行计算,即: lnp(zk,X1∶k|Θ)=lnp(X1∶k|zk,Θ)+lnp(zk|Θ)= (16) 然后,通过E步对式(16)求条件数学期望,有: (17) 式(17)中: (19) p(zm|Θ,X1∶k)=p(zm|Θ,X1∶m)× (20) (21) 因此,基于式(20)和式(21),可以得到: (22) 到此,基于PS算法解决了非线性平滑问题。下面,将给出本文所提出的PEM算法的具体实现过程。 基于PS算法,可以直接得到式(17)中的Λ1和Λ3,结果如下: (23) (24) (25) (26) 式(26)中: (27) 基于以上的结果,可以将本文所提出的剩余寿命自适应预测方法归纳如下: (3) M步。根据式(26)和式(27),计算 如果无法给出解析解,则通过搜索算法进行求解。 (4) 迭代。如果EM算法已经收敛,则终止此步骤,否则令q=q+1,并返回步骤(2)。 (5) 剩余寿命预测。 ② 基于式(5),在tk时刻预测退化设备的剩余寿命的PDF可以由式(13)计算。 由此可见,本文所提出的剩余寿命自适应预测方法,可以利用每一个退化数据对模型参数进行自适应地估计,进而实现剩余寿命分布的在线更新,克服了非线性退化设备缺乏历史退化数据和先验信息的问题,这对工程实际具有重要意义。 固定在惯性平台上的陀螺仪是航空航天及导弹武器系统的关键部件,其工作性能直接影响了导航的精度。当惯性平台工作时,陀螺仪的转子高速旋转势必会造成旋转轴机械磨损,随着磨损的积累,表现为漂移系数增大,最终导致设备失效。而且对于安装在惯性平台上的陀螺仪,数量少且测试成本高,一旦发生失效,所造成的后果将难以估计。因此,准确估计陀螺仪的剩余寿命,对提高整个系统的安全性和可靠性至关重要。 下面通过某型陀螺仪在实际使用中监测的退化数据来验证本文方法的有效性。如图2所示,在实验中该型陀螺仪根据技术指标,设定失效阈值ω=0.3(°/h),每隔2 h监测一次,直到372 h为止,共监测了187次。这里,选择以下幂函数形式的随机退化模型进行建模,即: X(t)=X(0)+λ·tθ+σBB(t) (28) 到目前为止,此类模型已经在陀螺仪、航天发动机、锂电池等复杂设备的退化建模中得到了广泛的应用[8-13]。 图2 陀螺仪漂移的退化轨迹 从图2中可以看出,随着监测时间的增加,陀螺仪的漂移系数整体呈上升趋势。基于该陀螺仪的实际退化数据,应用所提出的PEM算法可以实现模型参数的自适应估计,结果如图3所示。从图3中可以看出,所提方法可以在每一个退化数据可用时估计模型的参数,而且估计的模型参数会随着退化数据的积累快速收敛。 为了进一步验证本文方法的有效性和优越性,选择文献[11]和文献[12]中的方法进行对比研究。 1) M1:假定存在多组同类型设备的历史退化数据,基于极大似然的方法离线地估计出模型参数,并且这些参数一旦确定,就不再随着新的退化数据进行更新[11]。 2) M2:在退化建模中忽略了非线性函数中参数的随机性,利用经典的Kalman滤波理论实现了漂移系数的实时估计,并且在新的退化数据可用时,可以实现模型参数的自适应估计和剩余寿命分布的在线更新[12]。 图3 模型参数的自适应估计曲线 在实验中,为了验证本文方法可以有效地应用于缺乏先验信息的退化设备,进行如下设定:本文方法和M2方法选用随机的模型初始参数,而M1方法选用合适的模型初始参数。图4给出了三种方法在监测时间300~360 h时,每隔5个监测时间点预测的剩余寿命的PDF对比图。从图4中可以看出,三种方法预测的剩余寿命的PDF曲线均覆盖了实际的剩余寿命,并且随着监测时间的增加,PDF曲线愈来愈尖锐,这意味着预测的剩余寿命结果愈来愈准确,不确定性愈来愈低。此外,由于本文方法考虑了非线性函数中参数的随机性,并且在每一个监测时间点都可以实现模型参数的自适应估计和剩余寿命分布的在线更新,因此本文方法得到的PDF曲线更加尖锐,说明预测的不确定性更低,相比之下具有更好的预测性能。 图4 三种方法预测的剩余寿命的PDF曲线 为了进一步量化剩余寿命预测的精度,引入可靠性领域中常用的均方误差(mean square error,MSE)指标,该指标同时考虑了剩余寿命预测的精度和不确定性,因此在剩余寿命预测中被广泛应用。具体地,在tk时刻的定义式如下: (29) 图5给出了三种方法在所有监测时间点的MSE结果。从图5中可以看出,由于本文方法和M2方法选用随机的模型初始参数,因此在监测初期退化数据较少时,得到的结果并不理想。但是,随着监测时间的增加,退化数据的积累,本文方法的MSE明显低于M1方法和M2方法,说明本文方法在预测剩余寿命的性能上具有明显的优势。 图5 三种方法在所有监测时间点的MSE曲线 以上的实验结果表明,本文方法可以显著地提高剩余寿命预测的精度,降低预测的不确定性,在实际应用中具有更好的预测性能,并且更加适应于缺乏历史退化数据和先验信息的非线性退化设备。 1) 本文在状态空间模型的框架下建立了具有双隐含状态的非线性随机退化模型,并且在经典Kalman滤波理论不适用的情况下,基于粒子滤波算法实现了对双隐含状态的实时估计。 2) 基于粒子滤波算法,在首达时间的概念下推导出了剩余寿命的分布,并且在获得新的退化数据时,可以实现剩余寿命分布的在线更新。 3) 提出了一种基于PEM算法的参数自适应估计方法,克服了非线性退化设备缺乏历史退化数据和先验信息的问题,实现了模型参数的自适应估计。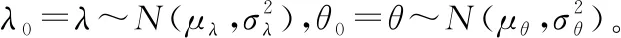

2 基于粒子滤波的剩余寿命预测
2.1 基于PF的双隐含状态估计
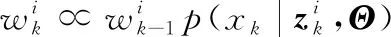

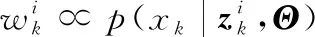
2.2 考虑个体差异不确定性的剩余寿命预测
3 基于PEM算法的自适应参数估计
3.1 总体框架
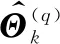
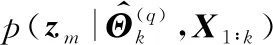
3.2 基于粒子平滑的双隐含状态平滑
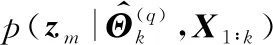
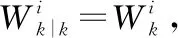
3.3 基于PEM算法的实现过程
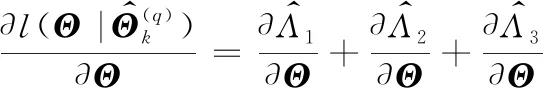

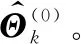
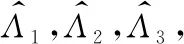

4 实例验证

5 结论
