基于可靠度理论的阻滑键加固渣土边坡多目标优化设计方法

王 盈，曾江波，姚文敏，李长冬

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.深圳市勘察测绘院有限公司，广东 深圳 518028)

0 引言

现代城市建设过程中，由地铁等工程大量开挖施工产生的弃土，经运输堆填形成了大量的渣土余泥边坡。这类边坡主要由物理力学性质较差、不均匀性强的废弃余泥渣土堆积而成，在不利因素作用下容易产生失稳，严重威胁城市居民点和交通的安全。如2015年深圳市光明新区红坳余泥渣土临时受纳场发生的“12·20”滑坡事故，造成77人遇难，直接经济损失达8.81亿元[1]。为此，渣土边坡的稳定性评价与防控研究引起了社会各界的高度关注[2]。

边坡加固的措施有多种，其中阻滑键在工程实践中得到了较广泛的应用。针对在滑体较为深厚、滑动面明确且常规支护方法耗资大的滑坡防治工程，多采用阻滑键结构进行加固[3-4]。阻滑键结构通过置换滑带土体并增强滑带土体力学强度，从而提高边坡的整体稳定性。郑轩[4]等将常规的抗滑桩和阻滑键连接成整体，形成连续桩键结构用于三峡水库猴子石滑坡防治，现场监测结果表明该结构阻滑效果显著。阻滑键加固边坡施工时，一般需先确定滑面位置，然后开挖坡体形成竖井或者平洞，再回填钢筋混凝土材料，因此其工程量较大，施工费用较高[3]。对于人工堆填形成的渣土边坡在堆填过程中预埋阻滑键结构，不仅可提高渣土边坡的整体稳定性，还可显著降低开挖和支护的工程量及难度。

传统阻滑键结构多采用确定性设计，依据专家经验或者局部试验获得岩土体参数从而确定边坡安全系数和阻滑键的埋设长度和位置等[3-4]。在实际现场试验中由于场地条件复杂和试验条件的限制，较难获取到岩土体参数的确定数值和精准统计规律。然而，为了保证边坡整体稳定而忽略参数的不确定性时，容易造成过度设计[5]。可靠度设计可以通过调整易控的设计参数，降低整体系统中由于岩土体参数等不可控因素的变异性造成的设计结果不确定性，确保设计方案安全可行[6-7]。

滑坡的预估破坏损失关系着滑坡灾害的影响程度和范围，是衡量支护结构加固效果和边坡稳定安全的重要指标。滑坡的预估破坏损失主要指考虑概率分析条件，未来不同破坏强度的滑坡灾害造成承灾体价值损失而引起的预估经济损失[8-9]。目前对于挡土墙、锚杆及抗滑桩等支挡结构可靠度设计中，多着重于设计结构的安全和使用性能[10-11]，较少关注滑坡的预估破坏损失对结构设计的影响。

由于余泥渣土的疏散性和人工分层的特点，渣土边坡土体参数的不确定性相比天然斜坡更为复杂。当前，渣土边坡的加固与防控研究主要借鉴传统滑坡防治经验，对实际岩土体的不确定性考虑不足。因此，本文基于岩土工程的可靠度设计方法，考虑渣土边坡岩土体参数的不确定性和预估破坏损失，采用多目标优化设计，提出预埋阻滑键结构加固渣土边坡的优化设计方法。以深圳市某渣土边坡为例，进一步阐述多目标优化设计过程，并进行阻滑键布设参数对加固效果的影响分析。研究成果可为类似渣土边坡防控提供一定的借鉴与参考。

1 阻滑键加固渣土边坡稳定性分析方法

人工堆填的余泥渣土较为松散，黏聚力较差，与原有土层分层特性显著，在降雨等不利因素影响下容易发生渣土堆积体与山体接触面的滑动破坏[12]，渣土边坡的防控研究需选用适当的边坡稳定性评价分析方法。边坡稳定性评价方法多采用极限平衡法，主要包括Bishop法、Janbu法和Morgenstern-Price法和Spencer法。本文在阻滑键加固渣土边坡的稳定性分析中，主要采用Geo-Studio软件的Slope/W模块的Bishop法对渣土边坡岩土体进行条分，结合滑面自动搜索方法确定渣土边坡的最危险滑动面并计算其稳定性系数[13]，据此计算阻滑键沿最危险滑动面布设加固的渣土边坡稳定性系数，如图1所示。采用Bishop法，渣土边坡极限平衡状态时的稳定性系数的求解公式为可表述为[14]：

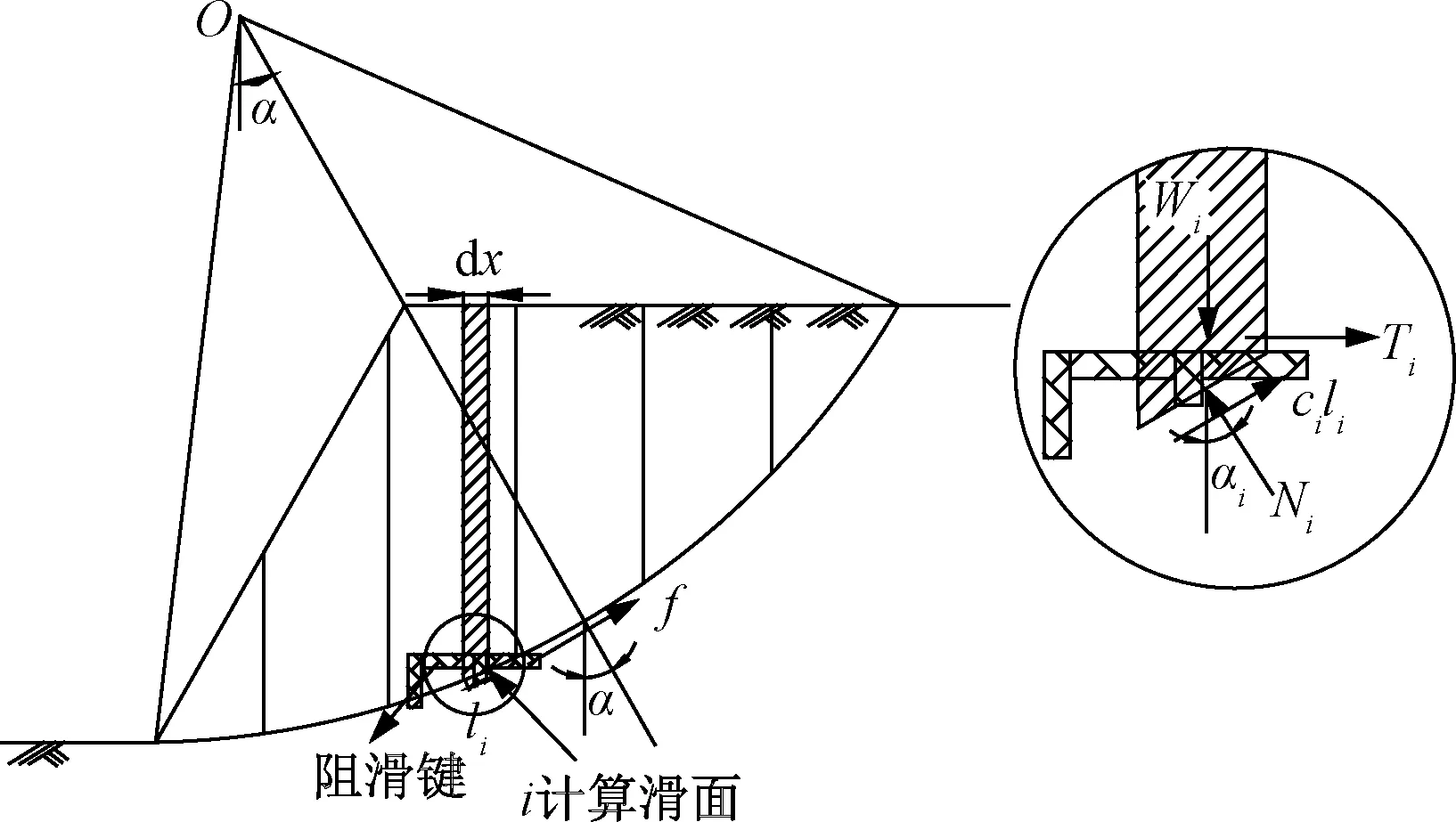
图1 阻滑键加固边坡稳定性分析条分法示意图 (据周汉荣[14]，有修改)Fig.1 Schematic diagram of slope stability analysis[14]

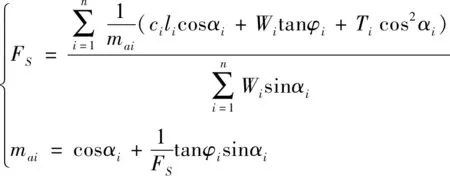
(1)

式中：ci——第i个土条的黏聚力；

li——第i个土条的滑弧长度；

Wi——第i个土条的重力；

φi——第i个土条的内摩擦角；

αi——第i个土条的底面中点的法线与竖线的夹角；

Ti——第i个土条上阻滑键提供的抗滑力，无阻滑键布设时Ti=0。

2 理论模型

在边坡加固设计中，通常以加固效果和工程造价作为设计中的重点考虑因素，以期实现加固效果最大化和工程造价最小化的双重目标。实际上加固效果和工程造价往往存在一定的矛盾，通常较好的加固效果需要较高的工程造价才得以实现。此外，实际工程设计中潜在的预估破坏损失也是需要提前考虑的因素，而较好的加固效果也意味着较低的预估破坏损失。因此，边坡加固工程设计是一个典型的多目标优化设计问题。

本文基于可靠度理论进行多目标优化设计主要考虑三个方面，即选择设计可控参数、不可控因素确定和概率设计方法选取。在渣土边坡稳定可靠度问题中，衡量指标为稳定性系数，功能函数为[15]

G(ξ)=Fs(ξ)-1.0

(2)

式中：Fs(ξ)——渣土边坡稳定性系数；

ξ——独立正态分布随机量。

其中，由于Monte-Carlo法操作较为简便并且抽样结果较为合理，因此Monte-Carlo法被普遍应用于岩土工程可靠度设计[16]。本文选择Monte-Carlo模拟作为概率性设计方法，通过现场取样并进行相关室内试验，获得所需岩土体参数的数据，计算得到相应参数的概率模型。依据已知概率模型，采用编程模拟获得N组符合原始岩土体参数概率类型的随机样本点，进行概率计算。其中Monte-Carlo模拟次数N一般满足[16]：

N≥100/ζ

(3)

2.1 可控参数

可控参数指设计过程易于调整且对设计结果造成显著影响的结构参数[17]。在阻滑键加固边坡的工程实践中，并没有详细具体的设计规范，一般根据专家经验结合实际工程进行设计，设计参数主要包括阻滑键的几何参数和埋设参数等。根据相关工程实例[3-4]，阻滑键结构的预埋位置、尺寸、组数和间距参数易于调控，且对边坡的加固效果有显著影响，故设计可控参数选择阻滑键的预埋位置、组数、间距和尺寸。渣土边坡堆填时将平洞与竖井段充填为钢筋混凝土材料，即构成阻滑键单元的平肢段和竖肢段，预埋于潜在滑动面处；阻滑键整体顺滑面方向并按照各段的锚固段和承荷段长度相同的方式进行布置(图2)。

依据边坡坡表形状水平投影将渣土边坡近似三等分，分别记为渣土边坡前缘、中部和后缘，如图2所示。相应地，考虑阻滑键分别布置在渣土边坡前缘、中部和后缘的不同工况。将阻滑键的组数记为n。当n≥2时，每个阻滑键单元的预埋间距为d。为简化计算并方便衡量阻滑键尺寸参数，以阻滑键前竖肢段长度进行表述，将其记为L,单位为m。每个尺寸的阻滑键各段截面尺寸相同，均为矩形形状，为b×h(宽×高,单位为m)。

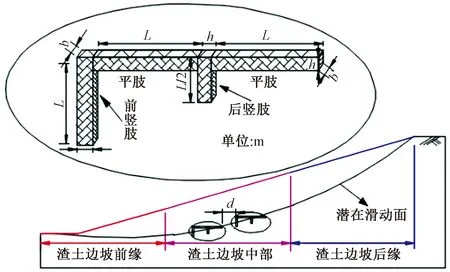
图2 阻滑键结构示意图(据郑轩等[4]，有修改)Fig.2 Schematic diagram of sliding resistant components [4]

2.2 不可控因素

不可控因素指难于控制的干扰因素，主要为渣土边坡岩土体物理力学参数，包含容重、内摩擦角、黏聚力、泊松比和含水率等。由于内摩擦角和黏聚力参数对边坡稳定性分析影响较大[17],本文采用岩土体的内摩擦角φ和黏聚力c作为多目标优化设计的不可控参数。

岩土体参数由于漫长地质力学作用显现出非均质性和各向异性等不确定性特征，在实际岩土工程分析常采用不同的参数概率分布类型刻画岩土体参数的不确定性分布。岩土体参数的概率分布类型对岩土体的可靠度分析有明显影响，有学者认为岩土体参数的概率分布类型接近正态、对数正态分布[18-19]。

实际研究区岩土体的内摩擦角φ和黏聚力c参数的概率分布类型，可根据现场岩土体取样进行室内实验，并结合统计分析获得。

2.3 基于可靠度理论的多目标优化设计方法

在考虑渣土边坡在不同设计参数下的预估破坏损失和岩土体参数的不确定性的基础上，结合可靠度理论，提出了阻滑键加固渣土边坡的多目标优化设计方法。主要流程包括以下四个步骤(图3)。

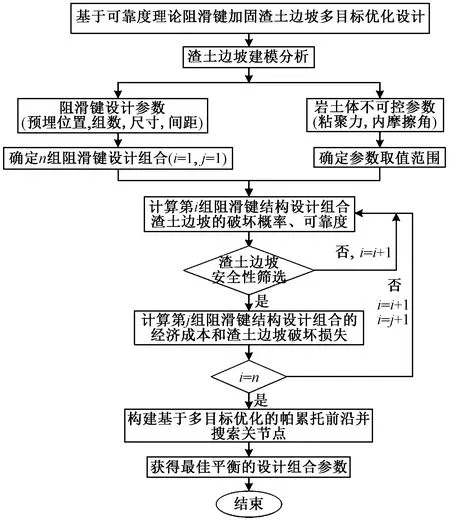
图3 阻滑键加固渣土边坡多目标优化设计流程图(据黄宏伟等[11]，有修改)Fig.3 Multi-objective optimization design flowchart of sliding resistant components for construction sediment slope reinforcement[11]

(1)针对具体的渣土边坡进行初步建模和参数分析。

(2)确定设计可控参数和不可控因素，明确参数范围：设计可控参数选择阻滑键预埋位置、组数、间距和尺寸；不可控参数为渣土边坡土体的内摩擦角φ和黏聚力с。

(3)确定目标函数并计算渣土边坡在不同设计方案下的破坏概率p和可靠度指标β。为保证渣土边坡的安全稳定，通过确定渣土边坡破坏概率(可靠度指标)的临界值p0(β0)，剔除稳定性较差的阻滑键设计组合。为减少过度安全造成的设计浪费，当破坏概率p0.6%或可靠度指标β2.5时，认为边坡处于稳定安全状态[20]，故p0取0.006，可靠度指标β0取2.5。功能函数公式(2)作为目标函数，利用Geo-Studio软件中的Slope/W模块，根据公式(3)采用Monte-Carlo计算16 103次，可计算得到渣土边坡在n个不同阻滑键组合情况下的破坏概率p和可靠度指标β，并根据临界值对阻滑键设计组合进行筛选。

(4)确定各个子目标并进行多目标优化。以阻滑键加固渣土边坡的破坏概率(可靠度指标)，支护成本及预估破坏损失作为多目标优化设计的目标量。通过计算不同阻滑键设计参数组合的造价，确定支护成本。通过卫星影像识别结合实地工程地质调查，走访估算承灾体总价值，计算不同设计方案下的渣土边坡预估破坏损失。基于多目标优化理论考虑设计成本、渣土边坡的预估破坏损失和安全稳定性三个子目标建立帕累托最优解集。

多目标优化问题中，由于多个目标相互冲突，通常不存在多个目标同时最优的理想设计，折中设计一般是优化的目标。通过帕累托最优解集确定帕累托前沿，帕累托前沿上的设计点在改进任何子目标时均会造成其他子目标的恶化[21]。关节点作为帕累托前沿上的特殊点，除此之外的任何设计点，若稍微优化一个子目标时均会造成其他子目标严重恶化，该关节点即为最佳阻滑键设计组合[22]。

3 工程实例分析

3.1 模型建立

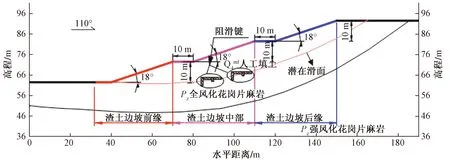
图4 深圳某渣土边坡的计算模型图Fig.4 Calculation model of a construction sediment slope in Shenzhen

在该渣土边坡取样进行了70组室内物理力学实验，并参考深圳地区岩土体参数试验报告，可确定该渣土边坡岩土体的物理力学参数，并采用AIC信息判别准则识别其抗剪强度参数c、φ的概率分布函数，置信度为95%，结果如表2和图5所示。

表2 渣土边坡计算模型基本参数取值表Table 2 The parameter values of landfill calculation model

图5 深圳某渣土边坡的岩土体概率分布Fig.5 Distribution of soil a construction sediment slope

基于Geo-Studio软件的Slope/W模块并结合Monte-Carlo方法，分别计算渣土边坡在每个潜在设计工况条件下的破坏概率和可靠度指标。本文依据实际工程经验确定阻滑键的设计参数[3-4]，采用Geo-Studio软件建立阻滑键加固渣土边坡模型进行计算。其中，阻滑键组数n=2时，阻滑键单元的间距d取5 m、10 m 和15 m。阻滑键尺寸参数L选取10组，L=1～10 m，前竖肢段每次设计增加1 m，后竖肢段的长度为前竖肢段的1/2。综上，阻滑键设计方案共2×3×3×10=180种工况(表1)。

表1 阻滑键设计参数范围Table 1 Design parameters for sliding resistant components

3.2 多目标优化设计

根据本文提出的多目标优化设计方法流程，可计算得到渣土边坡在不同潜在设计工况条件下的破坏概率和可靠度指标(图6)，并对潜在设计方案进行了初步筛选。破坏概率值位于直线p0=0.006以下或可靠度指标在直线β0=2.5以上的阻滑键设计组合均满足渣土边坡稳定和安全最低要求的设计组合。为获得渣土边坡多目标优化设计的最优方案，需要综合考虑防护结构的造价和渣土边坡预估失稳后的期望破坏损失。

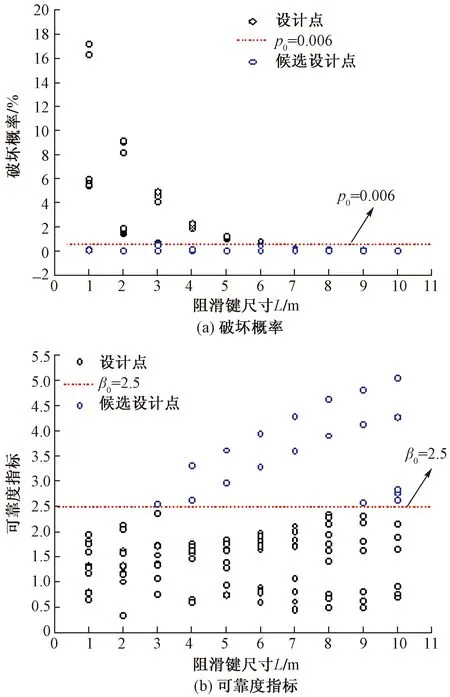
图6 多目标设计计算的渣土边坡破坏概率和可靠度指标Fig.6 Failure probability and reliability of construction sediment slope with multi-objective design calculation

结合工程实践，阻滑键造价主要根据单位体积的混凝土造价c1和单位质量的钢筋造价c2进行计算。依据相关市场报价，C30混凝土造价的参考价格约300元/m3，阻滑键钢筋的参考价格为2 500元/t[23]，计算公式如下：

c=c1+c2

(4)

阻滑键加固渣土边坡后，渣土边坡将会沿着新的滑动面发生破坏。不同的阻滑键设计方案加固渣土边坡后，渣土边坡破坏规模也不同(图7)。渣土边坡的预估破坏损失主要包括预估不同破坏强度下，渣土边坡失稳后的滑动土体覆盖周边房屋、公路等造成的期望经济损失。根据卫星影像和现场勘察确定该渣土受纳场边坡实例危险范围内的建筑物和道路等承灾体的数量和重要程度，并收集建筑价格、道路规格、居民年龄和教育程度等，估算渣土边坡不同危害范围内道路、房屋和人等承灾体的价值。渣土边坡失稳可能造成的预估破坏损失估算公式如下[24]：

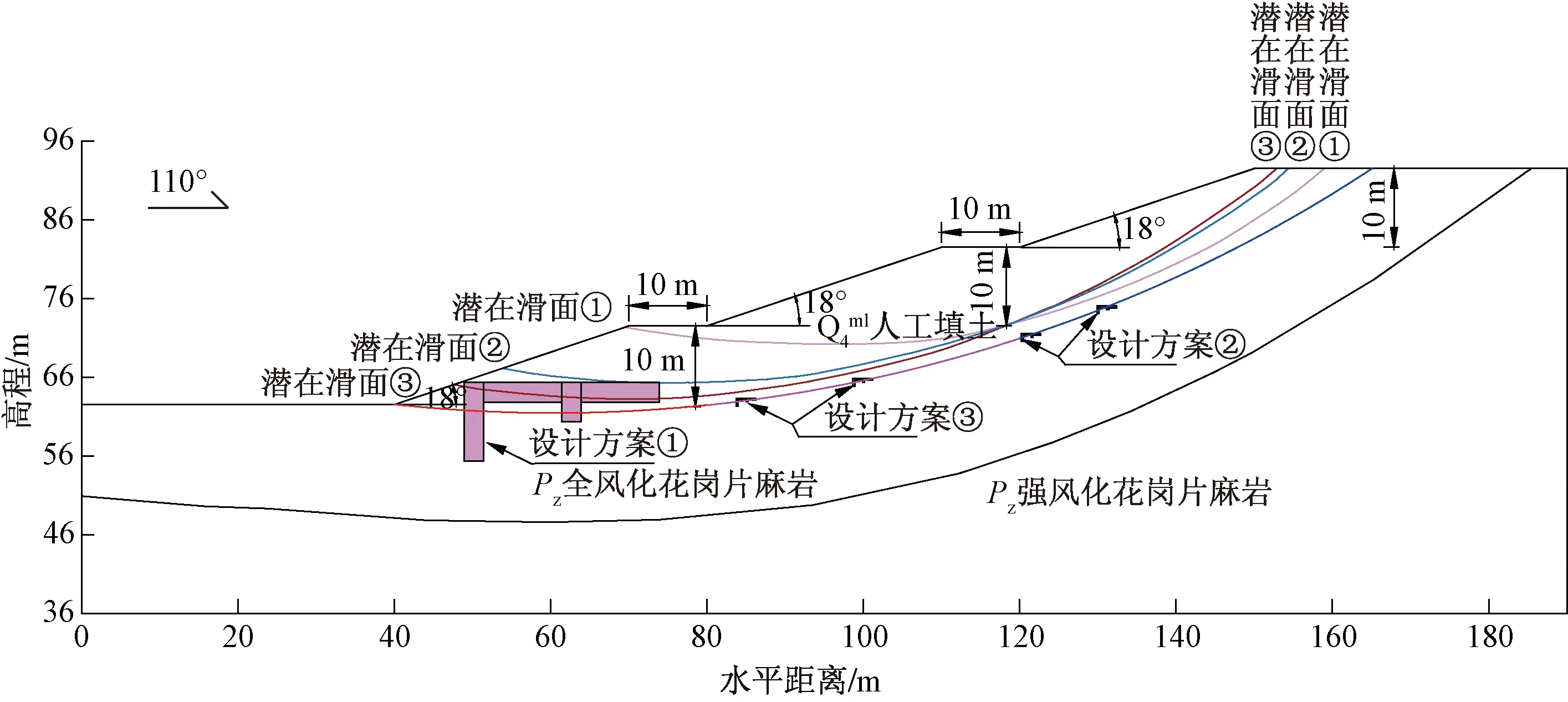
图7 不同设计方案下边坡的潜在破坏规模Fig.7 Potential failure scale of slope with different design schemes

S=Pj×∑W×Vj

(5)

式中：S——渣土边坡失稳的预估破坏损失/千元；

Pj——第j组阻滑键设计参数时渣土边坡的破坏概率/%；

W——该渣土边坡承灾体的总价值/千元；

Vj——第j组阻滑键设计参数时渣土边坡破坏规模比率，为阻滑键加固后渣土坡体的破坏规模比上渣土边坡总规模，无量纲。

考虑岩土体参数的不确定性进行边坡工程设计时，计算得到的破坏概率P是岩土体参数在随机情况下边坡小于1的稳定性系数所占的比例，反映了边坡发生失稳的可能性。而可靠度指标β反映了稳定性系数的平均情况和离散程度。设计过程中认为计算得到的破坏概率足够小或可靠度指标足够大时，边坡工程的设计是可靠安全的。故本文将破坏概率或可靠度指标作为衡量渣土边坡安全稳定指标，并结合阻滑键结构的造价和渣土边坡的预估破坏损失进行优化分析，确定帕累托最优解集，建立帕累托前沿。帕累托前沿上的设计组合既能满足设计的安全性，又具有较好的经济效益和较小的潜在危害、损失[21]。关节点是帕累托前沿中同时具有经济性、安全性和稳定性并达到多目标平衡的最佳折中设计组合点，主要由下式计算得到[22]：

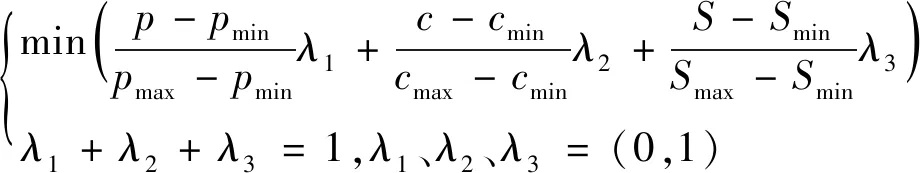
(6)

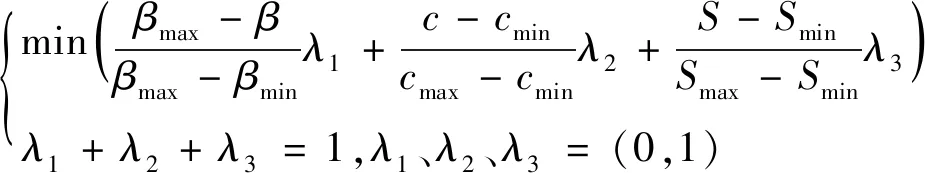
(7)

式中：p——渣土边坡的破坏概率值；

pmax——破坏概率最大值；

pmin——破坏概率最小值；

β——渣土边坡的可靠度指标值；

βmax——可靠度指标最大值；

βmin——可靠度指标最小值；

c——造价；

cmax——造价中的最大值；

cmin——造价中的最小值；

Smax——预估破坏损失的最大值；

Smin——预估破坏损失的最小值；

λ1，λ2，λ3——破坏概率(可靠度指标)、造价和预估破坏损失的权重系数。各目标的权重系数值受具体工程重要性和设计人员的偏好等影响。在实际操作中，可根据实际工程中的不同要求选取合适的权重值。为简化计算，此次计算中权重系数均取相同值，即λ1=1/3，λ2=1/3，λ3=1/3。

由图8可知，渣土边坡的破坏概率随着阻滑键造价的增加明显降低，而可靠度指标则明显提高。帕累托前沿上的设计组合均是优化设计可行方案。在帕累托前沿上，设计组合1造价最低，预估破坏损失最大且阻滑键加固渣土边坡效果最差；设计组合3造价最高，预估破坏损失最小，阻滑键加固渣土边坡效果最佳。设计组合1和组合3均属于极端设计，未能达到渣土边坡安全稳定和经济效益的平衡。而设计组合2作为帕累托前沿的关节点，造价适中，阻滑键结构加固效果较好，预估破坏损失较小，渣土边坡较为安全，渣土边坡防控工程的经济性和安全稳定性达到平衡，是最佳设计组合。

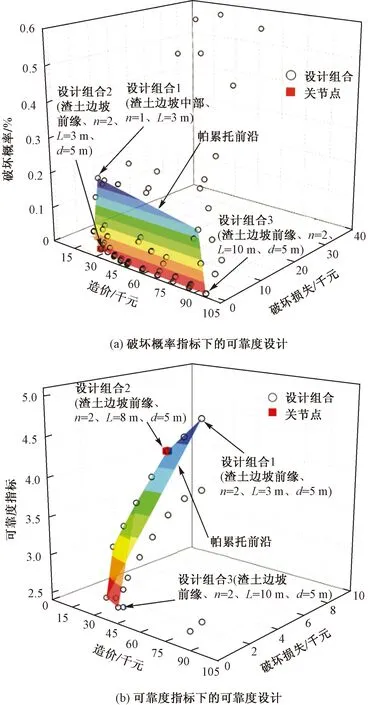
图8 可靠度设计多目标优化Fig.8 Multi-objective optimization for reliability design

在图8(a)中将破坏概率作为衡量渣土边坡安全稳定指标时，设计组合2是两组尺寸长3 m、间距为 5 m 预埋在渣土边坡前缘的阻滑键；在图8(b)中将可靠度指标作为衡量渣土边坡安全稳定指标时，设计组合2是两组尺寸长8 m、间距为5 m预埋在渣土边坡前缘的阻滑键。其中，破坏概率作为衡量指标时，设计组合2的造价和预估破坏损失较可靠度指标作为衡量指标时的最佳设计组合均低，更为经济安全。考虑到防治结构设计的工程实际情况，需保证安全性与经济性之间的平衡，即在保证设计安全的前提下使投入成本最低，因此本次实例选择破坏概率指标下的设计组合2作为多目标优化的最优设计。在实际工程应用时，可根据工程特殊要求采取最优的综合设计方案。

3.3 阻滑键布设参数分析

由上述实例分析可知，该渣土边坡阻滑键的最优设计方案均是在渣土边坡前缘预埋两组间距为5 m的阻滑键。为进一步研究布设参数对阻滑键优化设计的影响，进行不同布设参数预埋阻滑键加固渣土边坡的效果分析。

图9中分别给出了阻滑键布设参数与渣土边坡破坏概率和可靠度指标的关系曲线。考虑岩土体参数不确定性时，阻滑键预埋位置基本不影响渣土边坡的破坏概率；同一位置预埋不同布设参数的阻滑键时，渣土边坡的破坏概率对阻滑键结构的间距、组数等布设参数变化响应较为显著，而布设2组间距10 m阻滑键与1组阻滑键破坏概率基本相同，布设2组间距5 m的不同尺寸的阻滑键时破坏概率基本相同。然而，不同位置预埋不同尺寸、组数、间距的阻滑键，渣土边坡的可靠度指标变动较大，即稳定性系数离散程度变化较大，布设2组间距10 m阻滑键与1组阻滑键时渣土边坡的可靠度指标基本相同。在渣土边坡前缘和中部埋设阻滑键结构时，可靠度指标对结构间距、组数等布设参数变化响应较为显著；而在渣土边坡后缘时，随结构间距、组数等布设参数改变，可靠度指标变化无规律，较为离散。

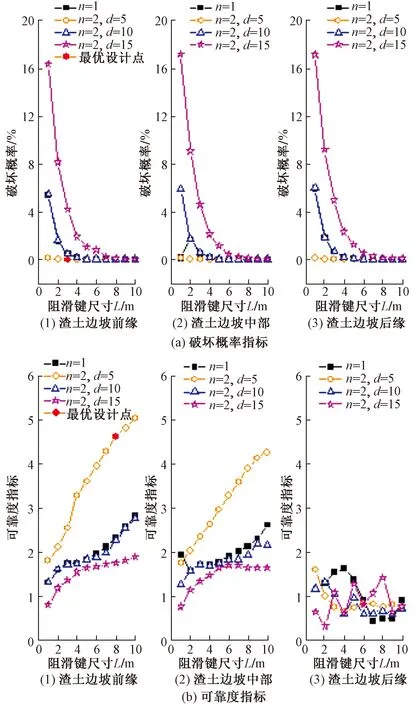
图9 不同阻滑键布设条件下的渣土边坡破坏概率和可靠度指标Fig.9 Failure probability and reliability index of the slope under different design parameter of the sliding resistant components

经分析，连续阻滑键竖肢段作用机理与抗滑桩近似。在渣土边坡前缘和中部加固渣土边坡时，阻滑键的锚固深度较为适中，结构和土体的相对位移一般较大，加固坡体范围较广，结构的阻滑作用得以充分调动、发挥，加固效果较为显著，布设组数增加时阻滑键结构置换潜在滑动面的范围扩大，潜在滑动面的强度提高，随着布设间距的扩大，置换区域贯通性降低，加固效果显著降低。而埋设在后缘的阻滑键结构加固坡体范围局限在坡体上部，可能会增加渣土边坡坡体荷载导致阻滑键结构下部的坡体失稳，故破坏概率与其他位置埋设基本相同，而稳定性系数的离散程度变化较大，即可靠度指标变动较大。

总体上，在渣土边坡前缘埋设2组间距5 m的阻滑键对渣土边坡的加固效果更显著，阻滑键优化设计的预埋位置也多集中于渣土边坡前缘。

4 结论

(1)考虑岩土体参数的不确定性、阻滑键结构和渣土边坡预估破坏损失，基于可靠度理论，本文提出了阻滑键加固渣土边坡的多目标优化设计方法。最低造价设计容易降低加固效果，最高造价设计过度注重安全性和稳定性会增大经济成本，多目标优化设计可有效达到阻滑键设计成本、渣土边坡的稳定安全性和预估破坏损失之间的最佳平衡。

(2)在工程实例中，确定帕累托前沿并计算关节点获得最优设计参数。当选择破坏概率作为渣土边坡安全稳定指标时，关节点为在渣土边坡前缘预埋两组尺寸长3 m、间距为5 m阻滑键的设计参数组合，是该多目标优化设计的最优设计点。实际工程设计中应根据工程需要选择适合的安全性评价指标或同时采用破坏概率和可靠度指标进行多目标优化设计。

(3)在渣土边坡后缘预埋相同布设参数阻滑键时，可靠度指标变化较大，稳定性系数平均值接近而离散程度较大；在本文案例的渣土边坡前缘和中部埋设2组间距5 m的阻滑键结构加固渣土边坡效果显著。本文的优化设计方法可进一步推广应用到不同边坡和不同防护结构的优化设计。