改进A*算法的智能车路径规划研究
2020-11-03付克昌向泽波刘甲甲
杨 瑶,付克昌,蒋 涛 , 向泽波,刘甲甲
(1.成都信息工程大学 控制工程学院,成都 610225; 2.中国科学技术大学 软件学院,合肥 230000)
0 引言
随着智能驾驶技术的快速发展,将智能车运用在日常生活中的可能性也越来越大。而智能驾驶技术是实现智能汽车与智能交通的关键技术,也是未来汽车发展的趋势[1]。目前,学者们对路径规划方法进行了大量研究,主要包括:基于采样的快速搜索随机树[2]等方法;基于节点A*算法[3]等;基于模型的人工势场法[4]等;基于生物启发式的蚁群算法等[5]。其中,A*算法是能够有效求解出最优路径的完备规划算法[6],也是在机器人上使用最广泛的规划算法之一。但传统A*算法仍存在一些问题。如:所规划的路径不平滑[7],路径紧贴障碍物[8]和不满足车辆运动学等问题。针对上述问题,本文通过对车辆进行建模分析,得到车辆最大转向角约束和最大曲率约束,并与A*算法的启发函数相结合使得扩展节点的代价值更为合理。同时,提出车身轮廓代价消除传统A*算法在扩展过程中遍历不合理的节点。并提出障碍物距离代价,解决了所规划的路径贴合障碍物的问题。然后,提取出改进A*算法的转折点,并将车辆最大曲率约束与转折点相结合得到适合智能车行驶的转折点,再使用贝塞尔曲线拟合转折点得到最优路径。通过上述改进使得A*算法所规划出的路径更加符合车辆的运动学特性并便于实现智能车的路径跟踪。
1 车辆的运动学模型
车辆是一个非完整性约束的系统[9],分析较为困难,因此本文只考虑车辆的简化运动模型(如图2所示)。本文的实验平台为野马E70电动汽车(如图1所示)。在图2中的惯性坐标系XOY下,(x,y) 为车体在此坐标系下的坐标位置,φ为车体的横摆角(航向角) (φ<φmax),l=1.56米为智能车的轴距,R为智能车的转弯半径,θ为车辆纵轴与x轴之间的夹角,D=1.835 m为智能车的车宽。本文中只考虑车辆在二维平面上运动,不考虑俯仰和侧倾带来的影响[9]。在车辆运动瞬间,车辆的速度与车体保持平衡,即满足:
dx*cos(θ)-dy*sin(θ)=0
(1)
(2)

图1 基于野马E70电动汽车改造的智能车驾驶平台

图2 本文车辆简化运动学模型
Kmax=16 m-1车辆最大转弯曲率,Rmin=8 m 车辆最小转弯半径,φmax=40°车辆最大转向角。
2 A*算法
A*算法是一种在静态路网中求解最优路径的最有效的搜索算法,也是解决其他搜索问题的有效算法。A*算法的评价函数的一般形式为:
f(n)=g(n)+h(n)
(3)
其中:f(n)是从初始点到节点n的代价和节点n到目标点的估计代价的总和,g(n)是在状态空间中从初始点到节点n的实际代价,h(n)是从节点n到目标点的估计代价。
A*算法的基本步骤:
1)在栅格地图上获得起始点和目标点并初始化开启列表和关闭列表。
2)将起始点添加入开启列表中,并将起始点作为父节点添加到关闭列表中。
3)将父节点四周与障碍物无碰撞的扩展节点添加到开启列表中并计算其扩展节点的代价值,再判断扩展节点是否为目标点。如果是,则从关闭列表中得到路径,结束规划。否则执行步骤4)。
4)从开启列表中,取得最小代价值的节点作为父节点并将此节点添加到关闭列表中。 再执行步骤3)。
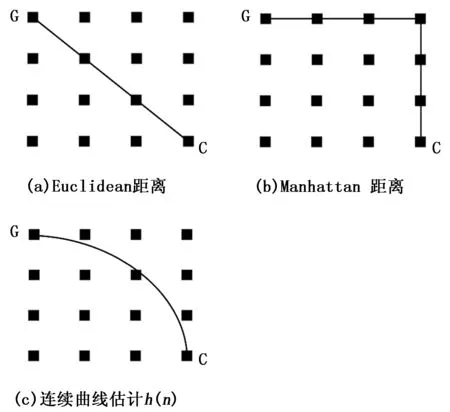
传统的A*算法的h(n)多数采用Manhattan距离和Euclidean 距离进行估计,并未考虑车辆的运动学特性和车辆的体积。因此传统A*所规划出来的路径往往不具有连续的曲率,且因转折次数过多等导致不满足车辆运动学特性。
3 改进A*算法
为了解决传统A*算法所规划的路径不适用于智能车的问题,本文对传统A*算法进行改进。首先,将传统A*算法的启发函数h(n),用连续曲线替代。其次,提出车身轮廓代价和障碍物距离代价解决所生成的路径贴合路沿的问题。同时,对车辆进行运动学建模得到车辆约束条件,将约束条件带入A*算法所规划路径的转折点中。最后,使用贝塞尔曲线对转折点进行拟合。
改进 A*算法中的评价函数定义为:
f(n)=g(n)+h(n)×(1+o(n))+s(n)
(4)

(5)
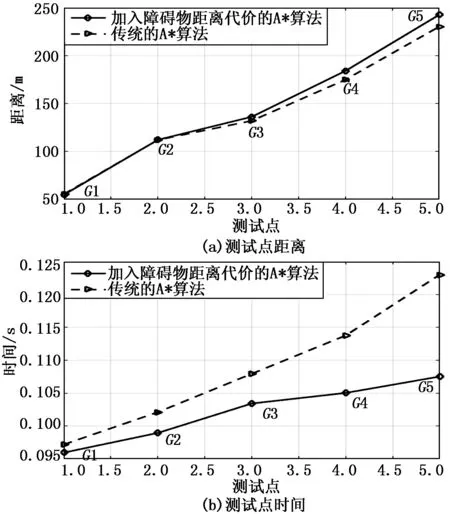
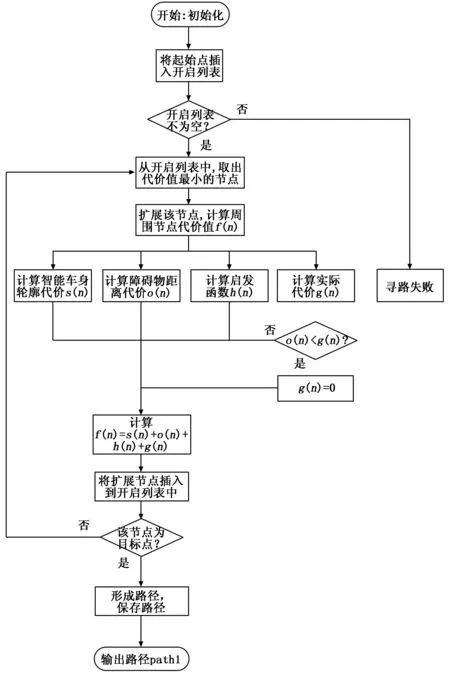
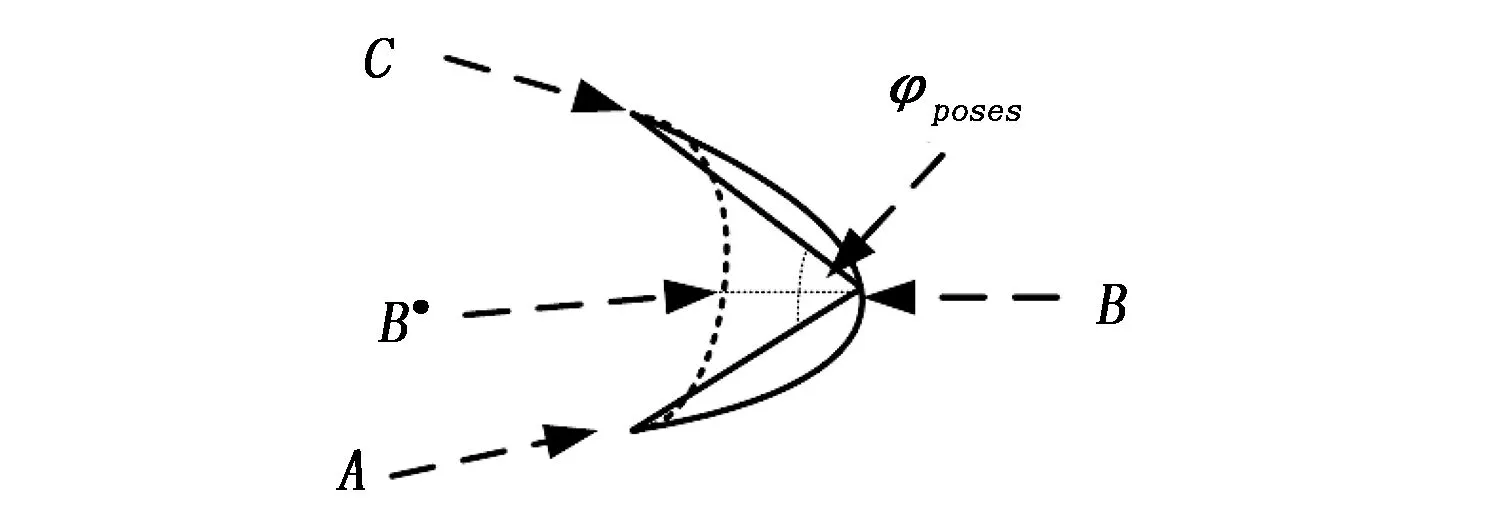
其中:o(n)是障碍物距离代价,s(n)是智能车轮廓代价。公式(5)中,当g(n) 由于传统A*算法的h(n)一般使用Euclidean距离和Manhattan 距离对扩展节点的代价值进行估计,所以往往会造成扩展节点被过小估计或者过大估计。比如:Euclidean距离(如图3(a)所示)通过计算扩展节点到目标点的直线距离会造成对h(n)估计过小的问题。而Manhattan 距离(如图3(b)所示)是由扩展节点和目标点的x和y绝对值之差相加所得到,会造成对h(n)估计过高的问题。因此,本文使用圆弧曲线对h(n)进行估计较为合理(如图3(c)所示)。此外,由于智能车行驶路线为连续可导的曲线,而Euclidean距离和Manhattan 距离都是不连续且估计的代价值相较图3(c)所估计的代价值误差较大。 图3 启发函数h(n)代价值示意图 (6) (7) 图4 曲线估计示意图 因为智能车具有一定的体积且存在着最小转弯半径的问题,所以不能当成一个质点处理。同时,传统A*算法在扩展过程中会扩展到贴合障碍物的节点(如图9中的扩展节点),这对于智能车来说是没有必要的。此外,传统A*算法规划中未能考虑路径与障碍物的距离。这些问题导致所规划的路径不能很好被智能车所执行。对于这个问题,马飞[8]等人提出碰撞威胁代价来解决A*算法所生成的路径贴合障碍物的问题,但是通过在每个扩展节点上加入铲运机9个轮廓特征点来计算碰撞代价,会导致程序计算量增加。因此,本文通过判断扩展节点p(n)=(x1,y1)四周距离的障碍物检测点(如图8所示)是否有为障碍物来对c(n)进行赋值。如果有,则将该节点赋为无穷大,否则赋为零。 图5 障碍物监测点示意图 为了测试本文的车身轮廓代价,本文参照文献[8]的方法在智能车的简化模型上加入碰撞检测点,如图9所示。同时,采用文献[8]的方法对扩展节点进行打分判断,并在图7的测试点上进行测试分析(L=5.555米表示车长,D表示车宽)。 图6 智能车简化模型的碰撞检测点 图7 测试点坐标位置显示 图7中的坐标点为所测试的起始点和目标点,其中S表示起始点,分别选取G1,G2,G3,G4,G5作为目标点。 图8 两种不同的方法在测试点的测试对比 在图8(a)中,x轴表示在图7所示的测试点,y轴表示规划出路径的距离;在图8(b)中,x轴表示在图7所示的测试点,y轴表示规划出路径的时间。同时,通过图8的(a)和(b)所示,采用车身轮廓代价和典型的惩罚代价所规划的路径和时间对比可知:两种方法所规划的距离相差不大,但是所用的时间存在的一定差距。相比使用典型的惩罚代价,通过使用本文的车身轮廓代价能够减少算法运行的时间。此外,虽然加入车身轮廓代价的A*算法所规划的距离有一定的增加,但是所用时间比传统A*算法所用的时间少,这说明本文的车身轮廓代价是具有一定的优势。 本文优化步骤如下: 1)判断扩展节点四周的障碍物检测点是否为障碍物。 2)如果是,则在扩展节点上增加障碍物标志位。否则,进行执行3)。 3)判断扩展节点是否为目标点。如果否,则执行步骤1);如果是则形成路径。 图9 道路示意图 为了进一步使规划的路径更为合理和可靠,本文采用Voronoi地图对规划所需要的栅格地图进行处理[10]。其中,Voronoi地图是距离地图和广义泰森多边形相结合组成。首先,通过Voronoi地图获得扩展节点到达障碍物的最近距离dmin。然后,将该距离作为约束条件带入到代价函数中,如式8所示: (8) 在式(8)中,δ表示障碍物安全距离代价的常数。dmin取倒数是因为A*算法是选择代价值最小的节点作为扩展节点,距离障碍物越远的节点对于智能车来说应该是越安全,因此应该优先考虑该节点。 图10为加入障碍物距离的A*算法和传统A*算法在图7上的测试结果。其中,在图10(a)中,x轴表示在图7所示的测试点,y轴表示规划出路径的距离;在图10(b)中,x轴表示图7中的测试点,y轴表示规划出路径的时间。通过图10(a)可以看出加入障碍物距离后的A*算法和传统A*算法在测试点所规划的路径距离大致相等。在G1,G2所测试的时间差距不大,但是在后面的测试结果中传统A*算法所用的时间与改进后的A*算法所用时间差距越来越大,如图10(b)所示。 图10 两种不同的方法在测试点的测试对比 改进A*算法流程如图11所示。 图11 改进A*算法流程图 由于车辆在转向中存在最小转弯半径,不能像麦克纳姆轮一样全向移动。而传统的A*算法所规划出的路径转折数目太多且不够平滑,使得车辆在贴合路径时,摇摆不定。所以必须对规划出来的路径进行一步优化,使其路径更加适用于车辆的运动特性。优化步骤如下: 1)首先获得改进A*算法的路径path1,并删出冗余点[11],得到转折点。 2)依次从path1中取pose[i-2],pose[i-1], pose[i]进行拟合y(x)1=a*x2+b*x+c。同时,判断提取出来的转折点中,是否包含终点。如果含有终点,保存转折点到path2,结束对转折点优化的过程。否则,执行下一步。 4)重复步骤2)。 (9) K (10) indexnew= (11) indexnew是移动后节点的索引,index是此刻节点的索引,nx表示地图的宽度。(如图12所示)。 图12 改进A*算法所规划路径后优化流程图 图13 改进A*算法转折点移动示意图之一 为了使所规划路径更为平滑,有将转折路径用圆弧所替代已形成光滑路径[12],也有用贝塞尔曲线或者样条曲线等方法对路径点优化的。本文采用贝塞尔曲线[13]对改进A*算法的路径进行平滑处理。其中,贝塞尔曲线是法国工程师皮埃尔.贝塞尔在1962年提出,其形状可由曲线的控制点确定。因此,将改进改进A*算法所规划的路径点作为贝塞尔曲线的输入,消除路径不平滑的情况。 使用不同拟合方法示意图如图14所示,其中A点,B点和C点表示改进A*算法的路径点。从图14可以看出,使用二次样条插值所生成的路径的曲率较大,二次B样条曲线拟合的起始点是A点和B点连线的中点,目标点是B点和C点连线的中点,导致所生成的路径在起始点和目标点处不连续,而使用二次贝塞尔曲线拟合能够较好解决上述二次样条插值和二次B样条曲线拟合所带来的问题。 (12) B(t)=(1-t)2*P0+2*t(1-t)*P1+t2*P2t∈[0,1] (13) 公式(12)为贝塞尔曲线的一般方程,公式(13)是本文所使用的二阶贝塞尔曲线,P0,P1,P2为二阶贝塞尔曲线的控制点。 为了验证改进后的A*算法的有效性,本文分别将Dijkstra算法、A*算法(使用Manhattan距离)、A*算法(使用Euclidean距离)和改进A*算法应用于成都信息工程大学校园的栅格地图(4 846 ×2 816)上,如图15所示,栅格大小为0.298 m/pixel,选择不同的地点进行实现。同时,本实验基于ROS(开源机器人操作系统)平台,并使用Rviz进行可视化。计算机配置为:Ubuntu16.04 LTS,处理器Intel i5-6500,主频为3.2 Ghz,运行内存为8 G。 本次实验通过在地图上选择起始点和终点,上述4种算法进行路径规划。通过比较规划路径的长度、与障碍物的距离、路径最大转角和遍历的节点数等方式来进行判断路径的优劣。对区域一、区域二和区域三进行路径规划,规划结果见图16、图17和图18。表1、表2和表3分别给出了不同区域规划的指标对比。 图15 学校的校园地图 图16 在区域一测试的结果 图17 在区域二测试的结果 图18 在区域三测试的结果 从图16、图17和图18中可以看出,改进的A*算法所规划出来的路径较为平滑,具有连续的曲率并能够较好地满足车辆运动学模型。同时,Dijkstra算法、A*算法(使用Manhattan距离)、A*算法(使用Euclidean距离) 在测试区域测试中都存在起始时刻路径转折角度过大,路径贴合路沿,路径不平滑和转折次数较多等问题。在加入车身轮廓代价、障碍物距离代价和对路径优化过后能够较好地解决这些问题(如图16、17和18的(d)图所示)。这都说明改进后的A*算法能够更好地解决传统A*算法路径规划所存在的问题。 表1 区域一测试对比 表2 区域二测试对比 由表1、表2和表3中能够看出改进后的A*算法规划时间小于Dijkstra算法、A*算法(使用Manhattan距离)、A*算法(使用Euclidean距离)的规划时间。同时,所遍历的节点数最少,并且与路沿的最近距离都大于车身宽度 表3 区域三测试对比 的一半。此外,改进A*算法所生成路径的最大转角都是小于车辆最大转向角。因此,通过该方法所生成的路径是能够被智能车所执行的。 本文针对传统A*算法所规划的路径转折角度较大,路径不平滑,所规划的路径贴合障碍物和未考虑车辆自身约束条件等问题进行改进,得到如下结论: 1)通过建立车辆运动学模型得到约束条件将其带入启发函数中使得节点代价值更为合理。 2)利用车身轮廓代价去掉A*算法所存在不合理的扩展节点,进而减少A*算法所遍历的节点数目。 3)通过加入障碍物距离代价解决路径靠近障碍物的问题,使得所规划的路径更为合理,更为安全。 4)使用贝塞尔曲线对路径转折点进行拟合使所规划的路径更平滑,更适用于智能车的运动特性。 5)由于本文算法是主要针对于在实验阶段中的AGV或者智能车,并且所实验的载体是在中低速的环境中运行。其次,将该算法进行改进并用于高速行驶的移动载体是后续研究的重点。3.1 对函数h(n) 进行改进



3.2 车身轮廓代价s(n)




3.3 障碍物距离代价o(n)


3.4 路径优化




3.5 路径平滑
4 算法验证







5 结束语
