基于学生成绩回归预测的多模型适用性对比研究*

喻铁朔 李霞 甘琤

摘   要：学生成绩预测是教育数据挖掘在教学实践中的一大重点，相比分类成绩预测的单一结果，回归成绩预测更能深化预测在教学实践中的意义。文章基于H2O框架下广义线性模型（GLM）、深度学习（DL）、梯度提升树（GBT）以及支持向量机（SVM）四种主流模型进行回归预测比较研究。从模型预测精度、预测结果对比、预测误差分析三个角度分析4种模型，在不同课程、不同课程属性下的适用性。结果表明，DL模型适用于专业课程，SVM模型适用于公共课程，回归模型的成绩预测受到离群数据影响较大，各模型对离群数据解释能力较弱。

关键词：学生成绩预测;回归模型;多模型对比;误差分析

中图分类号：TP301.6 文献标志码：A 文章编号：1673-8454（2020）17-0023-06

一、引言

在高校的教学过程中，学生课程成绩是衡量学生知识掌握程度和教师教学质量的主要依据。当下，高校信息化建设逐步转化为智慧校园建设，在此过程中积累了海量的数据，应用教育数据挖掘方法与数据相结合能够实现学生未来的成绩预测。周庆等[1]针对EDM（教育数据挖掘）的研究特点、不足及发展趋势进行了归纳，阐述了各类预测算法的应用场景及优缺点。利用数据挖掘技术进行回归成绩预测能够给学生提供课程学习指引、帮助学生规避学业风险，也能够为教师和管理者的教学重点和管理方案提供决策支持。

目前国内外有许多预测方面的研究，在学业预测方面，Goker H等[2]通过学生的基本信息与课程信息，应用贝叶斯分类方法改进早期预警系统预测学生未来学业成就，并发现影响学生学业的主要因素。Francis等[3]将学生特征分为人口特征、学术特征、行为特征和额外特征四个方面进行不同的组合，运用聚类算法和分类预测相结合的混合算法构建学习成绩预测模型。刘博鹏等[4]通过动态特征提取和偏互信息（PMI）对学生特征进行选取，并通过交叉验证方法对支持向量机（SVM）算法进行动态参数调整后实现成绩预测。孙力等[5]运用C5.0决策树方法，通过分析网络学历教育本科生的相关信息，实现英语统考的成绩预测，并提出相应策略来提高英语学习水平和考试通过率。

数据挖掘预测方法在其它领域中应用也十分广泛，张慧玲等[6]针对风电场的数据特征变化采用三种主流的预测算法进行适应性对比研究，通过预测精度、计算效率及模型适应性比较模型优劣势。李静等[7]采用BP神经网络、支持向量机、LSTM模型針对基因工程领域未来研究热点趋势进行预测，并对比分析三种模型的优劣。

现阶段的EDM研究预测主要以分类问题为主，预测模型大多单一且相应的分类预测结果不能对预测结果进行有效的分析。在课程成绩预测过程中，预测课程不同，相应模型拟合效果也不同。本文针对上述问题，拟进行回归类型的成绩预测，采用GLM（线性回归模型）、Deep Learning（深度学习）、GBT（梯度提升树）、SVM（支持向量机）四种主流的预测算法分析其在不同课程属性下的特性。从预测精度、误差分析、预测分布3个方面对四种算法进行比较，针对高校学生课程成绩预测，选取不同训练样本，提供合适的预测算法参考依据。

二、预测对比流程

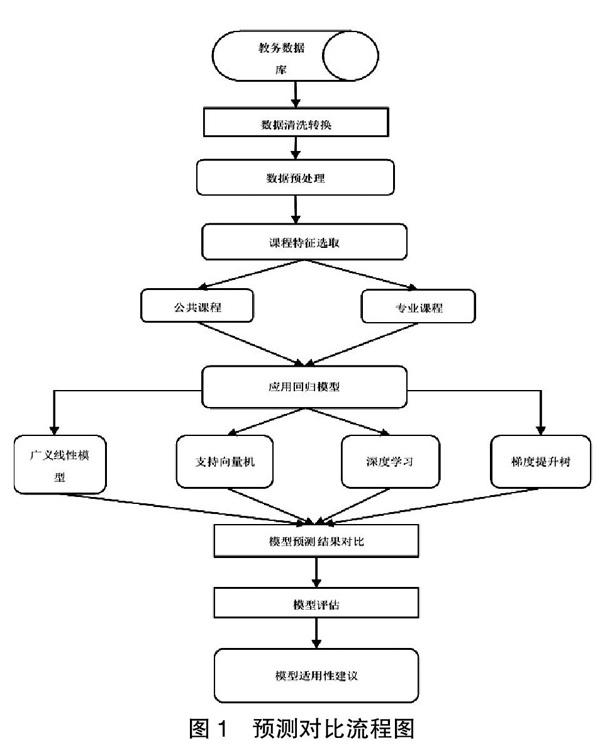
本文基于四种主流的学生成绩回归预测方法步骤如下：①从高校教务数据库中获取学生信息;②对抽取的数据完成数据清洗转换;③对清洗后的数据进行数据预处理;④进行课程特征选择，选取不同类型课程进行预测;⑤模型应用评估，选取合适算法进行对比分析，提供适合不同课程的算法。具体算法流程如图1所示。

1.GLM模型

文章使用H2O（3.8.26版本）框架执行GLM模型、DL模型、GBT模型，H2O是开源的、分布式的、基于内存的、可扩展的机器学习和预测分析框架。[8]广义线性模型（GLM）是传统线性模型的扩展。该算法通过使对数似然值最大来拟合广义线性模型，弹性净罚可用于参数正则化，模型拟合计算是并行的，速度极快，并且对有限数量的非零系数预测因子的模型具有极好的可伸缩性。广义线性模型有三个组成部分——随机部分、系统部分和联结函数。

随机部分：属于指数分布族的相互独立的随机变量yi，密度函数为：

f（yi|θi，φ）=exp（c（yi，φ））（1）

其中θi和φ为参数，b和c为函数。yi的期望是μi方差为均值的函数，则E（yi）=μi=b'（θi），var（yi）=b'（θi）。其中b'（θ）和b''（θ）分别表示函数b的一阶和二阶导数。

系统部分：假设x1，x2，…，xp为对应于y1，y2，…，yn的p维自变的值，存在某线性预估量η，参数β1，β2，…，βp的线性函数有：

η=xTβ=∑p   i=1xi βi（2）

联结函数：联结函数是指观测值xi与指数散布族的期望μi之间的函数关系。随机部分和系统部分通过ηi=g（μi）连接在一起，g（x）称为联结函数。容易得到：

g（μij）=x' ij β，i=1，2，…，p.（3）

其中，β为未知实参数，xTi=（xi1，…，xin）表示第i个观测向量。

2.Deep Learning模型

在H2O框架中深度学习是基于人工神经网络（ANN），是最常见的深度神经网络类型，也是H2O-3中唯一支持的类型。[9]该网络采用反向传播的随机梯度下降训练，可以包含大量的隐藏层，由具有tanh、整流器和maxout激活功能的神经元组成。也可以实现如自适应学习率、率退火、动量训练、L1或L2正则化和网格搜索，能够使预测精度更加准确。在模型训练过程中，每个计算节点使用多线程（或异步）在其本地数据上训练全局模型参数的副本，并通过网络模型定期平均地向全局模型传输参数。

应用深度学习算法需要设置激活函数、分布函数和损失函数两个重要参数，在H2O框架中深度学习主要使用Tanh（双曲正切函数）、Recrified Linear（线性整流器）、Maxout（最大输出）三种主要激活函数，文章选用Recrified Linear。

f（α）=max（0，α）（4）

在H2O中常用的分布函数有AUTO（自适应分布）、Multinomial（多项式分布）、Gaussian（高斯分布）、Laplace（拉普拉斯分布）、Huber（霍尔分布）、Poisson（泊松分布）等，每一个分布都有对应的损失函数。Multinomial分布对应交叉熵损失函数（cross-entropy loss），Gaussian分布对应于均方差损失函数（Mean Squared Error Loss），Laplace分布对应于绝对值损失函数（Absolute Loss），Huber分布对应霍尔损失函数（Huber Loss），对于Poisson分布等一些函数损失函数不能改变，所以损失函数设置为AUTO。具体损失函数如下：

L（w，B|j）=‖tj-oj‖22（5）

3.GBT模型

梯度增强树模型又可以称为GBM（梯度增强机）是回归或分类树模型的集合。这两种方法都是通过逐步改进的估计获得预测结果的前向学习集成方法。该方法的指导思想是通过不断改进的近似来获得良好的预测结果。H2O 中构建的GBT以完全分布式的方式，在数据集的所有特征上依次构建回归树——其中每棵树都是并行构建的。GMT计算步骤如下：

输入训练数据（xi，yi），构建提升树模型fM（x），初始化f0（x）=0。对于第m个基学习器，首先计算梯度：

gm（xi）=f（x）=fm-1（x）（6）

根据梯度学习第m个学习器：

Θ'm=arg min∑N  i=1[-gm（xi）-βmΘ（xi）]2（7）

θ，β

通过line search求取最佳步长：

βm=arg min∑N  i=1L[yi，fm-1（xi）+βmΘ'm（xi）]（8）

β

令fm=βmΘ'm，更新模型，最后输出f（xi）：

f（xi）=fm-1+fm（9）

4.SVM模型

SVM（支持向量机）的算法是一个易于使用、快速高效的SVM模式识别和回归的软件包。SVM在实际应用中可以分为SVC（支持向量分类）和SVR[10]（支持向量回归）两种方法。LIBSVM对于回归任务支持epsilon-SVR和nu-SVR实现。支持向量回归模型的目标是让训练集中的每个点（xi，yi）拟合到一个线性模型，形式如下：

yi=？棕×φ（xi）+b（10）

式中φ（xi）为非线性映射变量，？棕为向量和b偏移量，其次需要定义一个常量？鄣>0，设|yi-？棕×φ（xi）-b|为G，对于某个点（xi，yi），如果G≤？鄣，则完全没有损失，如果G>？鄣，则对应的损失为|G-？鄣|。则SVM回归模型损失度量为：

err（xi，yi）=   0        G≤？鄣G-？鄣    G>？鄣（11）

在回归模型中，设立优化目标函数可以与分类模型相同为||w||2，根据设定的损失函数度量，则最终损失函数S为：

S=C×■×∑n   i=1err（xi，yi）+■||w||2（12）

其中C是支持向量回歸的复杂度常数，表示对错误分类的容忍度，其中较高的C值产生“较软”的边界，较低的值产生“较硬”的边界。在核函数的选择上LIBSVM包常采用RBF核函数，RBF核函数适用于特征数量远小于样本数量的数据集。

Kradial（xi，yi）=e-■∑p   k=1（xik，xjk）2（13）

三、数据预处理及模型评估方法

1.数据

实现GLM、Deep Learning、GBT、SVM四种预测模型进行对比分析，以某高校计算机与通信工程学院下计算机科学技术专业2015级、2016级、2017级三个年级的大二上、下两个学期的10门考试课程为实验数据。由于高校课程的多样性，遂剔除学生的选修课程和考查课程。数据集中课程属性可以分为专业课程和公共课程，其中专业课程包括计算机组成原理、数据库原理、面向对象程序设计、数据逻辑分析与设计、计算机网络、数据结构;公共课程包括大学物理、大学英语读写译Ⅲ、大学英语读写译Ⅳ、马克思主义基本原理。

2.数据清洗及预处理

由于从教务数据库中抽取的数据并不能直接应用于预测模型，需要对抽取的数据进行清洗转换来满足模型预测要求的数据集，遂对数据做如下操作：

（1）数据清洗：运用Pentaho kettle数据仓库软件进行数据清洗。将教务抽取的数据按照年级划分成三个子集，对每个子集进行特征筛选、数据去重操作，并将数据进行行列转换形成满足模型需求的数据集样式，最终按照学号将三个子集合并成最终预测数据集。

（2）缺失值处理：对数据集进行简单描述性分析，查看数据是否存在缺失值。学生课程数据的缺失由学生休学、调换专业等人为因素组成，且在数据集中占比极小，遂对缺失成绩样本进行剔除。

（3）建立训练样本：将样本数据的60%作为训练样本，另外40%作为测试样本。

3.模型评价指标

文章从预测精度、模型适用性两个角度对GLM、Deep Learning、GBT、SVM四种预测模型进行评价分析：

（1）预测精度：不同模型的预测结果的评价指标有均方根误差（RMSE）、平均绝对误差（MAE），RSEM用来衡量预测值与真实值之间的偏差，MAE可以更好地反映预测误差的实际情况。二者计算公式如下：

RSME=■（14）

MAE=■∑m   i=1（yi-■i）（15）

其中m为样本数量，yi为真实值，■i为预测值。

（2）模型适用性：运用模型精度和数据拟合状况，探索不同课程在不同预测模型中的预测误差的分布差异，判定模型对课程的适用性。

四、结果分析

1.预测结果对比

将四种预测模型的预测值与真实值在40%验证数据集中依照专业课程和公共课程两种属性，实现同一课程不同算法的预测结果对比，寻找四种模型的预测差异。选取专业课中数字逻辑分析与设计、面向对象程序设计，公共课程中马克思主义基本原理、大学物理共四门课程为代表进行误差分析，预测成绩与真实成绩的分布状况如图2、3、4、5所示。图中真实值是已知的，图中的每个点代表一个特定的预测值和它的真实值，黑色虚线为最优模型，图中各数据点越接近虚线——黑色虚线，预测模型越好。图中阴影区域和深色线为添加的一条平滑曲线，便于观测数据点的分布趋势。在高校教学过程中，认定学生成绩在60分以上（包含60分）为及格，依此做两条浅色虚线为辅助线，按照顺时针方向划分为四个区域，每个区域表示了不同的成绩分布属性。区域1代表了真实成绩在60分以上但预测成绩在60分以下;区域2代表了真实成绩和预测成绩都在60分以上;区域3为真实成绩60分以下且预测成绩60分以上。区域4代表真实成绩和预测成绩都在60分以下。

（1）专业课程

图2、3所示为面向对象程序设计、数字逻辑分析与设计的预测成绩与真实成绩的分布状况，在面向对象程序设计课程中GLM模型拥有最优的RSME和MAE，在数字逻辑分析与设计课程中Deep Learning模型拥有最优的RSME和MAE。图中当真实成绩小于60分时，四种模型的成绩分布回归曲线在最佳模型上方，表示预测成绩高于真实成绩;在真实成绩高于60分的区域数据分布回归曲线在最佳模型下方，表示此部分预测成绩低于真实成绩。有部分数据点远离分布的回归曲线，表明模型对这些学生的预测能力差，预测相差较大，在专业课程中预测成绩分布低于真实成绩。

（2）公共课程

图4为马克思主义原理的预测成绩与真实成绩的分布状况，在这门课程中数据分布较为集中且预测成绩几乎都超过60分，数据的回归曲线在最佳模型上方，预测成绩普遍高于真实成绩。图5为大学物理课程的成绩分布，此门课程中当真实成绩小于60分时，预测成绩全部高于真实成绩;当真实成绩大于60分时，预测成绩整体低于真实成绩，类似于专业课程。

2.预测误差分析

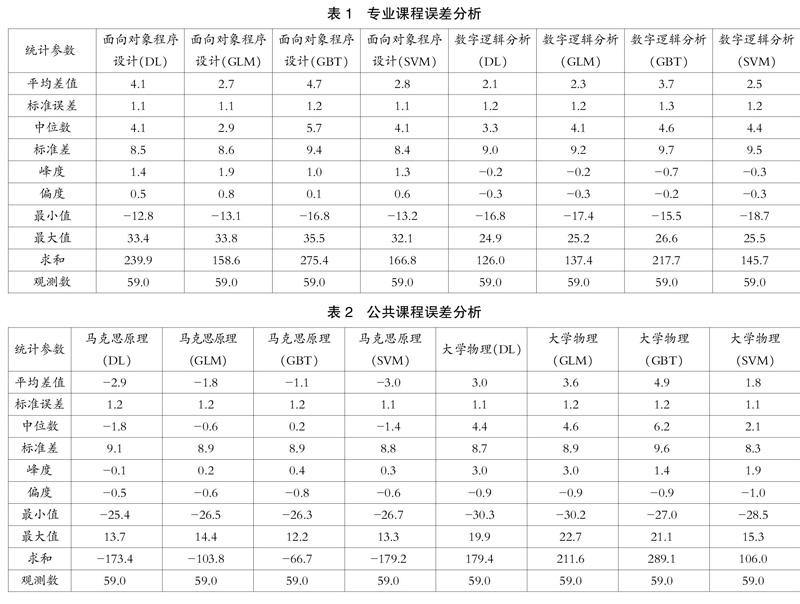
对上述四门课程的真实成绩减去预测成绩的差值进行描述性统计分析，基于误差平均值、中位数、峰度、偏度等分析误差分布的特征，两门专业课程的误差描述分析如表1所示。

在专业课程中误差均值都大于0，表明模型预测成绩均值低于真实成绩均值。各模型误差的最大值与最小值误差较大，在部分极值状况下模型预测结果不理想。在面向对象成绩设计课程中GLM模型拥有最小的平均值和中位数，该课程的误差最大值为35.5，此课程中的四种模型的峰度全部大于0，表明方差的增大是由低频度的大于或小于平均值的计算差值引起的;且此课程的偏度大于0，表明分布具有正偏离，有少数变量值很大，使右侧尾部拖长。在数字逻辑分析课程中Deep Learning模型的误差平均值和中位数最小，四种模型的峰度和偏度都小于0，表明该课程在分布上峰度不足且属于左偏态，且四种模型峰度偏度相差较小。

公共课程的误差描述分析如表2所示，在公共课程中马克思原理课程的误差均值小于0且最小值較大，表明在某些极值状况下该课程预测成绩远远高出真实成绩。马克思主义原理在GBT模型拥有最好的误差均值、标准误差和中位数，在分布状况呈现平峰和左偏态。在大学物理课程中SVM模型的误差均值、标准误差和中位数最小，误差分布产生过度的峰度且呈现左偏态。大学物理课程的误差最小值绝对值高于误差最大值，但误差总和为正数，预测成绩总体低于真实成绩。

3.预测模型精度

利用上述建立的GLM、Deep Learning、GBT、SVM四种预测模型对计算机科学与技术专业10门课程进行预测，预测模型评价指标由测试数据集进行计算验证，4种模型在相同数量的训练样本下的预测精度如表3所示。

在表3中，字体加粗倾斜代表不同课程在四种预测模型中的最优RSME和MAE。在实验样本中预测精度最好的是Deep Learning模型，其次是SVM预测模型，而GLM模型和GBT模型预测性能较为一般。在不同课程属性中，模型的适用性也有所差别。在专业课程中Deep Learning模型的预测精度更好，Deep Learning模型的RSME和MAE最优预测精度次数最多。在公共课程中SVM算法的预测精度优于Deep Learning模型，在获得最优RSME的同时MAE也是最优。

4.模型适用性建议

利用数据挖掘算法对高校学生进行回归成绩预测的过程中，Deep Learning模型在专业课程中拥有较好的预测能力，主要表现在拟合课程间相关性能力最好;而在公共课程中SVM模型拥有较好的预测能力，SVM对某些极值的预测能力优胜于其他三种模型，若采用单一算法进行回归成绩预测可以选取SVM模型。GLM在预测能力上表现一般，主要是在极值的预测能力上受到限制，若考虑在剔除部分异常的数据前提下，GLM模型在专业课程上预测能力优于Deep Learning。GBT模型在四种回归模型中性能最低，但GBT模型的运行效率最高，且模型预测成绩分布上更拟合正态分布。在学生成绩回归预测过程中，回归预测模型对学生成绩数据中的离群数据的解释能力较差，在数据预处理阶段可以剔除部分离群学生数据。

五、结语

针对常用的分类模型的成绩预测结果单一和难以分析的问题，文章采用GLM、Deep Learning、GBT、SVM四种模型进行回归成绩预测，从模型预测精度、预测成绩与真实成绩分布和误差分析进行对比分析，对各种模型在成绩预测上的适用性给出自己的见解。回归模型的成绩预测结果可以进一步实现数据统计分析，能够详细展现预测学生成绩的状况，以直观、清晰、多样的形式为教师和学校管理者提供决策支持，也能为学生学习重点提供指导，对提升学生个性化教育起到推动作用。

参考文献：

[1]周庆，牟超，杨丹.教育数据挖掘研究进展综述[J].软件学报，2015（11）：282-298.

[2]Goker H，Bulbul H I，Irmak E.The Estimation of Students' Academic Success by Data Mining Methods[C].International Conference on Machine Learning & Applications. IEEE Computer Society，2013.

[3]Francis B K，Babu S S.Predicting Academic Performance of Students Using a Hybrid Data Mining Approach[J].Journal of Medical Systems，2019，43（6）：162.

[4]刘博鹏，樊铁成，杨红.基于数据挖掘技术的学生成绩预警应用研究[J].四川大学学报（自然科学版），2019（2）.

[5]孙力，程玉霞.大数据时代网络教育学习成绩预测的研究与实现——以本科公共课程统考英语为例[J].开放教育研究，2015（3）.

[6]张慧玲，高小力，刘永前等.三种主流风电场功率预测算法适应性对比研究[J].现代电力，2015（6）：7-13.

[7]李靜，徐路路.基于机器学习算法的研究热点趋势预测模型对比与分析——BP神经网络、支持向量机与LSTM模型[J].现代情报，2019（4）：24-34.

[8]H2O.ai.H2O-3框架使用说明[EB/OL].http：//docs.h2o.ai.

[9]Kumar K B S，Krishna G，Bhalaji N，et al.BCI cinematics-A pre-release analyser for movies using H 2 O deep learning platform[J].Computers & Electrical Engineering，2018：S0045790617315318.

[10]林鹏程.预测锂电池充电时间的三段SVR模型[J].电源技术，2018（8）：67-69，144.

[11]陈德鑫，占袁圆，杨兵.深度学习技术在教育大数据挖掘领域的应用分析[J].电化教育研究，2019（2）：70-78.

（编辑：王天鹏）