合肥市二手房成交价格研究
2020-11-02刘海
刘海


摘要:二手房交易市场比重的增大,使得对于二手房房价预测构建模型有重要意义。选取合肥市2019年6月至2020年6月的二手房成交记录作为研究数据。针对BP神经网络模型易陷入局部最优和传统遗传算法的BP神经网络收敛速度过慢的不足,建立双链遗传算法的BP神经网络模型,对研究数据进行仿真训练,并检验了模型的泛化能力。实验结果表明使用模型在精度和收敛速度的双重考量下最优。
Abstract: The increasing proportion of the second-hand housing market makes it important to build a model for the prediction of second-hand housing prices. This paper selects the transaction records of second-hand houses in Hefei City from June 2019 to June 2020 as the research data. The BP neural network model is easy to fall into the local optimum and the convergence speed of the traditional Genetic Algorithm is too slow. In this paper, the BP neural network model of Double-chain Genetic Algorithm is established, the research data are simulated and trained, and the generalization ability of the model is tested. The experimental results show that the proposed model is optimal under the consideration of both accuracy and convergence speed.
关键词:房价预测;BP神经网络;遗传算法;双链遗传算法
Key words: house price forecast;BP neural network;Genetic Algorithm;Double-chain Genetic Algorithm
中图分类号:F224 文献标识码:A 文章编号:1006-4311(2020)29-0003-04
0 引言
近年来中国房地产行业发展迅速,人们买房的需求不断增加,使得房屋交易由新房交易为主逐步转变成新房和二手房交易“并驾齐驱”[1]。因此建立模型能够对二手房房价进行一房一价预测在交易中有重要的参考价值。
在机器学习算法中BP神经网络由于具有良好的泛化能力、学习能力和映射能力,使得其在房价预测中有一定的优势[2-4]。然而BP神经网络在训练过程容易使模型参数收敛为局部极值,无法达到最优,所以将遗传算法(GA)与BP神经网络模型进行组合,补足了神经网络的缺点[5]。李春生、李霄野[6]等用遗传算法改进BP神经网络,对中国2005年至2015年的房价进行研究,发现改进后的算法比单一的BP神经网络的性能更好。杭晓亚、柳叙丰[7]等运用GA-BP模型对青岛市的房价进行预测,效果也十分显著。但是传统的遗传算法存
在收敛过慢或早收敛现象[8],因此使用双链遗传算法优化BP神经网络建立模型对合肥市二手房房价进行预测研究。
1 BP神经网络和双链遗传算法
1.1 BP神经网络
BP神经网络(Back Propagation Network)是一种通过误差反向传播进行参数调优的多层前馈神经网络,是运用最普遍的神经网络模型[9]。模型由输入层、隐含层、输出层组成,且各层神经元之间采用全连接形式[10]。一个隐含层的BP神经网络拓扑结构如图1所示。
BP神經网络的训练过程由信号的正向传播和误差的反向传播构成。正向传播时,信号由输入层进入网络,通过隐含层的信号处理后将信号传入输出层,当输出层输出与期望输出之间的误差满足预设精度则模型训练终止,否则进入误差反向传播阶段;反向传播时,通过梯度下降法优化目标函数将误差反向传向各层,对各层每个神经元的权值和阈值进行调整[11]。信号的正向传播和误差的反向传播更替进行,直到误差精度达到预设要求或者迭代至预设的次数。
1.2 双链遗传算法
遗传算法(Genetic Algorithm,GA)是基于达尔文进化论的思想提出的一种优化搜索计算模型,通过模拟自然界物种在繁衍后代过程中个体的选择、基因的交叉、变异,将优良基因保留而淘汰劣质基因的原则实现对问题解的优化[12]。传统的遗传算法在对个体进行编码时采用的时单链染色体结构,本文使用了一种改进算法,引入更符合自然界遗传规律的双链染色体结构[13-14],称之为双链遗传算法(Double-chain Genetic Algorithm,DGA)。
1.2.1 染色体的双链结构
双链遗传算法中每个个体有两条染色体,含有两份相同的遗传信息,在进行遗传操作时通过解链只对其中的一条染色体进行交叉、变异产生子代染色体,使得既能参与遗传进化生成子代基因,又能保留父代潜在的优秀基因,使得迭代进行的遗传操作时,增加种群的多样性,扩大了搜索空间[15-16]。
1.2.2 双链染色体遗传操作
Step1:对需要优化的问题进行编码处理;
Step2:初始化种群X0,设定最大遗传代数G,初始遗传代数g=0;
Step3:计算初始种群个体X0每条链适应度值;
Step4:对初始种群中个体进行选择、交叉、变异操作产生新的个体Xg,此时种群中新个体的双链染色体中既包含父代信息基因链也包含子代信息基因链;
Step5:计算新个体Xg中父代链和子代链的适应度值,将适应度值更优的基因链代入下一次遗传操作中,直到g=G时结束。
2 数据来源及数据预处理
2.1 数据来源
本文使用的数据来自链家二手房网(https://hf.lianjia.com),采集2019年6至2020年6月合肥市二手房成交数据,共得到12581条有效数据。其中每条数据含有特征变量28个,对特征变量进行分类,分为3个类型,分别为数值变量、名义变量和序数变量。具体变量如表1所示。
2.2 原始变量的衍生
在链家网上收集到的房屋户型数据的具体形式有2室1厅1厨1卫、3室1厅1厨2卫等52种形式,若按照处理名义变量的方式来处理此变量,易导致维度灾难,因此本文根据房屋户型变量的数据特征,将其衍生出卧室数量、厨房数量、客厅数量、卫生间数量4个数值变量。
在链家网上收集到的梯户比例数据的具体形式有2梯4户、1梯2户、1梯4户等155种形式,按照处理名义变量的方式来处理也会造成维度灾难,因此构造新的梯户比例:梯数与户数的比值。
2.3 数据的预处理
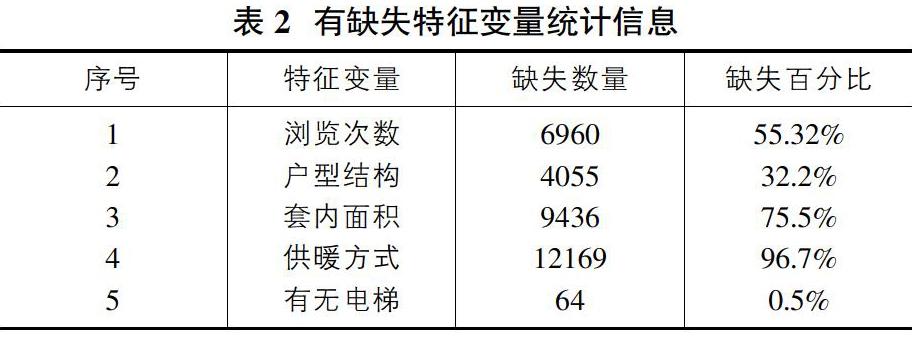
原始数据中可能含有大量的缺失值和异常值,不利于对数据的分析以及后续的建模,为了提升原始数据的质量以便后续工作的进行,需要对数据进行预处理。本文首先对数据的缺失值进行处理,表2展示了有缺失值的特征变量的统计信息。
表2展示了原始数据中部分特征变量的缺失信息。其中浏览次数、套内面积、供暖方式缺失比例分别为55.32%、75.5%、96.7%,缺失比例过大,因此将这三个变量直接删除;有无电梯缺失比例小于1%,因此将缺失的记录删除;户型结构缺失比例为32.2%,采用众数插补的方式对缺失值进行补充。
对原始数据缺失值进行处理之后在对数据的异常值进行处理,本文通过箱线图、经验判断的方式对异常值进行检测,并删除异常值。
2.4 数据量化处理
接着对名义变量和序数变量进行量化处理。其中名义变量采用one-hot编码处理。
序数变量为所在楼层,取值为低、中、高,可分别取值为0、1、2。
为消除数值变量量纲的影响,将数值变量进行归一化,归一化的公式为:
其中xstd为归一化后的数据,xmin和xmax分别为每个数值变量的最小值与最大值。
至此完成对数据的处理,下面将处理后的数据用于建模。
3 DGA-BP二手房成交价格预测模型
3.1 DGA-BP模型参数设置
DGA-BP模型设置的参数分为BP神经网络参数设置和双链遗传算法参数设置,设置具体如下:
①确定BP神经网络模型的基本结构。确定BP神经网络的隐含层层数及各层神经元个数。设定神经网络输入层有54个神经元,1个隐含层且隐含层神经元有109,输入层有1神经元。同时通过多次调整确定BP神经网络的学习率为0.01,预设迭代次数为30000次。
②设定适应度函数,用于计算种群中个体的适应度。本文使用测试集误差本文使用BP神经网络测试集的测试误差作为适应度函数,适应度函数为:
yi为测试集中数据的真实值,i为数据的估计值。
③设定最大遗传代数,初始化种群,随机产生一个初始种群,将种群中每个个体通过格雷编码的方式进行编码,每个个体含有两条信息相同的染色体,都含有神经网络权值和阈值的全部信息,并计算初始种群中每个个体的每条链的适应度值。本文设定种群规模为50,最大遗传代数为200。
④进行遗传操作設定:
选择算子:本文采用轮盘赌的方式进行选择操作;
交叉算子:本文采用两点交叉的方式进行交叉操作;
变异操作:本文设定的变异概率为0.01。
3.2 模型评价指标
①平均绝对误差(MAE)。平均绝对误差是期望值与预测值差值的平均值。计算公式如下:
其中n为样本数目,yi为期望值,i为估计值。
②均方误差(MSE)。均方误差是期望值与预测值差值平方的平均值。计算公式为:
其中n为样本数目,yi为期望值,i为估计值。
③可决系数(R2)。可决系数是判定模型拟合能力的指标,可决系数越大则模型的拟合能力越强。其计算公式如下:
式中:SSE为回归平方和;SST为总离差平方和;SSR为残差平方和,其计算公式如下:
其中yi为样本的期望值,yi为样本的平均值,i为样本的估计值。
3.3 实验结果
本文使用有效数据9817条数据,按照3:7的比例将数据集划分为测试集与训练集,通过与BP神经网络和传统的GA-BP模型进行比较,突出本文使用的DGA-BP模型的优越性。
其中图2表示DGA-BP模型在收敛速度上与GA-BP模型的比较结果。从图中可以看出DGA-BP模型的收敛速度远远快于GA-BP模型,在进化到53代时就达到最佳收敛,收敛速度远远快于GA-BP模型。
表3表示了BP模型、GA-BP模型、DGA-BP模型在测试集上的计算结果的展示,从表中可以看出在MAE、MSE、R2指标的测度中,GA-BP模型和DGA-BP模型的计算结果都优于BP模型。
从上述叙述中可以总结得出DGA-BP模型在收敛速度和算法精度的综合考量中最优,于此同时新抓取了合肥市二手房成交数据800条,使用DGA-BP模型进行拟合,得出其MAE为784、MSE为787652、R2为0.9123。其前100个数据拟合结果展示如图3所示,通过新抓取数据的验证,可以看出DGA-BP模型能够对合肥市二手房成交价格进行较好的预测。
4 结论
本文通过采集合肥市2019年6月至2020年6月城区二手房成交记录数据,对比传统BP神经网络模型和GA-BP模型,建立一种能够对二手房成交价格进行有效预测的DGA-BP模型,该模型弥补了BP模型和GA-BP模型的不足,使得在追求模型收敛速度和预测精度的双重考量为最优选择。在进化到54代时,对测试集进行拟合,可决系数R2为0.9406,对新抓取数据的拟合,可决系数为0.9123。说明模型有较好的泛化能力。
然而在建模时将搜索到的所有指标都投入模型中,没有考察变量的有效性从而对指标进行筛选,使得本文建立的模型未能最简化,也降低了模型的收敛速度。今后对如何在众多指标中筛选中稳健的重要指标是研究的一个方向点。
参考文献:
[1]姜沛言,孙聪,刘洪玉.住房市场研究中的样本城市选择[J].统计与决策,2016(05):29-33.
[2]李广胜,郭欢.基于GM(1,1)模型的南京市房价预测研究[J].江汉大学学报(自然科学版),2020,48(02):10-13.
[3]高文,李富星,牛永洁.基于BP神经网络对房价预测的研究[J].延安大学学报(自然科學版),2018,37(03):37-40.
[4]王筱欣,高攀.基于BP神经网络的重庆市房价验证与预测[J].重庆理工大学学报(社会科学),2016,30(09):49-53.
[5]张立毅,刘婷,孙云山,李锵.遗传算法优化神经网络权值盲均衡算法的研究[J].计算机工程与应用,2009,45(11):162-164.
[6]李春生,李霄野,张可佳.基于遗传算法改进的BP神经网络房价预测分析[J].计算机技术与发展,2018,28(08):144-147,151.
[7]杭晓亚,柳叙丰,赵泽昆.基于GA-BP神经网络的青岛房价预测[J].四川建筑,2015,35(06):233-236.
[8]PHOLDEE N, BUREERAT, S. Hybrid real-code population-based incremental learning and approximate gradients for multi-objective truss design[J]. Engineering Optimization, 2014, 46(8):1032-1051.
[9]李英冰,陈雨劲,欧阳茜.基于BP神经网络的武汉市二手房估价模型研究[J].数字制造科学,2017,15(Z1):66-70.
[10]严旭,李思源,张征.基于遗传算法的BP神经网络在城市用水量预测中的应用[J].计算机科学,2016,43(S2):547-550.
[11]任谢楠.基于遗传算法的BP神经网络的优化研究及MATLAB仿真[D].天津师范大学,2014.
[12]李岩,袁弘宇,于佳乔,张更伟,刘克平.遗传算法在优化问题中的应用综述[J].山东工业技术,2019(12):242-243,180.
[13]刘金山,廖文和,郭宇.基于双链遗传算法的网络化制造资源优化配置[J].机械工程学报,2008(02):189-195.
[14]Harsh Bhasin, Gitanshu Behal, Nimish Aggarwal, Raj Kumar Saini, Shivani Choudhary. On the applicability of diploid genetic algorithms in dynamic environments[J]. Soft Computing, 2016, 20(9).
[15]吴家宏,雷毅.基于双螺旋染色体和分层结构的遗传算法[J].计算机集成制造系统,2005(12):1743-1746.
[16]谢承旺,王志杰,魏波,徐君,汪慎文.一种双链结构的多目标进化算法DCMOEA[J].控制与决策,2015,30(04):577-584.
