两挡纯电动汽车动力总成悬置系统优化设计

刘成强,徐海港,张建武，林连华

(1. 山东时风(集团)有限责任公司，山东 聊城 252800；2.上海交通大学 机械与动力工程学院，上海 200240)

目前，驾驶员和乘客对电动汽车的电驱动动力总成在行驶过程中的NVH(noise, vibration, harshness)性能提出了更高的要求。车架与动力总成之间的悬置系统具备两个作用，即不平衡激励的振动隔离和驱动力矩的平衡约束。悬置系统对隔离驱动电机的周期性转矩波动和变速器的啮合激励，以及对车辆的减振、降噪起到了重要作用，因此，悬置系统对提升电动汽车的电驱动性能具有重要的作用。

目前对动力总成悬置系统的研究主要集中在传统的内燃机车辆，分为对悬置系统与动力总成耦合的固有特性分析和对悬置刚度的优化设计两个方面。文献[1-4]分析了动力总成的固有特性，采用能量解耦方法对悬置系统进行了固有频率和能量分布的优化；文献[5-6]采用多目标优化算法，综合考虑了发动机的怠速工况、动力总成的变形以及系统的能量解耦率要求，对发动机悬置系统进行了稳健和优化设计；Liu 等[7]提出了三缸发动机的动力总成悬置系统设计要求及方法。为研究路面激励引起的悬置系统的振动，Shangguan等[8]建立了13自由度动力总成-车身-非簧载质量模型，给出了悬置动刚度和阻尼的确定原则。然而对于纯电动汽车而言，驱动电机与发动机的激励特性存在很大差异，因此有必要在以上研究的基础上，综合考虑电机的电磁转矩激励和变速器齿轮的动力学特性，针对性地研究纯电动车辆的悬置系统与动力总成耦合的固有特性和对悬置刚度的优化设计。在国内，岳巍等[9]进行了电动汽车动力总成悬置可靠性验证研究，在动力总成系统级阶段,使用六自由度振动台和扭转作动器,验证动力总成悬置可靠性,在车型的开发前期及时发现设计问题, 为动力总成可靠性优化提供试验数据支持；朱鑫等[10]根据纯电动汽车和内燃机汽车在动力总成激励上的不同，建立某型纯电动汽车动力总成六自由度动力学模型，以动力总成固有频率和能量分布合理分配为优化目标，各个悬置静刚度和安装位置为设计变量，应用Matlab/Isight对悬置系统参数进行优化；王海波[11]通过对汽车动力总成振动的分析,探讨悬置系统的工作原理,为建立隔振实验模型提供理论基础。在国外，Tao等[12]采用分数阶导数模型建立了液压悬置的动态特性模型，并通过试验确定了模型参数；Barszc等[13]采用集总参数模型对多惯性通道半主动悬置进行了分析，推导了惯性通道参数与液柱谐振频率的关系，并进行了试验验证。本文也将在此基础上，对两档纯电车动力总成悬置系统进行优化设计。

本文采用三点式悬置策略的动力总成悬置系统，这三个悬置件分别安装于双速变速器的前、后端，以及驱动电机尾端。通过Adams建立了六自由度的动力总成悬置振动模型，进行了系统模态和能量解耦率的分析。在综合测试工况下，对动力总成悬置系统的质心位移作了计算，并采用粒子群算法(PSO-GA)对悬置系统的能量解耦率进行了优化。计算结果表明，优化后的悬置系统的固有频率、能量解耦率和质心位移等设计指标均能满足技术要求。

1 纯电动汽车动力总成悬置系统建模

为便于分析，在振动分析中将3个橡胶悬置件简化为弹簧。把动力总成与悬置系统等效成1个六自由度刚体与3个三维弹簧。悬置系统分析涉及3个坐标系：

整车坐标系：以整车质心为坐标系原点，选取汽车行驶方向的相反方向为X轴，汽车前进方向的右侧为Y轴，根据右手定则确定Z轴。

动力总成坐标系：以动力总成质心为原点，X轴和汽车前进方向相反，曲轴中心线方向为Y轴，根据右手定则确定Z轴。

悬置系统坐标系：以3个弹簧的弹性中心为原点，弹性主轴方向为坐标轴方向。

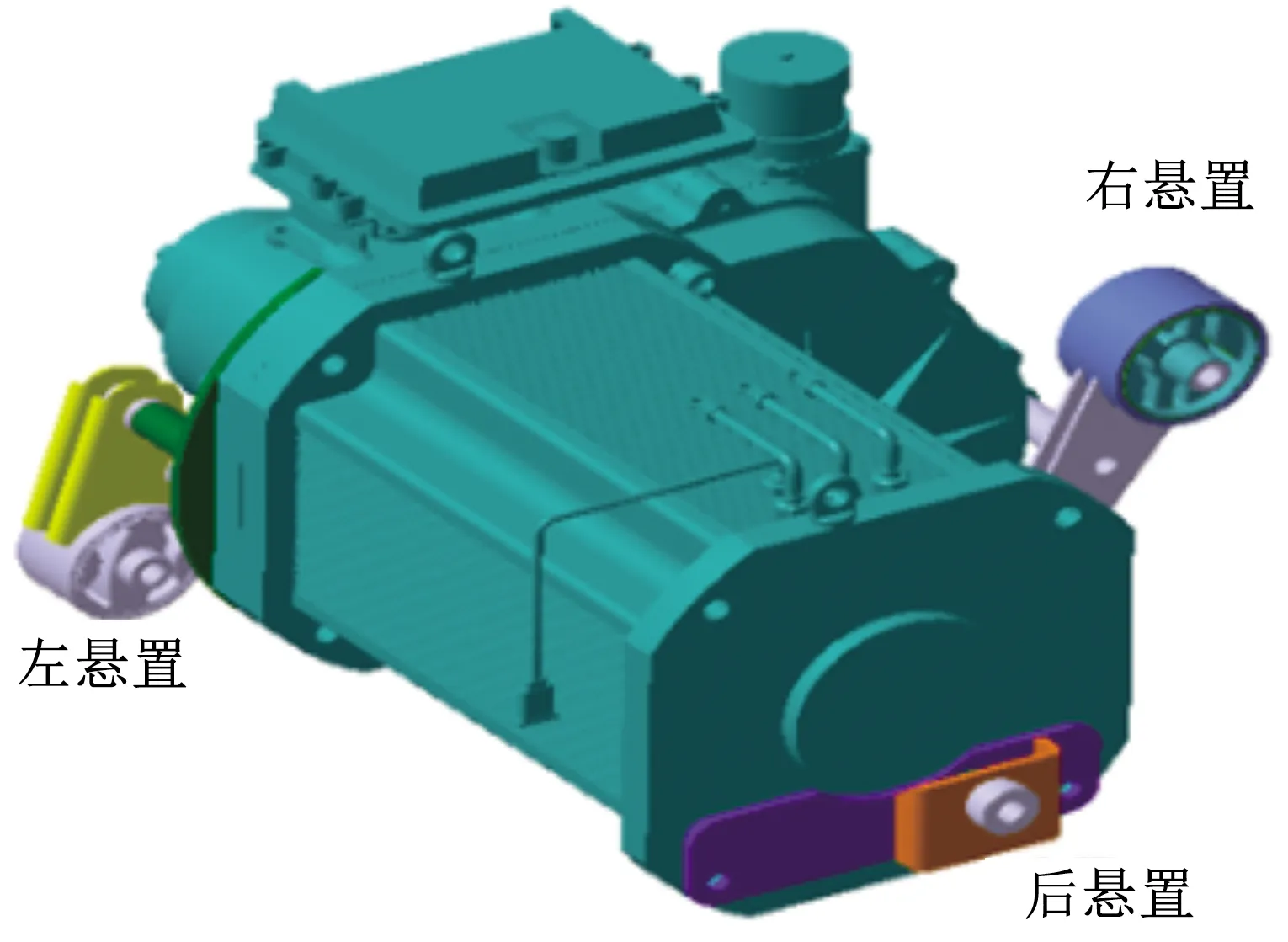
图1 动力总成与悬置系统Fig.1 Powertrain and mount system

表1 动力总成惯性积及质心位置Table 1 Inertial product and gravity center positions of powertrain

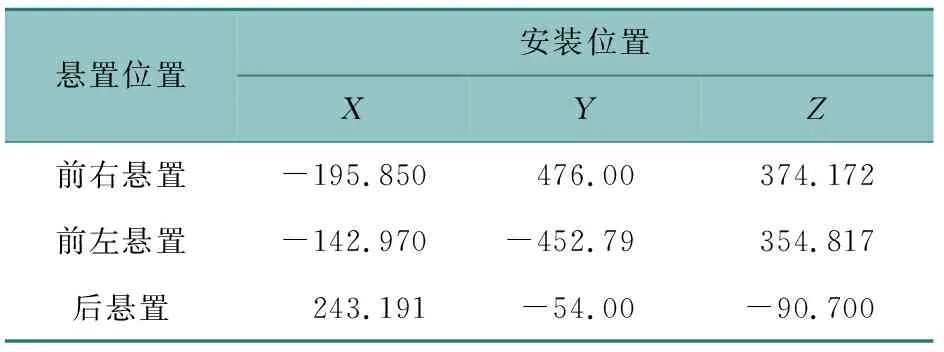
表2 动力总成3个悬置件安装位置Table 2 Installation positions of the three mounts for the powertrain 单位：mm

表3 动力总成3个悬置件的刚度Table 3 Stiffness of the three mounts for the powertrain 单位：N·mm-1

控制六自由度动力总成悬置系统平衡的拉格朗日方程如下：

(1)

其中ET、EV和ED分别是系统的动能、势能和耗散能；q为系统的广义坐标；Q为广义力。

系统振动的固有特性分析不涉及外力，并忽略悬置阻尼的影响，经推导和简化，悬置系统的自由振动平衡方程为：

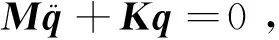
(2)

其中质量矩阵M为：

系统刚度矩阵K为：

悬置刚度Ki为：

位移转置矩阵Bi为：

方向转移矩阵Ti为：

2 动力总成悬置系统仿真分析

应用Adams软件建立悬置系统的六自由度振动模型，假设整车车身为地(ground)，动力总成为刚体，3个悬置件则用bushing元件代替。所建模型如图2所示。采用Adams/Vibration模块，计算动力总成悬置系统的固有振动特性，结果如表4所示。

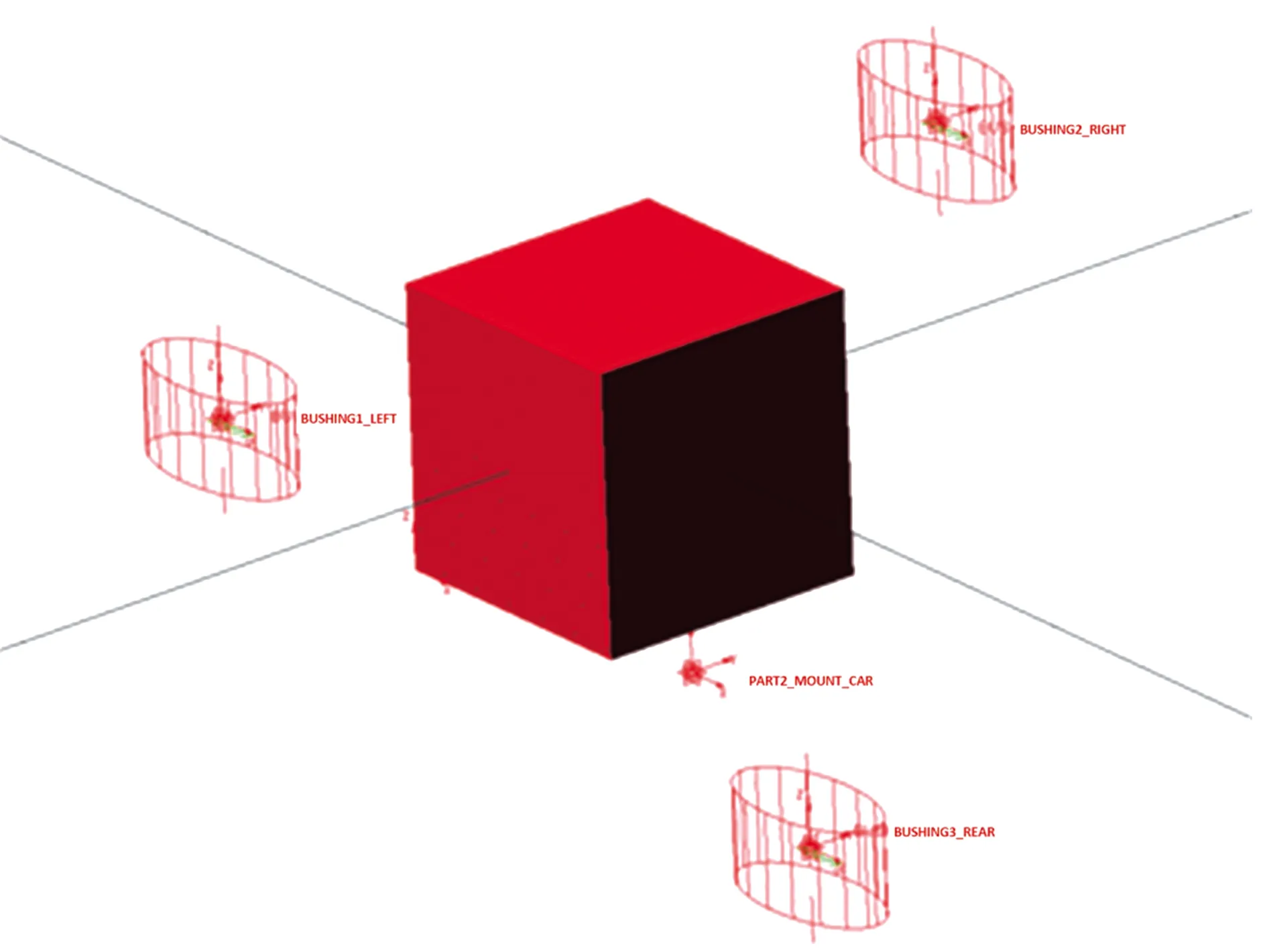
图2 动力总成与悬置系统的Adams建模Fig.2 Adams model of the powertrain and mount system

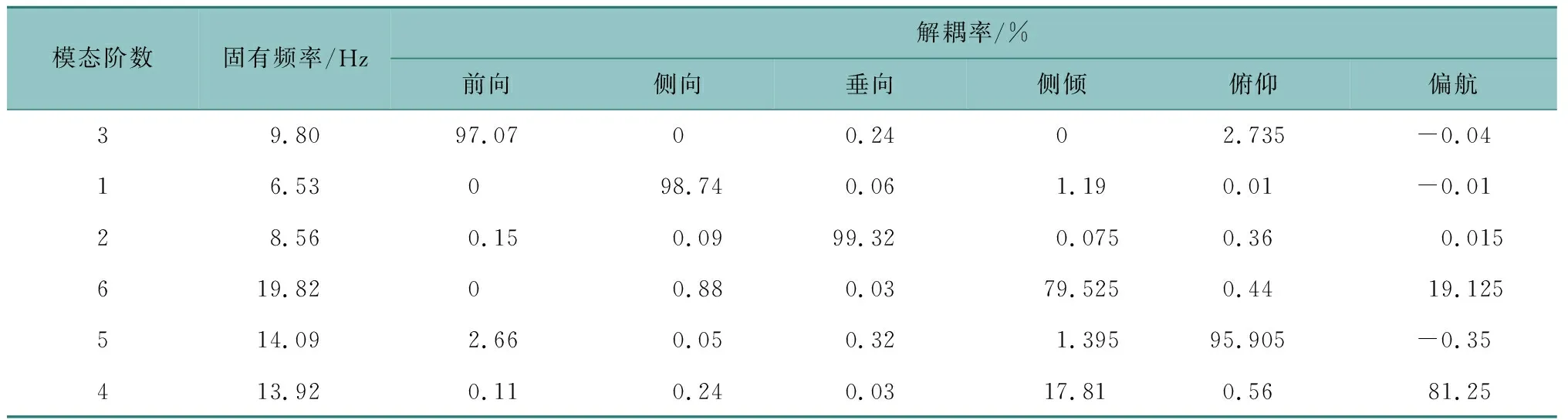
表4 优化前悬置系统的模态分析计算结果Table 4 Numerical results for modal analysis of the mount system prior to optimization

从解耦率来看，前向、侧向、垂向和侧倾运动解耦程度都比较高，超过90%，基本实现解耦。但是，原系统在前倾和转弯方向上解耦率只有80%左右，并不理想，应对其进行改进设计。从固有频率来看，第4和第5阶固有频率之间相差不足1 Hz，极易引发模态共振，有必要加以改进。为直观起见，图3给出了系统模态振型的仿真结果，每个固有频率都对应一个振型。

图3 悬置系统各阶模态振型Fig.3 Modal shapes of the mount system

不考虑阻尼和外力，在Matlab中建立悬置系统振动平衡方程：

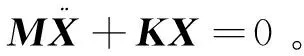
(3)

假定方程的解为X=Aejωt，将其代入式(3)可得方程如下：

(K-ω2M)A=0。

(4)

利用Matlab中求解矩阵特征值和特征向量的命令eig(K,M)，能够计算悬置系统的固有频率和振型。再利用得到的固有频率和主振型可以进行模态解耦率计算。

第k个广义坐标上分配到的动能为

(5)

其中，ωi为第i阶固有频率；(Ai)k和(Ai)l为的第i阶主振型Ai的第k个元素和第l个元素。

第k个广义坐标上分配到的能量占系统总能量的比值为

(6)

利用Matlab编程，得到的固有频率和解耦率与Adams仿真结果一致。这证明了所采用方法的正确性。

3 动力总成悬置系统优化

由于电动车不同于传统汽车，不需要考虑怠速工况。在优化时一般要达到以下几点要求：

(1)系统固有频率分布间隔大于1 Hz；

(2)能量解耦率达到90%；

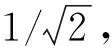
3.1 解耦率算法目标函数

为提高悬置系统解耦率，将其作为优化设计目标。在6个广义坐标所对应的主振动能量分布值矩阵中，系统解耦率可以表示为每个广义坐标下的最大能量分布值的最小值，该最小值与系统解耦率呈正相关关系。因此提高系统解耦率的算法目标函数定义为最大化上述最小值，而具体算法中目标函数表示如下：

f=min[-min(max(Tpi),i=1，…，6)],

(7)

其中，max(Tpi),i=1，…，6为广义坐标对应的主振动能量分布值。

3.2 悬置系统优化设计约束条件

悬置系统的刚度、安装位置、安装角度等因素都会影响到系统固有特性。但是考虑到成本，而且悬置元件的位置一般不轻易更改，本文选取悬置的主轴刚度作为设计变量，即kui,kvi,kwi。

悬置系统优化设计的约束条件如下：

(1)固有频率约束：fmin>5 Hz，fmax<35 Hz，相邻固有频率间隔>1 Hz

(2)悬置主轴刚度约束：悬置刚度过大不利于隔振性，刚度过小则悬置太软，导致动力总成和悬置位移变化大，容易造成运动干涉。设计主轴刚度上下限为

(3)解耦程度约束：各自由度解耦率≥90%。

3.3 PSO-GA混合算法

常用的优化算法有遗传算法(GA)和粒子群优化算法(PSO)。虽然GA和PSO都有很好的优化效果，但是也都存在自己的弱点。例如，在GA算法中，未被选择的个体信息会丢失，到了进化后期由于基因缺失，算法会早熟收敛于局部优化解，全局寻优效果较弱。虽然变异过程会给种群引入新的基因信息，但是由于变异概率很低，仅靠变异、增加进化代数引入新基因会导致算法效率低下。而在PSO中，因为所有个体最优值和全局最优值信息都被保留，全局寻优能力强，可以避免早熟的问题。但是PSO没有适者生存的选择功能，因此又会浪费资源给不适合的个体。

为了提高算法的效率和效果，本文使用编写PSO-GA混合算法的方法进行优化，在PSO算法的基础上给每个迭代中引入GA的选择、交叉、变异因子，择优选择特定数量的粒子，提高算法效率。

3.4 算法优化前后结果对比

如图4所示，首先利用unifrnd函数创建初始种群和个体速度。再将式(7)中的目标函数和约束条件结合得到适应度函数；其中，约束条件的处理是通过惩罚函数实现的，对不满足约束条件的个体进行惩罚，使其适应度值变大，遗传到下一代的概率变小。然后按照适应度值计算更新初始种群全局和个体最优解，每个粒子根据自我经验(个体最优解)和种群交流(全局最优解)调整运动方向和速度以靠近最优值。粒子群调整优化过程可以表示为如下公式：

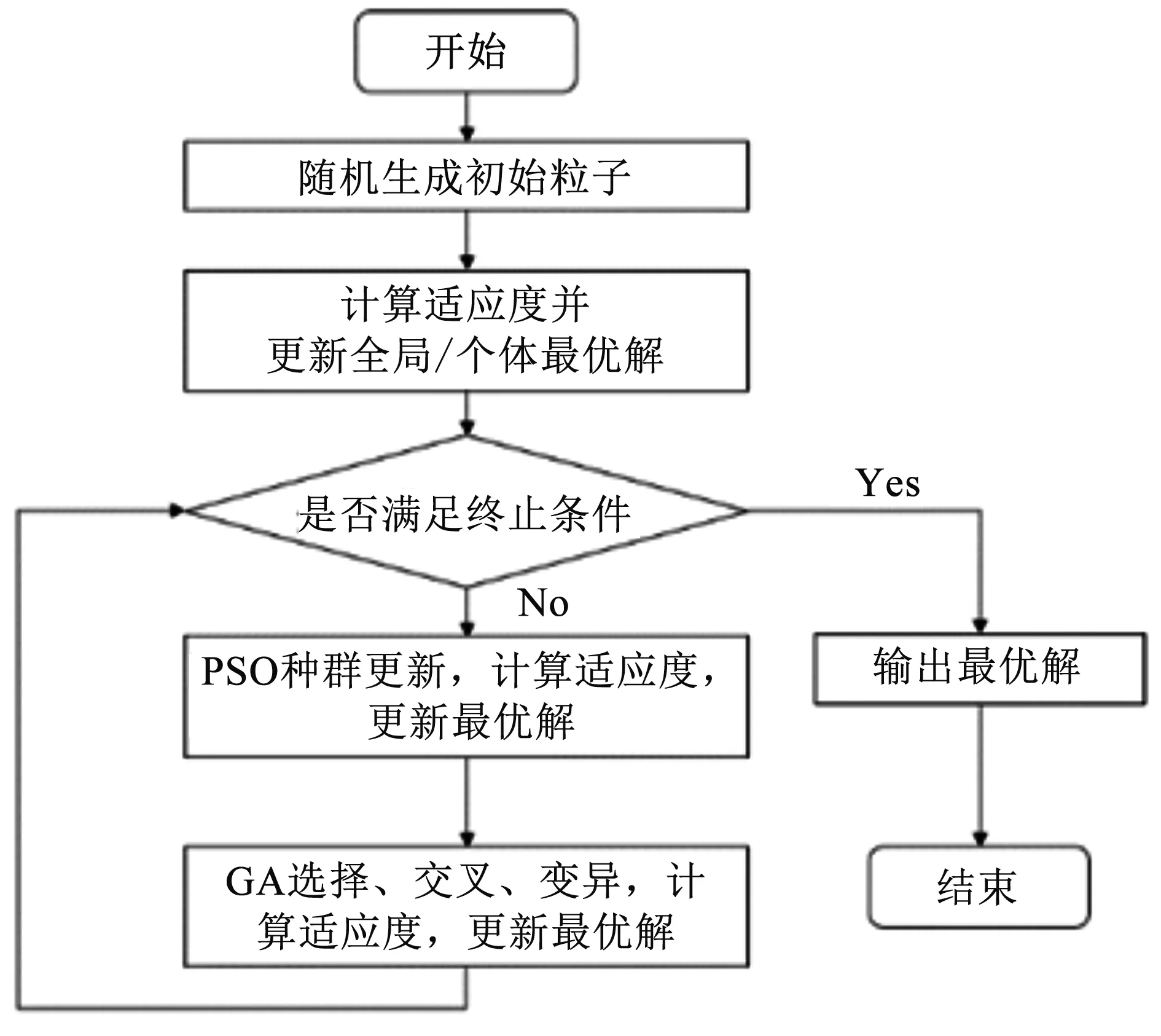
图4 PSO-GA优化算法流程Fig.4 Optimized procedures of the PSO-GA algorithm

Vi(j,k)=wVi-1(j,k)+c1γ1(Pi-1*(j,k)-Pi-1(j,k))+c2γ2(G*-Pi-1(j,k))

(8)

Pi(j,k)=Pi-1(j,k)+Vi(j,k)

(9)

其中i=1,…,50为种群代数；j=1,…,3000为种群大小；k=1,…,9为个体长度；V表示为粒子群速度；P表示为粒子群；w为惯性权重；c为学习因子；γ为随机数；P*为每代最终粒子群；G*为每代最优个体。

经过以上处理，再利用select，cross和mutation函数对父辈进行选择、交叉和变异运算，得到下一代种群。这相当于嵌入遗传优化算法对于局部区域进行优化。如此重复上述循环，直到达到初始设定的最大遗传代数，获得优化结果。

利用Matlab编写优化程序，运行结果如图5所示。

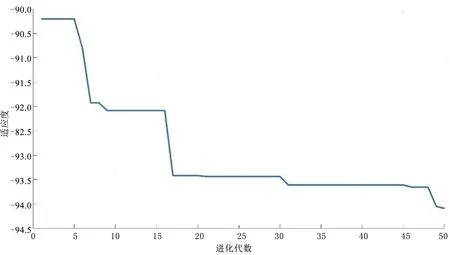
图5 适应度进化曲线Fig.5 Fitness evolution curve

优化前后主轴刚度见表6，优化后模态分析见表7，各个方向解耦率达到94%以上，固有频率也满足电动车配置要求。

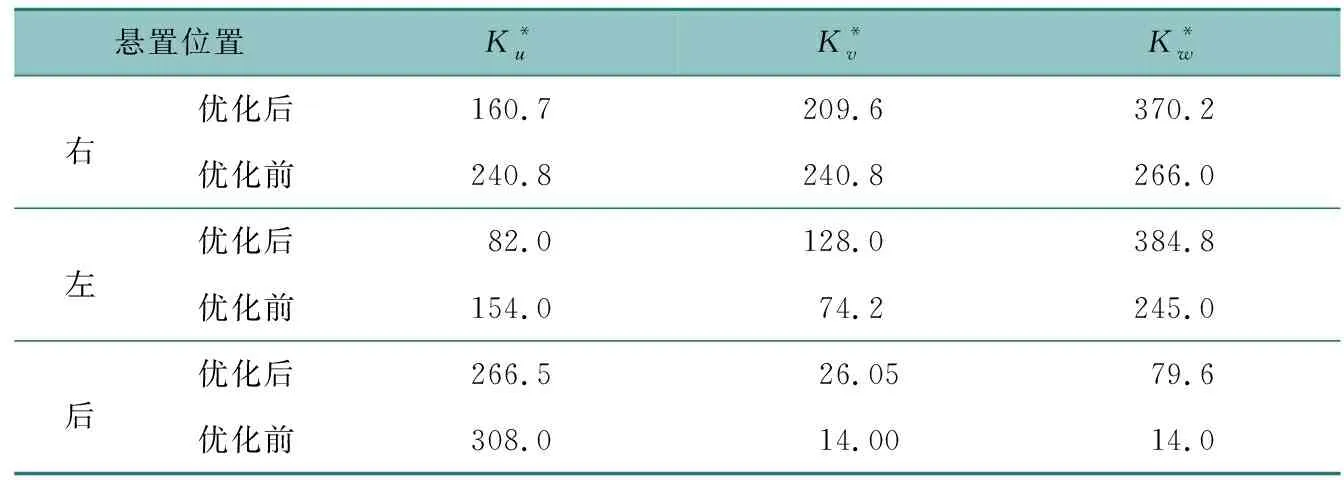
表6 优化前后悬置主轴刚度Table 6 Mount stiffness prior and subsequent to the optimization 单位：N·mm-1

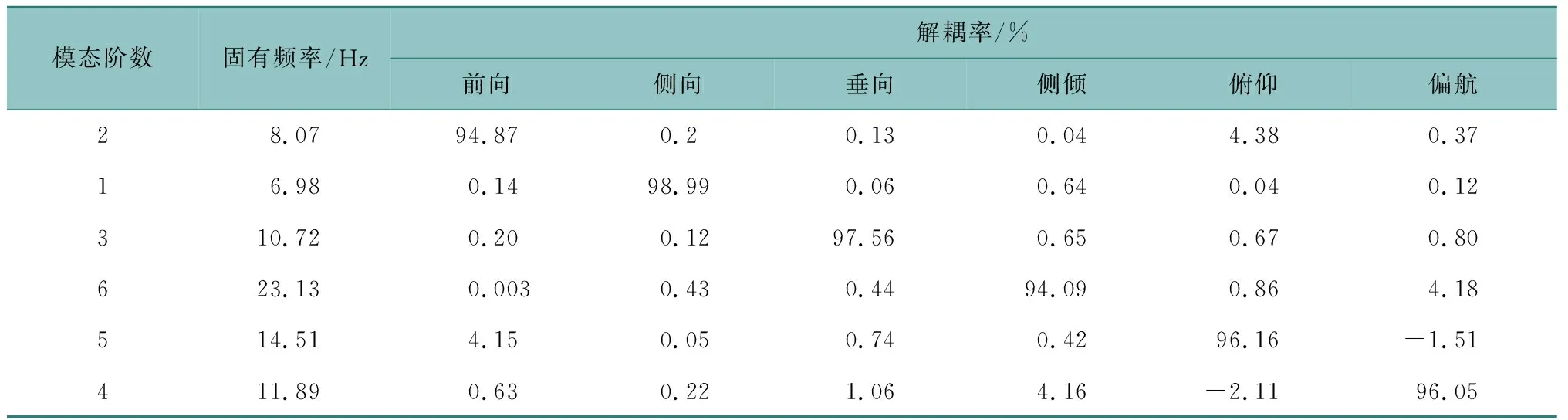
表7 优化后模态分析结果Table 7 Results of the modal analysis subsequent to the optimization

4 结语

本文利用拉格朗日原理和Adams建立电驱动2AMT动力总成悬置系统的六自由度振动模型，并进行了模态分析和动态仿真。通过采用粒子群算法和遗传算法(PSO-GA)的混合算法，对3个悬置刚度进行了优化，提高了悬置系统的解耦率。优化后模态分析结果显示各个方向解耦率达到94%以上，且悬置系统的固有频率配置也有了较大提高。因此，PSO-GA混合算法在悬置系统匹配分析中具有较强的适应能力，能够很好地解决悬置件的优化设计问题。