流动天然气管道内壁热交换系数的计算方法研究
2020-11-02张彬华路永新王世清徐学利王洲
张彬华,路永新,王世清,徐学利,王洲,2
(1.西安石油大学材料科学与工程学院,陕西 西安 710000;2.西部管道新疆输油气分公司,新疆 乌鲁木齐 830000)
天然气长输管道在服役期间,由于使用环境、运行时间等影响,易产生管道管壁减薄或局部腐蚀泄漏问题,会引起安全事故,造成严重的影响。为避免和防止管道泄漏事故的发生,通常采用套筒对重点减薄或泄露区域进行补强。但在焊接时,因管内天然气的流动而加快了套筒角焊缝热影响区的冷却速度,使得角接环焊缝热影响区会产生冷裂纹,则更容易发生失效,导致管道二次泄漏[1-3],需采用焊前预热来防止冷裂纹的出现。然而,X80管道预热温度过高时会使管壁性能下降,焊后在接头残余应力作用下热影响区仍会发生裂纹[4]。因此,需要计算流动天然气环境下的管壁换热系数,以确定最佳的焊前预热温度。
求解流动天然气与管壁间的热交换系数,是获取管内外壁温度分布和确定焊接预热温度的基础。然而,热交换系数与多种参数有关,不同天然气成分含量下的热交换系数也有所不同[5]。因此,本文提出采用数值计算的方法来快速确定管道内壁热交换系数,并以忠武线天然气[6](甲烷97%,乙烷1.5%,氮气1%及丙烷0.5%)为例,来计算天然气在8MPa输送压力下不同气体流速、不同输送温度下的热交换系数[7,8],为天然气管道在役补焊的预热温度确定提供理论依据和基础数据。
1 计算过程
第一步,计算导热系数。首先通过拟合甲烷、乙烷、氮气及丙烷在低压下的导热系数曲线,计算出天然气在低压下的导热系数,然后计算单组分气体在高压下的导热系数,通过对比温度和对比压力来校正天然气在高压下的导热系数[9]。第二步,计算黏度。首先查询得到各组分气体在低压下的黏度[10],计算天然气的黏度且进行较正,通过对比温度和对比压力计算天然气在高压下的黏度。第三步,计算定压比热容。查询得知高压下各组分气体的定压比热容,计算出天然气在高压下某一温度的定压比热容。第四步,将前三步的结果代入公式,即可得到天然气的普朗特数。第五步,计算密度。查询得知各组分气体在高压下的密度,按照公式计算出天然气在高压下某一温度的密度。第六步,将第五步结果代入公式可计算出雷诺数。第七步,计算努塞尔数[11]。将普朗特数及雷诺数代入公式,可得知流动天然气[12]的努塞尔数。第八步,计算热交换系数。将第一步的导热系数与上一步的努塞尔数代入公式,可算出流动天然气与管壁的热交换系数[13]。基本计算过程如图1所示。

图1 计算过程流程图
1.1 导热系数计算
当压力较低时,混合气体导热系数的计算公式为:

式中,yi为混合气体中i组分的摩尔分数;Mi为混合气体中i组分的相对分子质量;λi为混合气体中i组分的导热系数。
可得出,低压下天然气在25℃和100℃时的导热系数分别为0.033754、0.04432,而高压下单组分气体的导热系数可先由公式计算得到,再通过气体的对比温度和对比压力,对高压下的气体导热系数进行校正[14]。
气体的对比温度可用式(2)计算得到,

Tc为气体的临界温度。
混合气体的临界温度可用式(3)进行计算得到,

Tci为混合气体中i组分的临界温度。
经计算,混合气体的临界温度Tc=192.5251k,再带入式(2)中,可得混合气体在25℃和100℃时的对比温度分别为1.5479和1.9374。
气体的对比压力可用式(4)计算得到,

Pc为气体的临界压力。
混合气体的临界压力可用式(5)进行计算,

Pci为混合气体中i组分的临界压力。
经计算,混合气体的临界压力Pc=4.5943,再带入式(4)中,得到混合气体的对比压力Pr=1.7413。则Pr=1.7413条件下对比温度与导热系数的拟合结果如图2所示。

图2 对比温度与系数比的关系
根据以上的拟合结果计算出天然气在25℃和100℃时的导热系数比分别为1.305591和1.163809,结合低压下天然气的导热系数,最终得到8MPa下天然气的导热系数,见表1。

表1 8MPa下天然气在各温度下的导热系数
1.2 黏度计算
首先,按照式(6)计算低压下天然气的黏度:

通过查询相关的数据库,分别得到甲烷、乙烷、丙烷、氮气四种气体在0.1MPa下不同温度的黏度,如表2所示。

表2 0.1MPa下气体的黏度
将表2中的数据带入式(6)得到0.1MPa下天然气的黏度如表3所示。

表3 0.1MPa下天然气的黏度
但由于天然气中含有非烃组分,会增加天然气的黏度值,要用式(7)进行校正,其校正值可用式(8)进行计算。
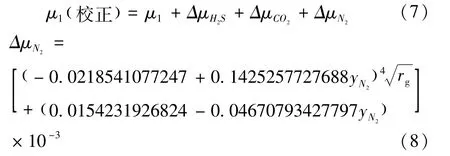
然后,校正后的结果如表4所示。

表4 黏度校正结果
若要求某一压力和温度下的黏度,可用式(9)进行计算:

当压力较高时,压力对天然气的黏度有很大影响。其黏度与压力为0.1MPa下的黏度之比有如下关系

式中:α(i,j)为系数;Pr为对比温度;Tr为对比压力。
通过计算得到天然气在25℃、100℃下的黏度比,再将计算结果带入式(9)即可得出天然气在8MPa、给定温度下的黏度,最终结果见表5。

表5 8MPa下天然气的黏度
1.3 定压比热容的计算
通过数据库可以得知气体在8MPa下的定压比热容,如表6所示。

表6 8MPa、给定温度下气体的定压比热容 (J/kg·K)
混合气体的定压比热容可由式(13)进行计算。

式中:Cp为气体混合物的定压比热容,J/(kg·K);cpi为组分 i的定压比热容,J/(kg·K)。
将表6中的数据代入式(13)得到天然气在8MPa、给定温度下的定压比热容,见表7。
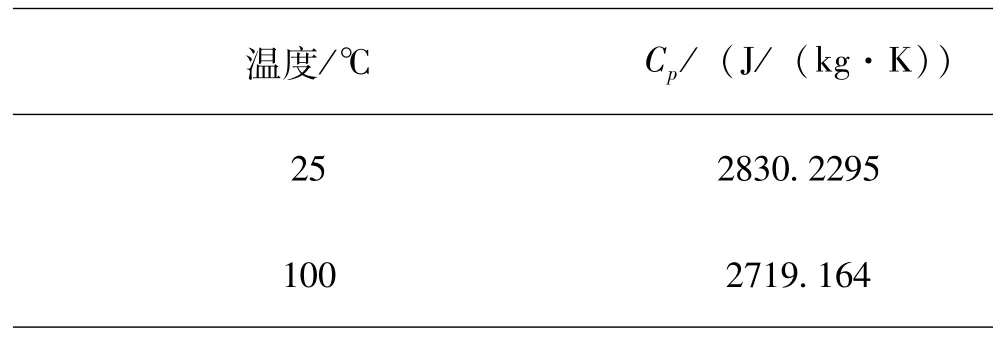
表7 天然气在8MPa、给定温度下的定压比热容
1.4 普朗特数的计算
气体的普朗特数可按式(14)计算,

式中:μ为纯气体或混合气体的动力黏度;Cp为纯气体或混合气体的定压比热容;λ为纯气体或混合气体的导热系数。
将表1、表5和表7中的结果带入式(14)得到天然气在8MPa压力下,25℃和100℃所对应的普朗特数,如表8所示。

表8 天然气在8MPa、给定温度下的普朗特数
1.5 密度的计算
混合气体的密度可按下式(15)进行计算。

通过查询数据库得到天然气各组分气体在8MPa、给定温度下的密度,如表9。

表9 天然气各组分气体在8MPa、给定温度下的密度 (kg/m3)
将表9中的数据带入式(15)得到天然气在8MPa、给定温度下的密度,见表10。

表10 天然气在8MPa、给定温度下的密度
1.6 雷诺数的计算
流体的流动状态分为层流、紊流和过渡流三种状态。流动状态和密度、流速、管径和液体的动力黏黏度可组成一个量纲为1的组合数Re,称为雷诺数[15],表达式如下:

天然气管道的设计流速一般为 10~15m/s[14],分别将10m/s、15m/s带入式(16),可以得出天然气在每个温度下状态下雷诺数的最小值和最大值。计算结果如表11所示。
1.7 努塞尔数的计算

将表8、表11中的计算结果带入式(17),得出流动天然气的努塞尔数如表12所示。

表12 流动状态下天然气的努塞尔数Nu
1.8 热交换系数的计算
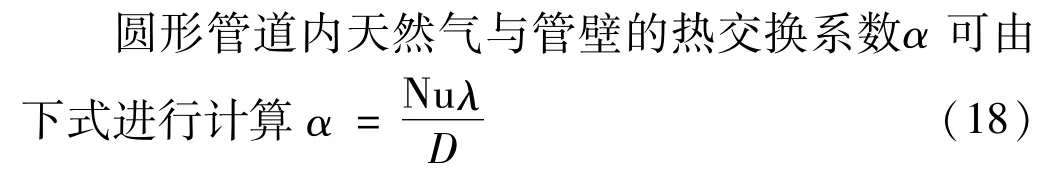
式中,D为管道内径。
将表1、表12中的结果带入式(18),得到流动天然气与管壁的热交换系数α见下表13。

表13 流动天然气与管壁的热交换系数α
2 结语
本文提出的天然气管道内壁热交换系数的数值计算方法可简便地计算任一工况条件下天然气管道内壁的热交换系数,能为天然气管道在役补强焊的预热温度确定提供理论依据和数据支撑。
