多元线性回归分析建立空气质量数据校准发布的数学模型
2020-11-02杨国颖
杨国颖
(兰州石化职业技术学院,甘肃 兰州 730060)
0 引言
空气污染对生态环境和人类健康危害巨大,虽然国家监测控制站点(国控点)对“两尘四气”有监测数据,且较为准确,但布控较少,数据发布时间滞后较长且花费较大,无法给出实时空气质量的监测和预报。某公司自主研发的微型空气质量检测仪花费小,可对某一地区空气质量进行实时网格化监控气象参数。在国控点近邻所布控的自建点,微型空气质量检测仪所采集的数据与该国控点同一时间的数据存在一定的差异,因此,需要利用国控点每小时的数据对国控点近邻的自建点数据进行校准[1-2]。
1 多元线性回归模型
多元线性回归模型的表达式为:
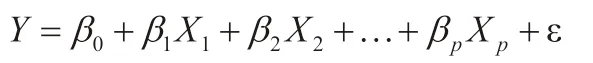
其中,β0,β1,…,βp的p+1个未知参数,称为回归系数。Y是因变量,而X0,X1,…,Xp是p个一般变量,即自变量。ε是随机误差,期望值为零时满足正态分布N(0,σ2)。
对空气质量数据校准这一实际问题,(Xi1,Xi2,…,Xip;yi),i=1,2,…,n,

如何利用国控点数据,对自建点数据进行校准,选用多元线性回归模型[3-5]。
国控点数据为PM2.5、PM10、CO、NO2、SO2、O3共6个监控数据,时间从2018/11/14 10:00至2019/6/11 15:00,每小时统计一次,共计4200条数据。自建点数据从2018/11/14 10:02 至2019/6/11 16:32,时间间隔5 分钟内统计一次,共234717条数据。对自建点数据进行处理,按照如10:00至10:59 分为一小时间隔,统计平均值。时间从2018/11/14 10:00至2019/6/11 16:00,共计4920条数据。
分整点统计数据,自建点4920条,国控点4200条,经初步比对,发现自建点和国控点均存在同一整点数据缺失情况,共有数据4983条,国控点缺失整点数据783条,自建点缺失数据63条。
进一步整理数据,剔除国控点缺失的783条和自建点缺失的63条数据,得到分整点统计有效数据4137条。
以国控点PM2.5为因变量,自建点11项数据为自变量建立多元线性回归模型[6-8]。
运用EXCEL数据分析工具箱,初步对国控点PM2.5进行回归分析。
1.1 对回归方程进行显著性检验
相关系数R=0.9530,回归方程是显著的,且具有95.3%的可信度。
1.2 对常数项和各线性项进行显著性检验
回归方程中的x5(SO2)、x6(O3)都是不显著的,剔除x5(SO2)、x6(O3),再次进行回归分析,发现x7(风速)p值为0.076456>0.05。
继续剔除x7(风速)做多元线性回归。从数据结果可以看出回归方程是显著的,且常数项和各线性项p值均<0.05,说明此时线性回归方程比较满意。
可认为去除的3个自变量的系数为0,由此得到,国控点PM2.5回归方程(除SO2、O3、风速):
y1=451.1230318+0.79243789x1+0.026076364x2+9.294 645509x3+0.078989972x4+0*x5+0*x6+0*x7-0.428006512x8-0.030787605x9-0.193950075x10-0.341499422x11
判定系数R-squared为0.9082,拟合程度非常好。
结论:国控点PM2.5 分整点预测值只需要自建点PM2.5、PM10、CO、NO2、压强、降水量、温度、湿度等8个数据,所获得的回归方程拟合度较好。
采用此方法可对国控点PM10、CO、NO2、SO2、O3其余5个指标逐一进行回归分析。
国控点PM10回归方程(除O3、风速):
y2=1287.600945+0.73533212x1+0.128642561x2+29.33321913x3+0.333424129x4+0.091232141x5+0*x6+0*x7-1.188444349x8-0.073684566x9-1.164787458x10-1.132177353x11
判定系数R-squared为0.6714,拟合程度较好。
国控点CO回归方程(除SO2):
y3=25.22694251+0.008571466x1-0.001009743x2+0.441 219094x3+0.002203022x4+0*x5+0.00075464x6-0.1319257x7-0.02410081x8+0.000381987x9-0.020357718x10-0.00319-9927x11
判定系数R-squared为0.5064,拟合程度较好。
国控点NO2回归方程(除CO、SO2):
y4=1331.278773+0.538119567x1-0.258976809x2+0*x3+0.411834389x4+0*x5-0.0951238x6-17.28883773x7-1.219421357x8-0.030514553x9-1.692427105x10-0.64718301x11
判定系数R-squared为0.5320,拟合程度较好。
国控点SO2回归方程(除温度、湿度):
y5=-373.850039-0.160919861x1+0.122208283x2+31.8 6182596x3+0.056660302x4-0.054798036x5+0.100801897x6-5.769067647x7+0.359102275x8+0.017623515x9+0*x10+0*x11
判定系数R-squared为0.4126,拟合程度较好。
国控点O3回归方程(除降水量):
y6=-755.359663+0.958786185x1-0.5708725x2-14.3186506x3-0.576558562x4+0.06212603x5+0.569078 55x6+15.74438408x7+0.77063655x8+0*x9+2.65918267 7x10-0.209917002x11
判定系数R-squared为0.8002,拟合程度较好。
由此可得到国控点PM2.5、PM10、CO、NO2、SO2、O3等6项数据与自建点PM2.5、PM10、CO、NO2、SO2、O3、风速、压强、降水量、温度、湿度等11项分整点数据的回归方程。
利用上述给出的6个回归方程,针对自建点测出的数据进行校准,即通过多元线性回归方程把自建点监测数据处理后对外发布[9-10]。
本文自建点11项数据是按照实时统计(间隔在5分钟内)分整点求得平均值,因此我们在研究分整点数据的基础上分析认为,空气质量数据的变化有一定的连续性,相邻数据的变化遵循一定的规律。我们将回归方程运用到自建点234717条数据中,得到自建点随时对外发布的校准数据。

表1 自建点11项分整点数据校准发布数据

表2 自建点11项分整点数据校准发布数据残差

表3 自建点11项随时监测数据234717条校准发布
2 模型分析
进一步对分整点数据校准发布和随时数据校准发布研究,发现一些数据小于0,呈负数出现。在实际监测中,这是不可能出现的,即构建的多元线性回归模型存在一定的误差,主要原因是虽然本文对国控点和自控点的数据进行了整理校对,但对存在的异常数据没有剔除,部分自建点的数据经分析针对国控点的数据高出2倍甚至更多,在初步构建模型时未删除,样本数据的有效性受到一定的影响,模拟精度降低。
针对以上数据分析,作11 元线性回归,建立y关于x1,x2,…,x11的回归模型如下:
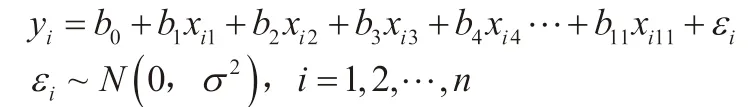
判定系数R-squared为0.908,拟合程度较好。
x5、x6的p值为0.68356、0.42959均大于0.05,即回归方程中的线性项x5、x6均是不显著的,x5最不显著,其次是x6。
3 多重共线性判断
xi多元线性回归共线性判断,回归模型的判定系数为,得到方差膨胀因子:

VIFi越大说明线性相关越显著,即存在共线性。通过计算,自建点VIF值分别为21.4928、26.6358、2.4873、1.6134、1.1576、2.2826、1.3750、7.1922、1.4545、10.0520、2.5397。由此可知,自变量x2中等程度共线性,x1、x2、x10共线性严重。
4 模型精度分析
运用MATLAB工具箱绘制预测校准数据的残差直方图和残差正态概率图,如图1所示。

图1 多元线性回归残差直方图和残差正态概率图
根据学生化残差寻找异常值,针对国控点PM2.5,自建点共出现195条异常数据,见表4。
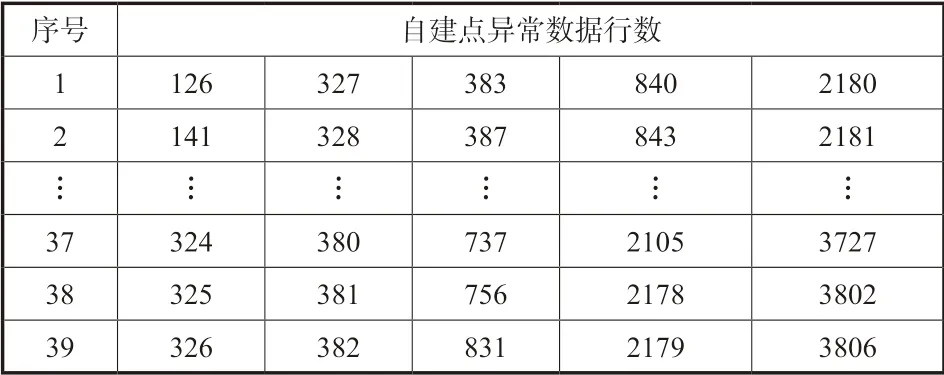
表4 自建点异常数据(国控PM2.5)
需要提高模型的精度和准度,剔除195项异常值,并将不显著项x5、x6去掉,重新建立多元线性回归模型[11-13]。
判定系数R-squared由0.908提高到0.942,拟合程度明显提高。
剔除异常数据后,x7风速的p=0.00044527<0.05,显著性检验为显著。
在前面建立的模型解析中,因没有剔除异常数据,导致x7在进一步的显著性检验中判定为不显著项,模型拟合的精度和准度发生偏差。
国控点其余5个自变量(PM10、CO、NO2、SO2、O3)的分析求解类同于国控点PM2.5的解法。

表5 国控点PM2.5与自建点PM2.5分整点对应值倍数表
5 结语
本文建立了多元线性回归分析模型,利用国控点的分整点数据,对自建点数据进行校准。模型虽然去除变量和剔除异常数据提高了精度,但由于自建点数据过于繁杂,在判断异常数据上对样本数据的分析还存在一定不足,比如国控点PM2.5与自建点PM2.5的值相比,高达10倍的数据也有出现。
对超出3倍以上的34条数据分析,仅有自建点第592条,自建点PM2.5是国控点PM2.5数值5倍左右的数据在回归模型中被判定为异常数据予以剔除。所以在超出高倍数情况下,建立的回归模型默认为是有效数据,这里有进一步讨论的空间和价值[14-16]。
