基于附加质量的桥梁结构损伤识别方法
2020-11-02段卫东周威高磊苏港刘伟合肥工业大学土木与水利工程学院安徽合肥230009
段卫东,周威,高磊,苏港,刘伟 (合肥工业大学土木与水利工程学院,安徽 合肥 230009)
1 引言
桥梁因老化损伤造成突然坍塌的事故屡见不鲜,仅1951-2000年间,美国共发生了617起桥梁倒塌事故。因此,对桥梁结构进行损伤识别成为当前土木工程领域的研究热点[1-3]。近年来,基于振动的桥梁结构动态损伤识别技术受到越来越多的关注,其基本想法是通过测试桥梁结构的动力响应,根据其振幅、固有频率[4]等动力参数的变化来诊断结构损伤。其中,基于频率改变的动态损伤识别方法,虽然有效地利用了频率测量精度高的优点,但存在可用的频率信息有限的问题。本文通过在桥梁原结构上不同位置分别附加质量已知的集中质量块,测量所得附加质量——桥梁系统频率,对其进行分析从而进行损伤定位。
2 损伤定位指标
对于多自由度体系,其自由振动的运动方程为:
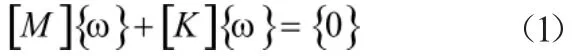
其特征方程为:

式中,[K]为多自由度体系的刚度矩阵;[M]为多自由度体系的质量矩阵;ω为多自由度体系的频率。
在80年代中期提出利用频率变化比的方法对结构进行损伤识别的是Cawley和Adams,他们通过结构的特征值及物理参数对灵敏度进行了分析,基于有限元原理提出了在结构中只存在单处损伤的情况下,损伤前后任意两阶频率的变化比只与损伤的位置函数有关,即可以通过损伤前后频率变化来定位损伤。将已知质量块放到桥梁的不同位置时(如图1所示),移动质量——桥梁系统的频率会发生变化,且此频率不同于桥梁的固有频率。将损前第i个梁单元的移动质量——桥梁系统频率记为fi,损后该单元系统频率记为fi',定义如下损伤定位指标:


图1 质量块移动示意图
3 数值验证
如图2所示简支梁,跨度L=3m,均分为15个平面梁单元,标号1、2、3.....15。弹性模量E=69GPa,泊松比为0.34,密度为2.72g/cm3,宽度d=0.1m,高度h=0.02m。图3两跨连续梁的参数与上述简支梁相同,并均匀分为30个单元。采用有限元模型,计算桥梁在无损和损伤及噪音影响条件下质量块分别置于各个单元时的频率,并计算其对应的损伤定位指标W。

图2 简支梁模型

图3 连续梁模型
3.1 单元刚度不均匀性的影响
对于真正的梁结构,由于结构和刚度的不同,其弯曲刚度的分布会随梁长而变化,而且随着时间推移,桥梁的刚度会出现不同程度的损伤,我们通过改变桥梁系统每个单元的刚度矩阵,在5%破坏范围内随机模拟桥梁系统的劳损情况,并作出模拟图。
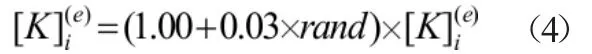
3.2 附加噪音的影响
在进行测试时,不可避免存在着环境噪音和测试设备噪音的影响,而噪音可能会对采集到的测试数据产生一定程度的“污染”,影响测试的准确性。本文通过添加噪音的程度对噪音大小进行描述,被噪音污染的信号,可按下式计算:
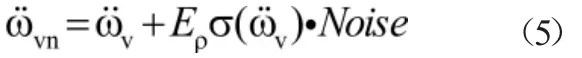

数值算例工况 表1
本节考虑的损伤工况如表1所示,对应的损伤定位结果见图4~图9,可见本文提出的损伤指标Wi能有效定位损伤位置。
3.3 数值模拟结果
①简支梁数值模拟结果
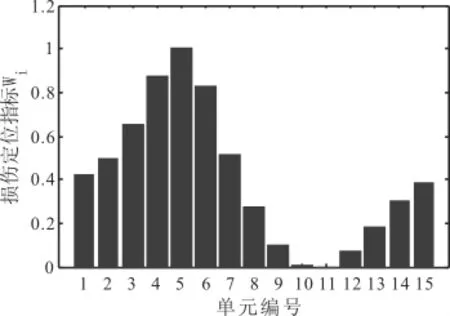
图4 工况一损伤定位结果
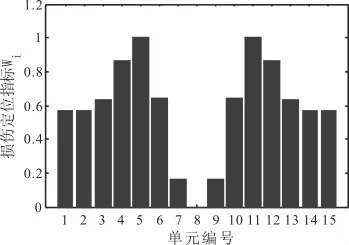
图5 工况二损伤定位结果
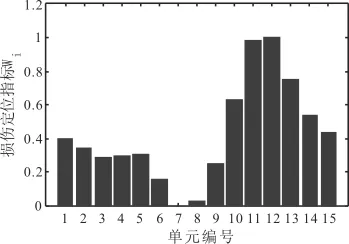
图6 工况三损伤定位结果
②连续梁数值模拟结果
见图7~图9。
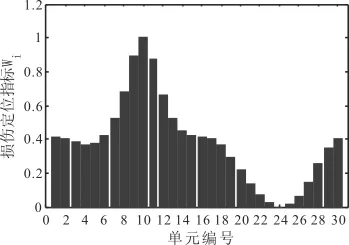
图7 工况四损伤定位结果
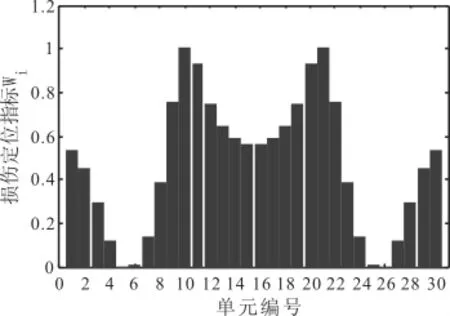
图8 工况五损伤定位结果

图9 工况六损伤定位结果
由上面的图形可以看出,当梁结构出现损伤时,其刚度矩阵会发生变化,对应单元的质量——桥梁系统频率也就会改变。在图形中相应的损伤单元会出现凸点,当桥梁结构损伤单元增多时,凸点更加明显,所以数值模拟中,损伤定位指标W可有效定位损伤。同时,通过对比我们也发现,噪音对于该方法损伤定位影响较小。
4 试验验证
4.1 试验材料及过程
本实验布置如图12和13所示,采用的铝合金梁的参数为:长3m,宽12cm,厚 2cm;密度:2.72g/cm3;弹性模量6.9e10;泊松比率 0.34;横梁的横截面积:0.02×0.1m3,实验用车轮子前后间距20cm,重0.85kg;将梁分为15个单元,每个单元为一个测点,在单元11处设置损伤。本次实验中,将无线传感器的发射装置用磁铁固定在小车上(如图10所示),接收装置与电脑相连,采用脉冲激励法中的敲击法,采用力锤在不同点激振,拾振器在固定位置拾振的方法,将载有不同载荷的小车模型分别放在15个单元格中进行测试(如图11所示)。

图10 传感器布置

图11 激励梁测试响应
4.2 试验结果
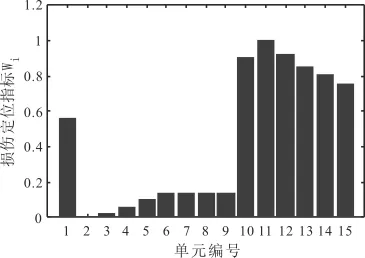
图12 试验损伤定位结果
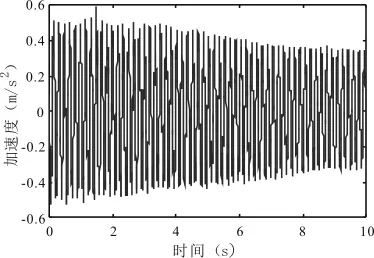
图13 加速度的时程图
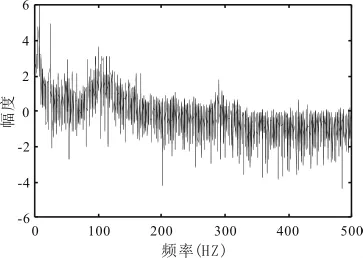
图14 频谱图
由上面图形可以看出,损伤定位指标在实际试验中存在;同时,试验结果与数值模拟结果拟合较好,说明在实际环境中损伤定位指标可有效定位损伤。
5 结论
本文定义了一基于移动质量—桥梁系统频率变化的损伤定位指标,并通过数值算例和试验室试验验证了该定位指标的有效性,该方法具有实施方便、精度高、效率高和结果直观的优点。通过对数值模拟图形与试验结果图形进行分析,现得出以下结论:
①当桥梁结构损伤时,其结构自身刚度将下降,从而导致其移动质量—桥梁系统频率逐渐降低,且随损伤程度的增加,移动质量—桥梁系统频率的下降速度也将加快。
②系统频率是一个整体性的参数,当结构的某一段单元发生损伤时,移动质量—桥梁系统频率的频率会发生变化,而且当质量块处于损伤单元时,系统频率值变化较其他位置更大,在损伤定位指标W图像中损伤位置有明显的凸点,可根据凸点位置识别损伤位置,且损伤单元越多,损伤位置越明显。
③试验环境下,所设定损伤定位指标有效,且附加噪音对定位损伤位置影响较小。
6 不足与展望
①在实际试验操作过程中存在的影响因素较多,本文对于有限元模型的修正不够细致,会存在误差。因此,下一步工作中需要对建立有效基准有限元模型的方法进行研究,并以此为基础进行桥梁结构损伤定位识别。
②本文所模拟的桥梁结构为简支梁和双跨连续梁,在实际应用中较为局限,需要进一步研究讨论相关结论对于拱桥等其他类型桥梁的适用情况并进行推广,使结论具有更加广泛的实际意义。
③下一步研究在建立有效的桥梁结构基准有限元模型基础上,讨论附加车辆的参数设计(轴重、轴距等)对修正效果的影响,以达到最佳修正效果。
