基于MMC拓扑优化方法的开洞深梁拉压杆模型研究
2020-11-02乔文正陈国荣
乔文正,陈国荣
(1.吕梁学院建筑系,山西 吕梁 033000;2.河海大学力学与材料学院,江苏 南京 211100)
1 引言
为了建立一种结构拓扑优化和CAD的直接联系,2014年大连理工大学郭旭教授提出了一种显式的结构拓扑优化方法,即基于可移动变形组件(moving morphable components,简称 MMC)拓扑优化方法[1]。该方法采用由具有显式几何参数的、能够在设计空间中自由移动并变形的组件作为描述结构拓扑的基本元素,通过这些组件的移动、膨胀、收缩、交叉和重叠来实现结构的拓扑的变化,其中组件的重叠和隐藏机制是实现拓扑变化的关键所在;2016年郭旭教授又进一步发展了与可移动可变形组件相对偶的、采用可变形孔洞作为设计基元的可变形孔洞法[2](moving morphable voids,简称MMV)。该方法采用B-样条函数来描述结构中的孔洞的边界形状,结构的优化的变量为孔洞的显式的几何参数。显式框架的拓扑描述方法一经提出,迅速得到了国内外学者的广泛关注。关于拓扑优化的研究进展,详见文献[3]。
拉压杆模型(strut-and-tie models,简称STM)将混凝土梁的力学行为简化为一个理想化的铰接桁架,提供了一个静力允许的荷载传递路径。STM特别适用于混凝土结构中D区域的设计。STM的理论基础最早可追溯到连续体结构的极限分析[4]。根据极限分析的下限理论,STM是一个仅满足构件和结点平衡和屈服条件的安全的下限解。
在实际工程中,深梁由于使用功能的原因,经常需要开洞。开洞深梁不仅是一类典型的D区域,还具有较复杂的应力分布。开洞深梁的拉压杆模型研究具有重要的理论和实际意义。关于开洞深梁的拉压杆模型的研究,学者采用了多种不同的方法,如荷载路径法[5,6]、基于性能的渐近结构优化方法[7,8]、固体各向同性材料惩罚方法[9]和基于试验的方法。文献[10]首次采用基于MMC的拓扑优化方法产生拉压杆模型,将显式的思想引入到拉压杆模型中,获得了成功。但对于开洞的复杂构件还未开展相应的研究。相比于传统的拓扑优化方法,MMC的优化方法克服了诸如锯齿的边界、网格依赖性和棋盘格现象等数值困难,而且设计变量数大为减少,提高了优化求解效率。
通过开洞深梁算例,采用基于MMC的拓扑优化方法产生可靠的STM。基于图像处理技术,提出一种自动的提取方法实现从拓扑优化结果到STM的自然过渡,尽可能地减少人为干预。
2 可移动变形拓扑优化方法
2.1 结构的拓扑描述函数
在MMC的拓扑优化中,结构的拓扑描述函数xs(x)可由下式表达:

和构件拓扑描述函数xi(x)为:

式中:Ωs和∂Ωs是 nc个组件所占的区域的内部和边界,Ωs为设计域D0的一个子域;Ωi和∂Ωi分别是第i个组件区域的内部和边界。
若采用直线型骨架厚度二次变化的组件形式(见图1),从而可得到xi(x)的具体表达式如下:
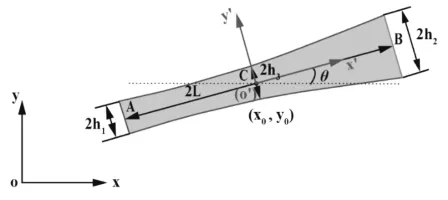
图1 直线骨架型组件简图
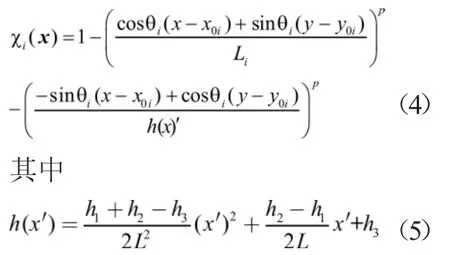
式中:x和y分别为整体坐标系中设计域内点的横和纵坐标;x'为局部坐标系中设计域内点的横坐标;x0i和y0i分别为整体坐标系中第i个组件的中心点横和纵坐标;Li和θi分别为第i个组件的半长轴和倾斜角(从x轴正方向逆时针旋转);p为超椭圆表达式中的参数,此处取6。
总之,在MMC的拓扑优化中,结构的拓扑可以用一个设计向量来唯一地确定,其中 di=(x0i,y0i,Li,h1,h2,h3,θi)T。
2.2 问题的列式
一般来说,用求解体积约束下柔度最小化的拓扑优化问题来间接地获得混凝土拉压杆模型。

式中:C和V分别是优化问题的柔度目标函数和体积约束函数;ε(·)表示线性应变张量,E表示组件的弹性张量。F和T分别表示组件的体力和Neumann边界上的面力;u和v分别是在域上的位移场和定义在域,且为允许域子域的相应的试函数;是Dirichlet边界上的给定的位移;V0和分别是设计域体积和给定的体积百分比上限;ud是设计变量d的容许集。E和μ分别是混凝土材料的弹性模量和泊松比。为了简化,此处取=0。
2.3 数值实现
2.3.1 有限单元分析
采用虚拟材料模型来实现结构的拓扑优化,材料的虚拟弹性模量为:
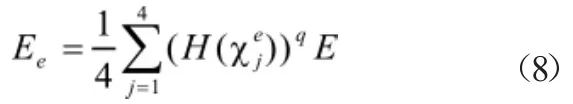
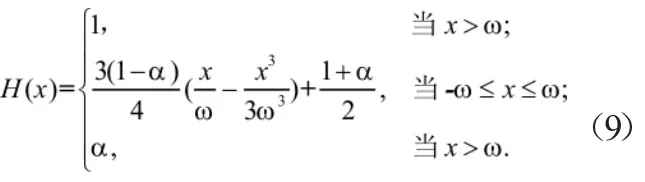
式中:ω是一个控制正则化大小的参数;α是一个较小的正数,其目的是确保整体刚度矩阵的非奇异性,通常取α=0.001。因此,式(6)中的目标函数、等式和不等式约束函数可进一步表示为:

2.3.2 设计灵敏度
基于梯度的最优化算法中,需求目标和约束函数对设计变量的导数,即为灵敏度分析。用a表示任意一个设计变量,则目标和约束函数的灵敏度分别为:

式中:ke和K分别为单元和整体刚度矩阵;ue为单元位移列向量;NE为有限单元总数。
3 从拓扑优化结果到拉压杆模型
3.1 概述
从拓扑优化结果到拉压杆模型的提取过程,最重要的是要保留他们之间的拓扑一致性。受到文献[11,12]的启发,采用一种自动的提取过程实现从拓扑优化结果到拉压杆模型的自然过渡。该方法的本质是一种基于像素的图像处理技术,该过程主要分两个阶段:细化阶段和提取阶段。图2为提取方法的流程。
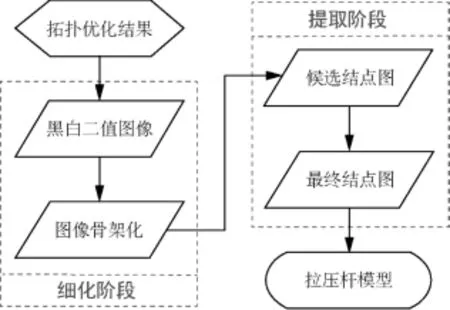
图2 提取方法流程
3.2 细化阶段
在细化阶段,拓扑优化结果的彩色图像首先被转换成灰度图,然后再转换黑白二值图像。运用图像处理的细化算法[13],可以从黑白二值图像中生成具有单像素宽度的骨架曲线。该细化算法的基本思想是迭代地删除位于边缘的像素,直到在不改变拓扑的前提下,没有多余的像素可以被删除,从而生成具有单像素宽度的骨架曲线。
3.3 提取阶段
在提取阶段,首先是检测可能的结点,形成候选结点(用蓝色方形点表示)图;其次去除多余的结点,形成最终结点(用绿色圆形点表示)图;最后确定各结点的连接关系,形成拉压杆模型图,从而完成提取阶段的工作。
4 数值算例
采用基于MMC的拓扑优化方法,首先对开洞深梁进行拓扑优化,从而获得最优的拓扑结构;其次实现从拓扑优化结果到STM的自动提取。
基于MMC的拓扑优化采用MATLAB拓扑优化代码[14],最小化算法采用著名的移动渐近线法[15]。图3为开洞深梁计算简图。
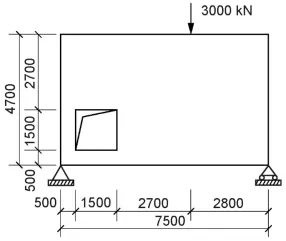
图3 开洞深梁
有限单元分析中,混凝土弹性模量采用30088 MPa,泊松比采用0.15,采用平面四边形等参单元,单元边长均为100 mm,单元总数为3300个。深梁厚度为100 mm,体积百分比上限取0.35。
图4为开洞深梁拓扑优化过程。在MMC的优化过程中,采用36个组件,设计变量数为252个。随着迭代次数的增加,这些组件通过移动、膨胀、收缩、相交和重叠来实现结构拓扑的变化,最终达到收敛要求。经过342次迭代,最小柔度目标函数值为45.59 kJ,最优拓扑见图4(d)。相比较于传统的隐式的拓扑优化方法,一方面克服了一些传统的数值问题,如网格的依赖性、锯齿的边界、灰度单元的存在和棋盘格现象等。另一方面,相比于传统的优化方法,设计变量数从3300减少到252个,与优化相关的求解效率会大幅提高。图5为目标和约束函数收敛过程曲线。
图6为拓扑优化结果的黑白二值图像和对应的骨架曲线,图7为候选结点图和由最终结点产生的拉压杆模型图。关于算法实现的细节详见文献[11]。图7中红色圆点表示的结点为荷载作用和简支支座的位置。需要指出的是,大部分的直接生成的拉压杆模型并不能直接使用,有时需要进行人为的微小改动来使得拉或压杆与边界平行或垂直,有时甚至需要添加适当的杆件形成几何不变体系。鉴于这种改动因人而异,此处并没有给出改动后的拉压杆模型图。
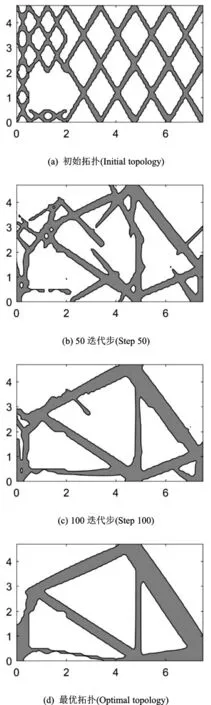
图4 开洞深梁拓扑优化过程
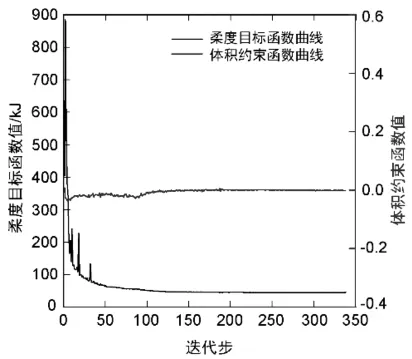
图5 收敛过程曲线
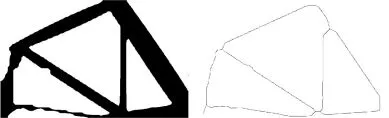
图6 最优拓扑的黑白二值图像和骨架曲线

图7 候选结点图和由最终结点产生的拉压杆模型图
5 结论
将MMC的拓扑优化方法与混凝土拉压杆模型相结合,重点研究了开洞深梁的拉压杆模型。借助图形处理技术,采用一种自动提取方法实现了从拓扑优化结果到STM的自然过渡。通过开洞深梁算例,得出以下结论:
①基于MMC的拓扑优化方法可以可靠且高效地产生开洞深梁的拉压杆模型;
②不但避免了灰度单元、网格依赖性和锯齿的边界等数值困难,而且优化求解效率更高;
③基于图像处理技术,实现了从拓扑优化结果到STM的自动化提取,尽可能减小了人为因素的影响。
