一种涡卷弹簧分离螺母装置设计及仿真分析

赫志亮,于 兵,宋保永,王 君

( 北京宇航系统工程研究所，北京 100076)

0 引言

连接分离装置的作用是连接航天器和运载火箭，并在某一时刻完成解锁动作，完成航天器与运载火箭的分离。分离装置既要保证航天器部段之间可靠连接，又要保证在分离信号下可靠分离，长期以来一直是航天领域技术的一项重要研究内容[1]。目前，载人航天任务中大量将火工分离装置[2]用于各舱段之间的连接与分离，存在诸多问题与局限性。首先，火工分离装置采用火工品作为动力源，由于火工品自身存在工作时爆炸冲击大、可测试性弱、安全性差等固有缺陷，无法满足新型载人飞行器以及未来载人航天任务对微冲击、可检可测及高可靠性的需求；同时，对于现有火工分离装置来说，大承载能力意味着解锁时需要的火工品药量也越大，从而带来更大的火工冲击[3]，无法同时满足大承载和微冲击的需求。

由于火工品自身存在不可检测、高冲击、高危险性、污染排放以及一次性使用等缺点，使得火工品驱动的分离装置同样存在着上述问题。为此，人们寻求采用非火工技术从根本上解决火工品存在的固有缺陷，从而实现分离装置的可检可测、微冲击、高安全性、无污染以及重复使用等功能，非火工锁紧释放装置的研制成为必然趋势[4]。

20世纪90年代初，国外就开始研究在分离装置上采用非火工驱动(Non-Explosively Actuated，NEA)技术，同时开展适应NEA技术的分离装置内部机构设计，完成了多种类型的非火工分离装置研制，并逐步应用于飞行试验。目前国外多采用NEA技术用于非火工分离装置的触发解锁，其中较为成熟的分离装置大致包括4类：热刀(熔断)触发类、形状记忆合金(SMA)触发类[5]、电机触发类[6]和电磁铁触发类。

本文基于金属带锁紧分离原理，提出了一种基于涡卷弹簧组件、由电磁铁触发的非火工点式分离螺母装置，将金属带锁紧分离的特性应用于非火工点式分离装置中，并研究了涡卷弹簧的张力、扭矩变化规律，探究装置的工作特性。

1 金属带锁紧分离装置原理

图1 RULSA示意图Fig.1 Schematic diagram of RULSA

由法国STOEREM公司研制的Resettable Ultra Low Shock Actuator(RULSA)[7]装置采用了金属带锁紧分离的原理。装置采用电磁铁作为触发元件，如图1所示。此种装置采用分瓣夹紧螺母和螺栓实现连接和分离，在分瓣夹紧螺母外面缠绕金属带使夹紧螺母夹紧。金属带层与层之间存在摩擦力，能够将内部的载荷经过金属带摩擦力层层耗散，所以在金属带最外侧只需要一个较小的力就能实现最内部螺栓在大载荷工况下的锁紧。同样，也只需要一个较小的解锁力便可以使机构解锁，完成夹紧螺母的释放。同时，在释放过程中，由于金属带的缓慢释放作用，装置产生的冲击也非常小。

2 装置设计

为了满足未来载人航天任务中对复杂舱段间可靠连接以及微冲击、高可靠的分离需求，本文提出了一种基于此原理的涡卷弹簧分离螺母装置结构，设计了一种大承载、非火工、微冲击、高可靠、模块化的涡卷弹簧分离装置，并研究了涡卷弹簧及整个分离装置的工作特性。

2.1 结构组成及原理

涡卷弹簧分离装置整体结构如图2所示。锁定触发单元为旋转电磁铁触发结构，包括两个旋转电磁铁以及制动阀。解锁传动单元包括释放压簧、释放销、旋转盘以及涡卷弹簧缓释结构。分离执行单元为分瓣螺母、螺栓结构。

图2 涡卷弹簧分离螺母装置示意图Fig.2 Schematic diagram of separation nut based on vortex coil spring

装置采用了涡卷弹簧的锁紧分离原理，加载状态时，涡卷弹簧抱紧分瓣螺母，螺栓与分瓣螺母按正常的螺纹副进行连接，此时螺栓即可承受外部载荷。涡卷弹簧的内圈固定在分瓣螺母上，外圈固定在旋转盘上，可通过转动旋转盘来实现抱紧或释放分瓣螺母的功能。加载状态时，与旋转电磁铁连接的挡柱限制释放销，释放过程中，旋转电磁铁转动，释放销在释放压簧的作用下向上移动，即可解除释放销对旋转盘的周向限制，涡卷弹簧外圈随着旋转盘在涡卷弹簧的作用下旋转，使得分瓣螺母随着径向移动，螺栓从分瓣螺母中脱出，完成释放。此装置采用旋转电磁铁进行驱动，能够反复使用，所以在正式使用前可以进行多次解锁测试，检查产品的工作性能。

装置的各个模块均采用冗余设计。设计了冗余的释放压簧，一旦触发解锁，任一释放压簧均可完成释放销的作动。同样，装置设置了两个释放销，用于加强对旋转盘的锁定。对于分瓣螺母的释放，在各个分瓣螺母之间设置了分离弹簧，对分瓣螺母进行冗余解锁。

2.2 涡卷弹簧组件特性分析

2.2.1 张力分析

对于承载力转化机构，本文通过涡卷弹簧机构实现。涡卷弹簧在满足自锁条件后，只需满足强度便可以可靠地锁紧分瓣螺母，当涡卷弹簧抱紧分瓣螺母时，将其看作一个整体圆筒[8]，由拉美公式可得涡卷弹簧内圈径向应力p1与缠绕圈数之间的关系[9-10]，如式(1)所示

(1)

式中，σsd为涡卷弹簧钢的许用强度，p1为涡卷弹簧缠绕锁紧应力，A为涡卷弹簧内圈面积，r0为涡卷弹簧内圈半径，t为涡卷弹簧厚度，FN2为分瓣螺母与涡卷弹簧的接触力，λ为安全系数。

选择涡卷弹簧材料为12Cr17Ni7，将其主要参数代入式(1)，当螺栓连接时，涡卷弹簧的厚度为0.3 mm，涡卷弹簧圈数m为20圈。

由于涡卷弹簧受径向力作用会发生弹性变形，每一层应力随圈数的增加成递减趋势。将外部径向压力变化增量与缠绕层径向力增量用Δp1[11]表示。则根据拉美公式，Δp1表达式为

(2)

式中，pn,n-1为第n圈对第n-1圈的径向压力，E1为涡卷弹簧弹性模量，E2为分瓣螺母弹性模量，R为分瓣螺母内孔半径，r0为涡卷弹簧内圈半径，ε1为涡卷弹簧泊松比，ε2为分瓣螺母泊松比。

经过整理，可以得到

σ=

(3)

其中

式中，f为涡卷弹簧每层间的摩擦系数，φ为涡卷弹簧缠绕包角，σ为钢带截面单位张力，t为涡卷弹簧厚度，b为涡卷弹簧宽度。

分瓣螺母选择材料30CrMnSiNi2A，查得材料相关参数后代入式(3)，可得到钢带截面单位张力σ与所用钢带层数的关系曲线，如图3所示。

图3 张力与层数关系Fig.3 Relation Between stress and layer of vortex coil spring

从图3中发现，随着涡卷弹簧层数增加，涡卷弹簧内部的张力约成指数型减小趋势，并且当涡卷弹簧的圈数大于7时，涡卷弹簧的最大张力小于其许用应力σsd(图中红线所示)，而方案中所选用的涡卷弹簧的圈数为20圈，其最大应力为424 MPa，安全系数为2.1。

2.2.2 扭矩分析

由于该装置用到的涡卷弹簧直接驱动旋转盘转动，进而使得分瓣螺母径向移动完成解锁，其扭矩随旋转盘转角的变化规律将直接影响装置解锁性能。

涡卷弹簧的工作状态是一端固定，另一端作用扭矩后，材料受弯曲力矩产生弯曲弹性变形从而使弹簧在自身平面内产生扭转，其变形角的大小和扭矩成正比。平面涡卷弹簧有非接触型平面涡卷弹簧和接触型平面涡卷弹簧两种类型[12]。非接触型平面涡卷弹簧在工作中各个弹簧圈均不发生接触，特性曲线为直线型；而接触型平面涡卷弹簧在工作时相邻弹簧圈之间互相接触，圈数较多，两种类型弹簧特性曲线如图4所示。

(a)非接触型

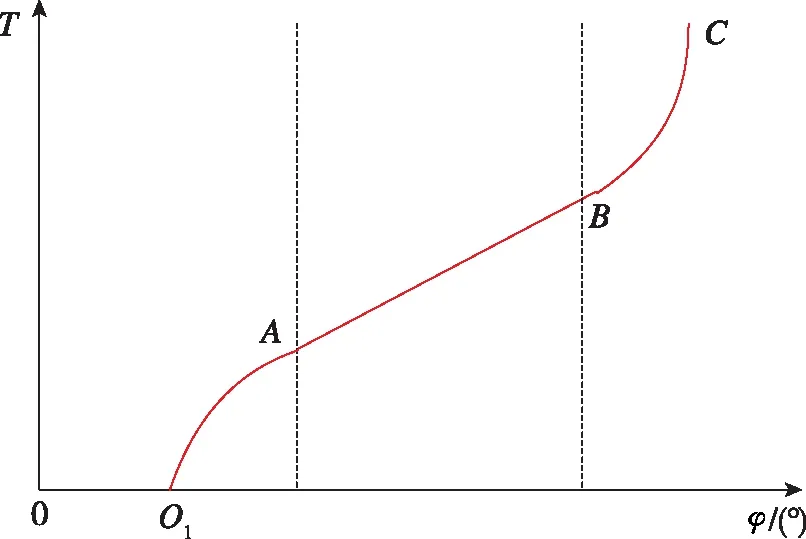
(b)接触型图4 涡卷弹簧理论特性示意图Fig.4 Theoretical characteristics of vortex coil spring

该涡卷弹簧内圈挂钩卡住分瓣螺母完成固定，外圈卡在旋转盘上。锁紧状态时，扭矩作用于旋转盘上。由于旋转盘对涡卷弹簧的外圈限制，涡卷弹簧相当于被限制在簧盒中，整个涡卷弹簧缠绕方式为接触型。

涡卷弹簧被放入旋转盘后，大部分弹簧圈紧压在旋转盘的内壁中，当涡卷弹簧卷紧时，弹簧圈逐渐离开内壁，此时的特性曲线为曲线，如图4中O1A段所示。在AB段时，涡簧在全长内工作，所以特性曲线为线性；BC段表示继续加载时，涡簧各圈逐渐卷紧从而导致其特性曲线急剧变化为渐增型，但是由于弹簧圈卷全部缠绕在分瓣螺母之前，其实际工作圈数小于总转数，其特性曲线已不满足平时所用扭矩规律，可以认为在C点时弹簧已经完全卷紧，从而可抱紧分瓣螺母。

为得到涡卷弹簧准确的特性曲线，采取直接测量的方法，将涡卷弹簧置于旋转盘中，采用正向测量与回程测量方法对比在锁紧过程与解锁过程中涡卷弹簧扭矩特性规律。将多次测量结果进行整理得到如图5所示特性曲线。

图5 涡卷弹簧测量特性曲线Fig.5 Measured characteristic curve of vortex coil spring

图中坐标原点取旋转盘最后静止位置，即图4中O1点位置。从图5可以看出，在锁紧过程中涡卷弹簧扭矩变形角特性曲线与图4接触型特性曲线基本一致，包括涡卷弹簧离开旋转盘阶段，线性增长阶段，突然增长阶段；而在释放过程中涡卷弹簧特性曲线出现了较为明显的回程误差，大致也经历3个阶段：扭矩的急剧下降阶段，扭矩线性平稳阶段，以及最后的平稳下降阶段。

分析其产生较大回程误差的原因，认为是涡卷弹簧卷紧时产生自锁现象，导致释放过程中开始受到自锁作用，在扭矩大幅减小的情况下转角只是有很小的降低，而当扭矩下降到某一刻时，伴随着转角到达某一值，涡卷弹簧间产生间隙，进而使得涡卷弹簧间无法再产生自锁，涡卷弹簧迅速回转即转角突然减小，最后扭矩随转角下降为零。

在释放过程中，涡卷弹簧扭矩的锁紧特性曲线对于解锁性能几乎没有影响，而回程特性曲线将直接影响解锁性能，因此对涡卷弹簧回程特性的准确描述尤为重要。为获得涡卷弹簧回程特性准确描述，采用直接拟合数值方法进行计算分析。

用分段函数近似拟合回程特性曲线

(4)

用最小二乘法计算得到相关参数，获得拟合曲线如图6所示。从图6可以看到，该拟合曲线可较为准确地描述涡卷弹簧回程特性曲线，可用该拟合曲线近似替代涡卷弹簧回程特性曲线。

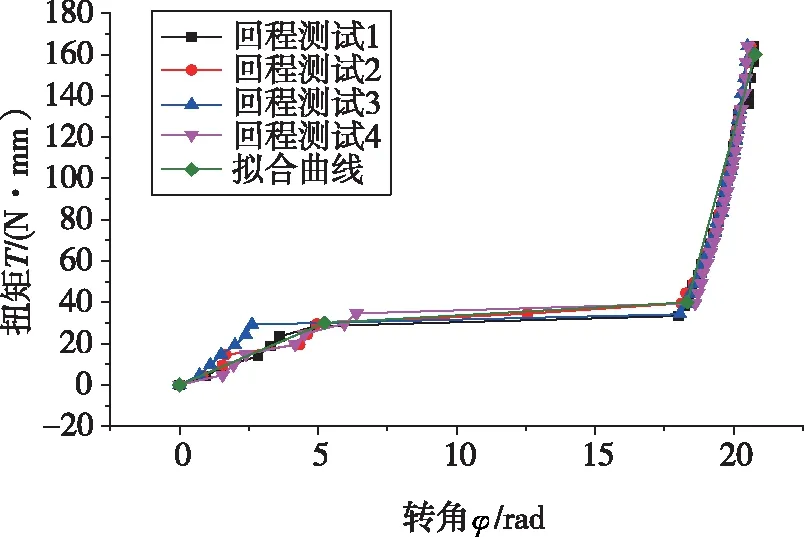
图6 涡卷弹簧回程特性曲线Fig.6 Return characteristic curve of vortex coil spring

3 仿真分析

由于实际的释放机构较为复杂，为简化分析，将其模型进行了简化。简化内容如下：1)所有连接螺钉、螺母及旋转电磁铁去除；2)用驱动力矩代替旋转电磁铁直接作用于制动阀上；3)复杂零部件的倒角去除；4)两个压缩弹簧去除，从Adams中直接设置弹簧力作用于销子柄与轴套上；5)为简化分析，将螺栓和分瓣螺母上的螺纹简化为旋转切除形式，其齿形、齿间距与实际的螺纹螺距相同，对仿真分析的结果影响较小；6)用螺钉连接多个零件，转化为一个零件进行仿真；7)涡卷弹簧用3个螺母挡块来代替，螺母挡块可径向移动，代替涡卷弹簧的锁紧与释放，由于分瓣螺母径向移动约1.5 mm，螺栓即可从分瓣螺母中脱离出来，涡卷弹簧转动17.4 rad即可将涡卷弹簧全部缠绕在分瓣螺母上，所以在Adams仿真分析时，转盘转动17.4 rad螺母挡块径向移动1.5 mm，期间螺栓即可从分瓣螺母中脱离出来，完成释放。

在简化仿真模型中，挡柱可沿轴向转动，当需要释放时，对挡柱施加力矩使挡柱转动；在加锁时，释放销受到垂直向上的弹簧力，在加锁时，释放销是插入旋转盘的限位孔中的，并在旋转盘转轴上施加一个与其转角有关的力矩，其变化规律与2.2.2节中测得的扭矩与转角的关系曲线相同，如式(5)所示

T=

(5)

在0～20 ms之间为加锁状态，螺栓加载500 N；20 ms后对挡柱施加50 N·mm的释放力矩，为释放开始时间；当挡柱转过约30°，释放销在压缩弹簧的作用下向上升，过程中可解除释放销对旋转盘的周向限制，旋转盘转动的过程中，螺母挡块径向移动，直到螺栓从分瓣螺母中脱出。

底板与分瓣螺母、分离盘与分瓣螺母之间的摩擦系数设置为0.2，螺纹连接处的摩擦系数设置为0.2，销子与轴套之间摩擦系数为0.3，制动阀与释放销之间的摩擦系数为0.4，释放销与旋转盘摩擦系数取0.4，其余摩擦力不考虑[13]。

采用Adams进行装置工作过程的仿真分析，根据仿真结果，在仿真时间为20 ms时对制动阀施加扭矩，此为释放开始时刻，随后制动阀转动，当制动阀转动到30°时，释放销开始向上移动。制动阀转动30°所用时间约为5 ms，释放销向上移动的时间约为4 ms，与理论计算接近。

当释放销向上移动一定距离后，旋转盘就不再受其限制，而在所施加的扭矩(模拟涡卷弹簧)的作用下转动。当释放销向上移动3 mm，外转盘就不再受其限制，并开始转动。

图7 分瓣螺母和螺栓运动过程Fig.7 Displacement of separation nut and bolt

当旋转盘开始转动后，施加在旋转盘上的力矩作用下转动17.4 rad，时间为84 ms，如图7所示。旋转盘从0 rad转动到17.4 rad期间，分瓣螺母会随着螺母挡块一起径向比例移动1.5 mm，期间即可将螺栓释放。分瓣螺母逐渐产生径向位移过程中，螺栓首先会缓慢移动，当分瓣螺母径向位移一段距离时，螺栓上的螺母齿才完全从分瓣螺母齿中脱出，随后螺栓才快速从释放机构中脱出。当分瓣螺母移动约1 mm时，在实际工作过程中，螺栓与释放机构的预紧力全部消失，达到了缓慢释放并降低冲击的目的。分瓣螺母位移为1.5 mm的时间为84 ms，则开始加力矩到螺栓脱出的时间为64 ms，与所计算的释放时间接近。

4 结论

针对航天器连接与分离的要求，以及目前广泛使用的火工分离装置的缺陷，本文提出一种新的涡卷弹簧非火工分离螺母装置，并对装置进行结构设计，对主要部分进行力学特性分析。本文通过对装置的关键部分为涡卷弹簧组件进行分析，分别研究其在装置承载和解锁过程中的特性。同时，对装置的工作过程进行仿真分析，获得装置在解锁过程中主要零部件的运动特性。

后续工作将考虑进行涡卷弹簧分离螺母装置的承载和解锁试验，通过测量试验中的相关数据，研究涡卷弹簧分离螺母装置的实际工作性能，并验证涡卷弹簧的不同参数选择对于装置性能的影响。