求解单位L∞范数下带值约束的最短路逆问题的算法∗

于成成 周泽聿 张斌武

（1.河海大学企业管理学院 常州 213022）（2.河海大学常州校区数理教学部 常州 213022）

1 引言

最短路问题是一类很重要的问题，其逆问题也具有很大的研究价值，它们在交通网络、通信网络等实际问题中有着广泛的应用。同时很多网络问题的逆问题也可能转化成最短路逆问题，最短路逆问题的解决有助于许多其他网络问题的解决。

近年来，最短路逆问题受到众多学者的关注，相关学者在最短路逆问题上也取得了一些进展。D.Burton 和Ph.LTiont［1］首先提出最短路逆问题，并使用二次规划的算法来求解L2范数下的最短路逆问题。Zhang Jianzhong等［2］引入列生成算法来求解单位L1范数下的最短路逆问题。Ahuja等［3］将单位L1范数下的最短路逆问题转化为最短路问题，从而得到了一个强多项式时间算法；将单位L∞范数下的最短路逆问题转化为最小平均圈问题；将非单位L∞范数下的最短路逆问题转化为最小费用和时间比例图问题。Xu Shaoji 等［4］将非单位权重下的最短路逆问题转化为最小费用流问题。在有值约束的条件下，Burton等［5］证明了非单位L2范数下带值约束的最短路逆问题是NP完全问题。张斌武等［6～11］研究Hamming 距离下各种网络的最短路逆问题及改进问题，对一些特殊网络给出了强多项式时间算法及近似算法，并证明了Hamming距离下一般网络的最短路逆问题是NP 困难的。除此之外，还有学者［12～14］研究了其他约束条件下的最短路逆问题，取得了一些进展。

本文研究单位L∞范数下带值约束的最短路逆问题，要求调整边长度向量，使得给定路径P0为新长度向量下图G的最短路径，且在新长度向量下P0的长度不超过给定的上界，并使得边长度的最大改变量最小。

最短路逆问题在实际生活中有着重要的应用。例如，有一个交通网络G=(V，E，w)，V集合表示不同的城市，E集合表示城市之间的道路，w集合表示车辆通过不同道路的时间向量。现在有两个重要的城市s和t，两城市间存在若干的道路，其中包含一条从s到t的城际快速通道P0，要求车辆通过城际快速通道所用的时间为两城市所有道路中最短的，同时车辆通过城际快速通道所用的时间不能超过给定的上界K。为了使城际快速通道P0成为连接两城市s和t最快的道路，需要对许多道路进行改造，改造会产生一定的费用，在满足要求的情况下，总的调整费用最小。

2 问题介绍

L∞范数下带值约束的最短路逆问题可以描述为

要求改变边长度向量w，使改变之后的长度向量={，...，} 满足：

1）P0为图=(V，E，wˉ )上的最短路；

2）(P0)≤K；

3）‖w-‖∞=max(ci|-wi|;ei∈E)最小。

本文主要研究边单位改变费用相同的情况，即ci=1，i=1，2，...，m。

3 单位L∞范数下带值约束的最短路逆问题的算法

为给出所研究问题的算法，先对图G的边长度向量w进行如下调整：若ej∈P0，则将其边长度调整为负值，即=-wj；若ej∉P0，则其边长度不进行调整，即=wj。调整之后的图记为G′=(V，E，w′)。

定义1在w′下，若圈C上所有边的长度之和小于零，即＜0，则称圈C为负圈。

引理1［3］路径P0为图G上的最短路的充分必要条件是图G′中不存在负圈。

由引理1 可知，若要使得P0成为图G上的最短路径，只需要调整图G′的边长度向量w′使其不存在负圈。

定 义2设Ω 为 图G′中 圈 的 集 合，对∀C∈Ω，定义平均圈为圈C上边的长度和与边个数的比值，记为其中 |C|为圈C上边的个数。最小平均圈λ*表示集合Ω 中所有圈其平均圈的最小值，即λ*=。

引理2［3］若图G′的最小平均圈λ*＜0，则是使图G′不存在负圈的最小调整量。

推论1在图G中，使得P0成为最短路的最小调整费用为|。

下面对图G′分两种情况进行讨论：

1）当图G′不存在负圈时，由引理1可知，P0已经为图G的最短路径；

故单位L∞范数下最短路逆问题即转化为求图G′的最小平均圈问题。

下面给出求G′的最小平均圈的方法：对无向图G′进行如下调整：若ej∈P0，则将ej调整为单向边，且边的方向与路径P0的方向相同；若ej∉P0，则将ej调整为双向边。调整之后的有向图记为图G″，其最小平均圈记为λ*0。Karp［15］给出了如下的求解有向图G″中强连通分量的最小平均圈的算法，其算法的时间复杂度为O(nm)。

其中Fk(v)表示从起点s到点v必须强制经过k条边的最短路径。Fk( )v计算公式为

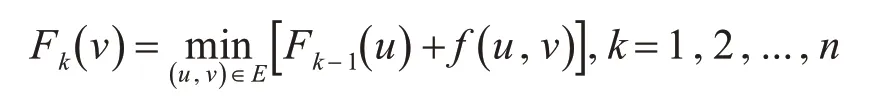
其中f(u，v)表示图G″中点u到v的边长度。且有F0(s)=0；F0(v)=∞，v≠s。

容易证明图G′的最小平均圈等于图G″的最小平均圈，即λ*=，故λ*可在时间复杂度O(nm)内求出。

下面给出求解单位L∞范数下带值约束的最短路逆问题的算法。

该算法的思想是：将图G调整为含负权图G′，求解图G′的最小平均圈λ*，设单位L∞范数下满足最短路逆问题约束的最小调整费用为μ1，若λ*》≥0，根据引理1，P0已为图G的最短路径，则μ1=0；若λ*＜0，根据引理1和引理2，使得P0为图G最短路径的最小调整费用为 |λ*|，则μ1=-λ*。计算t=(dw(P0)-K)/ |P0|，设单位L∞范数下满足值约束的最小调整费用为μ2，若t≤0，的长度已不超过上界K，则μ2=0；若t＞0，满足值约束的最小调整费用为t，则μ2=t。设单位L∞范数下带值约束的最短路逆问题的最小调整费用为μ*，则μ*为 调 整 费 用μ1，μ2的 最 大 值 ，即μ*=max(μ1，μ2)。算法的具体过程如下：

算法1（求解单位L∞范数下带值约束的最短路逆问题的算法）：

系统设置有完备的日志管理功能，网站管理员登录站群后台后的每一步操作，都有详细的记录。如谁，在什么时间，用什么IP，发布了什么内容，上传了什么图片、附件、视频等。对操作记录的完备管理，是实现站群系统安全管理的重要辅助。

Step1：将图G 转化为图G′，求解图G′的最小平均圈λ*。若λ*》≥0，则μ1=0；若λ*＜0，则μ1=-λ*。

定理1μ*=max(μ1，μ2)为单位L∞范数下带值约束的最短路逆问题的最小调整费用。

证明下面对μ1，μ2的取值分四种情况：

1）μ1=0，μ2=0

显然图G的路径P0是最短路，且满足dw(P0)≤K，其权重向量w不需要进行调整，因此μ*=max(μ1，μ2)=0 为单位L∞范数下带值约束的最短路逆问题的最小调整费用。

2）μ1＞0，μ2=0

图G的路径P0不是最短路，但满足dw(P0)≤K，由引理1 和引理2 可知，μ1= |λ*|为满足最短路约束的最小调整费用，因此μ*=max(μ1，μ2)=μ1为单位L∞范数下带值约束的最短路逆问题的最小调整费用。

3）μ1=0，μ2＞0

图G的路径P0是最短路，但不满足dw(P0)≤K，μ2=t为满足值约束的最小调整费用，因此μ*=max(μ1，μ2)=μ2为单位L∞范数下带值约束的最短路逆问题的最小调整费用。

4）μ1＞0，μ2＞0

此时图G的路径P0不是最短路，且不满足dw(P0)≤K。

μ*=max(μ1，μ2)≥μ1= |λ*|，由引理2 可知，|λ*|是使图G′不存在负圈的最小调整量，故μ*的调整量可以使得图G′不存在负圈，即满足最短路的约束；μ*=max( )μ1，μ2≥μ2=t，t是单位L∞范数下满足值约束的最小调整量，故μ*的调整量可以使得满足值约束。

因此μ*=max(μ1，μ2)的调整量可以同时满足最短路约束和值约束。

设μa满 足 0 ≤μa＜μ*。 若μ1≥μ2，有μa＜μ1= |λ*|，由引理2 可知，|λ*|是使图G′不存在负圈的最小调整量，故μa的调整量不可以使得图G′不存在负圈，即不满足最短路约束；若μ1＜μ2，有μa＜μ2=t，t是单位L∞范数下满足值约束的最小调整量，故μa的调整量不满足值约束。

因此小于μ*的调整量不可以同时满足最短路约束和值约束。

综上，μ*的调整量可以同时满足最短路约束和值约束，且小于μ*的调整量不可以同时满足最短路约束和值约束。因此μ*=max(μ1，μ2) 是单位L∞范数下带值约束的最小调整费用。

综合以上四种情况，定理1得证。

记图G调整之后的长度向量为w*=，由定理1 可知，得到的长度向量wˉ即为单位L∞范数下带值约束的最短路逆问题的最优解。算法1的时间复杂度为O(nm) 。

4 计算实例

下面给出一个实例，设图G=(V，E，w)，如图1所示。给定路径P0为A→B→C→E→F，其中A为P0的起点，F为P0的终点，其边长度向量w见图1，最短路径的长度的上界为10。现求解图G在单位L∞范数下带值约束的最短路逆问题的最优调整量。

将图G调整为负权图G′，如图2所示。

为求图G′的最小平均圈λ*，将其调整为有向图G″，如图3所示。

根据Karp 的算法求解图G″的最小平均圈计算得=-1.40。故单位L∞范数下满足最短路逆问题约束的最小调整费用为μ1=1.40。

计算得t=(dw(P0)-K)/ |P0|=1，故单位L∞范数下满足值约束的最小调整费用μ2=1。因此最优 调 整 量μ*=max(μ1，μ2)=1.40 ，调 整 之 后 的 图=(V，E，wˉ )如图4所示。

为了验证结果的正确性，借助二分法进行验证：经过λ1=1 的调整，图G不同时满足最短路和值约束的条件，经过λ2=2 的调整，图G同时满足最短路和值约束的条件，依据二分法的思想再判断经过λ3=1.5 的调整后图G是否满足条件，依次迭代。图G的调整量经过9 次迭代之后误差＜0.001，二分法计算的最优调整量为1.3998，在误差允许范围内与本文提出的算法相等，证明了算法的正确性。

5 结语

本文研究了单位L∞范数下带值约束的最短路逆问题，将单位L∞范数下的最短路逆问题转化为含负权图G′的最小平均圈问题。给出单位L∞范数下带值约束的最短路逆问题的算法，该算法并不需要求出所有的圈，算法的时间复杂度为O(nm)，并证明算法得到问题的最优解。给出了一个计算实例，用二分法验证算法的正确性。该研究方法对某些最短路逆问题的求解有一定的借鉴意义。

还有许多带值约束的最短路逆问题值得研究。如单位L∞范数下边的长度有界带值约束的最短路逆问题、L∞范数下的带值约束的最短路逆问题、L1范数下带值约束的最短路逆问题等。