Finite-time control of formation system for multiple fligh vehicles subject to actuator saturation

ZHAO Enjiao,ZHONG Zenan,and ZHENG Xin

1.School of Automation,Harbin Engineering University,Harbin 150001,China;2.Shanghai Academy of Space flight Technology,Shanghai 200233,China

Abstract:This paper investigates the problem of formation tracking control for multiple fligh vehicle(MFV)system considering actuator saturation constraints.First,the formation tracking control model is established.Then,the problem of formation control of the MFV system is converted to the convergence of a dynamical system,which is obtained by using the differential geometry theory.A class of saturation functions is introduced,and on this basis a second-order finite-tim formation control protocol is developed.With the help of the homogeneous theory and Lasalle’s invariance principle,it is theoretically proved that the designed formation protocol could complete the formation task in finittime,and the control inputs are shown to remain within their available actuating limits.Finally,simulations are performed to verify the effectiveness of the scheme.

Keywords:formation control,multiple fligh vehicle(MFV),finite time,actuator saturation.

1.Introduction

In recent years,the area of cooperative control has become an important research field motivated by the requirement to study engineering issues with new and efficient methods.In contrast to the traditional control ways,cooperative control is always distributed and does not depend on the unique central control unit only.Therefore,the cooperative control systems have the benefits of being robust,efficient,and flexible,allowing the control systems to have better performance in the new control strategies.

With the quick development of the aerospace technology,the conventional combat strategy using a single flight vehicle cannot satisfy the demands of the combat mission in complicated combat fields.In order to improve the hitting accuracy and enlarge the defense area,the cooperative combat system using multiple flight vehicles(MFVs)has been a research focus in recent years.The cooperative combat system can be applied in a variety of fields,including cooperative path planning[1],formation control[2],cooperative guidance[3],multiple sensor and data fusion[4],etc.Formation control is the key technology in cooperative attack,which plays an important role in the cooperative combat.

There are several methods for formation control design in general,such as virtual leader,leader-follower and behavioral strategies[5],of which the leader-follower strategy is widely used because of its significant advantage[6–8].In the virtual leader strategy[9,10],the whole formation system is regarded as an individual rigid body.The virtual leader formation system can be developed into a unit in a given direction and keep a rigid relative position between multiple vehicles.In the behavioral strategy[11,12],the control effect is determined by a weighted average of control corresponding to every vehicle expected behavior.Furthermore,three formation control strategies have their own strengths and weaknesses.In this paper,the leader follower strategy is adopted due to its simplicity and efficiency.

In the past years,lots of results with the consensus method can be found in various applications[13–15].A class of consensus methods for systems with second-order dynamics was introduced in[16],which expanded the first order consensus algorithms.Lin et al.[17]introduced a new technique taking advantage of the complex Laplacian to solve the problems of which the formation figures are appointed by inter-agent relative positions.Rezaeee et al.[18]managed the problem of cyclic pursuit for the multiagent system(MAS)in polygon formations.In all above works,the control inputs are unbounded.It means that the control inputs maintaining in a clearly defined bound cannot be ensured,which is determined by the agents actual control constraints.

Since the ability of any physical actuator is limited,actuator saturation is one of the most common and crucial nonlinearities in practical control systems[19,20].By comparing various performances of systems with saturation constraints,input saturation and actuator saturation,it can be concluded that input saturation only moderates long-term actuator saturation and avoiding actuator saturation is impossible in practical control systems[21].The control system subject to actuator saturation in the MAS has received considerable attention since actuator saturation cannot be avoided and it universally exists in various application areas[22].

Based on the existing results and motivated by the aforementioned statements,the finite-time control problems for MFV systems subject to actuator saturation is investigated.Apart from taking into consideration the actuator saturation,this paper solves the problem with a finite-time control tool.

The remainder of this paper is organized as follows. Section 2 gives a review on the mathematical tool that is necessary for the research.The formation control systems subject to actuator saturation is presented in Section 3.The finite-time formation controller is presented and developed in Section 4.Simulation results are provided in Section 5.The concluding statements are given in Section 6.

2.Preliminaries

2.1 Graph theory

The graphG=(v,ε,A)is introduced to describe the information sharing structure,v={1,2,3,...,N}is called the node set,ε⊂v×v={(i,j):i,j∈v}is called the edge set.The weighted adjacency matrixA=[aij]∈RN×N(i,j=1,2,...,N)is defined asaii=0,aij>0 when ij,aijis the weight of edge fromitoj.Besides,a diagonal matrixD=diag{d1,d2,...,dN}∈RN×Nwithis a degree matrix ofG.The matrixL=D−A∈RN×Nis the Laplacian of the weighted directed graphG.

2.2 Homogeneous theory

Before presenting the main results of this paper,some important lemmas are given first for further analysis.

Lemma1[23](LaSalle’sinvariance principle)Letx(t)be a solution of˙x=f(x),x(0)=x0∈Rn,wheref:U→Rnis continuous with an open subsetUof Rn,andV:U→R be a locally Lipschitz function such thatD+V(x(t))0,whereD+denotes the uppers Dini derivative.ThenΘ+(x0)∩Uis contained in the union of all the solutions that remain inS={x∈U:D+V(x)=0},whereΘ+(x0)denotes the positive limit set.

Definition 1Consider the system˙x=f(x),f(0)=0,wherex∈Rn,andf(x)=[f1(x),...,fn(x)]Tis a continuous vector field.Let(r1,...,rn)∈Rnwithri>0,(i=1,2,...,n).f(x)is said to be homogeneous of degreeκ∈R with respect to(r1,...,rn)if,for any givenε>0,fi(εr1x1,...,εrnxn)=εκ+rifi(x)(i=1,2,...,n),∀x∈Rn.The system˙x=f(x)is said to be homogeneous iff(x)is homogeneous.

Lemma 2[24]Consider the following system:

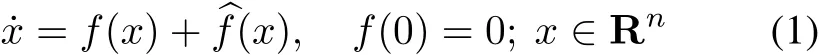
wheref(x)is a continuous homogeneous vector field of degreeκ<0 with respect to(r1,...,rn),and(x)satisfies(0)=0.Assumex=0 is an asymptotically stable equilibrium of the system˙x=f(x).Then,x=0 is a locally finite-time stable equilibrium of the system if

In addition,if the stable equilibriumx= 0 of the original system(1)is globally asymptotically stable,thenx=0 is a globally finite-time stable equilibrium of the system(1).

2.3 Accurate linearization by differential geometry

For the nonlinear system as

wherex∈Rn,u∈Rm.f(x)∈Rn,C(x)=[c1,...,cm]andgi(i=1,2,...,m)∈Rmare smooth vector fields,and

In the condition that the rank ofC(x)ism,(2)is linearizable if and only if it meets the following requirements:

(i)the dimension ofCi(0in−1)is constant nearbyx0;

(ii)the dimension ofCn−1isn;

(iii)Ci(0in−2)is involutive.Moreover,acjoffandcjis called therth Lie bracket,and{r1,...,rm}is

Since

there exists aϕ(x)=[ϕ1(x)···ϕm(x)]T,such that

and

is nonsingular on the neighborhoodTherefore,(2)can be converted into

(Hc,Mc)is in the form of the standard Brunovsky controller,which includes{r1,...,rm}.

The local diffeomorphism onV0is

and

The nonsingular state feedback is

whereα(x)is a smooth function fromV0to Rn,

β(x)is a nonsingular matrix onV0:

3.Formation control systems subject to actuator saturation

In this section,the formation control systems subject to actuator saturation is constructed.

3.1 Dynamic and kinematic model of flight vehicle

Assuming thatNflight vehicles in the formation system have the same structure,the dynamics of the flight vehicle are

wherei=1,...,Nis the index number of the flight vehicle.Vi,θi,ψVi,nxi,nyi,nziandgrepresent speed, flightpath angle,heading angle,overload components in three axes,and acceleration of gravity,respectively.

The kinematic equations are

where(xi,yi,zi)denotes the position of the flight vehicle in the inertial coordinate system.

3.2 Accurate feedback linearization

Select the state and control vector as follows,respectively:

(11)and(12)can be rewritten as

where

If and only if the demand in Section 2.3 is achieved,(15)is full-state-feedback linearizable.The distributionCi(i=0,1,...,5)is involutive in this paper.

A nonsingular smooth vector function is selected as follows,which satisfies(5)and(6):

Then the state feedback transformation is obtained:

where

Therefore,(15)can be converted into

where

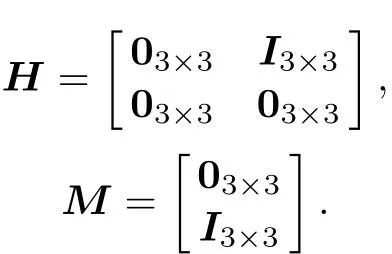
3.3 Coordination scheme for formation flying

In this section,the leader coordinateol−xlylzlis established,so the leader-follower relative coordinate can be obtained in Fig.1.

Fig.1 Leader-follower relative coordinate

The battlefield environment is changing rapidly,and the MFV system should complete the formation task in finite time.The leader of the system is equipped with a high performance seeker,and the followers are equipped with low-performance seekers.In general,there is only one leader,and other flight vehicles serve as followers.The configuration of the formation varies with the task.The process of formation control for the MFV system with actuator saturation can be described in Fig.2.The task of the MFV system is to intercept a moving target,and the detection and guidance accuracy can be improved by MFVs.Wedge-shape formation is suitable for the study of this paper.

Fig.2 Formation control based on consensus theory

3.4 Formation tracking control with actuator saturation

In this paper,the MFV system composed ofNflight vehicles is considered.Each flight vehicle exchanges its formation information with their neighbors by communication topology.The dynamics of theith flight vehicle which is subject to actuator saturation are described as

whereH∈R6×6andM∈R6×3are system matrices,which are the same as in(18),zi∈R6is the state of flight vehiclei,vi∈R3is the control input acting on the flight vehiclei,and sat:R3→R3is a saturation function deifned as

Equation(20)can be rewritten as

and

χi(vi)∈(0,1]can be denoted as a pointer for the level of saturation of the control input.Ifχi(vi)is close to 0,it means there is nearly no feedback from inputvi,andχi(vi)=1 means that does not saturate.

As 0<χi(vi)1,there exists a constantδsatisfying

Definition 2Finite-time formation problem of MFV with actuator saturation.Considering the MFV systems subject to actuator saturation described in(19),the subscriptlrepresents the leader,and subscript 1,...,N−1 denote the followers.Expected formation with actuator saturation can be achieved in finite time,if there existsT0∈[0,+∞),such that the MFV system in the leader following strategy satisfies

and

in any initial states,wherepiandqirepresent the position vector and the velocity vector of theith follower,respectively.didenotes the desired relative position vector.plandqldenote the position vector and the velocity vector of the leader,respectively.

In this work,the finite-time formation control problem with actuator saturation is concerned,and the block diagram is shown in Fig.3.A distributed finite-time formation controller is designed,which provides the control command based on mission requirements and neighborhood information.

Fig.3 Finite-time formation control structure with actuator saturation

Considering the actuator saturation,a control protocol can be derived that solves the formation problem of the MFV system.The position and velocity states of the flight vehicle are the information that they share with each other.

4.Formation controller design based on consensus theory

In this subsection,the focus is put on solving the finitetime formation control problem for the MFV systems subject to actuator saturation.The tracking error dynamics of the flight vehicles are derived,in which the desired positions of the flight vehicles are described.Then a formation control protocol is developed via the finite-time consensus theory.With the aid of the homogeneous theory,the stability of the finite-time formation control system is analyzed.

4.1 Tracking error dynamics

It can be shown that the dynamics of theith flight vehicle can be rewritten as

Then(24)can be descripted as

Therefore,the nonlinear system composed of(11)and(12)is transformed into a linear double-integrator system(25)with actuator saturation,so the research and design processes are greatly simplified.

Assumption 1The position and velocity of flight vehicles can be measured.

Assumption 2The leader could plan its trajectory autonomously.

represents the desired position in the coordinate frameoI−xIyIzIfor theith follower flight vehicle.

whereplrepresents the leader’s position,δ(θl,ψVl)denotes the coordinate transformation matrix fromol−xlylzltooI−xIyIzI.represents the desired position inol−xlylzlfor theith follower.

The tracking erroreican be shown as

wherevfiis the control input which needs to be designed to stabilize error dynamics,Ei=eiT,HandMare the same as those in(18).Furthermore,

4.2 Formation tracking law based on finite-time control

Suppose that there arenfollowers(labelled as 1 ton)and one leader(labelled as 0)denoted as in the group.The objective of this subsection is to design a bounded control lawvfxifor all the followers such that the desired formation configuration in the presence of actuator saturation can be achieved in finite time.

Assumption 3For a communication graph which contains a directed spanning tree with the leader as the root,its subgraph associated with the followers is undirected.

For convenience,let

and sig(x)α=|x|αsign(x),where sign(·)denotes the sign function and|x|denotes the absolute value of the real numberx.

Theorem1When Assumption3 holds,considering the formation tracking control system(19),the control variablevfxiin thexdirection can be given as

where

vfxican realizein finite-time,if there exists a continuous odd functionsϕrsatisfyingxϕr(x)>0(∀x=0),andϕr(x)=εrx+o(x)aroundx=0 for some constantεr>0(r=1,2,3,4).Moreover,vi∞vmax.k1andk2are the feedback control gains,

In this paper,suppose that the positions and velocities are measurable,and the flight vehicles are subject to actuator saturation such thatvi∞vmax.It can be seen that the control protocol(31)accounts for the actuator saturation,due to the boundedness of the saturation function sat(·).

Likewise,vfyiandvfzican be derived as

where

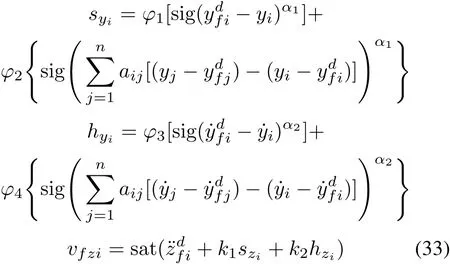
where

The control law of three channels can be rewritten as

where

vfican help the control system(19)with actuator saturation achieve the desired formation.

Therefore,the final formation tracking control variableufiof theith follower is

whereβ−1(x)andα(x)can be derived by(17).

4.3 Finite-time stability analysis by homogeneous theory

where

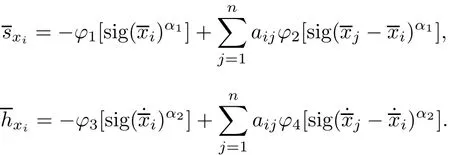
As(21)shows,(36)becomes

Therefore,

ProofConsider the Lyapunov function as

Then

Thus,one can get

As the odd function satisfyingϕr(x)=εrx+o(x)(r=1,2,3,4),the formation control protocol(31)can be rewritten awith

Also,by choosing 0<α1<1,α2=,the system(36)with variablesis homogeneous with dilation

Finally,after the analysis and derivation,one can easilyget the fact thatsatisfies

To sum up,the system(36)is globally asymptotical stable and locally homogeneous.Consequently,the origin is a finite-time stable equilibrium point of the system(36)by Lemma 2.Hence,the origin is a globally finite time stable equilibrium point of the system(8),that meansin finite time.

5.Simulation results

The finite-time formation of three flight vehicles with actuator saturation is investigated in this paper.Three flight vehicles have different roles,one leader and two followers.Two instances are considered to test the performance of the designed formation control law.Triangle formation is selected,and the topology is given in Fig.4.Obviously,this communication topology satisfies Assumption 3.The initial condition of flight vehicles is shown in Table 1.

Fig.4 Communication topology of flight vehicles

Table 1 Initial condition of flight vehicles

The expected formation positions are

The main controller parameters are

andis set as 40 m/s2,ϕ1(x)=ϕ2(x)=ϕ3(x)=ϕ4(x)=x.The control parameters in theydirection and thezdirection are the same as in thexdirection.

Case 1The leader flight in a fix acceleration.

In this case,the leader vehicle flight at a uniform acceleration is

The trajectory of flight vehicles is plotted in Fig.5.In Fig.6,the position track errorseicould decrease,and come to zero rapidly,the convergence time is about 6.5 s.The bounded control inputvfxi,vfyiarevfziare also given in Figs.7–9.It is obvious from these plots that for the given initial state,the control inputs decrease as the values of the tracking errors decrease,and without exceeding their control actuation limits,which indicates that the designed control protocol with actuator saturation is effective.Figs.10–12 show the origin control input of the followers,and it can be seen from Figs.13–15 that followers could track states of the leader successfully.

Fig.5 Flight trajectories in Case 1

Fig.6 Position track errorseiin Case 1

Fig.7 Bounded control input vfxiin Case 1

Fig.8 Bounded control input vfyiin Case 1

Fig.9 Bounded control input vfziin Case 1

Fig.10 Origin control input ufxiin Case 1

Fig.11 Origin control input ufyiin Case 1

Fig.12 Origin control input ufziin Case 1

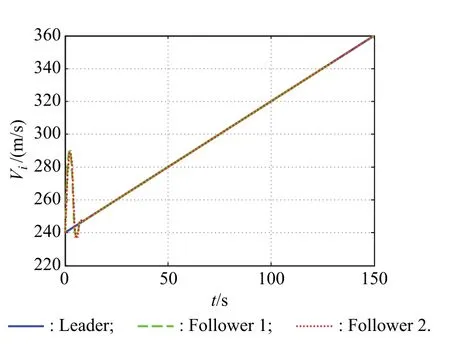
Fig.13 Velocity Viin Case 1

Fig.14 Flight-path angle θiin Case 1

Fig.15 Heading angle ψViin Case 1

Case 2The leader flight in a sine law.

In this case,the state of the leader flight is changing continually.

For the simulation results of Case 2,clearly,with the leader flight in a sine law,followers should adjust their states to achieve the desired formation configuration.From Fig.16,it can be seen that the flight vehicles could fly in the expected formation form in the final phase,which guarantees three flight vehicles accomplish the cooperative combat task.It can be seen from Fig.17 that the position tracking errors come to zero at around8.5 s.Therefore,the designed formation control method is also effective for the case with a maneuver leader,but it takes a little longer time than Case1.Figs.18–20 show that the bounded control inputs of the followers could adjust their states such that the formation can be achieved.However,the bounded control input curves of followers no longer tend to flat,but change continuously with the leader maneuvering flight.The origin control inputs of the followers in Figs.21–23 also verify it.It can be seen that the velocityVi,the flight-path angleθiand the heading angleψVicould also reach agreement in Case 2 as shown in Figs.24–26.

Fig.16 Flight trajectories in Case 2

Fig.17 Position track errorseiin Case 2

Fig.18 Bounded control input vfxiin Case 2

Fig.19 Bounded control input vfyiin Case 2

Fig.20 Bounded control input vfziin Case 2

Fig.21 Origin control input vfxiin Case 2

Fig.22 Origin control input vfyiin Case 2

Fig.23 Origin control input vfziin Case 2

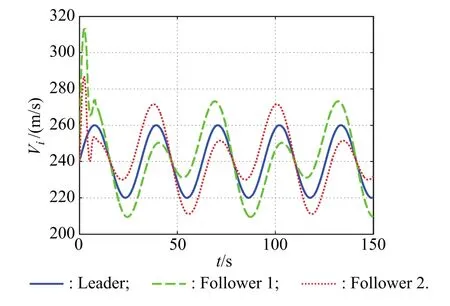
Fig.24 Velocity Viin Case 2

Fig.25 Flight-path angle θiin Case 2

Fig.26 Heading angle ψViin Case 2

From the simulation results,it can be concluded that the designed formation control law with actuator saturation is effective for a maneuver leader,but the tracking time is longer than the instance of the straight flight leader.In addition,the states of the leader change continuously in Case 2,and the MFV system could still maintain the expected formation.

6.Conclusions

In this paper,the finite-time formation control problem subject to actuator saturation has been investigated for MFV systems.For the considered systems,a precise linearization model is obtained by principles of differential geometry for the flight vehicle.A class of saturated finite-time formation control protocols are first proposed based on both relative position and relative velocity measurements under directed communication topologies.The finite-time stability of the formation tracking system is analyzed by the homogeneous theory for network topologies that contain a spanning tree.Finally,simulation results have been shown to illustrate the effectiveness of the proposed method.