大功率往复泵曲轴转子动力学特性研究*

□ 张俊峰 □ 张春光 □ 刘光恒 □ 刘佳慧 □ 褚 帅 □ 安 磊

沈阳仪表科学研究院有限公司 沈阳 110043

1 研究背景

随着社会的发展与基建规模的扩大,大功率往复泵的需求不断提升。大功率往复泵利用高压水射流对钢筋混凝土破拆,不损坏钢筋,广泛应用于道路施工、桥梁改建、高速公路维护、市政工程等领域,成为近几年工程领域的一大新热点。曲轴是大功率往复泵动力端的关键零部件,其质量往往直接影响大功率往复泵的性能。随着大功率往复泵功率的提高,曲轴性能的要求也越来越高。曲轴是一种典型的旋转机械,对其进行转子动力学设计是重要环节,临界转速、转子不平衡响应和转子启动轴心轨迹是研究的重点。近年来,随着计算机计算性能的显著提高,利用有限元法来分析转子动力学特性已成为一种主流工程方法[1]。在有限元模型中考虑转动惯量、陀螺力矩、轴向载荷等因素的影响,使计算相较于其它方法精度更高。笔者采用有限元法对大功率往复泵曲轴转子进行动力学特性研究。

2 泵动力端三维模型

笔者对转子轴承系统建立动力学模型,一般将转子系统简化为弹性轴段、离散刚性圆盘及轴承支撑单元[2],各单元之间由节点连接,进而建立系统的总运动方程。

根据大功率往复泵的性能,对泵动力端整体传动方案和关键零部件进行设计,并利用计算机辅助设计软件进行三维模型构建。泵动力端三维模型如图1所示,其中曲轴采用五拐四支撑布局。曲轴转子三维模型如图2所示,主要尺寸参数见表1。

3 刚性圆盘运动方程

设圆盘中心节点的广义坐标{u1d}=[x,θy]T,{u2d}=[y,-θx]T,刚性圆盘质心与轴心重合,根据拉格朗日定理,刚性圆盘的运动方程为:

(1)

(2)

(3)

式中:Ω为回转体的角速度;{Q1d}、{Q2d}为广义力;m为刚性圆盘质量;Jd为过轴心的径向转动惯量;Jp为极转动惯量。

4 弹性轴段运动方程

设弹性轴段单元广义坐标{u1s}=[xA,θyA,xB,θyB]T,{u2s}=[yA,-θxA,yB,-θxB]T,根据拉格朗日定理,轴段单元的运动方程为:

(4)

[Ms]=[MsR]+[MsT]

(5)

式中:[Ms]为包含转动惯性矩阵与移动惯性矩阵的质量矩阵;[MsR]为转动惯性矩阵;[MsT]为移动惯性矩阵;[Js]为回转矩阵;[Ks]为弹性轴段刚度矩阵。

根据弹性力学有限元法,曲轴转子在笛卡儿坐标系中的运动微分方程为:

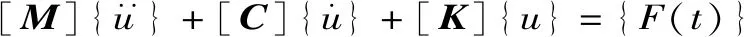
(6)

式中:[M]为总体质量矩阵;[K]为总体刚度矩阵;[C]为由阻尼矩阵和陀螺力矩阵组成的矩阵;{F(t)}为外部激振力。

5 曲轴转子有限元模型

将曲轴转子支撑系统作为研究对象。曲轴转子为五拐四支撑结构布局,采用SOLID185单元类型,单元数为503 243,节点数为195 929,网格质量达到计算精度要求。轴承采用COMBI214单元类型模拟,这一单元类型可以模拟交叉刚度和阻尼,还能模拟拉压刚度,但不能模拟弯曲或扭转刚度。曲轴材料弹性模量为210 GPa,密度为7.8×103kg/m3,泊松比为0.3。模型Z方向为曲轴转子旋转方向,假设轴承各向同性,且不受阻尼影响。

在曲轴转子四个支撑位的截面中心建立主节点,在截面外圆周建立从节点,创建刚性区域。在每个支撑位置通过创建COMBI214单元来模拟轴承,单元某一端与刚性区域主节点相连,另一端施加全约束。曲轴转子有限元模型如图3所示。

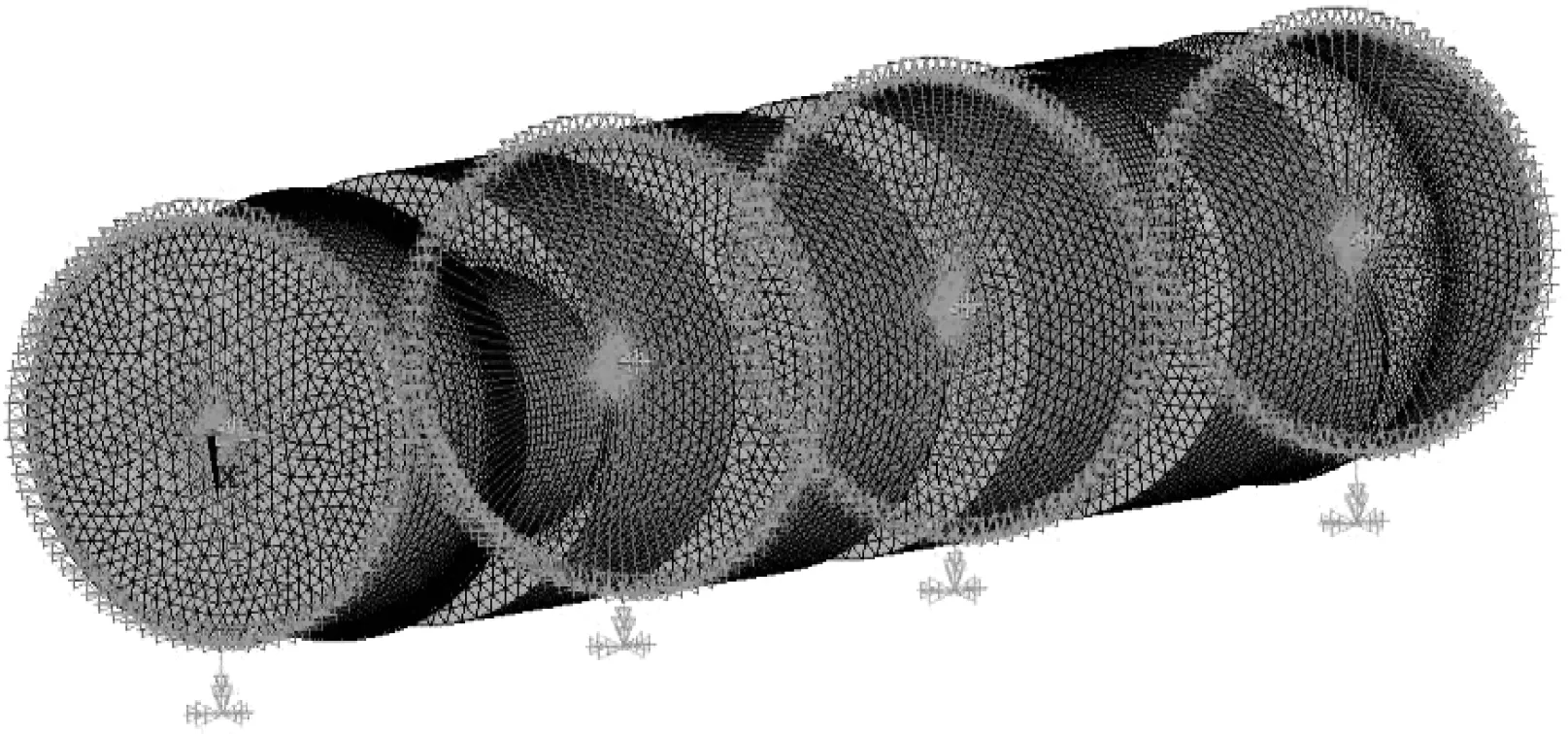
▲图3 曲轴转子有限元模型

6 模态分析

大功率往复泵曲轴转子是典型的旋转零件,相较于一般零部件,模态分析时需考虑陀螺效应对转子的影响[3-5],应将陀螺效应设置为打开。笔者使用QR阻尼法对转子系统进行模态分析,这一方法可以很好地对低阻尼系统进行求解,支持不对称阻尼和不对称刚度。计算得到曲轴转子前六阶固有频率见表2,前六阶模态振型如图4所示。

▲图4 曲轴转子前六阶模态振型

由于考虑到陀螺效应,曲轴转子转速对特征频率有一定影响。计算不同转速所对应的固有频率,并绘制固有频率随转速变化曲线,这一曲线图称为坎贝尔图[6-8]。在坎贝尔图上,从纵轴出发曲线斜率为正的直线代表正进动,斜率为负的直线代表反进动,从原点出发的转速直线与正进动直线相交点所对应的横坐标代表临界转速。一般计算临界转速时只考虑正进动转速。

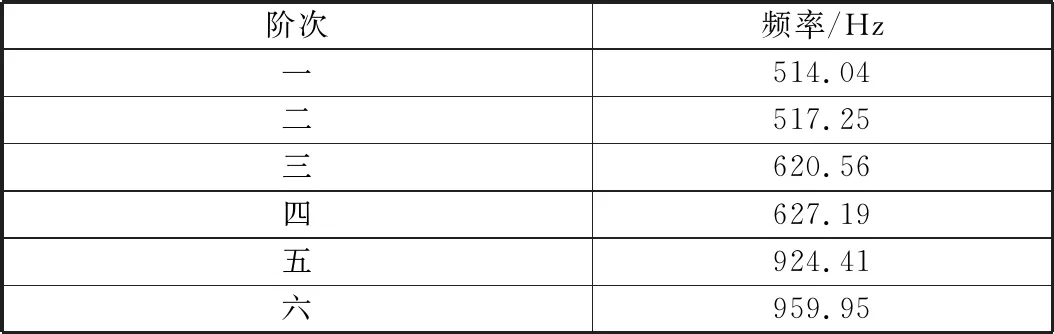
表2 曲轴转子前六阶固有频率

载荷步分为40步,转速为0～600 r/min,利用模态分析绘制曲轴转子坎贝尔图,如图5所示。

在图5中可以看到,从原点出发的转速直线并没有与正进动直线相交,也就是说曲轴转子工作转速没有达到临界转速,旋转结构不会产生共振,运行安全,满足设计要求。

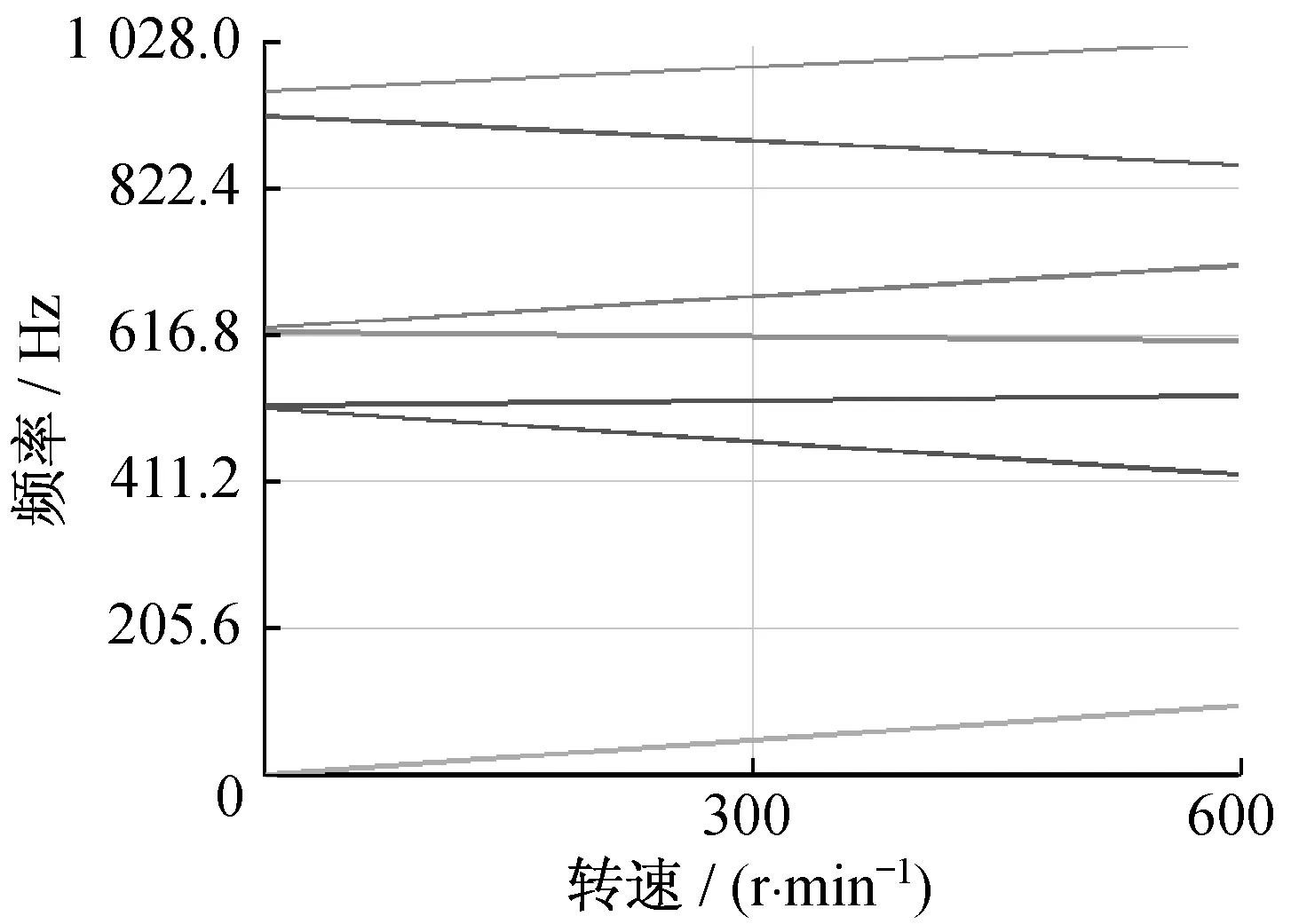
▲图5 曲轴转子坎贝尔图

7 不平衡响应分析

由力学知识可知,大功率往复泵曲轴转子由于质量偏心引起的离心力F为:

F=meω2

(7)

式中:m为偏心质量;e为偏心距;ω为曲轴转子转速。

在理想情况下,无需考虑轴向力,离心力被分解为X方向与Y方向的减谐力,为:

(8)

式中:t为时间。

利用有限元法进行不平衡分析[9],打开陀螺效应,设置不平衡响应的频率为0～1 500 Hz,子步数为40。经分析得到曲轴转子不平衡响应结果,如图6所示,横坐标为扫频频率,纵坐标为曲轴转子轴心的振动幅度。曲轴转子在525 Hz、637.5 Hz、900 Hz、1 200 Hz、1 425 Hz频率处振动幅度较大,即在这些频率处产生较强共振,与模态分析的结果基本相同,由此验证了模态分析的准确性。

▲图6 曲轴转子不平衡响应结果

8 启动过程响应分析

大功率往复泵曲轴转子由电机驱动,启动时间较快,1 s时间从0加速到39.76 rad/s,随后进入稳定转速状态。曲轴转子启动时角速度变化如图7所示。

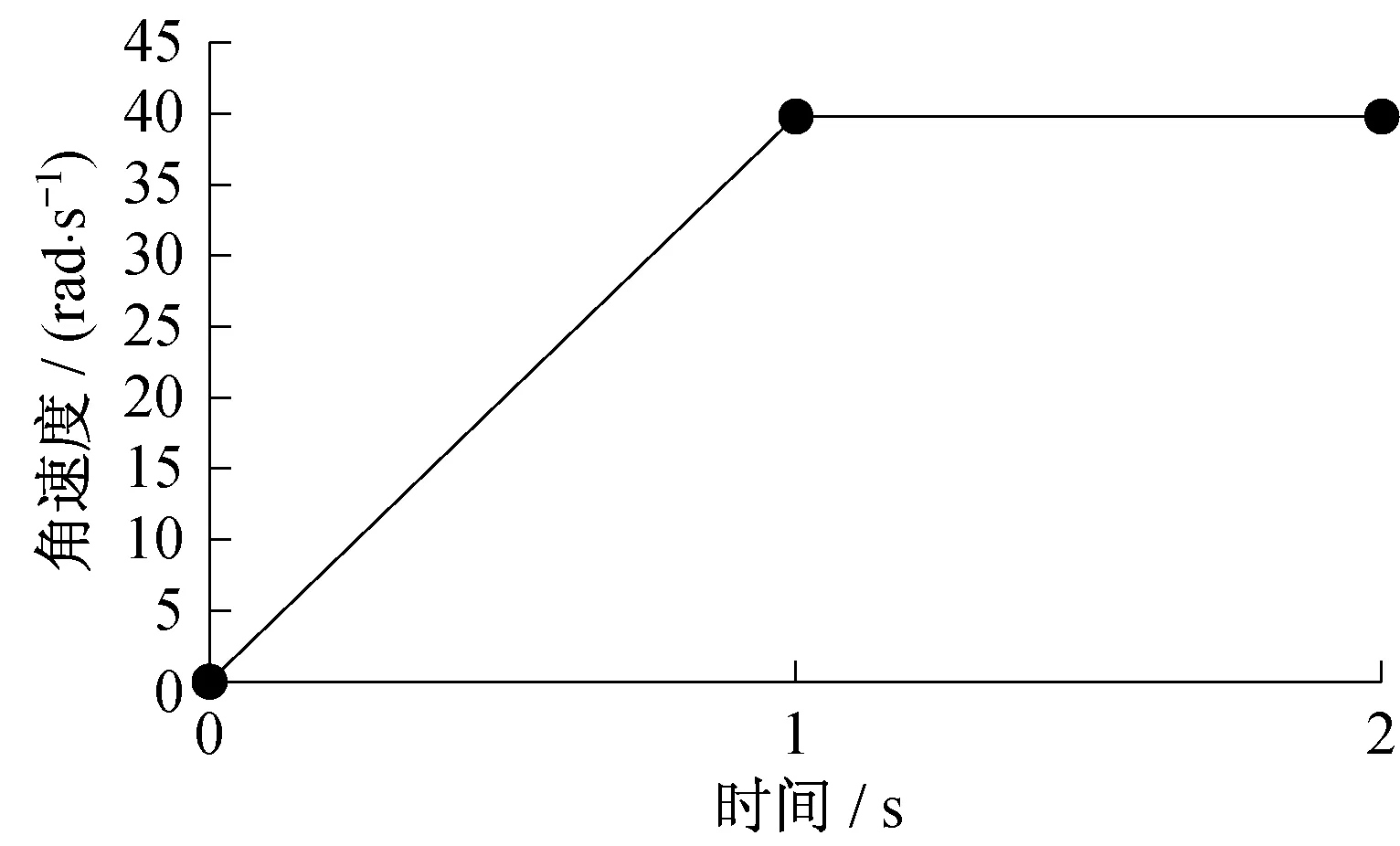
▲图7 曲轴转子启动时角速度变化

整个加速过程中角加速度为39.76 rad/s2。曲轴转子动不平衡等级选择为G6.3,由此得到曲轴转子加速过程中的激振力为:

(9)

对曲轴转子进行瞬态动力学响应分析,得到曲轴转子轴心的运动轨迹,如图8所示。从图8中可以看到,曲轴转子轴心的最大响应振幅为4.72×10-8m,振幅很小,没有产生共振,并且轴心的运动轨迹经过启动时螺旋线后达到稳定运行状态,近似圆形运动轨迹,符合预期要求。

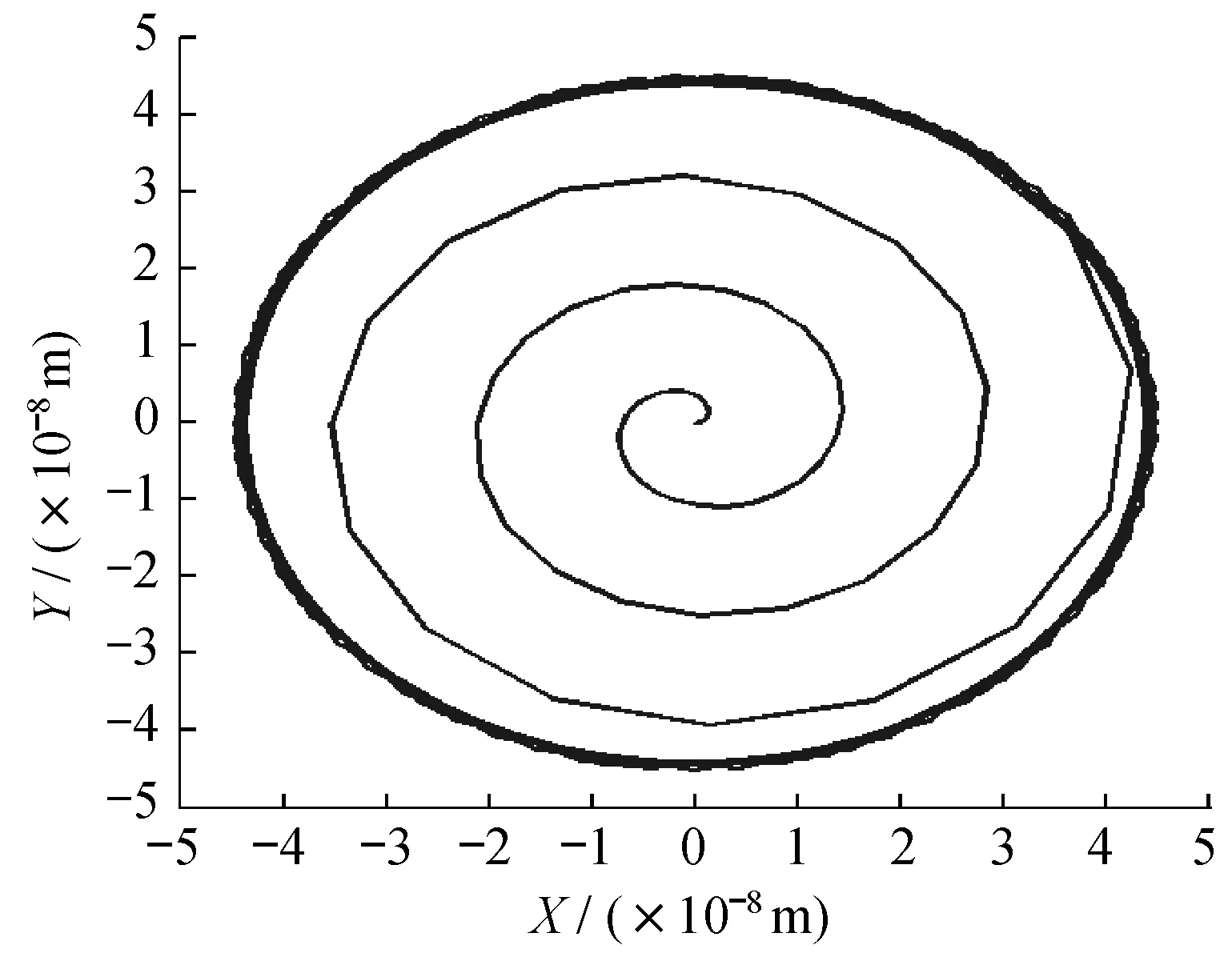
▲图8 曲轴转子轴心运动轨迹

9 结束语

为了验证大功率往复泵曲轴转子设计的合理性,笔者对曲轴转子进行了模态分析、坎贝尔图分析、不平衡响应分析与启动过程响应分析。

对曲轴转子进行模态分析,得到曲轴转子的前六阶固有频率及振型,充分了解了曲轴转子的振动情况,为设计验证提供依据。

对曲轴转子进行坎贝尔图分析,发现从原点出发的转速直线并没有与正进动直线相交,也就是说曲轴转子工作转速没有达到临界转速,旋转结构不会产生共振,运行安全,满足设计要求。

根据计算的不平衡量对曲轴转子进行不平衡响应分析,得到不平衡响应结果及共振频率点,确认与模态分析的结果基本相同,验证了模态分析的准确性。

对曲轴转子进行启动过程响应分析,得到启动瞬间与稳定运行时的运动轨迹,确认曲轴转子轴心的振动幅度很小,没有出现共振情况,由此验证了设计的合理性。