Al/Ni 类含能结构材料冲击压缩特性细观模拟

2020-10-31张先锋陈海华谈梦婷

含能材料 2020年10期

熊玮，张先锋，陈海华，杜宁，包阔，谈梦婷

（南京理工大学机械工程学院，江苏南京 210094）

1 引言

Al/Ni 材料是典型的含能结构材料（Energetic structural materials），同时具备结构特性和化学反应释能特性。该类材料在一般情况下保持惰性且不相互反应，当给予足够的机械、电或激光等刺激后会迅速释放大量的化学能，发生快速燃烧或爆炸［1］。由于兼具含能和强度特性，含能结构材料在军事领域和民用领域均具有十分广阔的应用前景［2-6］，如制作含能破片、含能药型罩、基于含能结构材料的侵彻体及空间碎片防护结构等。在材料制备方面，由于Al/Ni 类含能结构材料在温度达到铝的熔点（660 °C）时即会发生化学反应，一般不采用烧结［7-8］和高温熔融的方法制备该种材料，因此最常用的制备方法有准静态压制［9-10］、爆炸合成［11］和冷轧［12］等。

相关研究表明［13］，Al/Ni 类含能结构材料的细观结构（颗粒尺寸、形状以及颗粒分布等）对其力学行为及冲击反应特性的影响十分显著。在细观尺度上建立含能结构材料的冲击响应模型，研究其在冲击压缩下的金属颗粒材料间的碰撞、孔隙压垮、接触面变化及温度分布等规律，能更直接分析含能结构材料的冲击动态力学响应特性，进而有利于阐明其冲击反应机制。含能结构材料细观模型的生成方法主要有两种：（1）满足分布统计规律的细观数值仿真模型。Williamson［14］将不锈钢材料简化为在细观尺度上由均匀、等粒径颗粒构成，生成了相应细观数值仿真模型。为了更接近真实细观分布情况，Benson［15-16］、Austin等［17-19］和乔良［20-21］随后改进了该类细观模型建立方法，结合材料中颗粒细观分布特性（材料配比、尺寸、几何形态）建立相应的数学描述，并利用随机数生成方法、模拟退火算法等方法生成满足细观分布统计规律的模型。（2）基于细观照片生成细观尺度数值仿真模型。Eakins［22-23］通过（Scanning Electron Microscope，SEM）设备得到了Al/Ni 含能结构材料的细观照片，并以此建立了细观尺度数值仿真模型，研究了材料颗粒形状和密实度等细观特性对Al/Ni 类含能结构材料冲击响应行为的影响规律，同时确定了其状态方程参数，其建模过程主要有三步［23］：区分相、矢量化、导入仿真软件。相比而言，满足分布统计规律的细观数值仿真模型的建立更加方便快捷，而基于细观照片生成细观尺度数值仿真模型更能体现材料细观尺度上的实际分布特点，而两种建模方法对含能结构材料冲击响应细观模拟结果的影响机制仍有待探索。

基于以上研究背景，本研究选取三种典型的Al/Ni类含能结构材料为研究对象，结合细观结构照片和细观颗粒初始形态建立该类材料的冲击压缩细观模型，重点关注冲击压缩过程中的材料颗粒变形、压力响应及热点分布、冲击波传播特性等问题，分析两种建模方法对材料冲击压缩响应特性的影响机制，为含能结构材料冲击反应特性的研究奠定基础。

2 细观模拟方法

2.1 典型Al/Ni 类含能结构材料的细观结构特性

对不同Al/Ni 类含能结构材料的细观结构观测有助于确定材料细观结构参数，研究细观结构参数对材料力学行为及冲击反应特性的影响规律，同时也可为后续细观仿真建模提供参考。三种典型Al/Ni 类含能结构材料SEM 照片如图1 所示。前两种材料为Al/Ni粉末复合材料，由初始粒径分别小于23 μm 和75 μm的Al 粉和Ni 粉按一定比例混合后，通过粉末压制法制备得到，尺寸为Φ10 mm×10 mm。其中，1#材料体积配比为50/50，记为Al/Ni（VAl/VNi=50/50）粉末复合材料；2#材料化学计量比为50/50，记为Al/Ni（nAl/nNi=50/50）粉末复合材料。3#材料为Al/Ni（nAl/nNi=50/50）多层复合材料，由初始厚度分别为0.8 mm 和0.5 mm 的Al板和Ni板交叠后轧制而成，随后切割为Φ11.8 mm×5.5 mm圆柱型试样。

对于1#材料，在SEM 照片（图1a）中Al 球形颗粒均匀分布在Ni 基质中，其Al-Al 晶界较为清晰。而2#材料SEM 照片中，Al 颗粒相互结合，Al-Al 晶界不够分明。这是由于随着Al 含量增加，Al-Al 颗粒间发生相互接触，在准静态压制过程中发生变形并结合在一起，形成如图1b 所示的团聚现象。另一方面，图1c 所示基于冷轧技术制备的3#材料的细观结构主要以Al 为基体，而Ni 平行散布其中。同时，由于Al 和Ni 的可压缩性不同，两者在轧制过程中的厚度比发生了改变。

图1 三种典型Al/Ni 类含能结构材料细观结构Fig.1 The microstructures of three typical Al/Ni composites

2.2 细观几何模型的建立方法

2.2.1 基于SEM 照片的细观几何模型生成方法

为了反映Al/Ni 类含能结构材料真实的细观结构特性，利用SEM 照片建立了细观几何模型［24］，截面如图2 所示。通常，SEM 拍摄的区域有限，代表性体积单元（Representative volume element，RVE）的尺寸过小，不足以模拟整个冲击压缩过程中材料细观尺度上的变形行为及冲击波传播规律，因此需要采用适当的方法获取尺寸更大的细观模型。对于Al/Ni 粉末复合材料（1#、2#），由图1 可知，其颗粒分布具有随机性，即该材料的细观结构具有各向同性的特性。将基于SEM得到的矢量图沿x、y两个方向分别进行镜像处理，最终得到细观几何模型的截面尺寸为1 mm×1 mm。

对于Al/Ni 多层复合材料（3#），Al、Ni 两相的细观结构均为细长型，近似于平行分布。在相关试验中［25］，受力方向通常与轴线方向平行（即与细观尺度Al-Ni 界面垂直）。由于拍摄角度问题，SEM 照片与试件轴线呈一定的夹角。因此，需将所得到的RVE 进行旋转，使之与实际受力情况相符合。同时，由于Al/Ni多层复合材料的颗粒较大，所建立的细观几何模型尺寸需要大于粉末复合材料的尺寸，以消除边界效应的影响。将所得到的矢量图进行镜像或平移，得到截面尺寸为5 mm×5 mm 的细观几何模型。将基于SEM 得到的模型截面沿其垂直方向拉伸，最终得到具有真实细观结构特性的Al/Ni 类含能结构材料切片，用于模拟Al/Ni 类含能结构材料中任一横截面切片中的冲击波传播过程。

图2 基于SEM 照片建立的三种典型Al/Ni 类含能结构材料细观仿真模型Fig.2 The mesoscale model established based on SEM images for three typical Al/Ni composites

为了验证上述建模方法得到的Al/Ni 类含能结构材料细观模型材料配比与真实材料的一致性，通过提取细观模型中各细观相的体积，从而获取细观模型中Al 的体积百分数，如表1 所示。将细观模型中Al 的体积分数与材料制备时的体积分数进行对比可以发现，两者误差不超过10%，说明本研究所选取的几种Al/Ni 类含能结构材料RVE均能够反映材料内部的真实情况。

表1 三种Al/Ni 材料细观模型与真实材料中Al 的含量对比Table 1 Comparison of the volume fraction of Al in mesoscale model and real material %

2.2.2 基于颗粒初始形态的Al/Ni 类含能结构材料均匀化细观几何模型

在含能结构材料冲击响应特性细观模拟中，最常用的方法是结合材料中初始颗粒细观分布特性（材料配比、尺寸、几何形态）建立满足分布统计规律的细观数值仿真模型。因此，本研究按照材料颗粒的初始形态特征对几种典型的Al/Ni 类含能结构材料进行了均匀化细观建模，用于与基于SEM 照片生成的细观模型的对比研究。

基于1#和2#材料的细观结构特征（图1），在均匀化细观几何模型中，将Ni 设置为基体材料，而Al 按照其颗粒初始形态建立为等粒径（R=11.5 μm）的圆形颗粒。Al 颗粒的位置（xi，yi）按照随机分布方法进行分配［21］，在此过程中需保证颗粒间互不重叠：

对于3#材料，由SEM 照片（图1）可知，其细观层近似于平行分布。保持Al、Ni 细观层厚度比为原始材料层厚度比（1.6∶1），取Ni 的厚度为0.2 mm，可建立Al/Ni 多层复合材料细观模型。三种典型Al/Ni 类含能结构材料的均匀化细观模型截面如图3 所示。

图3 Al/Ni 类含能结构材料均匀化细观仿真模型Fig.3 The mesoscale model established with homogenization method for three typical Al/Ni composites

虽然此方法建立的Al/Ni 类含能结构材料细观模型材料配比与其真实材料配比完全一致，但是，通过与细观结构照片对比可以发现，基于材料初始颗粒形态的均匀化细观几何模型既无法体现Al/Ni 粉末复合材料（1#、2#）在制备过程中发生的变形和团聚现象，也无法体现Al/Ni 多层复合材料（3#）在轧制过程中两相厚度比的改变及Ni 相的断裂，与材料真实细观结构存在较大差异。

2.3 材料模型

Johnson-Cook（J-C）模型［26］是常见的用于描述金属材料在大变形、高应变率和高温情况下热力学行为的材料模型。该模型具有形式简单、准确性好且相关材料参数容易从单项试验中获得等优点。本研究选取Johnson-Cook（J-C）模型描述高应变率下Al、Ni 材料的力学行为，其表达式为：

式中，σe为等效应力，Pa；εe为等效应变；为无量纲塑性应变率；ε˙0为参考应变率，s-1；T*=(T-Troom)/(Tmelt-Troom)为无量纲温度；Y是参考应变率下的屈服强度，由准静态拉伸试验确定，Pa；B，n′，c和m′是材料常数。定义G为材料的剪切模量，Pa；λT为导热系数，W·m-1·K-1。材料参数［27-33］列于表2。

表2 Al、Ni 材料的参数Table 2 Material parameters for the constitutive model

Al、Ni 的冲击响应行为由Mie-Grüneisen 状态ε˙*=ε˙e/ε˙0方程［34］描述，该方程是常用的一种描述固体在冲击波高压条件下行为的物态方程，被广泛地使用来描述材料冲击压缩后的状态。其表达式为：

式中，C0是声速，m·s-1；S为材料常数。

2.4 求解器及算法选择

本研究主要采用ABAQUS/EXPLICIT 求解器模块对Al/Ni 类含能结构材料细观尺度下冲击响应特性进行仿真模拟。该求解器适用于求解非线性动力学问题和准静态问题，特别在模拟短暂、瞬时的动态事件（如冲击和爆炸问题等）具有一定的优势。同时，考虑到材料在高速冲击的高应变率条件下将发生剧烈变形，本研究采用欧拉算法对Al/Ni 类含能结构材料在冲击压缩条件下的动态响应行为进行仿真模拟。为了对冲击引起的温升进行准确计算，选取温度-位移耦合算法，网格形状为八节点正六面体（EC3D8RT），各材料初始温度为300 K。对于1#和2#材料，为了保证计算精度将欧拉域网格尺寸取为2 μm。另一方面，对于3#材料，由于其颗粒尺寸约为1#和2#材料的10 倍，为了提高计算效率，将其细观模型的欧拉域网格尺寸取为10 μm。此外，为了模拟冲击波的一维传播过程并减少计算时间，欧拉域的厚度方向尺寸取为一个网格大小。对欧拉域的材料属性进行定义，并基于前述得到的细观尺度几何模型，对每个网格进行物质分配。

2.5 边界条件

在细观模型的左侧建立刚性板，取其网格大小与欧拉域一致。刚性板以300～1500 m·s-1恒定速度对Al/Ni材料的细观模型进行压缩，则材料中的粒子速度Up即为刚性板的压缩速度。由于细观模型尺寸小于实际试样尺寸，为了模拟理想周期性材料细观结构和一维压缩条件，在除加载面以外的各个面均施加对称边界条件。

3 结果与讨论

为了研究典型Al/Ni 类含能结构材料细观热力学响应结果，对2#和3#两种具有典型细观结构的Al/Ni材料在冲击压缩过程中的颗粒变形、压力分布及温度分布情况进行分析。为了保证对比的有效性，本研究所示均为冲击波传播至细观模型相同位置（冲击压缩方向中点附近）的计算结果。同时，对三种典型Al/Ni复合材料冲击Hugoniot 参数进行计算。

3.1 典型Al/Ni 粉末复合材料冲击压缩细观模拟计算结果

3.1.1 细观颗粒变形情况

在三个典型冲击压缩速度下，基于SEM 照片建立的2#材料细观模型中颗粒变形情况如图4 所示。由于Al/Ni 粉末颗粒尺寸太小，此处对局部区域进行放大处理，并保证图片具有相同放大比。从计算结果可以看出，Up=300 m·s-1时，材料内部的细观颗粒无明显变形。随着Up上升至1200 m·s-1，颗粒变形逐渐剧烈。同时，在冲击加载条件下，材料体积发生了压缩。Up从300 m·s-1上升至1200 m·s-1的过程中，原始横向冲击压缩方向）尺寸为0.45 mm 的区域压缩为0.35 mm，相对压缩率为22.2%。因此，冲击压缩下的材料内部主要发生了颗粒变形和体积压缩两个过程。

另一方面，基于材料颗粒初始形态的2#材料均匀化细观模型冲击压缩颗粒变形情况如图5 所示。计算结果表明，在冲击加载条件下，初始颗粒形状规则且尺寸均匀的Al 颗粒发生了变形。当冲击速度达到800 m·s-1以上时，能够明显观测到Al 颗粒的大变形及颗粒间的融合现象。由于2#材料的真实细观结构中，Al 颗粒间存在团聚现象，因此通过粉末压制法制备的材料实际颗粒尺寸大于材料粉末的初始尺寸。而图5 所示细观模型的初始状态中，Al 颗粒间相互间隔且保持初始颗粒尺寸，在冲击压缩过程中的变形相比于基于SEM 照片建立的细观模型计算结果更加剧烈。

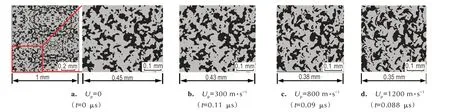
图4 2#材料在不同冲击压缩速度下的颗粒变形情况Fig.4 The deformation of particles in material 2# at different particle velocities based on the mesoscale model

图5 2#材料均匀化细观模型在不同冲击压缩速度下的颗粒变形情况Fig.5 The deformation of particles in material 2#at different particle velocities based on the mesoscale model with uniform particles

3.1.2 冲击压力及温度计算结果

图6 为不同冲击条件下基于SEM 照片建立的2#材料中压力和温度分布情况。从图6 可以看出，材料内部压力和温度分布不均匀。随着Up从300 m·s-1提高至1200 m·s-1，冲击压力最高值从8.8 GPa 上升至52.5 GPa，同时冲击温度最大值从452 K升高至2118 K。冲击压缩过程中，材料温升的主要来源是颗粒变形产生的塑性功和冲击压缩引起的体积压缩功。因此，冲击压缩速度越高，颗粒变形和体积压缩越显著，材料内部的冲击温度越高。假设Al/Ni 类含能结构材料的冲击反应过程主要是由温度控制的。当冲击温度超过反应阈值时，该材料发生部分化学反应，反应速率随温度的升高而增高，直至达到最大值，实现完全化学反应［27，36］。从细观仿真的角度进行分析，可以推论：冲击速度的增加可以促使冲击温度升高，从而加快化学反应速率，最终释放出更多的能量。这一推论与相关试验的结果吻合［25，37］。

2#材料均匀化细观模型在不同冲击压缩速度下的压力和温度分布情况如图7 所示。当Up从300 m·s-1升高至1200 m·s-1时，最大冲击压力从8.5 GPa 升高至54.7 GPa，相应的最大冲击温度从447 K 升高至2265 K。与由SEM 照片建立的细观模型计算结果相比，该模型计算的2#材料中细观尺度压力和温度峰值差异不大，但分布压力场和温度场的分布更加均匀。当Up达到800 m·s-1时，冲击波波阵面后局部温度超过Al 的熔点（933 K），Al 颗粒发生了局部变形，并与相邻颗粒产生融合。随着冲击速度的增大，材料内部温度更高，因此Al 颗粒的变形和融合现象更加明显。

图6 2#材料细观模型在不同冲击速度下的压力及温度分布Fig.6 The pressure and temperature response in material 2# at different particle velocities based on the mesoscale model

图7 2#材料均匀化细观模型在不同冲击速度下的压力及温度分布Fig.7 The pressure and temperature response in material 2# at different particle velocities based on the mesoscale model with uniform particles

3.2 典型Al/Ni 多层复合材料冲击压缩细观模型计算结果

3.2.1 细观颗粒变形情况

Al/Ni 多层复合材料与Al/Ni 粉末复合材料具有完全不同的细观结构和细观尺寸，相关试验也表明两者的宏观力学行为和冲击释能特性具有较大差异［24］。基于SEM 照片建立的3#材料细观模型在典型冲击速度下的颗粒变形情况，如图8 所示。同前述计算结果，冲击压缩速度越高，细观颗粒变形越剧烈，冲击压力和温度也相应增加。其中，颗粒变形情况主要表现为两个方面：（1）Al、Ni 材料细观层在压缩加载下发生体积压缩而变薄；（2）Ni 颗粒的两端及中间初始厚度较薄区域比其他区域变形更快，从而出现类似于流体的流动现象，使其细观颗粒更加弯曲甚至断裂。

图9 为厚度比为0.32/0.2 且各细观层保持轧制之前初始形态的3#材料均匀化细观模型计算结果，该结果与基于真实细观结构的细观模型计算结果存在较大差异。对于Al、Ni 细观层，在冲击压缩过程中主要发生了体积压缩，而无明显变形现象。

图8 基于SEM 的3#材料在不同冲击压缩速度下的变形情况Fig.8 The deformation of layers in material 3# at different particle velocities based on the mesoscale modelwith SEM images

图9 3#材料均匀化细观模型在不同冲击压缩速度下的变形情况Fig.9 The deformation of layers in material 3# at different particle velocities based on the mesoscale model with uniform layers

3.2.2 冲击压力及温度计算结果

图10 为不同冲击条件下基于SEM 照片建立的3#材料中压力和温度响应计算结果。与2#材料相比，3#材料在冲击压缩过程中的压力和温度分布更加不均匀，且其分布情况均与材料的颗粒分布情况相关。从图10 中压力云图可以看出，3#材料的冲击波波阵面形状为与波阵面处颗粒形状相似的曲面。此外，从温度分布云图可以看出，Al 相的冲击温度显著高于Ni 相，这是由于Al 的可压缩性比Ni 好。当冲击速度Up=300 m·s-1时，该材料内最高冲击压力为8.8 GPa，最高冲击温度为472 K。随着Up提高至1200 m·s-1，冲击压力和冲击温度最大值分别升高至72 GPa 和2856 K。由此看出，3#材料内的冲击温度和冲击压力高于2#材料。

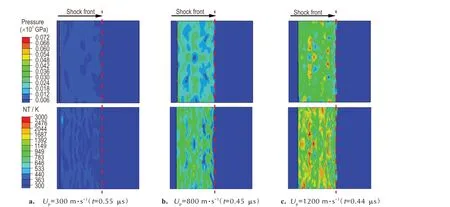
图10 基于SEM 的3#材料细观模型在不同冲击速度下的压力及温度分布Fig.10 The pressure and temperature response in material 3# at different particle velocities based on the mesoscale model with SEM images

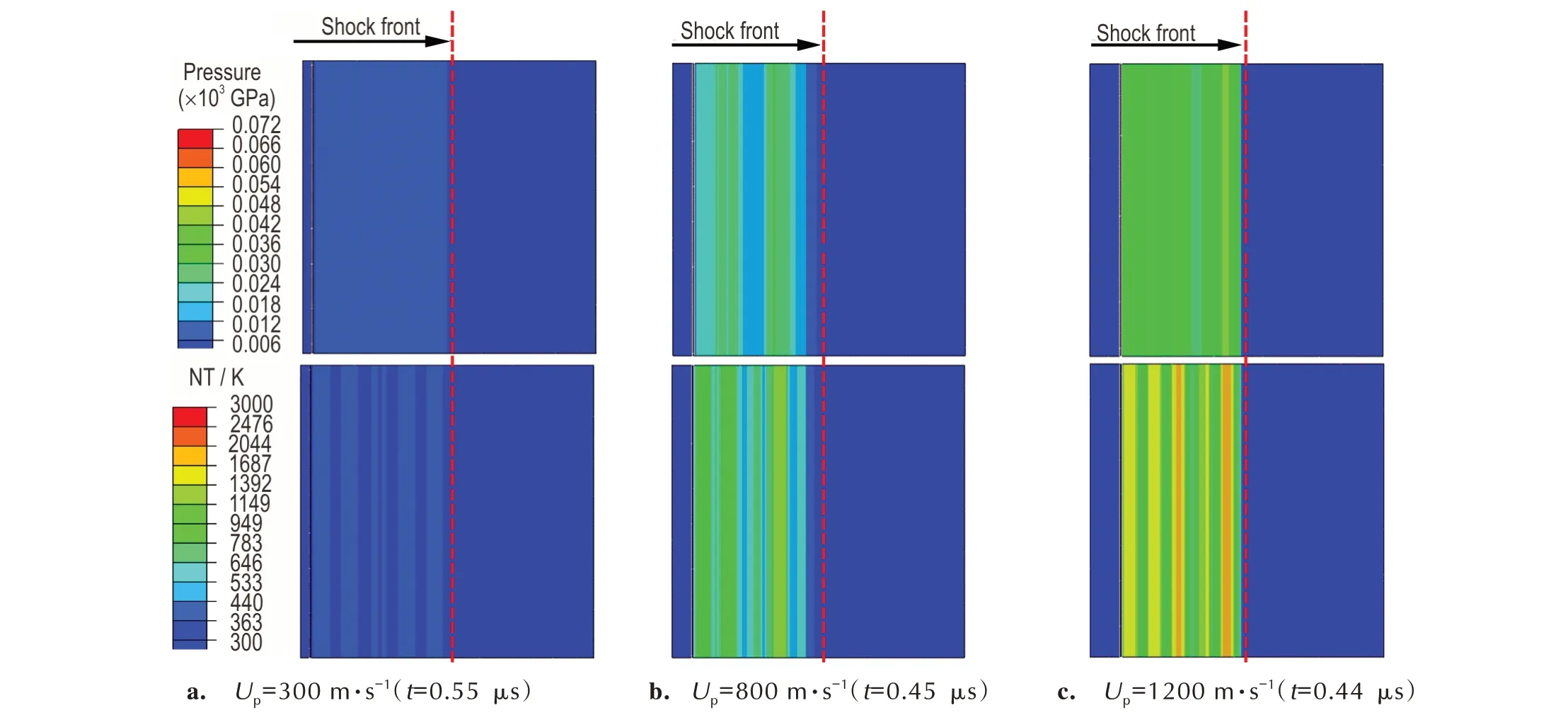
图11 3#材料均匀化细观模型在不同冲击压缩速度下的变形情况Fig.11 The pressure and temperature response in material 3# at different particle velocities based on the mesoscale model with uniform layers

图11 为3#材料均匀化细观模型冲击压力和温度计算结果。计算结果表明，基于该细观模型得到的材料内冲击波波阵面为与材料细观层完全平行的平面，温度分布云图为与Al、Ni 材料位置相关的高、低温间隔且平行分布的结构。此外，由于细观层结构规则且均匀分布，该细观模型的计算结果中无局部高温、高压点。因此，基于初始细观形态建立的3#材料细观模型无法预测冲击压缩局部高压和热点结果。

3.3 Al/Ni类含能结构材料的冲击Hugoniot参数计算

图12 基于两种细观建模方法的Al/Ni 类含能结构材料Us-Up关系计算结果对比Fig.12 Comparison of the Us-Up relationship of Al/Ni materials calculated from two modelling methods

表3 三种Al/Ni 类含能结构材料状态方程参数计算结果Table 3 The calculated Hugoniot parameters of three Al/Ni composites

根据前述冲击波参数的计算方法，得到了三种Al/Ni 类含能结构材料在不同冲击压缩速度Up下产生的冲击波速度Us。对离散的Us-Up数据点进行线性拟合得到了Hugoniot 参数，结果如图12 和表3 所示。对于1#材料，两种建模方法得到的计算结果无明显差异。而对比2#材料两种细观模型计算结果可以发现，基于SEM 照片建立的细观模型计算得到声速和冲击波速度均高于细观颗粒形状均匀的细观模型计算结果。这主要是由于2#材料中的Al 颗粒含量高于1#材料，同时SEM 照片也表明2#材料细观结构中的Al 颗粒团聚现象相比于1#材料更为显著，因此采用均匀化建模方法得到的细观模型不能准确体现材料颗粒的分布情况。该结果表明，在材料细观结构中，若颗粒分布较为离散，两种建模方法计算的宏观状态方程参数结果相近；若某一颗粒含量较高而在细观结构中出现大面积的团聚现象，应优先采用SEM 照片生成的细观模型。另外，对于3#材料，基于SEM 照片建立的细观模型计算得到的材料声速低于细观层均匀化的模型计算结果，而基于SEM 照片建立的细观模型得到的材料参数S高于细观层均匀化的模型计算结果。结合前述分析可知，细观结构均匀化建模方法不适用于描述Al/Ni 多层复合材料的冲击响应行为。