基于性能退化的失效阈值变化速率对产品可靠性的影响
2020-10-31王新刚马瑞敏黄小凯常苗鑫
王新刚,马瑞敏,黄小凯,常苗鑫
(1. 东北大学 机械动力学与可靠性研究中心,秦皇岛 066004; 2. 北京卫星环境工程研究所,北京 100094)
0 引言
科学技术的进步和生产技术的发展使产品的可靠性不断提高,在允许的时间内,很难获得产品性能研究所需的失效数据[1]。性能退化分析作为一种有效弥补机械产品失效数据不足的方法,可以间接预测产品的寿命[2]。
基于机械产品性能退化的可靠度分析,关键在于产品退化模型的建立以及失效标准即失效阈值的确定。通常采用退化轨迹和随机冲击过程这2 种方法来描述机械产品的性能退化过程。退化轨迹模型是指采用一些应用较为成熟的数学模型来拟合产品性能退化量和时间的关系[3-4]。一般情况下产品的失效往往是由多种失效模式导致的,当突发失效或性能退化失效之一达到其失效阈值都会导致产品的失效[5]。Li 等[6]分析了产品同时包含随机冲击过程与性能退化过程且两者相互独立下的可靠性。Wang 等[7]考虑了外部冲击载荷对退化过程的影响,并在模糊退化数据下进行了退化分析,建立了基于模糊退化数据的可靠性模型。刘晓娟等[8]在外部冲击过程和内部性能退化过程同时存在的情况下,采用时变copula 函数建立多个退化过程和冲击过程下的竞争失效可靠性模型,研究表明产品在工作过程中,其自身的性能退化过程和所受到的外部冲击过程相互影响。An 等[9]分析了冲击载荷引起的性能退化增量与冲击载荷大小之间的关系,研究表明系统有抵抗微小载荷的能力,只有超过一定范围的冲击载荷才会对系统的性能退化量产生影响。Rafiee 等[10]在假定性能退化过程为线性的前提下,研究了外界冲击分别为极值冲击和运行冲击等情况下对线性退化速率的影响。黄文平等[11]认为突发失效的失效阈值是变化的,在极值冲击过程和线性退化过程同时存在以及突发失效的阈值受到性能退化过程影响的前提下,建立了微引擎在变失效阈值下的竞争失效可靠度模型。
在上述分析的基础上,考虑到产品本身的复杂性和工作环境的不稳定性,失效阈值为固定值不符合实际情况。随着性能退化量的逐渐增大,产品抵抗外载荷冲击的能力会逐渐减弱,即突发失效的失效阈值为随时间推移而降低的变量。温度等因素也会对材料的物理性能产生影响,因此性能退化过程的失效阈值亦为随时间推移而降低的变量。本文提出了在冲击载荷分别为极值冲击和运行冲击时,多个失效模式下的时变失效阈值可靠度模型,分析了性能退化模型和突发失效模型,建立了极值冲击和运行冲击下产品的可靠度模型,最后结合实例对所提出的模型进行了验证。
1 性能退化失效模型
如图1 所示,失效阈值随着时间推移逐渐降低,在工作应力的作用下,机械产品的性能退化量会随着工作的进行逐渐增加,在机械产品遭受外界冲击的时候(t1、 t2、 t3分别表示外界冲击载荷作用的时刻),如果外界冲击不能使得产品立即失效,就会造成产品性能退化量突然增加[12]。外界随机冲击载荷造成的产品性能退化量的突然增加和产品自身的性能退化量之和构成了产品总的性能退化量[13]。当总的性能退化量超过失效阈值H 的时候,产品便会退化失效。

图1 性能退化失效过程Fig.1 Failure process of performance degradation
为了研究方便,令产品的失效阈值变化过程和性能退化过程都服从线性轨迹模型:
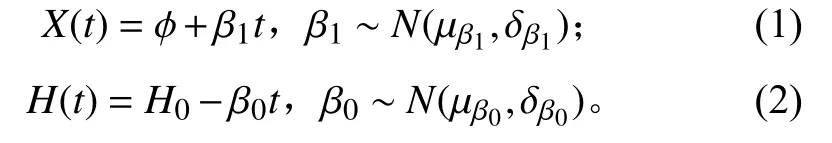
式中:X(t)为t 时刻产品自身的性能退化量; ϕ为产品的性能退化量在0 时刻的数值;β1为产品的性能退化速率,并且服从正态分布;H(t)为t 时刻产品的失效阈值;H0为0 时刻产品的失效阈值;β0为失效阈值的变化速率,且服从正态分布。


总的性能退化量为

产品在时间t 内不发生失效的概率为

2 突发失效模型
如图2 所示,用wi表示外界冲击载荷的幅值,D(t)表示突发失效阈值,外界冲击载荷的幅值服从正态分布,发生率服从泊松分布。

图2 突发失效过程Fig.2 Suddenly-occurred failure process
产品的性能退化过程会影响突发失效阈值的变化过程:随着性能退化量的不断增加,产品抵抗外界冲击载荷的能力减弱,即产品的突发失效阈值逐渐降低,当外界冲击载荷超过失效阈值时,产品发生突发失效。突发失效阈值的变化情况同样适用于其他模型。为了研究方便,假设突发失效的阈值变化服从二阶段的线性变化过程,即在产品性能退化量小于L 时以β2的速率递减,在产品性能退化量大于L 时以β3的速率递减,β2与β3均为服从正态分布函数的变量。
在时间t 内,突发失效的阈值变化情况如图2所示。设在u 时刻性能退化量正好到达L,则在时间t 内突发失效的阈值分布函数为

3 极值冲击下产品的可靠度
在时间t 内,考虑产品的性能退化失效和突发失效2 种模式同时存在的条件下,产品的可靠度可以表示为

式中:R(t|N(t) = i)为t 时刻发生i 次冲击下产品的可靠度;P(N(t) = i)为时间t 内外界冲击载荷发生i 次的概率。
R(t)的计算较为复杂,为了分析方便分以下3 种情况讨论:
1)在时间t 内,产品只发生了性能退化,则其可靠度为

2)在时间t 内,总的性能退化量小于L 且有外界冲击载荷作用于产品,则产品可靠度为

3)在时间t 内,总的性能退化量大于L 且小于H,且有外界冲击载荷作用于产品,则产品可靠度为

为了分析方便需要假定几个参数,把性能退化量刚好到达L 的时刻记为u,时间t 内的冲击次数记为i,在时间u 内冲击的次数记为k,那么[u, t]区间内的冲击次数为(i - k)。在时间u 内,把性能退化量小于L 且外界冲击次数为k 次条件下产品不发生性能退化失效的概率函数记为FX(k, x, u),则
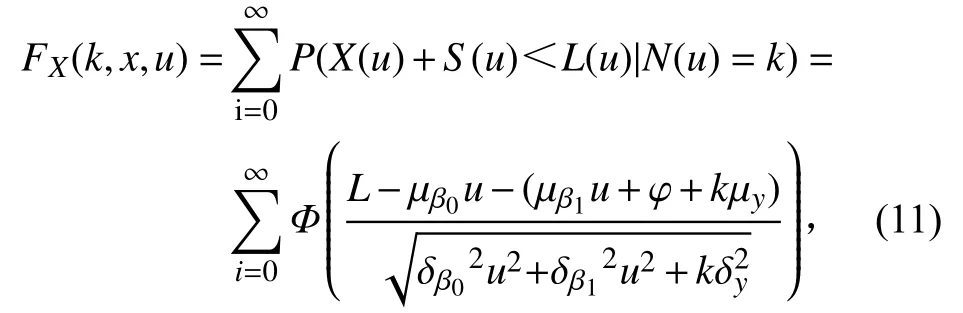
产品在时间t 内的可靠度为

机械产品在外界冲击载荷为极值冲击的前提下,在工作时间t 内其工作状态是上述3 种情况之一,因此时间t 内产品的可靠度为

4 运行冲击下产品的可靠度
如图3 所示,在运行冲击模型中,如果有连续m 个外载荷大于某个固定阈值D2或者大于突发失效阈值D(t)的时候,就会发生运行冲击失效[14]。

图3 运行冲击模型Fig.3 Operation shock model
为了分析方便首先定义Ui为在i 次外界冲击载荷中不会有连续m 个冲击载荷大于某个固定阈值D2的概率,Ui应该满足

式中:P 为冲击载荷大于固定阈值D2并且小于失效阈值D1的概率;Q 为冲击载荷小于固定阈值D2的概率。P、Q 的表达式分别为:

分3 种情况考虑产品在时间t 内的可靠度:
1)在时间t 内,产品只发生了性能退化,则其可靠度为
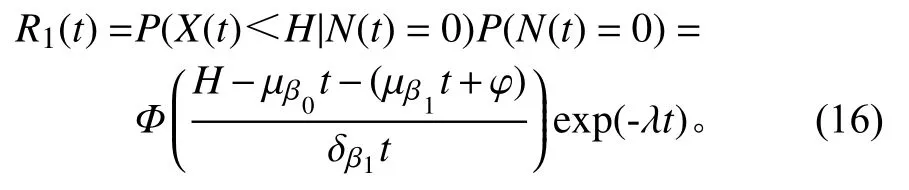
2)在时间t 内,总的性能退化量小于L 且有外界冲击载荷作用于产品,则产品可靠度为

3)在时间t 内,总的性能退化量大于L 且小于H,且有外界冲击载荷作用于产品,则产品可靠度为
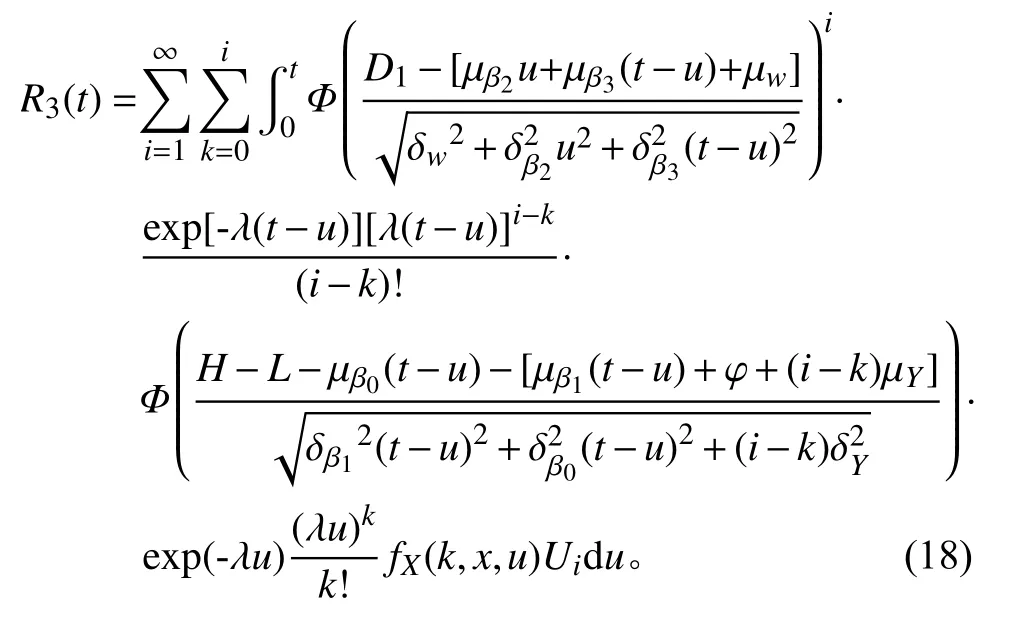
综合以上3 种情况,产品在时刻t 的可靠度为

5 实例分析
根据美国Sandia 国家实验室进行的一项实验研究发现,一种包括正交梳状驱动执行机构和相互机械连接的旋转齿的微型发动机,其梳齿传动的线性位移通过销传递到齿轮上。微引擎参数如表1 所示,随着工作过程的进行,齿轮与销连接的表面会有明显的磨损。产品正常工作时的载荷和外载荷的冲击导致磨损,外部冲击会导致微型发动机的零部件突然断裂,这2 个失效模式都可能导致微型发动机失效。

表1 微引擎可靠性分析参数Table 1 Parameter values for micro-engine reliability analysis
5.1 基于极值冲击的产品可靠性分析
产品在极值冲击的工作环境下,将表1 中的数据代入式(13),得到微引擎的可靠度函数,如图4和图5 所示。

图4 极值冲击情况下不同失效阈值变化速率下的产品可靠度Fig.4 Product reliability at different failure threshold degradation rates in extreme operation shock
根据式(13)可知,突发失效阈值的变化速率µβ2和 µβ3都对产品可靠度有影响。为了便于分析,分别给出了3 组数据。通过图4 可以看到:不考虑突发失效阈值的变化,产品的可靠度会被高估;当失效阈值变化速率变大时,可靠度曲线向左偏移,说明在一定范围内随着突发失效阈值变化速率的增大,产品的可靠度降低。
根据上文分析可以得知,当性能退化量达到L 时,产品抵抗冲击能力减弱,即突发失效阈值变化速率发生改变。在其他参数和工作时间不变的情况下,通过改变L 的大小来研究其对产品可靠度的影响。图5 分别给出了3 组不同的L 值,可以看到:在一定范围内随着L 的逐渐变大,产品的可靠度也随之提高。这是因为L 越小,突发失效阈值变化速率增大的条件越容易被满足。

图5 极值冲击情况下不同L 值下的产品可靠度Fig.5 Product reliability for different values of L in extreme operation shock
5.2 基于运行冲击的产品可靠性分析
在外界冲击为运行冲击的情况下,将表1 中的数据代入式(19),得到微引擎的可靠度函数,如图6和图7 所示。

图6 运行冲击情况下不同失效阈值变化速率下的产品可靠度Fig.6 Product reliability at different failure threshold degradation rates in operation shock
失效阈值变化速率对运行冲击模型可靠度的影响与对极值冲击模型可靠度的影响相似。在其他参数不变的条件下,给出了3 种失效阈值的变化速率。通过图6 可以看到,在一定范围内,随着失效阈值变化速率的增加,产品的可靠度降低。
数值L 对运行冲击模型可靠度的影响与对极值冲击模型可靠度的影响相似。在其他参数不变的条件下,给出了3 组不同的L 值。通过图7 可以看到,在一定范围内随着L 变大,产品的可靠度提高。

图7 运行冲击情况下不同L 值下的产品可靠度Fig.7 Product reliability for different values of L in operation shock
6 结论
本文研究了在外界冲击为极值冲击和运行冲击的情况下,突发失效与性能退化同时存在下机械产品失效阈值变化速率对产品可靠度的影响。
结果表明:1)忽略机械产品突发失效阈值的变化,机械产品的可靠度会被高估;2)突发失效阈值的变化速率会影响机械产品的可靠度,在一定范围内,随着变化速率的逐渐增大,机械产品的可靠度逐渐下降;3)决定失效阈值变化速率的性能退化量L 对产品可靠度有影响。在一定范围内,随着性能退化量L 变大,产品的可靠度提高。
