矩形钢管混凝土柱贯通隔板弱轴方向传力研究
2020-10-30费建伟李志安杨红亮刘飞东曹本富孙忠伟
费建伟,李志安,杨红亮,刘飞东,王 群,曹本富,孙忠伟
(浙江中南建设集团钢结构有限公司,浙江 杭州 310052)
矩形钢管混凝土柱是指在矩形钢管中填充混凝土且钢管及其核心混凝土能共同承受外荷载作用的竖向承重构件[1],它具有强度高、刚度大、延性好和耗能能力强、制作和施工方便、经济效果好等诸多优点[2-3]。矩形钢管混凝土结构在高层及超高层建筑中具有很好的应用前景,现已受到国内外工程领域的普遍重视[4]。在多高层建筑中,矩形钢管混凝土柱通过节点与梁等水平构件连接组成抵御地震作用的抗侧力体系,所以钢管混凝土节点的计算方法和构造措施是应用中必须解决的关键问题[5]。
现在钢管混凝土柱刚性节点主要有内隔板节点、外隔板节点、外肋环板节点和隔板贯通节点四种节点形式。隔板贯通节点是在矩形钢管内设隔板,隔板贯通钢管壁,钢管与隔板焊接;钢梁腹板与柱管壁采用高强螺栓通过连接板连接,钢梁翼缘与外伸的内隔板焊接[6]。隔板贯通节点虽然须将钢管柱在节点处断开,增加了节点区焊缝的长度,但与内隔板节点相比,解决了管柱边长较小时隔板焊接困难问题和梁翼缘与隔板对中问题,与外隔板节点相比,解决了因隔板太大墙板安装困难问题,避免了室内角部有凸角现象[7]。但隔板贯通式节点在施工中存在浇筑不方便的问题,隔板孔径越大,钢管内混凝土越容易浇灌密实,可是过大的内孔径会削弱隔板有效受力面积,降低隔板的承载能力[8]。
因此,国内外的学者对方钢管混凝土贯通隔板节点的隔板孔做了研究。Matsui[9]对方钢管混凝土柱外隔板节点和隔板贯通节点的设计方法进行了研究,分别提出了两种节点的容许抗弯承载力计算公式,被日本建筑学会的 AIJ(1987)规程所采纳,但两种方法均忽略了钢管对节点承载力的贡献。Shim等[10]以内隔板开口尺寸等为考察的主要参数,进行了钢管混凝土柱与钢梁节点的静力及滞回性能试验研究,研究表明内隔板圆孔的开口率达到50%,试件的强度几乎不会降低。苗纪奎等[11]对方钢管混凝土隔板贯通节点进行研究,研究认为隔板厚度宜大于或等于梁翼缘厚度,建议浇筑孔径R取值范围为:a-bf≤R≤bd-bf(其中a为钢管混凝土柱的边长;bf为梁翼缘的宽度;bd为隔板的宽度)。
国内外的专家学者主要是针对方钢管混凝土隔板贯通节点孔研究较多,但对矩形钢管混凝土柱弱轴方向的隔板孔的研究却很少。然而矩形钢管混凝土柱在现在的钢结构工程中应用普遍,所以对矩形钢管混凝土弱轴方向隔板孔的研究很有必要。
1 矩形钢管混凝土柱隔板构造设计
目前规范对于钢管混凝土柱隔板设置灌浆孔都是采用居中的圆孔形式,四角部设置透气孔,不论是方管还是矩形管,都是相同开孔形式,且在规程上给出了隔板承载力计算公式,可以方便工程师应用。随着国家装配式建筑的推进,钢结构住宅也得到了发展和应用。对于钢管混凝土柱,采用矩形钢管较方管更适合居住建筑,能很好地解决露柱问题;但是伴随而来的问题是矩形管弱轴方向刚接梁节点构造问题,目前有采用竖板连接的构造方式。该连接构造将翼缘内力通过竖板进行转换,实现了节点的弯矩传递;在住宅结构中若采用外隔板节点,势必隔板露出需要包覆,影响建筑视觉感官;若采用隔板贯通节点,则传统的居中圆孔构造方式,使得孔开不大。这势必影响混凝土灌浆,因此改变了开孔方式,改为矩形孔或长圆孔形式。见图1。
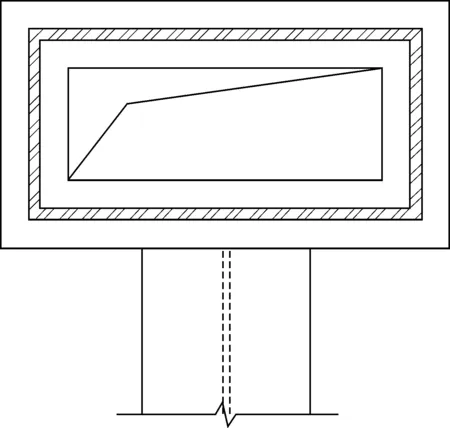
图1 隔板贯通节点
2 节点受力机理分析
隔板在钢梁翼缘的拉力作用下,假设为局部均布荷载作用,为约束梁的计算模型。隔板的约束情况比较复杂,两侧面壁板约束较强,可以认为是固端约束,正面壁板对隔板为弹性约束,两者会共同变形,因此翼缘荷载按两者的刚度进行分配。隔板的计算模型见图2,壁板的计算模型见图3。
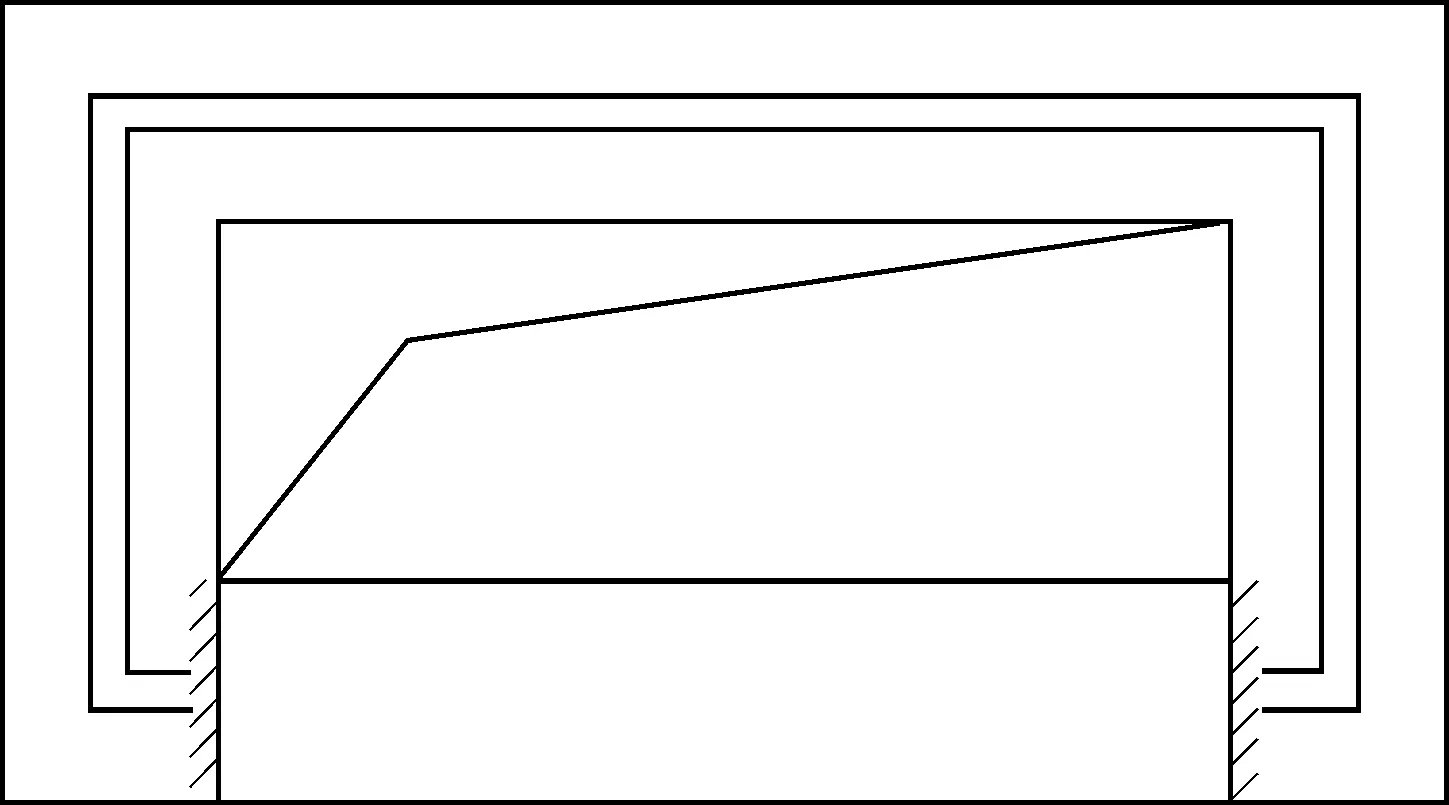
图2 隔板受力模型
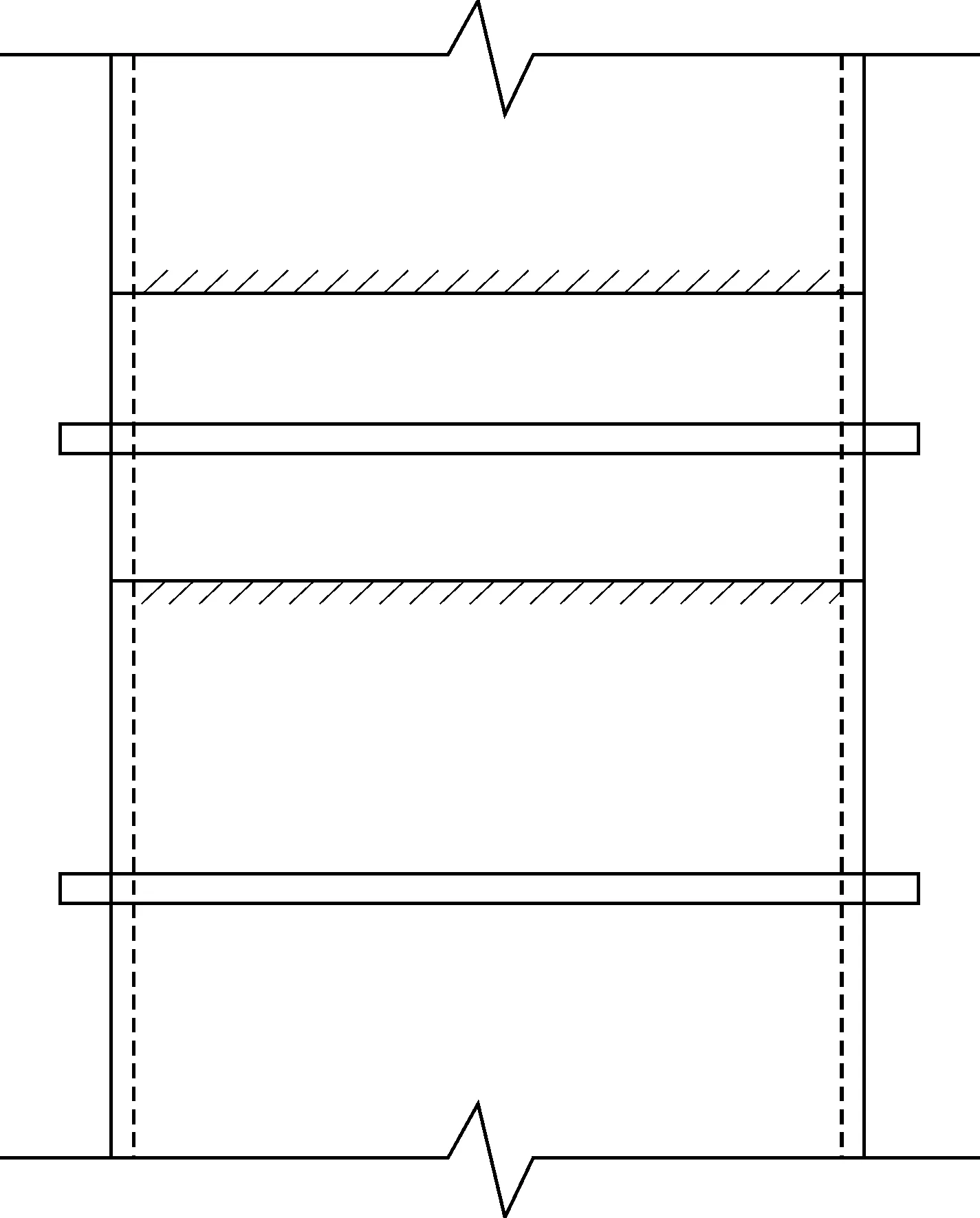
图3 壁板受力模型
取柱子截面口a×c×t,a为钢管柱截面长,c为钢管柱截面宽,t为钢管柱厚度;隔板厚度为d,外伸宽度为n,则隔板受力模型假定为两端固端梁,固端梁跨度为l,灌浆孔宽度为f,固端梁截面高度为h=(c+2n-f)/2,固端梁截面宽度即隔板厚度为d。钢梁翼缘宽度一般小于固端梁跨度,即作用在固端梁跨间局部范围。假定作用力均布分布在固端梁跨度范围,则固端梁在单位均布荷载作用下跨中挠度为v1=l4/384EI,则刚度为k1=384EI/l4,其中,I=dh3/12。
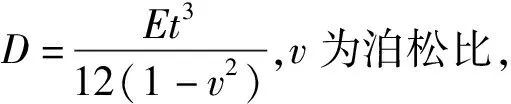
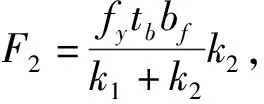
3 算 例
某矩形钢管混凝土柱的截面高a为350 mm,宽c为170 mm的扁柱,壁厚t为12 mm,弱轴方向连接钢梁,钢梁翼缘宽度bf为150 mm,厚度tf为10 mm,隔板厚度d为14 mm,壁板影响高度b为158 mm,钢材屈服强度fy为345 MPa,灌浆孔长度L为280 mm,灌浆孔宽度f为100 mm。则固端梁高度h=60 mm,固端梁惯性矩I=252 000 mm4,固端梁刚度k1=3 243 N/mm,壁板单位抗弯刚度D=32 597 802 N·mm,a/b=2.215,根据铁木辛柯《板壳理论》[12]求得m=0.002 64,则壁板刚度k2=3 129.6 N/mm,则壁板上作用的力F2=254 139 N,隔板上作用的力F1=263 360 N,则壁板上作用的线荷载q2=726.1 N/mm,隔板上作用的线荷载q1=940.6 N/mm。
将上述构件采用有限元软件进行实体建模及数值分析,有限元模型见图4。经分析得知,当翼缘达到全截面屈服状态时,隔板剪应力云图见图5。钢梁与隔板的等效应力云图分别见图6、图7。

图4 有限元模型
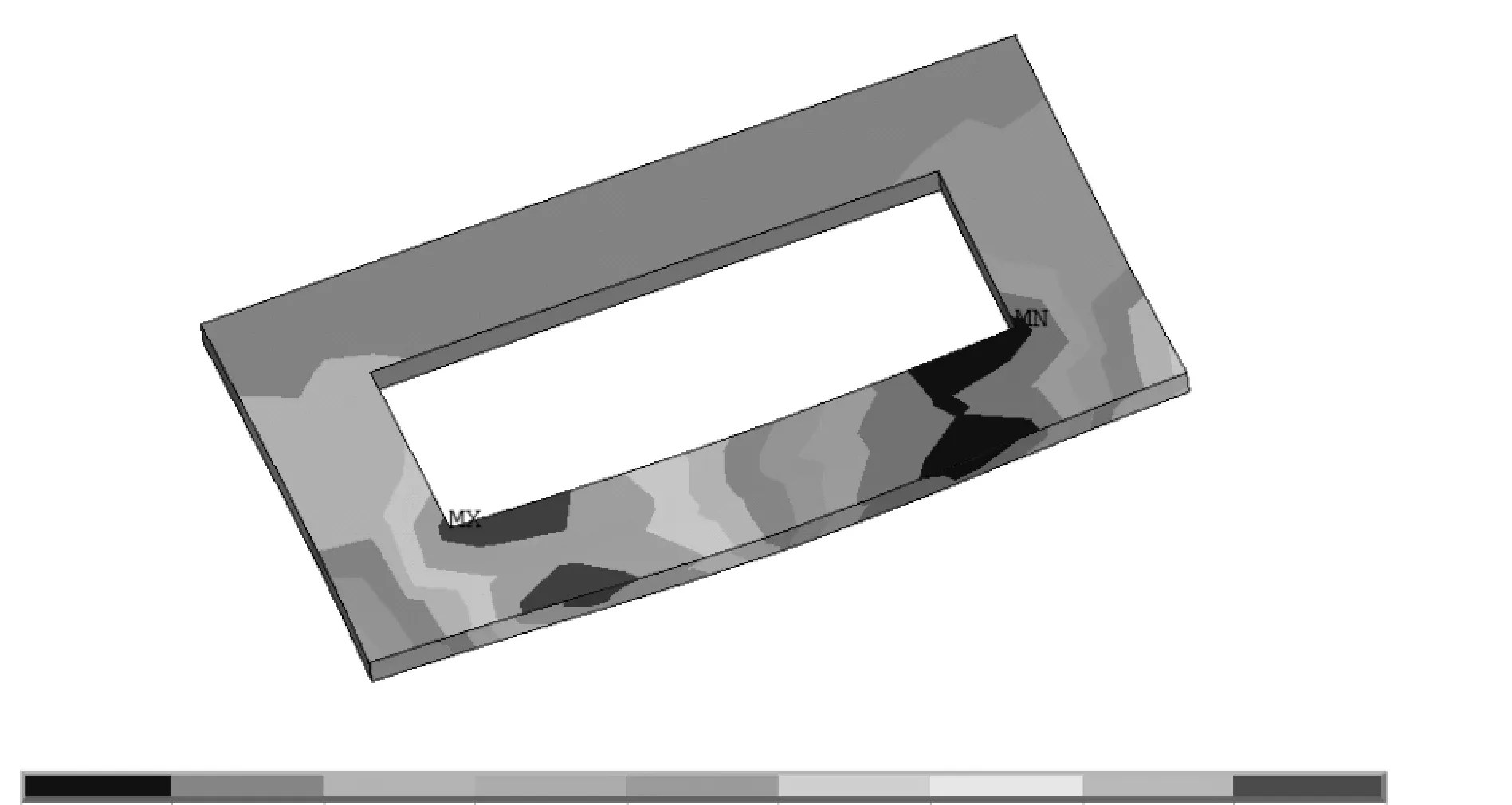
图5 隔板剪应力
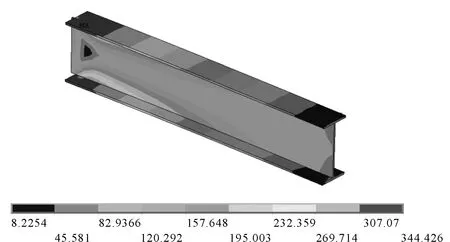
图6 钢梁等效应力

图7 隔板等效应力
从图5可知有限元模拟得到的剪应力与简化公式求得的剪应力相当,因此可采用上述公式进行隔板承载力验算;由图6与7可知,当钢梁屈服时,隔板在开孔壁上的受拉区与受压区进入屈服,也由固端梁的受力模型可以知道位于固端梁的跨中和端部。
4 结 语
对于矩形钢管混凝土柱,弱轴方向截面高度较小,隔板贯通节点能较好传递钢梁弯矩,但传统灌浆孔方式孔径较小,对于混凝土灌浆很不利。改变了传统的灌浆孔,改为矩形孔,增大了灌浆孔开孔面积,由此带来的问题是隔板承载力计算没有现成公式。通过对隔板与壁板的变形协调分析,得出了隔板的受力机理。推导相关公式,并采用有限元数值模拟进行对比验算,结果是两者吻合较好。下一步改进灌浆孔,由矩形孔改为长圆孔,是否会改善直角处的应力集中,有待进一步研究。
