多智能体系统分布式事件触发控制综述

张凯杰 王丹丹 吕跃祖

0 引言

随着计算机科学、人工智能和互联网的发展,多智能体系统(Multi-Agent Systems,MASs)受到众多研究者的关注,成为了控制学科和人工智能领域的研究热点[1-2]．MASs是由多个具有感知、通信、计算和执行能力的个体(智能体)组成的系统,智能体之间通过网络拓扑与其他智能体进行信息交互,从而协调完成较为复杂的任务．在现实应用中,智能体的通信资源、计算能力等通常是有限的,且智能体之间往往不能进行实时通信,每个智能体的控制器也无法进行实时更新．为了解决上述问题,提高线上资源的利用率,传统的处理方式是采取时间触发,即触发时刻是事先确定好的,而不是根据系统的状态或时间进行动态确定的,甚至是周期控制[3].这种方式虽然在一定程度上降低了通信及计算成本,但具有一定的局限性：一方面是当智能体的行为临近收敛状态时刻或者是在干扰较小的理想状态,如果继续使用时间触发采样控制会使得网络代价成本较高,造成不必要的资源浪费;另一方面是当时间触发中的采样周期较小,即采样频率较高时,网络中会存在大量的冗余信息,从而会导致网络堵塞,增加网络传感器的负担,甚至导致网络系统的崩塌.

事件触发是基于预先给定触发条件的一种控制方式,若控制任务满足触发条件,例如系统的状态误差超过某一设定阈值(通常与系统状态或时间有关),则事件发生,此时系统执行触发任务,进行邻居之间信息的传递或者控制器的更新．与时间触发控制相比,由于事件触发控制的采样时间取决于触发条件是否满足,因此它可以有效减少控制任务的执行次数,节约通信、计算资源,一定程度上解决了网络拥堵的问题．在分布式控制系统中,文献[4]更加清楚地描述了时间触发和事件触发的区别．在MASs分布式控制中,智能体之间进行信息交互会产生一定程度的消耗,所以采用连续时间控制会很大程度上造成通信资源的浪费．由于事件触发控制在节约通信、计算等资源方面的优势,其在多智能体系统分布式控制中已得到广大研究者的关注,并已经被广泛地应用到各个领域[5-6].

1962年,事件触发机制率先由Dorf等[7]提出,它是一种通过测量系统参数来改变采样频率的自适应系统．随后，事件触发的思想应用于发动机控制中,用来解决传感器问题[8]．早在1999年的IFAC(国际自动控制联合会)会议上,有关事件触发的论文[9-10]一经发表就引起了科研工作者的广泛关注,文献[9-10]说明了与时间触发控制相比,事件触发控制具有的一些优势．2002年,CDC(IEEE决策和控制会议)会议上Aström等[11]通过对比事件触发采样和周期采样的区别,得到了事件触发采样的效果更好的结论．随着越来越多研究者对事件触发控制研究的关注,而后的CDC会议上针对事件触发还设置了专题分会,这在一定程度上反映了事件触发控制在多智能体系统中的重要性．与此同时,在人工智能飞速发展的浪潮下,智能体之间的通信成为了关键的传递信息的方式,它是维持多智能体系统保持协同一致以及追踪的重要基础,在这样的背景之下,对于通信资源的整合和利用变得愈加重要.在保证系统稳定性的基础上,事件触发控制能够更好地节约通信资源,带来更大的经济效益,有着广阔的应用前景.

本文基于事件触发通信,介绍了不同状态下系统中智能体的通信情况,从时间方面分别分析了连续时间和离散时间下的触发机制；给出了基于边的事件触发、自触发控制、动态事件触发以及异步事件触发的主要内容；阐述了事件触发在MASs实现一致性、分布式优化以及博弈上的一些应用.

1 事件触发通信机制

本节主要从时间的角度介绍事件触发的不同通信方式,包括连续时间下的事件触发控制和离散时间下的事件触发控制．在多智能体系统中,当智能体状态满足事件触发条件时,它需要向其他智能体传递自身的状态使得控制策略更新,进而执行相对应的任务,但是如何与其他智能体进行通信,这是一个关键性的问题.

1.1 事件触发控制

1.1.1 连续时间通信

连续事件触发需要硬件连续对智能体的状态进行检测判断触发条件是否满足,连续时间状态下事件触发的运行机制如图1所示.在连续时间触发控制中,检测器会对智能体的状态进行实时的检测,当触发条件满足时才进行信息的传输.

图1说明对于一阶系统[12]

(1)

(2)

(3)

xi(t),vi(t),ui(t)分别代表智能体i的位置、速度和控制输入．为了便于分析,文献[13]中设置了两种状态误差:

(4)

它所对应的事件触发控制为

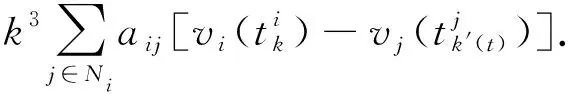
(5)

然后利用稳定性定理进行分析证明,得到系统的状态是收敛的．对于一般线性系统

(6)

文献[14]为了实现领导者和追随者的状态一致,基于事件触发机制设计控制协议如下:

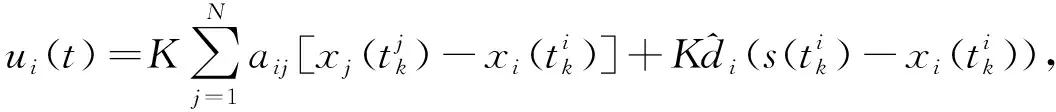
(7)

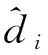
1.1.2 离散时间通信

与连续通信相对应的就是离散通信．不同于连续时间下的事件触发控制,离散时间下的事件触发是以周期进行采样的,也可称为周期事件触发．周期事件触发最早是由Heemels等[16]提出的,其触发原理流程如图2所示.

与连续时间触发不同,图2周期事件触发控制是基于周期采样器,周期性地对事件触发条件进行检测,当系统触发时智能体将采样状态进行传输．周期事件触发是一种结合了周期采样和事件触发的控制机制,由于它是周期性地对事件触发条件进行检测,任意两次触发的时间之间一定存在一个正的下界,因此这种触发是不存在Zeno行为的．周期事件触发实质上是连续事件触发的离散化,在实际应用中连续的检测需要耗费一定的资源,因此周期事件触发在系统控制中的应用更加广泛．周期事件触发以时间间隔h进行采样,可由下面算法来判断是否进行传输:

[x((k+j)h-x(kh))]TΦ[x((k+j)h-x(kh))]≤ηxT((k+j)h)Φx((k+j)h),

(8)

其中Φ是一个对称正定的矩阵,η∈[0,1),j=1,2,….

需要注意的是,若采样状态x(k+j)h满足上述不等式(8)将不会被传输,只有超过上述不等式的阈值时,采样状态才会被发送到控制器．由于周期事件触发的一些优良特质,它被应用于很多方面．在一类由高维主系统和低维从系统构成的主从耦合系统中,文献[17]设计了一种事件触发的采样数据传输策略．在线性系统中,文献[18]研究了基于观测器的控制,并提出了一种新的事件触发机制,这种机制可以减少传感器到控制器通道和控制器到执行器通道的通信．对于线性定常系统,文献[19]提出了基于周期事件触发的滑模控制设计的方法,这种触发机制在智能体状态可测的那些瞬间进行周期性评估,不再需要连续判断事件触发策略,实现起来更具有经济价值.

1.2 基于边的通信

对于事件触发控制,可以根据事件触发条件设计的对象将其分为基于边的事件触发机制和基于点的事件触发机制.基于边的事件触发建立在智能体之间的连边上,当事件触发条件满足时,连边上的智能体之间进行信息交互．而基于点的事件触发针对的是系统中的每个智能体,触发条件满足时智能体会与它所有的邻居进行信息交互,上述相关设计都是基于点的.

(9)

当k属于触发时间集合时,智能体i通过连边向智能体j传递它此时的状态,否则智能体j保持上一时刻智能体i对其传输的状态,事件触发条件如下:

(10)

其中eij(k)是可调节的阈值．阈值和事件触发的次数相关,阈值越小,触发次数越多,意味着智能体之间的通信越频繁．文献[20]研究基于边的事件触发机制下的网络系统的协调问题．对于一般线性MASs的编队控制问题,文献[21]提出了四种基于边的事件触发控制协议,且每种协议都不存在Zeno行为.

1.3 自触发控制

由于事件触发需要专门的硬件设施去实时监测系统的状态,当系统的状态误差满足触发条件时,事件发生．正常的操作系统中,事件触发机制是可以满足的,但是在一些大规模或者比较极端的情况下,使用事件触发机制可能会造成一些资源的浪费．与事件触发相比,自触发是主动的一种通信方式,它可以提前根据上一触发时刻的数据计算得到下一个触发时刻,其原理如图3所示.

图3自触发控制通过当前的采样值和采样时刻来决定下一时刻的触发,通过这种机制直接进行采样状态的传输．基于自触发机制,下一个触发时刻通过下述公式确定:

tk+1=tk+τk,

(11)

其中τk=Γ(x(tk)),Γ是x(t)在tk时刻的函数．自触发控制是Velasco等在实时系统中提出的一个概念[22],它和事件触发控制有着一定的区别,主要体现在通信方式上,具体详细阐述可参考文献[23-24]．由于自触发控制只需要当前智能体的信息状态就能够确定下一个触发时刻,因此它在分布式控制中可以得到很好的应用．文献[25]分析了自触发控制在具有一致目标的MASs中的应用．文献[26]抛弃了传统反馈控制律上的周期性的假设,通过自触发机制利用被测对象的当前状态来决定下一个被测状态、计算控制律和更新执行器的时刻．文献[27]基于自触发提出了一种协调算法,分析了在同步和异步情况下算法的正确性.

1.4 动态事件触发

静态事件触发的触发条件中只有智能体的状态项和误差项,为了更好地对Zeno行为进行分析,同时减少触发次数,通过引入动态变量η,文献[28]提出了如下动态事件触发机制:

(12)

(13)

其中βi>0,ξi∈[0,1],内部动态变量的初值ηi(0)>0．需要注意的是,触发条件中的θi是后期待定的参数,当θi趋于无穷时,式(12)就对应于静态事件触发条件,静态事件触发实质上是动态事件触发的特例．文献[29]通过引入动态变量证得闭环系统的稳定性．文献[30]的动态事件触发控制策略同时保证了干扰到输出的有限Lp增益和事件触发时间的严格正的下界.

1.5 异步事件触发

事件触发根据每个智能体是否同时触发还可以分为同步事件触发和异步事件触发．在控制系统中,如果事件触发条件是针对所有的智能体,当满足触发条件时,所有的智能体都进行信息的传输和策略的更新,这种触发控制称为同步事件触发,对于每个智能体而言该触发通信是同步的．但是在一些实际情况中,同步更新并不一定能够实现,因为它需要用到系统中所有智能体的状态信息来判断触发条件是否满足,而且可能造成不必要的资源浪费,这时需要对智能体单独设计事件触发条件,使得智能体的更新并不是同步的,即每个智能体都有自己的事件触发时刻序列,此为异步事件触发．在具有完全状态反馈的非线性系统中,文献[31]提出了一种分布式的异步事件触发方法,利用局部信息来确定从传感器到中央控制器的传输时间,所提出的方法不仅保证了系统的稳定性,也使得采样的时间具有正下界,排除了Zeno现象．文献[32]针对一组不在同一位置的传感器,设计了分布式事件触发控制器,其中传感器不需要同步测量的采样方式．在输出测量和控制输入受到噪声干扰的系统中,文献[33]根据控制器和被控系统的动态输出分别设计了事件触发条件.

2 事件触发的应用

事件触发控制在保证了底层需要的同时,减少了智能体之间的通信频率．一些研究人员已经分析了它在各个领域的作用,比如在解决滤波问题[34]、网络电力系统[35]以及在时延控制系统[36]中．下面简要分析事件触发在MASs一致性、分布式优化以及博弈方面的应用.

2.1 MASs一致性问题

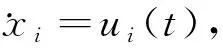
fi(ei(t))≤Δi(zi(t)),

(14)

当智能体的状态不满足事件触发条件时,智能体与其邻居之间进行通信,引发控制一致性协议更新,最终在事件触发一致性控制下达到协同状态．在一般线性动力学的多智能体系统的一致性问题上,文献[38]利用事件触发控制和自适应控制技术,提出了一种基于观测器输出反馈的分布式事件触发控制策略．对于具有时变通信延迟的线性多智能体系统的事件触发一致性问题,文献[39]提出了一种新的控制器去解决．上述研究是针对线性系统下的分布式事件触发一致性控制,其中单积分器和双积分器可以当作它的特殊情况．文献[40]对多智能体系统的事件触发一致性控制进行了详细的综述．上述多数研究内容中,在确定系统相关参数时往往需要知道系统的全局信息,如系统通信拓扑结构的拉普拉斯矩阵的特征值或其范数等,从某种意义上来说并不是完全分布式的．为了解决上述问题,研究者就结合自适应控制,提出了一种完全分布式的自适应事件触发控制协议,如文献[41]中的基于事件触发的自适应协议是完全分布的和可扩展的,它不依赖于网络图的任何全局信息,解决了无领导和领导-追随者一致性问题．文献[42]提出了一种完全分布式事件触发控制策略,对于任意连通的无向通信图,在完全分布的情况下都能解决一致性问题．针对具有通信时延和无通信时延的单积分器和双积分器网络情况,文献[43]提出的事件触发控制策略能保证智能体的行为平均一致收敛或者一致收敛到状态平均值的邻域范围内．文献[44]在无向图上提出了基于事件触发控制策略的一致性协议,该协议中的每个智能体都实现了与邻居的解耦.

2.2 分布式优化问题

优化与事件触发结合主要体现在求解目标函数的最优值,研究较多的是凸优化问题.文献[45]针对二次凸优化问题:

(15)

为了解决式(15)的凸优化问题,基于事件触发机制提出了分布式优化算法:

(16)

ki是一个常数,通过上述策略进行智能体状态的更新,最终得到优化的目的．该算法是在无向连通图的通信拓扑下进行更新的,它也可以推广到有向图和切换拓扑中．对于类似的分布式凸优化问题,文献[46]提出了一种事件触发零梯度和的算法,该算法的通信过程是由节点监控的触发条件所驱动的,在连续时间下基于采样进行监控,离散时间下则使用所提出的算法,并且证明了此算法是指数收敛的．文献[47]基于事件触发通信,给出了一种步长恒定的分布式优化算法,并且利用小增益定理证明了收敛性．文献[48]通过异步事件触发方案,解决了多个智能体最优化自身的目标函数的问题,并且在忽略通信延迟的情况下可以保证系统的收敛性．对于带有约束的优化问题,文献[49]提出了一种基于事件触发通信的分布式次梯度方法,在该方法中,所有代理的状态在步长递减和可加性条件以及触发条件的阈值下渐近收敛于一个最优解．在连续时间动力学系统中,文献[50]通过对系统设置事件触发条件使得智能体的状态渐近收敛到全局的最优解．在二阶多智能体的凸优化问题中,文献[51]将事件触发和时间触发算法相结合,使智能体协同收敛于优化问题的最优解．同样在二阶连续时间系统中,文献[52]通过一种基于事件触发的完全分布式优化算法,证明了该系统的指数收敛性.

2.3 博弈问题

在一场博弈中,每个智能体都趋于使得自己的利益最大化或者成本最小化,将事件触发机制引入到博弈中也是一种很好的应用．在N个智能体下的聚合博弈中[53],每个博弈者i的目标是解决如下的优化问题:

(17)

3 稳定性分析

稳定性一直是系统研究的重要问题．在控制系统中稳定性能够保证智能体的状态是收敛的,这在实际生活中有着重要的意义．因此在事件触发控制中,触发条件的设计必须保证系统的稳定性.

3.1 李雅普诺夫稳定性

在现代控制理论中,一般采用李雅普诺夫稳定性(Lyapunov stability)去判断该系统的特性．在事件触发通信过程中,依旧可以通过构造李雅普诺夫候选函数,根据稳定性定理证得智能体的状态是收敛的．对于带有时滞的控制系统[55],需要构造Lyapunov泛函去证明系统的稳定性.

3.2 输入状态稳定性

可以利用输入状态稳定性(input-to-state-stability)去分析系统的性能.文献[56]研究了具有有界扰动的事件触发控制系统,给出了具有观测器输出反馈的输入状态稳定性的结果.

4 Zeno行为分析

Zeno行为是指在事件触发控制中,在有限时间内发生无限次触发的现象,这种情况在物理上是不可实现的,在现实中也是不合理的．Zeno行为存在与否与事件触发条件的设置有关,通常事件触发条件的设置会保证两次触发的间隔有一个正的下界．对于周期事件触发而言,由于其采样的数据是周期性的,这种采样是离散的,任意两次采样的时间间隔一定会大于一个正值,所以已经避免了Zeno行为,但是对于其他方式的触发,需要分析Zeno行为是否存在．目前Zeno行为的分析没有特定的方法,比较常见的方法如下.

4.1 正下界法

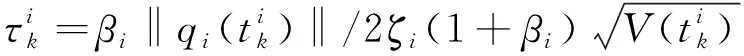
4.2 反证法

5 总结与展望

事件触发控制策略,由于它自身具有很多优良的特点,可以尽可能地实现资源的优化,节省成本,在现实生活中发挥着重要的作用．越来越多的科研工作者对事件触发控制进行研究．本文首先从时间方面分析了连续时间和离散时间系统下的事件触发机制,又介绍了几种常见的事件触发控制,例如自触发控制、基于边的事件触发控制、动态事件触发控制以及异步事件触发控制．然后分析了其在MASs一致性问题、分布式优化以及博弈问题中的相关研究进展.

虽然,关于事件触发控制方面的研究已经取得了很多不错的成果,但依然存在很多问题需要去解决．本文对于事件触发控制的进一步研究做出了如下展望:

1)目前分析Zeno行为的方法较少,没有一套成熟的、可普遍适用的理论框架．一般情况下还是使用任意两次触发之间间隔的正下界性和反证法,对于其他的证明方法有待进一步探究.

2)对于误差状态小于阈值的触发条件来说,阈值的大小决定了事件触发的频率,阈值越大,触发次数越少,可以更大程度地减少通信频率,但系统的收敛速率就会相对较慢.所以如何更好地设计误差触发条件,在保证收敛性能的同时使得通信频率也较少,这一问题值得更深层次的研究.

3)现阶段的事件触发分析是基于控制器已经设定好的情况下,如何设计事件触发条件和控制器结合起来的控制机制需要更多的科研工作者进行研究.

4)在离散时间下，设计事件触发条件时如何使用内部动态变量,这个问题有待解决.