基于模拟退火算法的无人机山地作业能耗最优路径规划
2020-10-29范叶满沈楷程翟长远张海辉
范叶满 沈楷程 王 东 翟长远 张海辉
(1.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100; 2.农业农村部农业物联网重点实验室, 陕西杨凌 712100;3.北京农业智能装备技术研究中心, 北京 100097)
0 引言
随着无人机技术的发展,农业航空越来越受到关注[1-2]。目前无人机已广泛应用于作物遥感、农情监测、农业植保等领域[3-6]。对于植保作业来说,其最大限制因素是无人机的有效续航时间[7-8]。现阶段无人机作业控制方式多为人为遥控,作业时对操作员的要求较高[9-10]。进行合理的作业路径规划可有效提高无人机的续航能力,降低对操作员的技术要求,从而进一步提高无人机的作业效率和作业效果。
近年来,对于无人机的路径规划研究较多,大都集中在平原地区大田块等地势平坦、视野开阔区域的应用研究方面[11-12],且多数以返航次数最少或者有效覆盖面积最大为约束条件进行二维平面的作业路径规划。徐博等[13]研究了基于作业方向的不规则区域作业航线规划方法,该方法可根据指定作业方向对作业航线进行规划,使无人机的能量损耗和药液损耗最小。王宇等[14]运用栅格法构建环境模型,并根据作业相关信息为相应栅格赋予概率,使无人机路径优先选择概率高的栅格,以提高植保作业效率。徐博等[15]利用栅格法对无人机植保作业区域进行划分,从而快速得到往复遍历式的作业路径,通过对无人机各架次的喷药量和返航点进行合理分配,降低无人机在非作业情况下的能量消耗。徐博等[16]研究了一种植保无人机全局航线规划方法,将整个航线规划分为单个区域航线规划、区域间作业顺序规划和区域间调度航线规划3部分,并基于智能算法得到区域间的优化作业顺序和区域间的调度航线。李继宇等[17]研究了一种基于能量优化的无人机喷施规划组合算法,通过设置补给点,并合理地分配各架次的返航点和有效载荷,从而提高了作业效率。彭孝东等[18]基于自主恒速飞行和最小转弯半径约束的无人机转弯掉头策略,对农用小型无人机进行了全区域覆盖条件下的路径规划与优化,从而减少了无人机作业时的空行行程。现有无人机作业路径规划研究主要在不规则区域作业、多机协同作业和作业总架次最少等方面展开,尚未涉及无人机植保作业的三维路径规划。丘陵山地约占国土面积的70%,其地形起伏多变,田块碎小,形状各异。无人机在山地作业时需频繁起降,其能量消耗较平原地区作业大。因此,在无人机三维路径规划时需要考虑无人机自身的能量消耗情况,以无人机飞行能效为约束条件,实现无人机在丘陵山地区域的作业效率最大化。
本研究以山地果园为研究区,以回旋翼无人机为试验对象,采用模拟退火算法对无人机作业路径进行规划,以实现无人机在丘陵山地区域作业的能耗最优。
1 无人机运动模型构建与简化
1.1 无人机运动分析
对无人机进行运动受力分析,本研究使用自行搭建的四旋翼无人机为试验对象,其主要配置为:朗宇X4108s-kv380型电机;好盈Platinum-30A-Pro OPTO型电子调速器;1555型碳纤螺旋桨;Tarot 650型机架;DJI A2型飞控;其整体结构的对角电机距离为650 mm。
对于四旋翼无人机来说,4个相同规格的无刷电机和螺旋桨分布于4个机臂的末端,用于产生升力,飞行时在飞行控制器和电子调速器的共同作用下调节4个无刷电机和螺旋桨的转速,实现升力调节,从而控制无人机的飞行姿态[19]。为了构建四旋翼无人机的三维运动模型,将其基本飞行模式分为以下4种[20]:垂直运动、俯仰运动、横滚运动和偏航运动。
为了对四旋翼无人机进行基本飞行模型的受力分析,首先对无人机进行以下模型假设[21]:①将无人机视为刚体,整个机体完全均匀对称,且运动过程中不发生弹性形变。②4个螺旋桨正交安装,机体坐标系的原点与无人机的几何中心及质心重合。③无人机所受阻力和重力不受飞行高度等其它因素影响,保持为恒定值。④无人机飞行环境中无较大气流扰动,外界干扰可以忽略。
1.2 无人机运动受力模型简化
为了对无人机运动过程的受力模型进行简化,假设无人机的工作环境无风,即在分析飞行过程受力情况时不考虑外界干扰的影响。此外,无人机在山地区域超低空作业时,行间杂草和树木枝条等在不同生长期时植被高度变化较大,如无人机进行斜升或斜降飞行会存在一定的作业安全隐患。因此在简化分析过程中,对无人机的复杂运动过程不做考虑,且不考虑无人机的偏航过程,仅对无人机在空间中的三维直线运动进行分析,此时无人机的水平运动和垂直运动受力分析如图1所示。
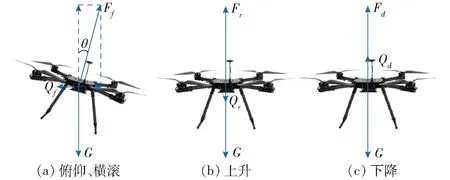
图1 无人机运动受力分析Fig.1 Force analyses of motion for UAV
图1中,Ff、Fr、Fd为无人机在不同运动状态下产生的升力,N。Qf、Qr、Qd为无人机在不同运动状态下所受的阻力,N。θ为无人机在水平运动时其升力方向与重力方向的夹角,(°)。G为无人机所受重力,N。
设重力加速度为g,无人机质量为m。当无人机以速度vf匀速直线飞行时,由于无人机进行匀速运动,无人机所受的合外力为零,由图1a可得无人机匀速直线飞行时的运动学方程为
(1)
设此时无人机的功率为Pf,可得无人机水平移动速度为vf时的能效系数Kf,即飞行过程能耗与飞行距离的比值
(2)
式中t——无人机飞行时间,s
当无人机以速度vr匀速上升时,其空气阻力Qr与其运动方向相反,对无人机的升力Fr起阻碍作用,由图1b可得无人机匀速上升飞行时的运动学方程为
Fr=Qr+mg
(3)
设此时无人机的功率为Pr,可得无人机垂直上升速度为vr时的能效系数Kr为
(4)
当无人机以速度vd匀速下降时,空气阻力Qd与其运动方向相反,对无人机的升力Fd起协助作用,由图1c可得无人机匀速下降飞行时的运动学方程为
Fd=mg-Qd
(5)
设此时无人机的功率为Pd,可得无人机垂直下降速度为vd时的能效系数Kd为
(6)
通过对无人机的3种基本运动进行简化受力分析,得出了无人机运动过程的3个能效系数,为后续路径规划提供参数支撑,同时也能减少路径规划问题的复杂程度。
2 无人机测试及模型拟合
2.1 无人机测试
为获取无人机的运动参数,使用实验室自制的无人机测试装置对四旋翼无人机整体进行测试,以获取无人机的总体升力和功率数据,从而构建无人机功率与升力关系模型。无人机测试装置如图2所示。

图2 无人机测试装置图Fig.2 Diagram of UAV test device1.无人机 2.应变梁传感器 3.无线模块天线 4.支架 5.测试部分电子模块 6.承载板
该装置可以完成无人机电流、电压及升力的实时采集和转换,数据可以实时采集并显示以及存储至计算机。主要参数包括:装置采样频率80 Hz,升力测量量程0~196 N,分辨率0.01 N,电压测量量程0~28.5 V,分辨率0.01 V,电流测量量程0~90 A,分辨率0.1 A。
为了获取无人机的功率与升力,在实验室使用该装置对无人机进行测试。测试时,将无人机固定在测试装置上,使用无人机遥控器的油门摇杆来控制无人机电机的功率,手动将油门摇杆从0均匀缓慢推动至100%(持续时间为30 s),以获取无人机在这一过程中的功率以及与其对应的升力数据,共2 400组。
2.2 无人机功率与升力模型拟合
对无人机测试数据进行处理后,滤除60个异常样本,共获取有效数据2 340组。将该数据随机分成测试集和验证集,其中测试集数据为1 872组,占总数据的80%,用于无人机功率与升力关系模型的构建。以无人机功率P为自变量,无人机升力F为因变量,利用非线性回归方法,使用Matlab软件自带的cftool曲线拟合工具箱对功率和升力关系模型进行拟合,拟合结果如图3所示。
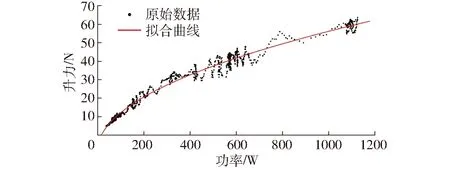
图3 模型拟合结果Fig.3 Results of model fitting
在测试过程中,由于内部飞控对无人机整体转速的调节作用,使得无人机在总升力为45~60 N之间(即功率700~1 100 W)变化较快,因此在该区域内所采集的数据较少。但本研究是对无人机整个范围内的功率与升力关系进行拟合,故在该区域数据较少的情况下也不会影响整体模型的构建。
该拟合结果建立的无人机功率与升力关系模型的表达式为
F=2.061P0.499-8.532
(7)
该模型的决定系数R2为0.989 4,表明该模型具有较良好的拟合效果。
为了对该模型进行验证,基于验证集数据采用异校验的方法进行模型验证。其中验证集数据为468组,占总数据量的20%。以实测升力为自变量,以式(7)计算获得的升力为因变量,进行一次函数拟合,并对计算出的升力与实测升力进行相对误差分析。其模型验证结果如图4所示。
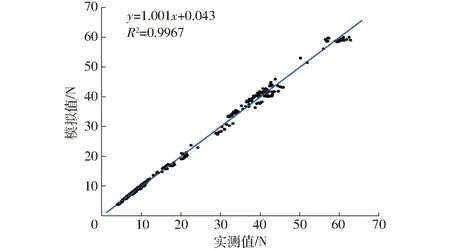
图4 升力实测值与模拟值之间的相关性Fig.4 Correlation analysis of measured and simulated values of lift force
通过对图4所示的升力实测值与模拟值进行相关性拟合,可以得到决定系数R2为0.996 7,拟合曲线的斜率为1.001,纵坐标截距为0.043,表明二者之间存在高度线性相关。同时对验证集数据进行误差分析,升力实测值与模拟值的相对误差的绝对值最大为5.99%。由相对误差和拟合决定系数可知,该模型拟合结果较好,表明所建立的无人机功率与升力关系拟合模型具有较高的精度。
3 能耗最优路径规划
3.1 作业目标获取
为了获取无人机在山地情况下作业时的实际场景,于甘肃省平凉市静宁县山地苹果园(35.16°N,105.77°E,平均海拔1 608 m)进行地形数据获取。该地区果园的地形为阶梯状,果树沿等高线单行种植。为了获取各试验地点三维地形模型,使用DJI Phantom 3 Standard型无人机(深圳市大疆创新科技有限公司)对果园进行航拍获取影像,并基于Agisoft PhotoScan软件(Agisoft,俄罗斯)进行三维地形建模,最终获取高分辨率的数字正射影像(图5a)和数字高程模型(图5b),从而获取每个作业点的经纬度及高程信息。为了便于对目标果树进行路径规划,设定目标点1为作业起降点,以目标点1为原点,将其余39个目标点换算为相对坐标,并利用目标点的相对坐标建立路径规划目标位置的三维数学模型,以满足智能算法对路径规划的需求。最终建立的目标点三维数学模型如图5c所示。
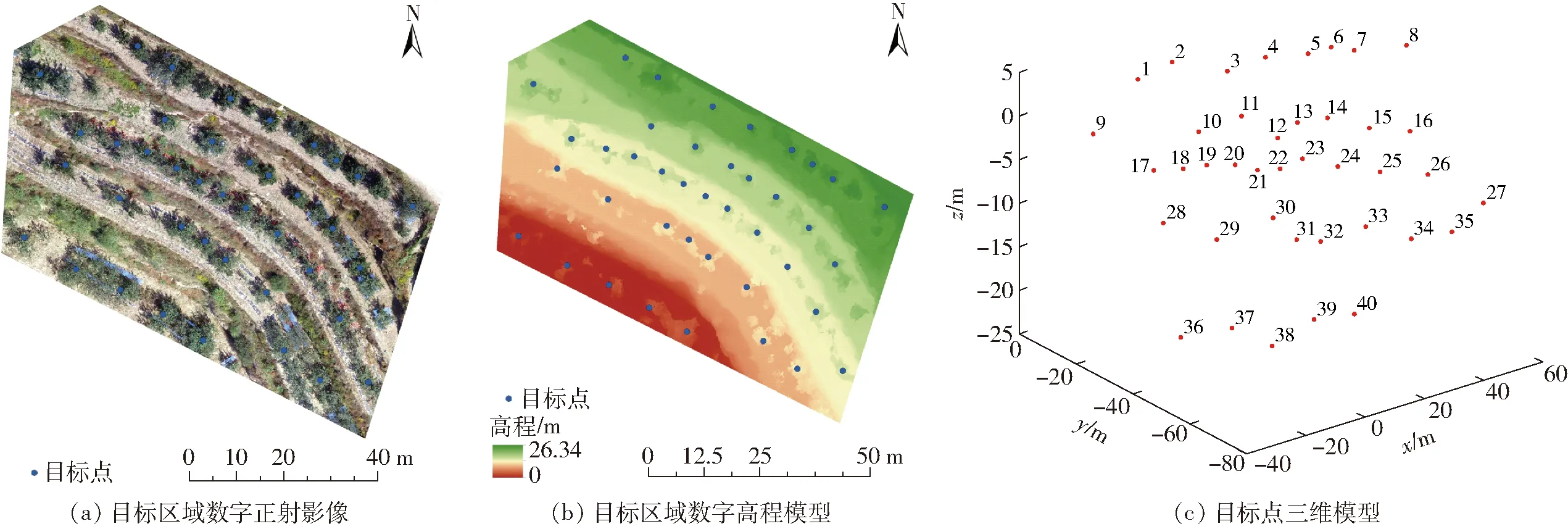
图5 选定区域地形数据Fig.5 Terrain data for selected region
3.2 能效系数获取
本研究中的作业目标点为离散的果树,对于该种作业目标来说,无人机在果树上方作业时可不考虑无人机的偏航过程,因此,本研究中无人机路径规划约束参数使用水平飞行能效系数Kf、垂直上升能效系数Kr和垂直下降能效系数Kd。
为了保证作业效果和安全,无人机在植保作业时的速度较低,一般为2~5 m/s[22-23]。因此在本研究中取水平飞行速度vf=2 m/s,上升速度vr=2 m/s,下降速度vd=2 m/s。由于无人机在水平飞行时其倾斜角较小,加上机身震动等原因,飞行过程中的倾斜角θ和阻力Q难以准确测量,根据经验假设无人机倾斜角θ=5°,其上升和下降时阻力均为其自身重力的5%。
对于40个作业目标点,假设无人机植保作业时负载药量为2 000 g,每个目标点施药量为50 g。为了获取不同负载情况下无人机路径规划算法所需的能效系数,基于式(1)~(7)的受力分析进行相应约束参数的计算。
3.3 算法设计
为了便于智能算法对最优路径进行规划,首先对作业路径进行数学建模,将路径规划问题转化为智能算法可以解决的数学问题。本研究中无人机所需要飞行的目标点位置已知,无人机从固定出发点出发1次且飞过每个目标点仅1次,最后回到出发点,即为搜索自然子集X={1,2,…,n}(X中的元素表示n个作业目标点的编号)的一个排列π(X)={V1,V2,…,Vn},使得Td取最小值[24-25]。
(8)
式中Td——飞行时的总能耗,kJ
d(Vi,Vi+1)——目标点Vi飞到目标点Vi+1的过程能耗,kJ
为了获取无人机从当前目标点飞至下一个目标点的过程能耗d(Vi,Vi+1),基于相对飞行距离和无人机能效系数进行计算,计算公式为
(9)
其中
(10)
式中dx、dy、dz——当前目标点与下一个目标点在x、y、z轴方向的距离,m
(XiYiZi)——当前目标点坐标,m
(Xi+1Yi+1Zi+1)——下一个目标点坐标,m
为了求解能耗最优路径,基于模拟退火算法(Simulated annealing algorithm,SAA)进行寻优。该算法能以较大概率求得全局优化解,且具有较强的鲁棒性、全局收敛性、隐含并行性及广泛的适应性[26-27]。该算法的关键核心为Metropolis判别准则,在本研究中,Metropolis判别准则规定为
(11)
其中
df=Tdnew-Tdold
(12)
式中D——Metropolis判别准则最终接受新路径的概率
Tdnew——新路径的飞行总能耗,kJ
Tdold——上一次路径的飞行总能耗,kJ
T——算法控制参数,即当前温度
由式(11)可知,如果df<0,则以概率1接受新的路径;否则以概率exp(-df/T)接受新的路径。
基于模拟退火算法求解能耗最优路径时,首先对算法进行初始化,即输入目标点的坐标信息并对算法本身控制参数进行赋值,此时的坐标信息中包含无人机在不同负载情况下的两两目标点之间飞行的过程能耗代价。算法初始化完成后开始对路径进行寻优,并利用式(11)的判别准则接受新路径,最终完成最优化能耗路径的获取。优化过程中,令T=qT,即每次循环将当前温度T缩小q倍作为下个当前温度。其算法流程如图6所示。
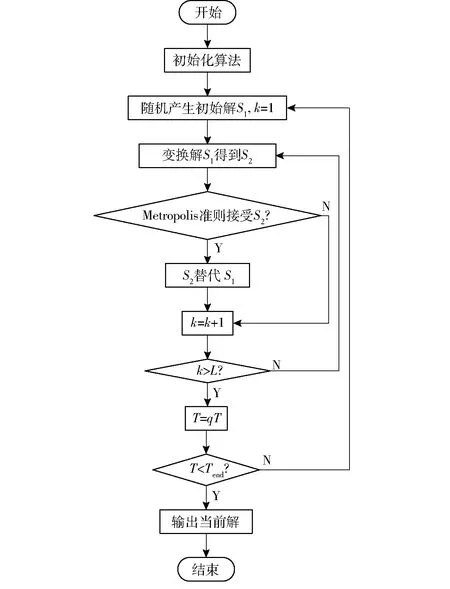
图6 模拟退火算法流程图Fig.6 Flowchart of simulated annealing algorithm
为了提高模拟退火算法在本研究中的求解性能,通过参考该算法常用的控制参数[28],并对本研究中的问题进行多次试验,最终选取的控制参数如下:初始温度T0=1 000;终止温度Tend=0.001;链长L=500;降温速率q=0.9。
3.4 能耗最优路径规划结果
3.4.1不同恒定负载下的路径规划
基于模拟退火算法对作业目标进行能耗最优路径寻优,在此情况下,不考虑无人机的飞行距离,只通过算法获取无人机遍历所有目标点的飞行能耗最优路径。算法对无人机在不同恒定负载情况下的路径规划结果如图7所示。
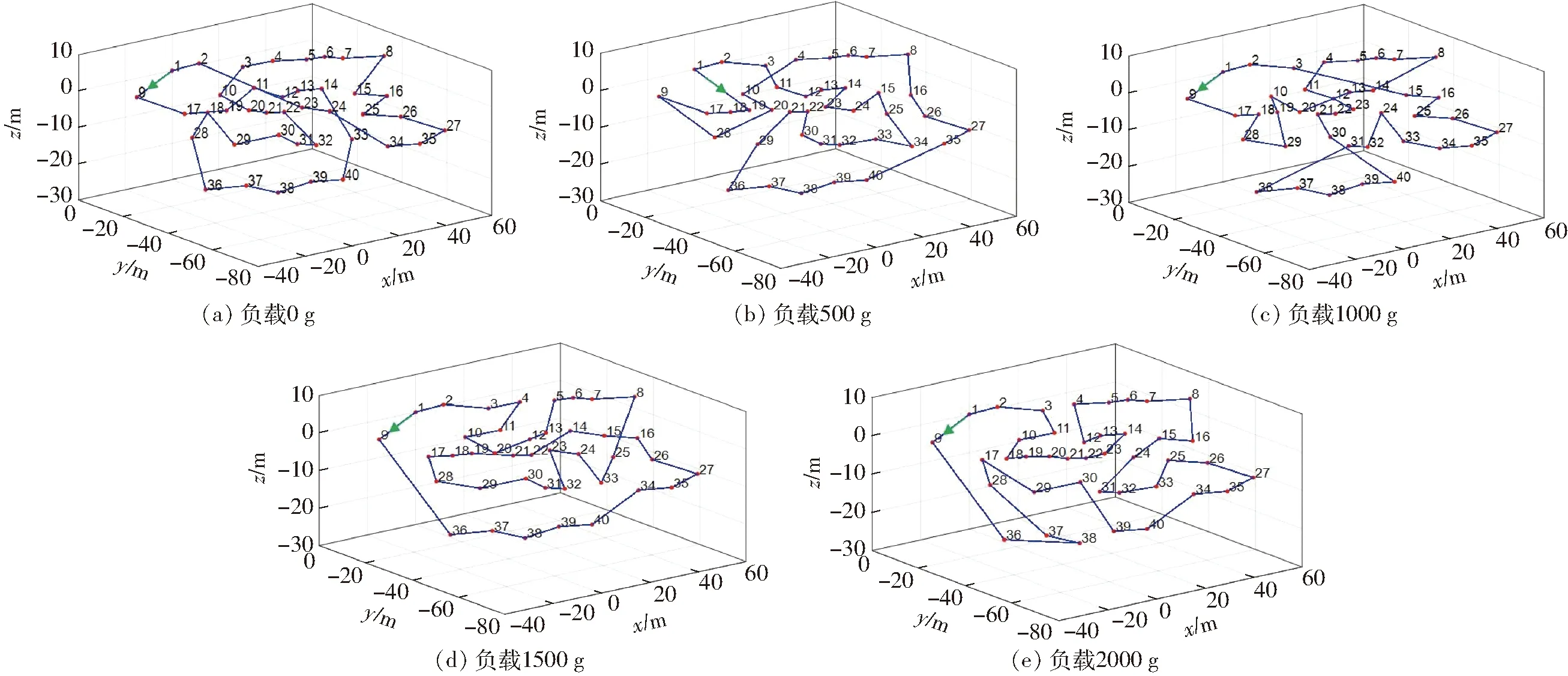
图7 不同恒定负载下能耗最优路径Fig.7 Optimal energy consumption path under different constant loads
由图7可知,无人机在各种不同恒定负载下,算法规划的路径都有相似之处,都是保证无人机优先从起始点向较低高度目标点飞行,即优先产生下降运动,然后尽可能在中间高度位置作业,最后完成较高位置的目标点作业从而回到起始位置。
3.4.2负载实时变化下的路径规划
基于模拟退火算法对作业目标进行能耗最优路径寻优,不考虑无人机的飞行距离,只通过算法获取无人机遍历所有目标点的飞行能耗最优路径。无人机在飞行过程中负载实时变化,无人机在起点时负载为2 000 g,每经过一个目标点后负载减少50 g,以模拟无人机在实际植保作业时的负载实时变化情况。最优路径规划结果如图8所示。
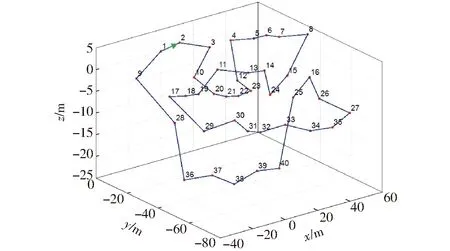
图8 变负载下能耗最优路径Fig.8 Optimal energy consumption path under load fluctuation
从图8中可以看出,在负载实时变化的情况下,算法规划的能耗最优路径与负载恒定的情况下有很大不同。为了使能耗最小,该路径中无人机在前期负载较大时尽可能在同一高度目标点上飞行,以保证较少的上升和下降飞行,且在水平方向上也尽可能减少往复运动;随着负载逐步减少,无人机也随之到达高度较低的目标点位置,最终保证在无人机负载较小的情况下实现最后剩余目标点的作业。
3.5 路径规划结果分析
为了对能耗最优路径规划结果进行对比,本研究采用常见的两种路径作为比较对象。一种为人工操控植保无人机作业时常用的“Z”字形作业路径。无人机按“Z”字形作业路径飞行时,按照图5c中目标点的数字从小到大顺序飞行,即无人机从点1出发,经过所有作业目标点,最终返回起始点1。
其次采用飞行最短路径作为对比,基于模拟退火算法对作业目标进行最短路径寻优,在此情况下,不考虑无人机的能耗,只通过算法获取无人机遍历所有目标点的飞行最短路径。
通过对“Z”字形路径、最短路径以及能耗最优路径下的无人机飞行过程进行分析,计算其在不同负载情况下的飞行总能耗,其结果如表1所示。
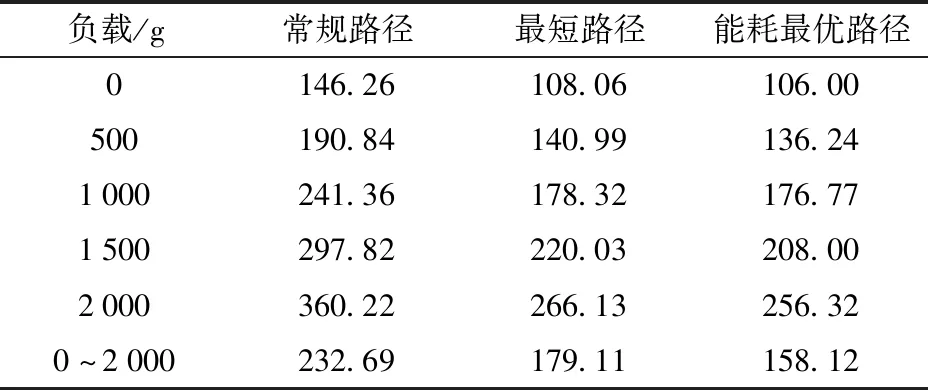
表1 无人机在不同路径下的飞行总能耗Tab.1 Results of total flight energy consumption of UAV under different paths kJ
表1中,负载为0~2 000 g时表示无人机的负载为动态变化,无人机在起始点时负载为2 000 g,每经过一个目标点后负载减少50 g,以模拟无人机在实际植保作业时的负载实时变化情况。其它负载为无人机在该种恒定负载情况下的飞行总能耗结果。
通过对以上无人机在不同负载情况下于不同路径上的飞行总能耗结果进行分析,以常规作业路径和最短作业路径的总能耗为参照,分别计算不同负载情况下模拟退火算法规划的能耗最优路径的能耗节约情况,其计算结果如表2所示。
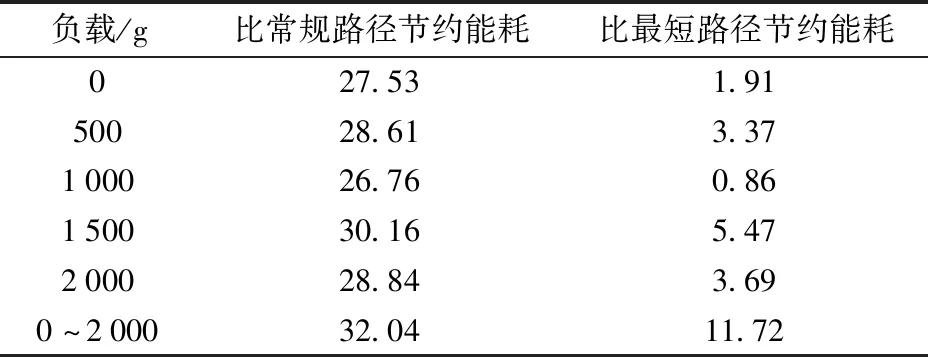
表2 最优路径与其他路径的能耗比较Tab.2 Comparison of energy consumption between optimal path and other paths %
由表2可知,能耗最优路径相较于常规路径的飞行总能耗减少幅度很大,最小为26.76%,最大为32.04%。对于最短路径来说,在负载不变情况下的飞行总能耗减少幅度不大,最大为5.47%,但对于无人机作业负载实时变化的情况下,其飞行总能耗减少幅度较大,为11.72%。在负载实时变化的情况下,以能耗为约束条件进行路径规划时可保证无人机在初期大负载时尽可能的向下飞行,在负载减轻之后再进行水平和上升飞行,因此相较于最短路径仍可以有较大程度的能耗节省。
综上,无人机在恒定负载作业时,基本可以使用最短路径来替代能耗最优路径进行作业,但对于无人机作业负载实时变化的情况下,应使用能耗最优路径进行作业,以降低无人机在作业时的飞行总能耗,从而提高作业效率。
4 结论
(1)对无人机进行运动分析,简化其三维运动过程,并对相应运动过程进行受力分析,从而提出无人机运动过程的3个能效系数,为路径规划问题研究提供参数支撑。
(2)完成无人机功率与升力关系模型的构建。使用测试装置对无人机进行测试,获取了无人机的功率与其对应的升力数据,基于Matlab软件拟合了无人机功率与升力关系模型,决定系数R2为0.989 4,且模型计算值和实测值的相对误差绝对值最大为5.99%,表明建立的无人机功率与升力关系模型具有较高的精度。
(3)基于山地果园的三维地形数据构建作业路径规划模型,并以无人机飞行能效系数为约束条件,设计了可用于无人机三维路径规划的模拟退火算法。
(4)使用模拟退火算法求解能耗最优作业路径,分别对无人机在不同恒定负载、负载实时变化情况下的能耗最优作业路径进行规划。试验表明,在不同恒定负载情况下,能耗最优路径比常规路径最多可节约能耗30.16%,比最短路径最多可节约能耗5.47%;在负载实时变化情况下,能耗最优路径比常规路径可节约能耗32.04%,比最短路径可节约能耗11.72%。说明设计的模拟退火算法可在能耗约束条件下对无人机的作业路径进行规划,且具有较好的规划效果。
