长沙机场阵列天气雷达风场验证

李 渝 马舒庆 杨 玲* 甄小琼4) 乔 丹

1)(成都信息工程大学电子工程学院，成都 610225) 2)(中国气象局大气探测重点开放实验室，成都 610225) 3)(中国气象局气象探测中心，北京 100081) 4)(中国科学院大气物理研究所，北京 100029) 5)(雷象科技(北京)有限公司，北京 100089)

引 言

多普勒天气雷达能获得降水粒子的反射率因子、径向速度和谱宽等，其中径向速度是有效照射体积内降水粒子沿波束方向上的平均速度，但径向速度只是实际风场中的一个分量，不能直接代表实际风。利用径向速度合成或反演三维风场，是雷达气象学中的重要研究方向。精细的三维风场可以研究中小尺度天气系统结构和运动特性。

国内外关于双(多)多普勒天气雷达联合探测风场的研究工作和外场试验已取得一定成果，主要技术方法分为以下3类：①3部或以上多普勒天气雷达直接使用公式合成共同观测区域内的风场，Armijo[1]和Ray等[2]在笛卡尔坐标系下给出求解方程组，韩颂雨等[3]在动态地球坐标系下给出求解方程组；②对于双多普勒天气雷达风场反演方法，Lhermitte等[4]、Chong等[5]、Fankhaus等[6]、刘黎平等[7-8]和罗昌荣等[9]通过双多普勒天气雷达同步观测获得散射体两个方向的径向速度资料,利用这两个方向的资料与其他约束条件(如质量连续方程)联立求解大气风场；③双(多)多普勒天气雷达三维变分(three-dimensional variational data assimilation，3DVAR)风场反演方法。

第3类方法中通常以是否考虑天气系统平移和内演变化情况又分为两类：①未考虑天气系统平移和内演变化。Scialom等[10]对多部多普勒天气雷达进行分析，以标准正交函数的形式建立径向速度的分析模型，将地面边界层约束和质量连续方程作为变分约束加入分析提高垂直速度的反演能力。Gao等[11-12]对双多普勒天气雷达变分反演方法进行优化，其中以质量连续方程为弱约束条件，采用准牛顿共轭梯度算法，通过有限的内存使代价函数最小化提高运算效率。Liou等[13]改善多部多普勒天气雷达变分反演方法的效果，解决传统方法中遇到的迭代不稳定性问题，进一步提高风场反演的精度。王艳春等[14-15]分析双多普勒天气雷达三维变分方法反演风场的能力，误差分析结果表明:水平风速和水平风向的反演结果均比较可靠。但此类方法未考虑雷达体扫时真实天气系统也在快速移动的事实，未进行平流校正，资料时空不匹配会带来一定误差。②考虑天气系统平移和内演变化。Liu等[16]在3DVAR反演算法中加入时间线性插值，它能减少传统方法忽略观测天气系统时间演化的误差，反演结果能捕获到风场的快速演化过程。Shapiro等[17]在3DVAR反演算法中引入泰勒冰冻湍流假设，通过计算两次体扫资料的反射率因子可以大致推导实际数据的时空位置，从而减少反演误差，在不太强的中小尺度天气系统中效果较好。在此基础上，Potvin等[18]进一步优化算法，进行平流校正和内演变化改善，水平风场的平移和演化对于提高垂直风速的反演精度也起到巨大作用，并且得出雷达体扫时间越短，反演效果越好的试验结论。

目前，国内对双(多)多普勒天气雷达3DVAR风场反演方法的外场试验验证研究较少。本文使用部署在湖南省长沙黄花机场的阵列天气雷达资料，由于雷达探测范围较小，且在严格的协同探测模式下3个收发子阵共同覆盖的三维精细探测区域资料时差在2 s以下，保证各个收发子阵同时探测到大气中各点径向速度的空间和时间一致性。这能够减小最终风场合成和反演的误差[19]。目前降水云中真实的三维风场信息很难获得，现有风场观测资料的时空分辨率较低，二者难以匹配，风场的“真值”很难衡量。本文为了验证阵列反演风场的有效性，使用机场1部L波段边界层风廓线雷达产品和阵列合成风场结果作为参考值，与阵列反演风场结果进行相互比较。在3个收发子阵共同覆盖的三维精细探测区域(空间同一点存在3个径向速度时)，将阵列合成风场作为参考值，对阵列反演风场进行验证评估。

1 阵列天气雷达简介和研究个例

本文使用的长沙机场阵列天气雷达由3个相控阵接收发射子阵(简称收发子阵)为一组进行同步探测，在水平方向上每个收发子阵采用机械扫描方式，覆盖0°～360°方位，垂直方向具有4个发射波束和64个接收波束，覆盖0°～90°仰角。每个收发子阵的最大探测距离为20.28 km，径向分辨率为30 m[20]。张沛源等[21]研究3部多普勒天气雷达联合测量大气风场的误差分布及最佳布局，从理论上证明3部雷达以等边三角形布局为最佳。机场阵列天气雷达布局近似于等边三角形(图1)，在3个收发子阵测速精度相同的条件下，能减小风场合成和反演的误差。外场试验中收发子阵天线旋转速度为30°·s-1，1次体扫时间为12 s。单个收发子阵在60°范围内扫描时间为2 s，120°范围内扫描时间为4 s。故在严格的协同探测模式下，3个收发子阵在共同覆盖区域(简称三维精细探测区)的探测资料时差在2 s以下，两个收发子阵共同覆盖区域的探测资料时差在4 s以下。图1中三维精细探测区外也能获取探测资料，这些区域被称为普通探测区。在进行风场合成和反演前，对雷达基数据进行地物杂波滤除、径向速度退模糊等质量控制处理[22]，并且将3个收发子阵的体扫资料通过Cressman方法插值到水平和垂直分辨率均为100 m的直角坐标系网格场中。

图1 3个收发子阵阵列天气雷达布局及探测区示意图(红色矩形为3DVAR风场反演范围，红色圆点为机场风廓线雷达站点)

2019年4—9月长沙机场地区降水较多，也是强对流天气发生最多的月份，本文选取机场外场试验中10次降水过程，按照降水类型分为两类,第1类为稳定性降水，第2类为对流性降水。具体降水个例及时间(北京时，下同)、与风廓线雷达产品对比时段及阵列合成风场与阵列反演风场选用的误差对比分析时刻见表1。

表1 降水个例及描述

2 风场算法简介

2.1 阵列合成风场算法

阵列合成风场计算原理与文献[2]中3部多普勒天气雷达分析方法近似，在插值后的直角坐标系网格场中，每个收发子阵坐标为(xi,yi,zi)，空间任意一点坐标在网格场中表示为(x,y,z)。u，v和w(w=w+wt)代表在x,y,z方向的风分量(wt为降水粒子的下落速度[23])，Ri为网格点到每个收发子阵的距离。每个收发子阵测得的径向速度Vi在直角坐标系中与风分量的公式为

(1)

(2)

联立式(1)和式(2)可在网格场存在3个径向速度时计算出风分量u，v和w。

2.2 阵列反演风场算法

阵列反演风场使用Shapiro等[17]、Potvin等[18]和North等[24]提出的3DVAR风场反演算法，具体算法思想如下：记直角坐标系网格场中每个格点上3个方向的风分量为u，v，w，每个收发子阵坐标为(xi,yi,zi)，空间任意一点坐标在网格场中表示为(x,y,z)。利用径向速度观测约束JO，质量守恒约束JM，地面边界层约束JP和空间平滑约束JS对3个收发子阵的径向速度观测资料进行迭代求解，风场反演结果在J的全局极小值处取得最优解。定义代价函数J：

J(u，v，w)=JO+JM+JP+JS。

(3)

等式右边第1项JO定义为

(4)

(z-zi)[wi-|wti|]}，

(5)

(6)

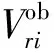
第2项JM定义为

i=1,…,n。

(7)

基态大气参考密度为

(8)

其中，ρs单位为kg·m-3，z单位为m。

第3项JP定义为

(9)

其中，非地面的网格点权重系数设置为0。

第4项JS定义为

+λSw(2w)2,

(10)

(11)

上述公式中，每一项代价函数的权重系数采用North等[24]在外场试验中通过灵敏度分析试验得到的最优解结论。权重系数分别设置为λO=1，λM=500，λP=1，λSu=1，λSv=1，λSw=0.1。

3 三维精细探测区域风场验证

进行三维精细探测区域风场验证前，检查选用个例径向速度资料是否存在较大偏差。具体做法如下：首先，找到两个收发子阵连线上的中点位置A，B，C(子阵1与子阵2、子阵1与子阵3、子阵2与子阵3)；然后，取出该点连续5个时刻不同高度上径向速度的平均值；最后，比较两个收发子阵在该点的值。该位置上两个子阵的径向速度在同一高度的大小应接近且方向相反。雷达的径向速度本身存在观测误差约为1 m·s-1，实际探测中还存在不确定的偏差[25]。因此，径向速度会存在一定范围的偏差。表2中给出个例3在16:00:00—16:00:48连续5个时刻各个收发子阵径向速度的一致性分析结果，可以看出径向速度观测数据无较大偏差。

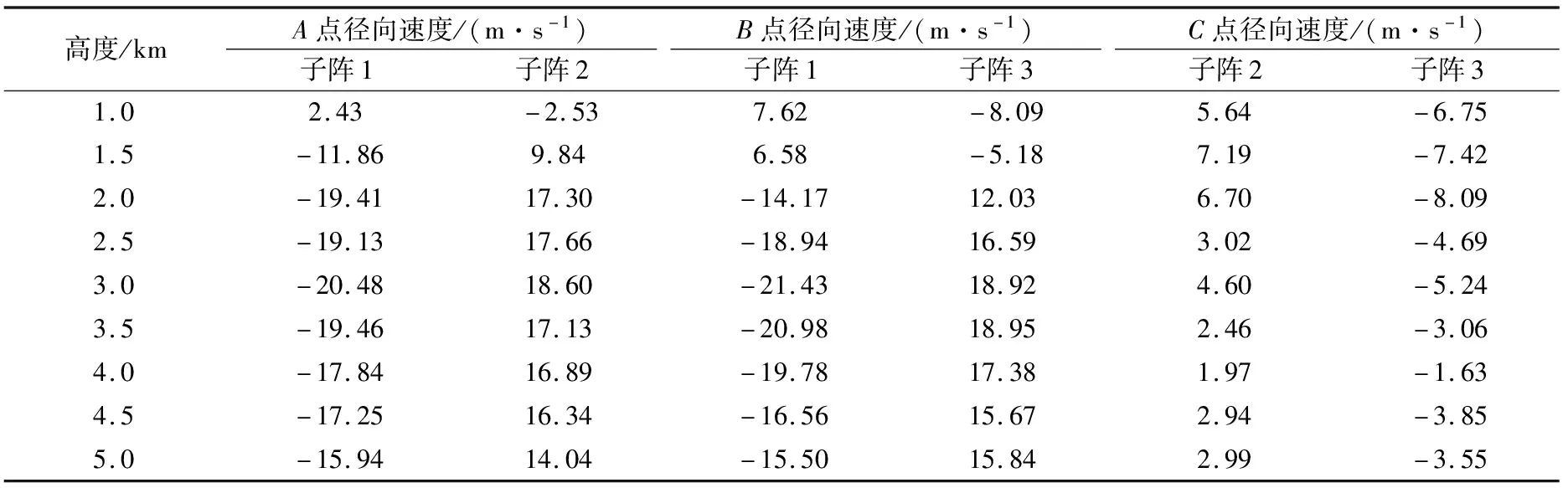
表2 不同子阵连线上中点位置的径向速度一致性分析

3.1 阵列反演风场和阵列合成风场与风廓线雷达产品误差

本节重点讨论阵列反演风场和阵列合成风场与风廓线雷达产品误差，风廓线雷达是风场探测的有利工具[26-28]，其位置见图1红色圆点。精确的探测位置是定点经纬度(28.2°N，113.2°E)上空的风场，高度780 m以下垂直分辨率为60 m，高度780～5220 m 垂直分辨率为120 m。通过风廓线雷达站点经纬度坐标匹配网格场中对应位置，以位置为中心，计算半径R=2500 m内阵列反演和阵列合成风场每一层高度的平均水平风场。降水过程中回波经过此位置上空时间较短，且阵列反演风场和阵列合成风场有时没有风场解，故半径取值较大。分析时间段见表1。选取风廓线不同高度随时间变化的风场产品作为参考值与阵列反演风场和阵列合成风场进行相互比较。采用平均绝对偏差、均方根误差、相对均方根误差(相对参考值的均方根误差百分比)3个评价参数分别评估分析时间段内水平风速和水平风向两个物理量，水平风向的平均绝对偏差和均方根误差已经能客观表现风向误差，不再计算水平风向的相对均方根误差。

3.1.1 稳定性降水

表1中有5次稳定性降水过程，图2是个例3在2019年5月12日15:30—17:30时段，风廓线雷达产品、阵列反演风场和阵列合成风场在风廓线站点上空高度随时间变化的水平风场(风羽)。为了与风廓线雷达产品5 min 的时间分辨率匹配，本文选择最接近风廓线雷达探测时间的阵列天气雷达资料进行对比。图2中水平轴时间间隔为5 min，垂直轴高度间隔为500 m，无风矢的位置表示无风。

由图2可看到，风廓线雷达产品、阵列反演风场和阵列合成风场的水平风速在1 km和1.5 km高度存在差异，但风向随高度变化趋势一致。3种方法在2～5 km 高度表现为均匀的西南风，风速、风向相近。在风场均匀的降水过程中，风廓线雷达测风精度较准确[29]。将风廓线雷达产品的水平风作为参考值，分别计算阵列反演风场和阵列合成风场5个个例分析时间段内水平风速和水平风向的平均绝对偏差和均方根误差以及水平风速的相对均方根误差。由表3可见，阵列反演风场风速和风向的平均绝对偏差分别为1.28～3.96 m·s-1,5.72°～10.81°，表明水平风在分析时段变化不大。表3中水平风速的均方根误差为2.14～3.92 m·s-1，相对均方根误差为19%～31%。阵列反演风场的水平风速存在一定误差，但相对偏差在31%以下，水平风速比较合理。水平风向的均方根误差为7.56°～17.69°，与风廓线雷达产品的风向差小于20°，风向表现较一致。阵列合成风场的误差评价参数差别不大(表略)，说明阵列反演和阵列合成风场比较一致。可认为风廓线雷达产品，阵列反演风场和阵列合成风场3种方法的结果较一致。

图2 2019年5月12日15:30—17:30不同高度的水平风场(a)风廓线雷达产品，(b)阵列反演风场，(c)阵列合成风场

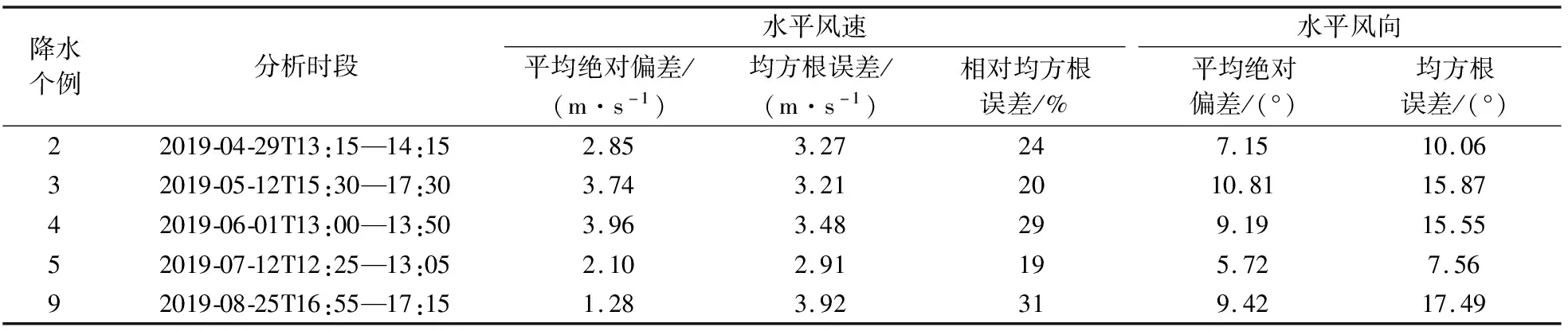
表3 个例分析时段内阵列反演风场与风廓线雷达产品水平风速和水平风向的平均绝对偏差、均方根误差和相对均方根误差

3.1.2 对流性降水

表1中有5次对流性降水过程,由于个例8降水回波未经过风廓线雷达站点上空，所以只对其余个例进行对比分析。图3为个例1在2019年4月26日18:00—20:00 时段风廓线雷达产品、阵列反演风场和阵列合成风场在风廓线站点上空高度随时间变化的水平风场(风羽)。可以看到，在18:00—18:30风廓线雷达产品风场出现较大变化，阵列反演风场和阵列合成风场整体变化趋势不大。与风廓线雷达产品相比，阵列反演风场和阵列合成风场(表略)的误差评价参数差别不大，说明阵列反演和阵列合成风场比较一致。表4中风速和风向的平均绝对偏差分别为1.52～2.94 m·s-1和39.79°～55.89°，表明在分析时段内水平风速变化不大，但水平风向变化显著。表4中水平风速的均方根误差为2.66～5.57 m·s-1，相对均方根误差为44%～73%；水平风向的均方根误差为33.88°～58.24°。表明水平风速和水平风向在误差参数评价下表现不好，与风廓线雷达产品相比误差较大。对流性降水出现时环境风场不均匀会造成风廓线雷达测得的水平风向、风速的测量误差较大，测风精度下降[29]，故在对流性降水过程中，风廓线雷达产品与阵列反演风场和阵列合成风场差异较大。但阵列反演风场和合成风场在风廓线站点上水平风表现较一致，也验证了在降水场很不均匀时风廓线反演的水平风会出现误差的事实。

表4 个例分析时段内阵列反演风场与风廓线雷达产品水平风速和水平风向的平均绝对偏差、均方根误差和相对均方根误差

图3 2019年4月26日18:00—20:00不同高度的水平风场(a)风廓线雷达产品，(b)阵列反演风场，(c)阵列合成风场

3.2 两种风场算法的误差分析

本节重点讨论两种风场算法对不同降水类型求解的水平风速与水平风向误差。为了将阵列合成风场作为参考值，本节阵列反演风场只计算有3个径向速度存在的网格点，保证误差计算过程中两种算法均在有风场解的格点进行对比。降水类型虽不同，但两种风场算法在同一时刻求解结果应接近。不同时刻的误差分析结果差别不大，以10次降水过程中某一时刻的计算结果为例进行误差分析，选用的对比体扫时刻见表1，误差评价参数与3.1节中一致。

3.2.1 稳定性降水

风场求解区域为图1中红色矩形区域，网格场水平范围大小为25 km×25 km，高度为20 km，水平和垂直方向网格间距均为100 m。选取表1中5个稳定性降水过程，图4为各个高度层水平风速和水平风向的均方根误差，以及水平风速的相对均方根误差。由图4可以看到，水平风速的均方根误差为0.36～2.28 m·s-1，相对均方根误差为1%～19%；水平风向的均方根误差为1.51°～14.92°。水平风速的相对偏差低于20%，水平风向差小于15°，即在稳定性降水条件下水平风速和水平风向在各个高度层较为一致，误差较小。

图4 5个稳定性降水个例误差(a)水平风速均方根误差，(b)水平风速相对均方根误差，(c)水平风向均方根误差

2019年8月25日16:50—18:20阵列天气雷达探测到降水回波自东移入三维精细探测区，向西南方向发展。风场与回波移动方向几乎一致，低层为均匀的东北风，中高层转为偏东风。图5a、图5b为8月25日17:05:12阵列合成风场和阵列反演风场在3 km，5 km高度上的水平风羽图，选取红色矩形区域内10 km × 10 km范围进行展示。由图5可知，3 km高度为均匀的东北风，5 km高度为比较均匀的偏东风。两种算法的水平风场空间分布和大小方向非常接近，在视觉上看不出明显差异。

图5 2019年8月25日17:05:12阵列合成风场和阵列反演风场不同高度的水平风矢(填色为反射率因子)(a)阵列合成风场,3 km高度，(b)阵列反演风场,3 km高度，(c)阵列合成风场,5 km高度,(d)阵列反演风场,5 km高度

3.2.2 对流性降水

与3.2.1节一致，将阵列合成风场作为参考值，选取表1中5个对流性降水过程求解的阵列反演风场进行误差分析。对流性降水过程中回波强度大、持续时间短、随时间变化迅速，且风场复杂多变。图6为各个高度层水平风速和水平风向的均方根误差，以及水平风速的相对均方根误差。由图6可知，水平风速的均方根误差为0.19～3.73 m·s-1，相对均方根误差为1%～29%；水平风向的均方根误差为2.04°～26.35°。水平风速的相对偏差低于30%，水平风向差小于30°。与稳定性降水过程相比，水平风向差出现较大差异是由于阵列合成风场是计算网格场中每一个点的风分量，而阵列反演风场是网格场中全局风分量的最优解，式(10)中还对结果进行平滑处理。故在对流性降水过程中，阵列反演风场的每个格点风向经过平滑后比阵列合成风场整体偏向更为一致。结果表明：两种算法在对流性降水条件下，水平风速和水平风向在各个高度层较为合理。与稳定性降水过程相比，对流性降水水平风速和水平风向误差略大。

图6 5个对流性降水个例误差 (a)水平风速均方根误差，(b)水平风速相对均方根误差，(c)水平风向均方根误差

2019年8月21日14:00—16:00中等强度的分散对流云团在三维精细探测区内以40 km·h-1的速度向南偏西方向移动，其间存在短时强降水并伴有雷暴天气。图7为8月21日14:52:00时刻阵列合成风场和阵列反演风场在3 km和5 km高度上的水平风羽图。由图7可知，局地强回波位于三维精细探测区之间，周围为层云区，中心最强回波超过45 dBZ。从风场结构看，两种算法结果比较一致。3 km和5 km高度分别以东北风和偏东风为主，而且出现明显的涡旋结构(图7中红色圆圈)；风速、风向变化大，且在强回波区域风速较大。总体上，从视觉上看风场细节存在差异，但空间分布较一致。

图7 2019年8月21日14:52:00阵列合成风场和阵列反演风场不同高度的水平风矢(填色为反射率因子)(a)阵列合成风场,3 km高度，(b)阵列反演风场,3 km高度，(c)阵列合成风场,5 km高度,(d)阵列反演风场,5 km高度

4 结论与讨论

利用2019年4—9月高时空分辨率的阵列天气雷达资料开展3DVAR风场反演。为探讨其结果在不同降水类型下的反演能力，选用10个降水个例，在三维精细探测区采用1部L波段边界层风廓线雷达产品和阵列合成风场作为参考值对其进行验证评估。得到以下结论：

1)在稳定性降水条件下，反演和合成结果与风廓线雷达产品较为一致，比较合理。在对流性降水条件下，得到的结果误差较大。由于在对流性降水中环境风场不均匀性会造成风廓线雷达测风精度下降，与阵列反演和阵列合成风场相比出现较大差异。

2)对比不同降水条件下的阵列反演风场与阵列合成风场，两种算法得到的风场结构符合各类天气系统的基本特征，水平风场的空间分布和风速、风向非常相近。

3)在稳定性降水条件下，两种算法得到的水平风速相对偏差低于19%,水平风向差小于14.92°；在对流性降水条件下，两种算法得到的水平风速相对偏差低于29%,水平风向差小于26.35°。总体上，两种算法效果较一致，误差在可接受范围内，阵列反演风场在稳定性降水条件下优于对流性降水。

尽管本文已对阵列天气雷达反演风场的结果进行不同的验证评估，但由于外场观测资料时空分辨率不匹配和分析方法有限，仍存在不足：①由于计算原理不同，利用阵列合成风场对阵列反演风场进行定量评估，无法对两个子阵共同覆盖的区域进行误差分析；②风廓线雷达与阵列天气雷达的测风原理不同，与风廓线雷达产品对比分析时未考虑稳定性降水和对流性降水过程的不同偏差，后期还需完善资料对比分析的相对偏差统计，从而进一步提高阵列天气雷达反演风场的准确性和实际应用的可靠性；③将阵列天气雷达资料从极坐标系插值到直角坐标系中存在一定误差，导致求解的风场结果也有误差；④目前，阵列天气雷达反演风场研究中的降水粒子下落末速度是以雷达反射率因子参数化进行估计，降水粒子下落末速度计算如果存在较大误差会影响最终垂直速度的结果。本文未对垂直速度进行验证分析，未来将开展对降水粒子下落末速度的估算，进一步讨论反演垂直速度的准确性和合理性。