基于重置顶点下标的网络最大流算法

2020-10-28罗甜甜赵礼峰

计算机技术与发展 2020年10期

罗甜甜，赵礼峰

(南京邮电大学理学院，江苏南京 210023)

0 引言

最大流问题是一种组合最优化问题，在许多实际的网络系统中都存在着流量和最大流问题，例如铁路运输系统中的车辆流[1-3]、城市排水系统中的水流问题[4-6]、控制系统中的信息流问题等[7-9]都可以抽象出最大流模型，从而转化为最大流问题。所以最大流问题应用广泛，实践性强。求解网络最大流的常用算法可以分为增广路径算法和预流推进算法[10]。其中后者的编码程度过高，因而前者为经常使用的算法。而属于增广路径算法的主要有：Ford-Fulkerson算法[11]，Edmonds-Karp算法和最短增广链算法[12]，ISAP算法。设容量网络D的顶点数为m，弧数为n，弧容量的最大值为cmax，Ford-Fulkerson算法的算法复杂度则为O(mncmax)，当容量网络某些弧容量为无理数时，此算法便会陷入无限循环。Edmonds-Karp对其修正，用宽度优先取代了深度优先。最短增广链算法是将顶点按照其与源点的最短距离分层，分层时用宽度优先法，而寻求增广路径时采用深度优先策略。两者结合效率明显高于Edmonds-Karp算法。ISAP算法是对最短增广链算法的优化，即通过深度优先不断修改距离标号的方式省去每一次的宽度优先。但由于最短增广链算法在构建分层剩余网络中选取增广链仍然存在随机性使得某些增广链缺失，导致算法执行后的结果偏小，失去其准确性。

该文针对最短增广链算法在分层剩余网络后寻找增广链不考虑先后顺序使得最大流值偏小这一问题进行改进，沿用了最短增广链算法通过宽度优先将顶点分层的思想，将顶点根据层数，源弧容量，汇弧容量和顶点容差这四个因素来确定顶点被选择的先后顺序。然后根据相应规则来选取增广链，此规则可以保证最短增广链优先选取，并可以井然有序地快速找出所有增广链。

1 基本概念

定义1[13]：容量网络D=(V,A,c)，其中V表示D中顶点的集合，A为D中弧的集合，c表示弧上的容量。

定义2[13]：流量。设f是容量网络D中弧集A上的一个实函数，∀a=(vi,vj)∈A，记f(a)=fij。如果函数f={fij|(vi,vj)∈A}满足守恒条件：

则称f是D的一个流，此时，fij称为通过弧(vi,vj)上的流量。

定义3[13]：顶点层数：在容量网络D中，用宽度优先搜索[14-15]找出从源点vs到任意一点vi(vi∈V)的最短路的长度hi称为顶点vi的层数，即由vs到vi的路径中所含的最少弧数。(第零层只有一个节点就是源点即hs=0)。

定义4[16]：剩余网络D(f)=(V,A(f),cf),其中V表示容量网络D中顶点的集合，f为D上的可行流，A(f)是D(f)上弧的集合，其中，

A(f)=A+(f)∪A-(f)

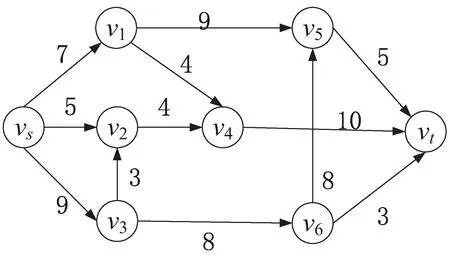
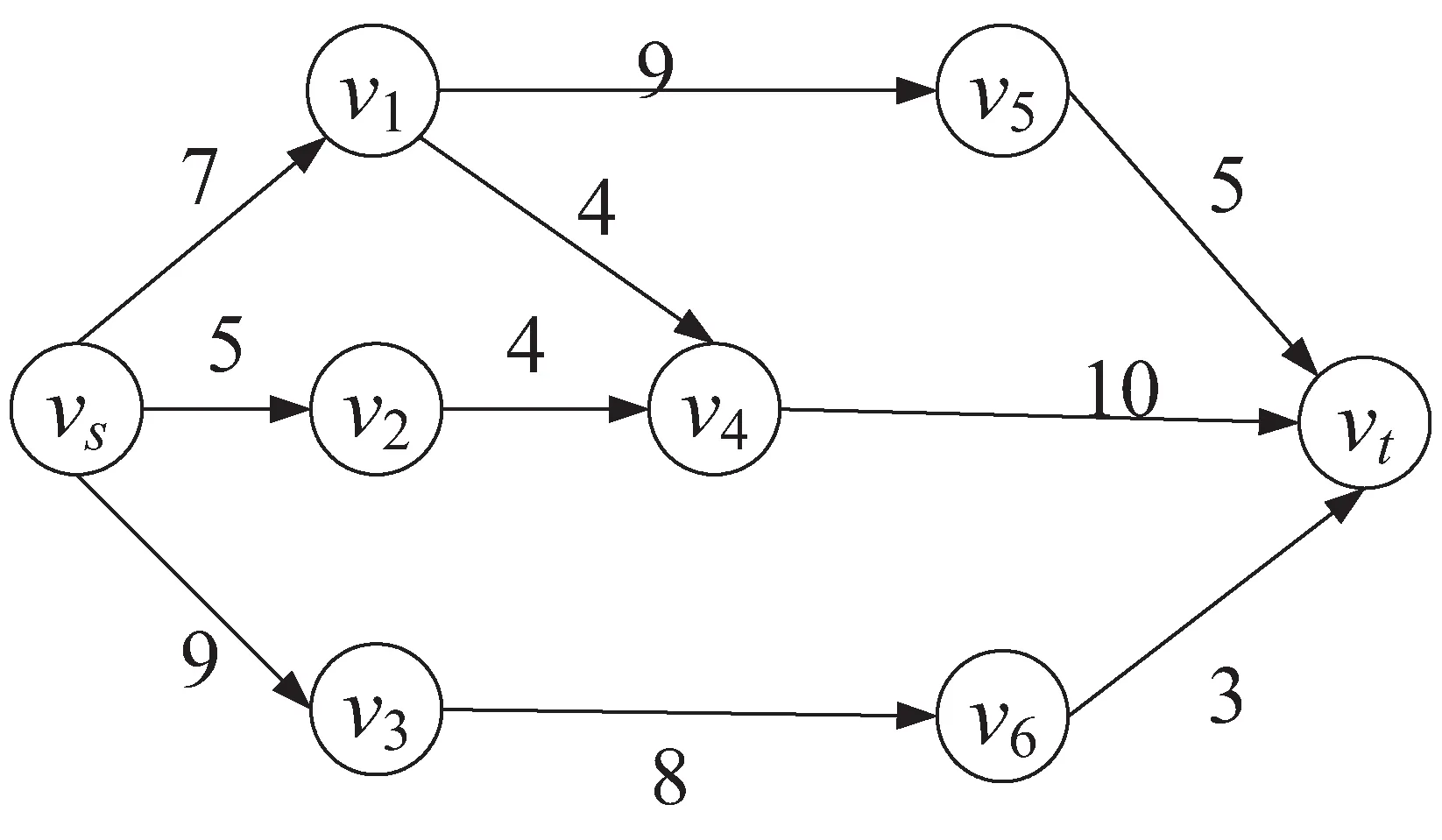
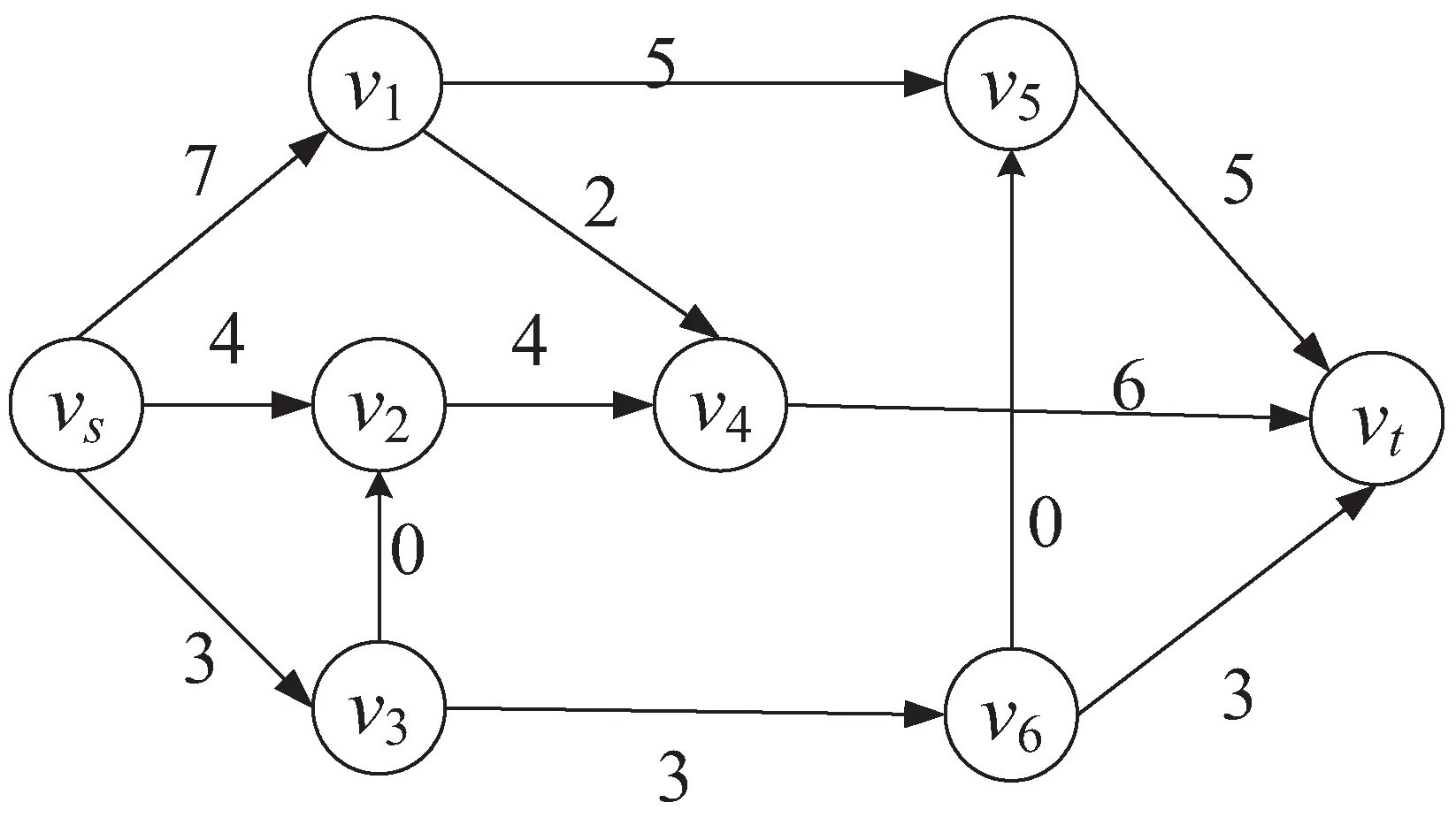
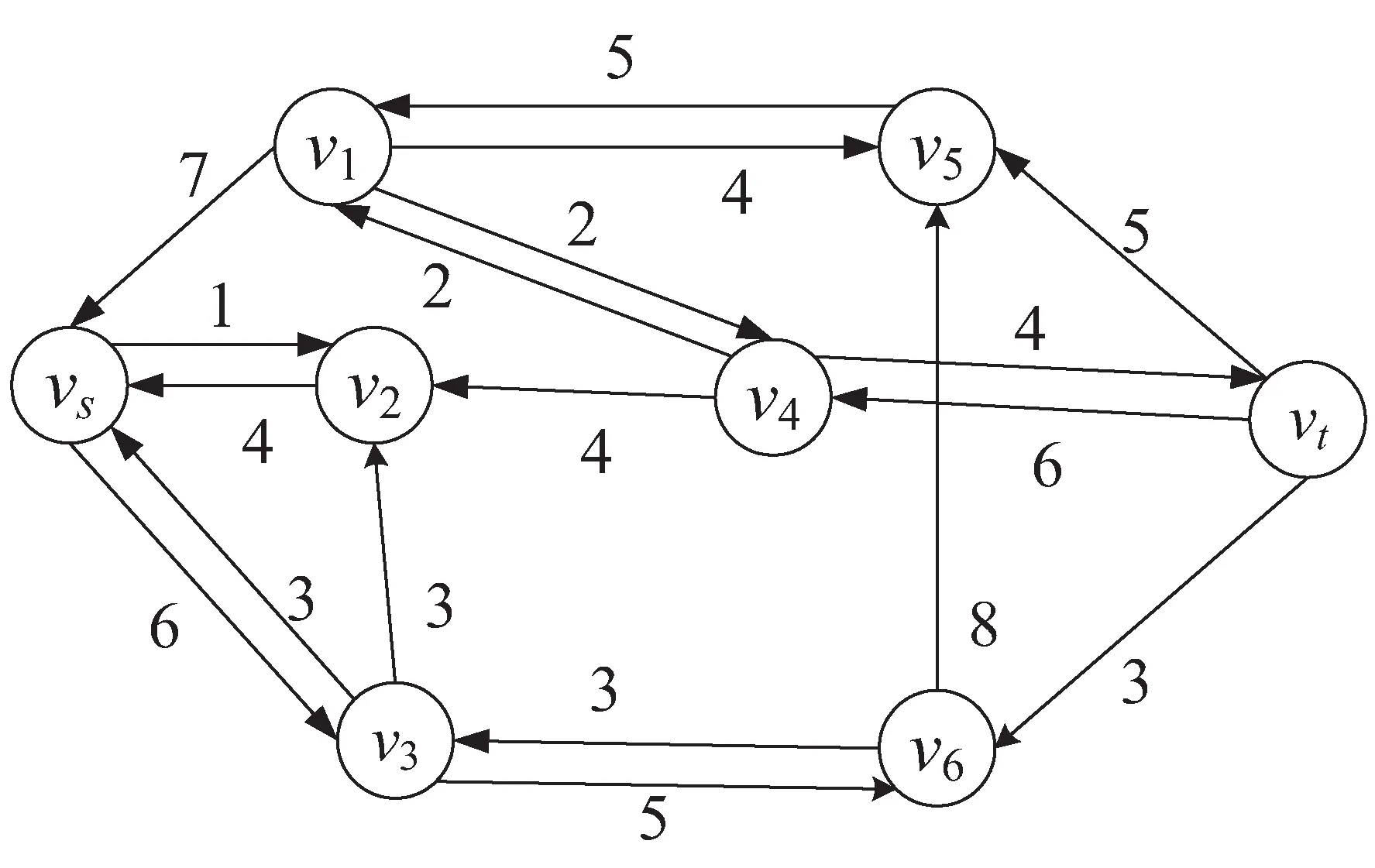
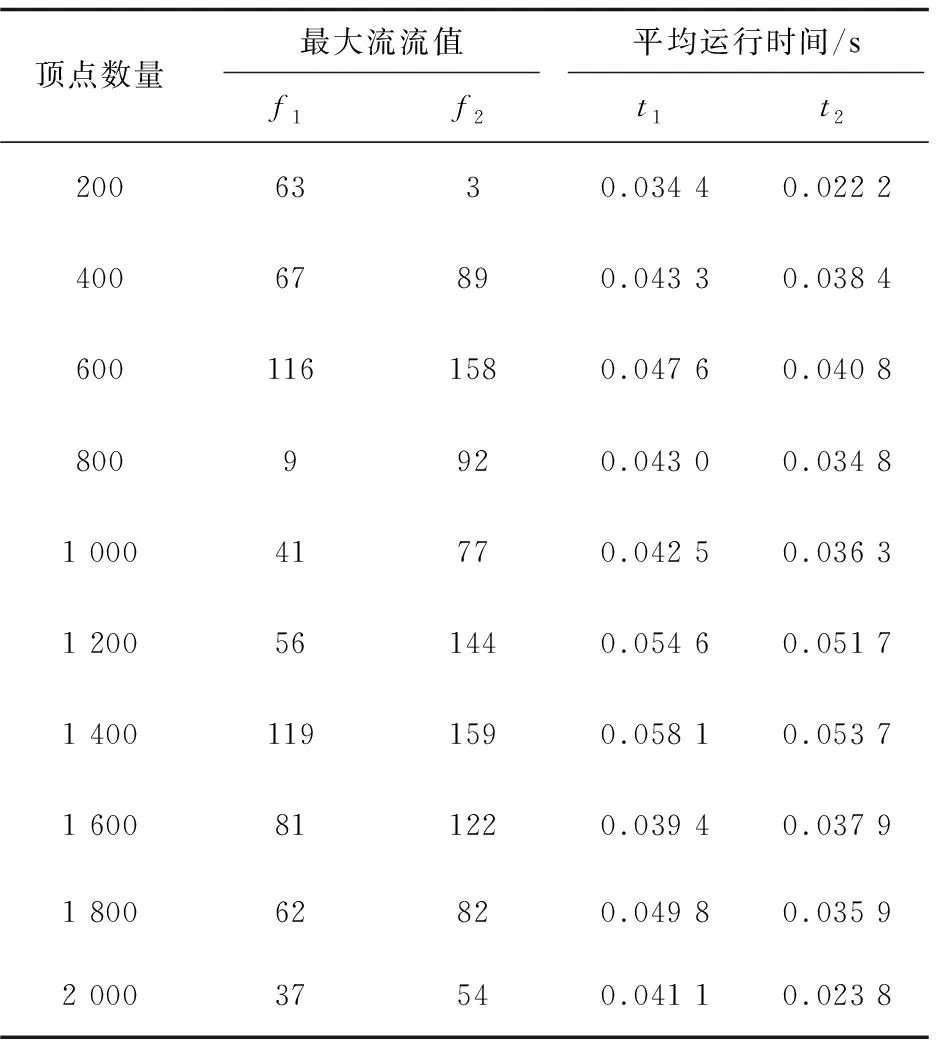
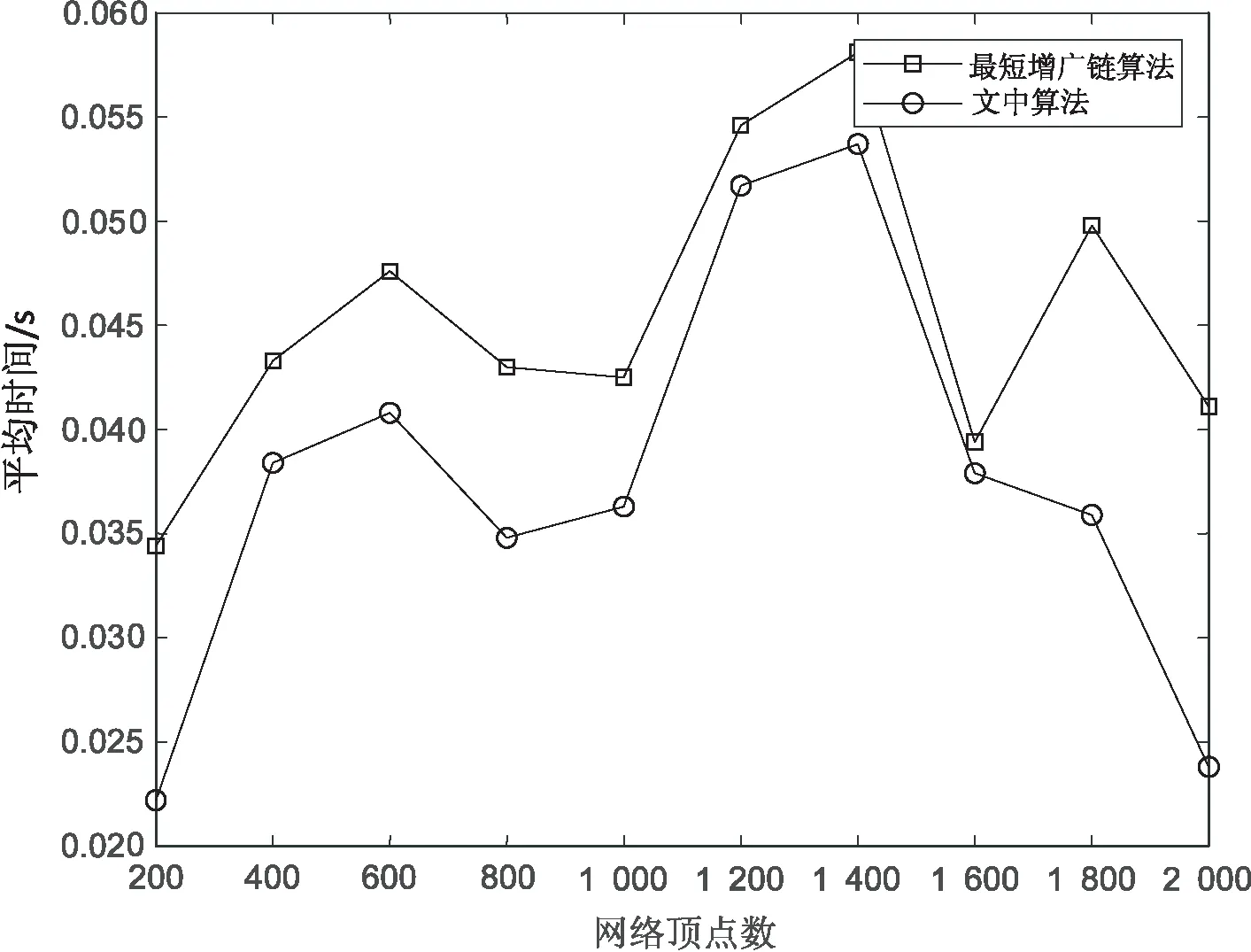
A+(f)={(vi,vj)|(vi,vj)∈A,fij

A-(f)={(vi,vj)|(vj,vi)∈A,fij>0}

cij(f)为(vi,vj)关于f的剩余容量，其中，

定义5[16]：分层剩余网络记为AD(f)=(V'(f),A'(f),cf)，其中，

V'(f)={vt}∪{vi∈V|h(vi)

A'(f)={(vi,vj)∈A(f)|h(vj)=h(vi)+

∪{(vi,vt)∈A(f)|h(vi)=h(vt)-1}

定义6：源弧容量：由源点vs到顶点vi(vi∈V)所构成的弧的容量c(vs,vi)，记为αi。

定义7：汇弧容量：由顶点vi(vi∈V)到汇点vt所构成的弧的容量c(vi,vt)，记为βi。

定义8：顶点容差：顶点vi(vi∈V)的所有出弧容量减去该顶点的所有入弧容量的值为顶点vi(vi∈V)的容差，记为γi。

定义9：中间顶点(除源点、汇点外)标号过程：对于顶点vi，当hi=1时，求出αi和γi，将其标号为(1,αi,γi)；当1

定义10：重置顶点下标规则：已知网络D，其顶点数为n，则将源点vs重置为v1，汇点vt重置为vn。除源点汇点外，中间顶点的重置标号依次为v2,v3,…,vn-1。首先按照顶点层数hi由低至高的顺序依次由小到大编号重置；当hi相等时，分三种情况考虑：

(1)hi=1，按照源弧容量αi由低至高的顺序依次由小到大编号重置，当αi相等时，再按照容差γi由低至高的顺序依次由小到大编号重置；

(2)当最高层的顶点唯一，且13)时，当最高层顶点不唯一，且13)时，都按照容差γi由低至高的顺序依次由小到大编号重置；

(3)当最高层的顶点唯一，且hi=ht-1时，或者当最高层的顶点不唯一，且hi=ht时，都按照汇弧容量βi由低至高的顺序依次由小到大编号重置，当βi相等时，再按照容差γi由低至高的顺序依次由小到大编号重置。

定理：设f是容量网络D中的可行流，则f是D的最大流当且仅当D中不存在f增广链。

2 新算法思想及步骤

2.1 算法思想

求网络最大流[17]的基本思想是根据定理1，即从容量网络D中的一个可行流出发，寻找增广链进行增广，直至D中不存在增广链为止。根据此思路，目的是寻找增广链，关键是确定选取增广链的先后顺序。首先是根据一定规则对顶点下标进行重置，形成与原网络D相对应的新网络D1。然后按照优先选取顶点标号值较大的增广链增广的原则在D1中寻找增广链，直至不存在从源点到汇点的增广链即可结束该算法。

2.2 算法步骤

Step1:利用宽度优先搜索求出原容量网络D中各个顶点的层数，再根据定义9对中间顶点进行标号。

Step2：根据定义10对顶点下标进行重置，形成对应的新网络D1。

Step3：初始化新网络D1，令D1中每条弧的流量为0。

Step4：从顶点v1出发，判断D1中是否存在一条从v1到vn(n为网络D1的顶点个数)的增广链，若存在转Step5，否则转Step7。

Step5：从顶点v1出发，沿着与其关联弧所在顶点下标值较大的原则找一条从v1到vn的增广链，若存在转Step6，否则转Step7。

Step6：调整，求该链上各弧容量的最小值δ，并将此增广链中对应弧的容量后面标上δ，其中δ=min{cij-fij}。在饱和弧上标上终止弧标志“||”，增广后转Step4。

Step7：计算所有以v1为发点的弧的流量和，得到最大流值v(f)，算法结束。

3 新算法可行性与复杂度分析

3.1 可行性分析

新算法的主要思想是沿着所规定好的原则寻找增广路径，每次增广至少使一条弧达到饱和。假设网络D中共有m条弧，那么最多通过m次增广后，网络D中就不存在从源点到汇点的增广链，即算法结束。说明算法经过有限次步骤就会终止，不会陷入无限循环。

3.2 复杂度分析

新算法主要分为两个过程：一是标记、比较和编号过程，通过这些准备工作构建新网络流图；二是增广过程，沿着顶点下标值大的原则寻找增广链。设容量网络D的顶点数为n，弧数为m。该算法执行时，第一个过程属于准备过程只执行一次，而执行一次准备工作的计算量分别是：(1)计算层数O(n)次；(2)计算容差最多需要O((n-2)m)次；(3)比较大小重新编号最多需要O(2nlog2n)次。第二个过程最多执行O(m)次，于是该算法的时间复杂度为：

O(n)+O((n-2)m)+O(2nlog2n)+O(m)=O(2nlog2n+nm)

4 应用实例

例：求出图1的容量网络D中从源点vs到汇点vt的网络最大流。

图1 容量网络D

解：方法一(文中算法)：

(1)首先根据宽度优先搜索求出各顶点层数，得：

(2)对于hi=1，要求出αi和γi，于是可得：

因为ht=3<4，对于1

(3)由(2)所得数据对顶点标号，如图2所示。

图2 标号后的容量网络D

(4)再根据定义8重置顶点下标：令

重新构造容量网络D1，如图3所示。

图3 容量网络D1

(5)在D1中按照优先选取顶点下标值较大的原则寻找增广链：

增广后的网络流图如图4所示。

图4 可行流f

在图4中找不到v1到v8的增广链了，故图4即为最大流f，计算最大流值为V(f)=4+3+3+5+1=16。

方法二(最短增广链算法)：

(1)在D中取f1为初始可行流，令f1为零流。然后构建分层剩余网络AD(f1)，见图5。

图5 分层剩余网络AD(f1)

(2)在图5中找增广链，找到了如下几条增广链：

增广之后，得到可行流f2，见图6。

图6 可行流f2

(3)继续构建剩余网络D(f2)，见图7。发现D(f2)中不存在(vs,vt)路，算法结束。f2即为容量网络D的最大流，在图6中计算与源点关联的所有弧的流量和为14，即最大流的流值为14。可见与方法一相比流值偏小。

图7 剩余网络D(f2)

5 算法的仿真与比较

5.1 实验环境与设计

该算法使用的实验仿真平台是MATLAB2016a，处理器为Intel(R) Core(TM) i3-4030U CPU @1.90 GHz，内存4 GB，Windows7版本64位操作系统。

仿真实验采用的是BA无标度随机网络，并将网络规模的顶点数依次设为200，400，600，800，1 000，1 200，1 400，1 600，1 800，2 000。然后在给定的网络规模下，对新算法和最短增广链算法进行10次仿真实验。其中参数f1和t1分别表示最短增广链算法的最大流值和它的运行时间的平均值，参数f2和t2分别表示新算法的最大流值和其运行时间的平均值。