船舶推进电机运动控制系统仿真研究

李 浩，王 川，郭昊昊，刘彦呈，包芳泉，张珍睿

(大连海事大学 轮机工程学院，辽宁大连 116026)

0 引 言

随着现代交流技术的飞速发展，电力推进型船舶逐渐走入航运市场。由于永磁材料工艺、控制技术、电力电子技术的发展，永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）在电力推进型船舶中的应用也愈发广泛[1]。伴随着永磁同步电机应用范围的不断扩大，其调速控制策略也在研究和探索的过程中不断提出。其中，矢量控制是公认最有效的永磁同步电机控制策略之一[2]。而就电力推进型船舶本身而言，其拥有传统柴油机推进型船舶所无法比拟的优点[3]。因此为了更好地发展电力推进型船舶，如何建立有效的船舶推进电机运动控制系统的仿真模型具有重要意义[4]。

为了建立合适的船舶推进电机运动控制系统仿真模型，国内外学者开展了相关研究。文献[5-6]对螺旋桨负载特性方面进行仿真研究，但缺乏对电机控制方面的研究；文献[7]基于直接转矩控制理论分析船舶交流电力推进系统，但并未给出整体调速系统模型；文献[8]采用永磁同步电机对螺旋桨负载特性进行仿真模拟，却未给出永磁同步电机的具体相关参数；文献[9]虽然设计了船舶电力推进仿真系统，但并未给出实验结果。除上述以外，国内外在对电力推进型船舶控制系统进行建模仿真时，绝大部分是基于Matlab/Simulink 软件平台下搭建相关模型。而由于在Simulink 中很多模块是现成封装好的，内部模型不公开，不便于程序调试，同时与其他算法程序接口匹配困难。

针对上述问题，本文采用Matlab 脚本语言编程方式，基于牛顿拉夫逊法求解矢量控制下差分化的永磁同步电机方程组，通过搭建船机桨一体数学模型，分析船机桨在不同工况下的动态响应。本文采用全代码方式的仿真也使得整个过程可视易调，可以十分便捷地增加控制算法，仿真结果也验证了该模型和方法的正确性。

1 船舶电力推进系统建模

当选用低速电机作为船舶推进电机时，减速机构可被省略，螺旋桨直接通过联轴器与电机相连，因此两者转速一致。本文以永磁同步电机为推进电机，船桨运动产生的转矩作为推进电机的负载输入转矩，其整体运动控制系统框图如图1 所示。

图1 船舶推进电机运动控制系统框图Fig.1 The diagram of ship propulsion motor motion control system

1.1 永磁同步电机控制系统建模

由于永磁同步电机具有非线性、强耦合的特点，为简化其模型，通常依据矢量控制的思想，利用坐标变换的方式将三相固定坐标系下电机数学模型转换为两相旋转坐标系下的电机数学模型，从而使得其中部分变量解耦，达到类似直流电机调速系统的控制效果。依据图1 所示搭建静止坐标系下的永磁同步电机模型，由于2 次坐标变换会导致计算繁琐。为了简化后期控制器的设计，本文选择在同步坐标系dq 轴下搭建PMSM 数学模型。PMSM 数学模型应当包括电压方程、磁链方程、运动方程以及电磁转矩方程，其相关表达式如下[10]：

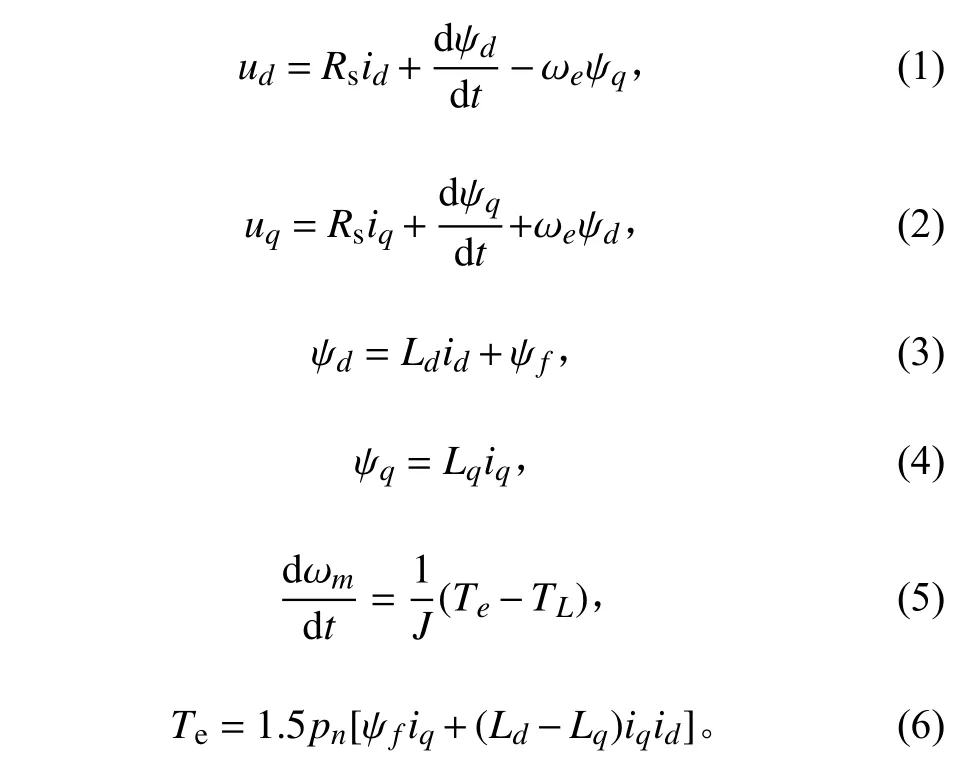
式中：ud，uq为定子电压的dq 轴分量；Rs为定子电阻；id，iq为定子电流的dq 轴分量；ψd，ψq为磁链的dq 轴分量；ωe为电机电角速度；ψf为永磁体磁链；Ld，Lq为直轴和交轴电感；J 为转动惯量；ωm为机械转速；TL为负载转矩；Te为电磁转矩；pn为磁极对数。

1.2 逆变器建模

1.3 船桨模型建模

船舶在航行过程中，依靠推进电机带动螺旋桨旋转而产生的推力，在克服海水对螺旋桨产生阻力矩的基础上，若剩余推力方向与船舶航行方向一致，则推动船舶加速前进，当剩余推力为0 时，船速稳定。依据螺旋桨的基本原理[11]可得直线航行时四象限船桨数学模型为：

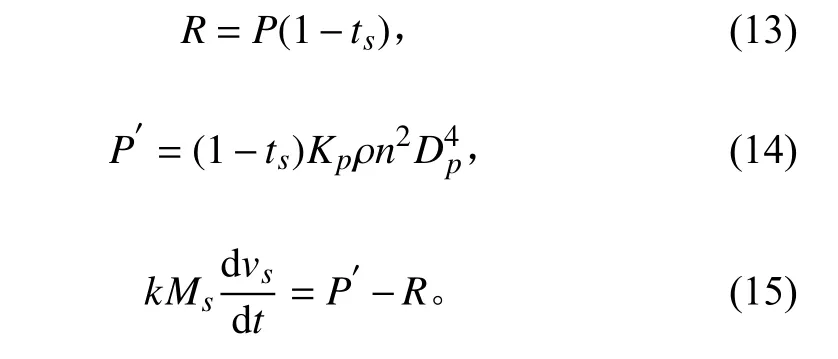
式中：P，TL分别为螺旋桨旋转时产生的推力以及阻力矩；ρ 为海水密度；n 为螺旋桨转速；DP为螺旋桨直径；Kp为螺旋桨推力的无因次系数；Km为螺旋桨阻力矩的无因次系数；vp为桨相对水的轴向速度；hp为桨回转一周的的轴向进程，Jp为定义轴向进程与轴向速度的比值为进速比；w 为伴流系数；vp为螺旋桨进速；P 为螺旋桨总推力；R 为船舶所受的阻力；ΔP 为推力减额；其中，若推力减额系数ts已知的话，可根据式（13）计算阻力。

综上所述，简化以后的船舶推进电机运动控制系统如图2 所示[12]。

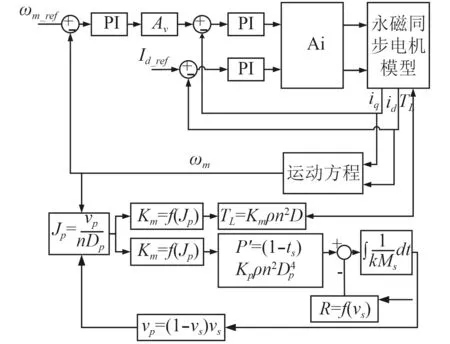
图2 系统简框图Fig.2 The simplified block diagram of system

2 永磁同步电机电压方程数值求解

2.1 数值解法分析

由上述式（1）和式（2）可知，电机电压方程为一组常微分方程组。虽然常微分方程的解法有多种，但就电机这种具有非线性、强耦合特点的特殊系统来说，由于经常遇到操作及故障，因此一般不采用无法自起步、需要多于一步的状态量历史信息的多步法进行数值求解工作，而是选择可以自起步，即可以通过稳态值出发进行下一步数值求解工作的单步法。此外，在求解常微分方程组的过程当中，数值稳定性将是决定能否采用这种方法的重要考量因素。而所谓数值稳定性，是指在计算过程中前一步形成的误差在后续时步计算中是否收敛，若收敛，则数值稳定。

对设特征根为λ，计算步长为h 的一阶微分方程进行不同单步法下的数值稳定性分析。计算真值与实际计算机得到的值之间有误差，将相邻两次误差之间比值称之为此方法的误差传递规律。在误差比值的绝对值小于1 的判定条件下，得到每种方法的数值稳定域。由表1 计算可得知，梯形法的数值稳定域为整个左半平面。当λ＜0 时，即系统稳定，无论步长为何值，hλ 均小于0，位于数值稳定域内，方法的计算误差都能收敛，结果不会发生畸变，。而当λ＞0 时，无论步长为何值，hλ 均大于0，即系统无法稳定。这使得在实际计算中，不会误得“系统稳定”的结果[13]。同理可知，其他几种单步法在数值稳定性方面均没有梯形法好。

表1 常用单步法误差传递规律Tab.1 The error transfer law of common single-step methods

2.2 数值求解

利用梯形法[14]离散dq 轴电机电压微分方程：

式（16）表示梯形法离散的表达式，式（17）表示式（16）中的f1，f2，式（18）则表示整体化简后的表达式。

利用牛顿-拉夫逊法差分后的方程为一组非线性方程，其求解步骤如下：

本研究旨在应用3%高渗盐水联合支气管扩张剂治疗毛细支气管炎患儿，观察其临床症状、肺功能的改善、住院时间及血清白介素-6、弹性蛋白酶水平变化，评估高渗盐水的疗效，同时探讨其可能的作用机制，为治疗毛细支气管炎寻求一种安全、有效、经济的治疗方法。

步骤1设定迭代次数变量k，而id（t）和iq（t）为t 时刻的未知变量。当牛顿迭代程序运行时，此时，迭代次数k=1，id（t-1）和iq（t-1）为ikd（t）和ikq（t）的初值。

步骤2根据牛顿迭代法的公式计算求解非线性方程组Jacobean 矩阵：

步骤3计算两次迭代电流之间的误差值。

步骤4若某次迭代电流的误差值小于一个设置的精度值ε，则中止迭代，输出上次迭代的电流值。

步骤5输出的电流计算公式如下：

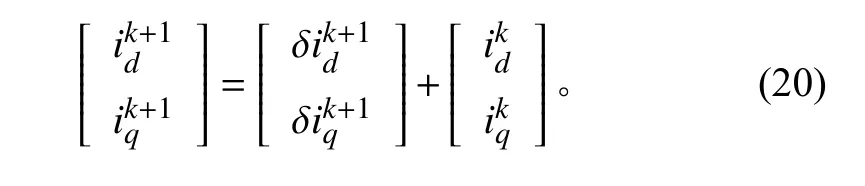
步骤6若迭代次数k 大于预设的最大迭代值，迭代程序结束并输出ikd（t）和ikq（t），否则回到步骤2进行新的一轮迭代。

3 仿真实验分析

3.1 电机数值仿真

本文以中铁渤海铁路渡轮1 号船舶[15]为仿真对象，基于Matlab R2014a 平台，搭建该船电机矢量控制系统仿真模型，对其进行不同数值解法的恒负载运行仿真实验,以此来模拟出电机从静止启动直到给定转速运行的状态。其中，仿真时间为5 s，给定恒负载为1 000 N，电机步长为5*10-5s 给定转速为120 rad/s。实验所用电机相关参数如表2 所示。

由图3 可以看出，在dq 轴下搭建的永磁同步电机模型中，q 轴的电压电流在经历过PI 调节后迅速达到恒定。与此同时，图3（d）中的转矩也达到恒定。由此可见，dq 轴下电机搭建的模型与实际契合。图3（c）为各种算法下的电机转速曲线。其中，在求解电机差分方程时均为牛顿法，区别在于微分方程的离散方法不同。可以看出，虽然每种方法都能很快达到转速稳定，但是相对而言，前进欧拉法相较于其他几种方法波动较大。在起步时刻，梯形法响应速度较其他方法更快。虽然梯形法的超调相较于其他2 种方法更大，但是仍属于正常范围内。在达到转速稳定期间，梯形法相较于其他方法优势很明显。因此，梯形法离散加牛顿法求解更适用于电机差分化后方程组。

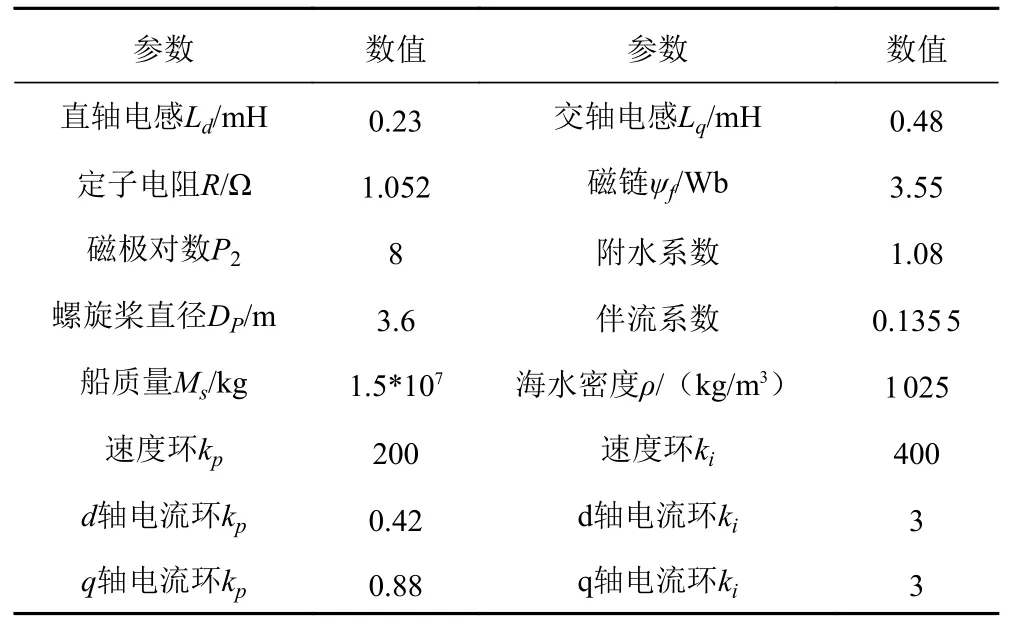
表2 电机参数Tab.2 simulated motor parameters

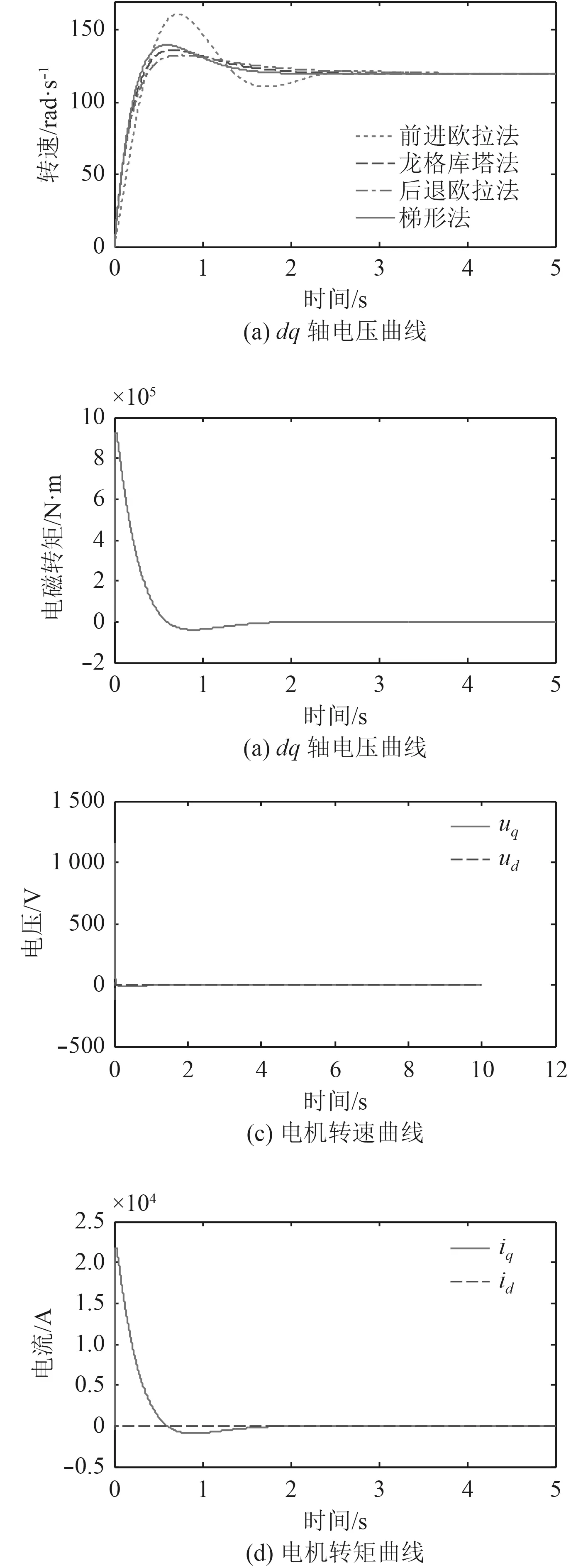
图3 恒转矩下的电机部分变量曲线Fig.3 Partial variable curves of motor under constant torque

3.2 船机桨负载仿真

由于Kp和Km是在螺旋桨敞水试验中，通过曲线拟合得到其与进速比Jp之间的关系，表3 为螺旋桨敞水特性曲线上不同的离散点。

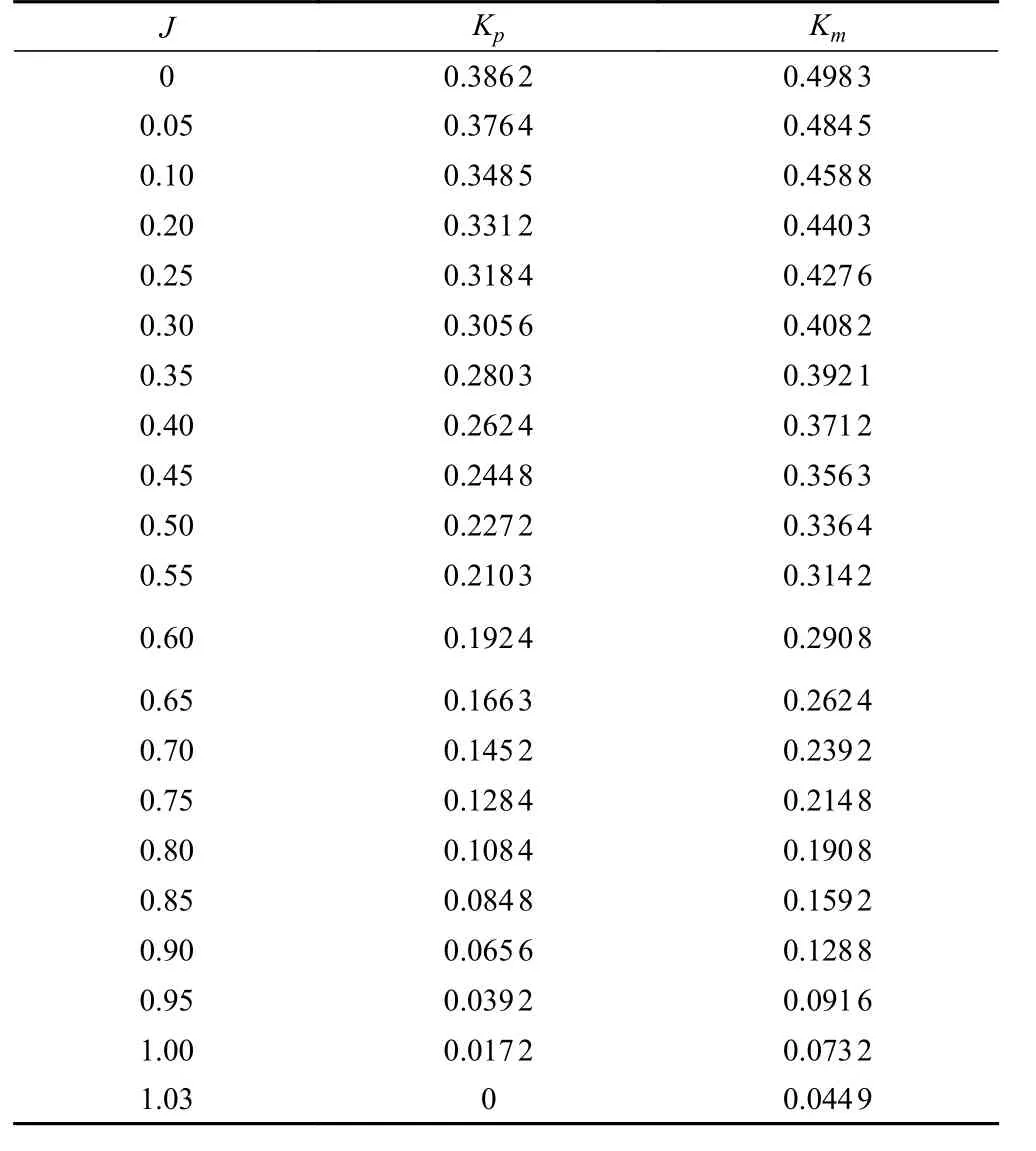
表3 螺旋桨趟水特性Tab.3 The propeller open water characteristic

利用Matlab 内置函数polyfit 进行2 阶多项式曲线拟合，所得函数中的每项系数取4 位有效数字。

文献[16]给出了中铁渤海铁路轮渡1 号船舶在某几个船速下船舶受到阻力的详细计算结果，如表4所示。

表4 烟大渡轮船舶阻力计算Tab.4 Calculation the ship resistance of Yantai-Dalian train ferry

与上述计算过程同理，得到拟合后的函数表达式如下：

至此，可利用上述算法以及船机桨数学模型来分析船舶在不同工况下的动态响应。

船舶启航操作一般可以分为直接启动和分级启动2 种方式。

1）直接启动

船舶从零速状态下起车到达额定转速的的操作叫做正车。其正车时的船舶航速vs、螺旋桨负载转矩TL、螺旋桨转速vp如图4 所示。当电机开始工作时，螺旋桨转速和船舶航速迅速达到稳定，其中螺旋桨转速在大约5 s 时开始达到稳定状态，如图4（c）所示。而螺旋桨转矩则经历了达到峰值后随即降低的过程，在500 s 左右时达到稳定。图4（a）和图4（b）对比可知，当螺旋桨转矩上升时，船速也随之上升，而在螺旋桨转矩下降初期，船速仍处于上升期，直到螺旋桨转矩稳定时，此时船速恒定。由此可以得出结论，当船舶以额定转矩直接启动，在船舶加速的过程中，推进电机的转矩过载。

2）分级启动

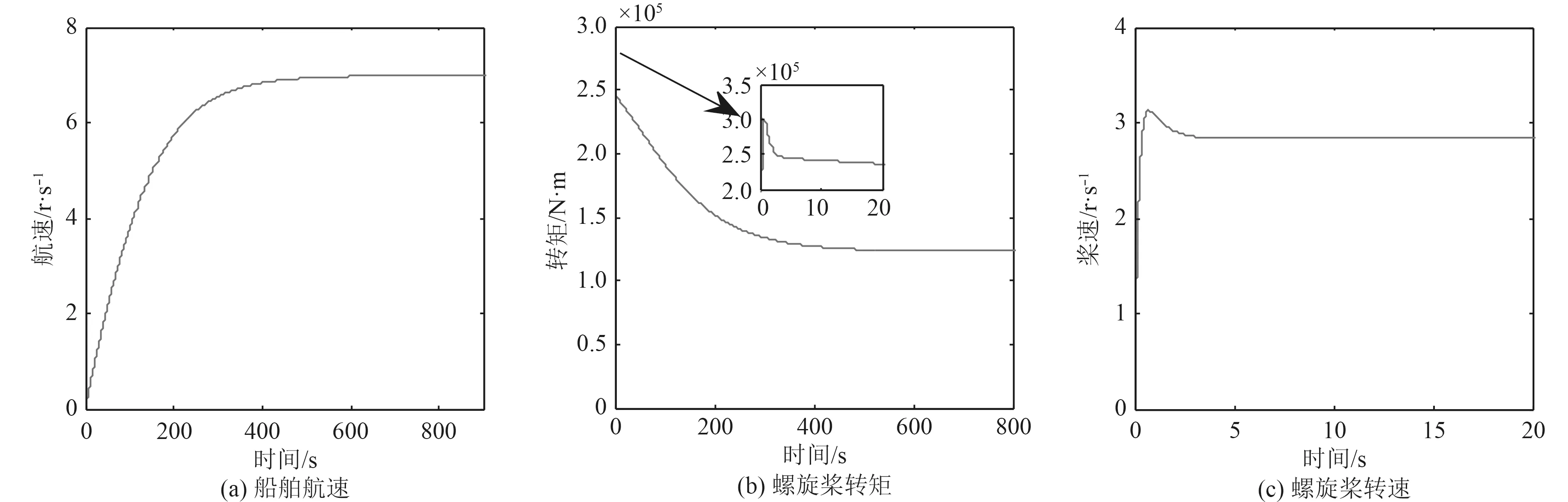
图4 直接启动Fig.4 Direct start

图5 分级启动Fig.5 Stepped starting

为了避免推进电机转矩过载而导致的设备损坏，在实际船舶正车当中，一般选择分级启动。本文仿真实验，分级启动分为3 个阶段，即通过阶段性地提高船舶转矩，使得船舶航速阶段性地稳定，从而达到预定航速，其船舶航速vs、螺旋桨转矩TL、螺旋桨转速vp如图5 所示。当船舶进行第1 级启动时，此时船舶处于加速阶段，而船舶负载转矩处于较小阶段，船舶约在800 s 时达到此级的稳定转速，随后进行下一级启动。在图5（b）可以看出，在每次级别启动的时刻螺旋桨转矩都有一次突变，随后又稳定在与螺旋桨转速相对应的转矩值上。在整个启动过程中，螺旋桨转矩的峰值约在170 kN，与直接启动中图4（b）相比，大大减小了推进电机的转矩，也减小了事故发生的概率或维护成本。同时，从图5（a）和图5（b）可以看出，分级启动的所用时间比直接启动所用时间更长。

4 结 语

本文在dq 轴下搭建永磁同步电机矢量控制简化模型，通过船机桨之间的基本特性分析，结合螺旋桨敞水特性曲线以及实例船舶阻力计算，利用全代码的方式实现了船舶推进电机运动控制系统的仿真。电机数值仿真实验结果验证了牛顿加梯形法相较于其他方法，更适用于求解差分化的永磁同步电机电压微分方程组。在船舶推进电机运动控制系统仿真当中，不同工况下船机桨的动态响应也证明了该模型具有可行性。本文建立的数学模型及相应数值仿真解法可为后续研究提供理论基础。