基于CT图像的Al/PTFE反应材料冲击压缩行为的三维细观模拟研究
2020-10-27杨相礼王传婷
杨相礼,何 勇,何 源,王传婷,周 杰,徐 涛
(1.南京理工大学 智能弹药技术国防重点学科实验室,江苏 南京 210094;2. 湖北航天飞行器研究所,湖北 武汉 430040)
引 言
反应材料(Reactive Materials)又称反应金属材料,由反应材料制备的含能毁伤元在高速侵彻目标的同时,释放大量的化学能量,对目标造成动能与化学能双重毁伤。相比于炸药和推进剂等传统的含能材料,反应材料具有更高的能量密度和机械强度[1-2]。由于其广泛的军事应用前景,以铝/聚四氟乙烯(Al/PTFE)为代表的反应材料近年来受到了广泛的研究。
Davis等[3]于1960年首次在专利中提出了Al/PTFE反应材料的制备工艺,徐松林、阳世清[4-6]、赵鹏铎等[7]对Al/PTFE反应材料的制备工艺、力学性能等进行了广泛地研究。张先锋[8]、任会兰等[9]分别研究了W含量对Al/PTFE/W反应材料准静态、动态压缩性能的影响。王海福等[1,10]用二次撞击释能的方法研究了3种不同金属聚合物的活性破片的冲击释能行为,并开展了活性破片对煤油油箱的引燃试验。周杰等[11]通过改变金属钨(W)的含量,金属铝(Al)与聚四氟乙烯(PTFE)的粒径,研究了材料配比与颗粒粒径对反应材料准静态压缩性能与冲击释能特性的影响。
上述研究成果均是在宏观层面对Al/PTFE类反应材料的力学行为和冲击反应行为进行的研究。然而,越来越多的研究表明,反应材料在细观尺度上的颗粒形状、粒度级配、内部缺陷等都对反应材料的力学性能和反应行为有重要的影响;而现有的理论和试验手段在研究细观尺度行为对宏观响应的影响上有一定的局限性。针对上述问题,一些学者将多尺度有限元方法应用到反应材料的研究中:乔良等[12]采用随机投放的方法建立了满足金属颗粒粒径统计规律的Al/PTFE/W反应材料细观有限元模型;葛超等[13]基于材料的真实细观特性统计规律,建立了Al/PTFE反应材料的细观力学模型。然而上述研究均将Al/PTFE反应材料中的铝颗粒假设为圆形(球形),未考虑材料颗粒的真实形状,这与材料的实际情况差距较大。
针对上述情况,本研究采用理论与数值模拟相结合的方法研究了Al/PTFE反应材料的细观冲击压缩行为。基于三项式物态方程和混合物叠加原理,计算了Al/PTFE反应材料的冲击Hugoniot关系;采用纳米CT获得了Al/PTFE反应材料的三维细观图像,并采用数字图像处理技术和网格映射方法,建立了与细观图像较为一致的三维细观有限元模型,研究了Al/PTFE反应材料的细观冲击响应及金属颗粒变形行为;结合物态方程计算结果和细观冲击压力场,研究了反应材料的细观冲击温度分布,以期为Al/PTFE反应材料的冲击反应行为研究提供参考。
1 基于三项式的冲击物态方程
1.1 冷能项和点阵项
反应材料在强冲击作用下,其组分受到冲击波强烈的压缩作用并最终发生化学反应,根据反应起始时刻的不同,可将化学反应分为冲击诱发化学反应(SICR)和冲击辅助化学反应(SACR)。反应材料的冲击物态方程是研究反应材料冲击反应行为的重要手段。本研究根据混合物叠加原理[14],基于三项式物态方程,计算密实态Al/PTFE反应材料的冲击物态方程。
三项式物态方程主要包括冷能部分、点阵部分和电子部分[15],其能量方程和压强方程分别为:
E(V,T)=Ec(V)+En(V,T)+Ee(V,T)
(1)
P(V,T)=Pc(V)+Pn(V,T)+Pe(V,T)
(2)
式中:下标c、n、e分别表示冷能项、点阵项和电子项。在冲击温度低于104K时,可忽略电子项的影响。
采用Born-Mayer势描述材料的冷能和冷压:
(3)
Pc(V)=Qδ2/3{exp[q(1-δ-1/3)]-δ2/3}
(4)
式中:δ为压缩度,δ=ρ/ρ0K=V0K/V;V0K为零温比容;γ(V)为Grüneisen系数,其可表示为:
(5)
式中:Q,q为冷能参数,可由解析方法求得:
(6)
(7)
式中:冷能参数c0K、s0K和ρ0K均为零温零压下的材料参数,可通过对常温下获取的材料参数c0、s进行零温修正获取,修正的解析方法为:
(8)
(9)
根据Debye点阵理论,金属或高分子的晶格热压和点阵热均可表示为:
(10)
(11)
(12)
式中:M为摩尔质量;Rg为摩尔气体常数,其值为8.314J·mol-1·K-1;D(x)为Debye函数;ΘD为Debye特征温度,对于大多数材料,ΘD≈100~500K,比定容热容可由式(13)计算:
(13)
(14)
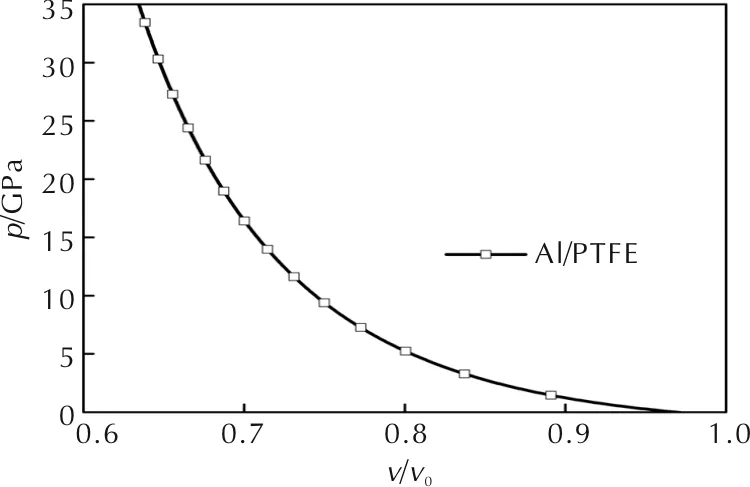
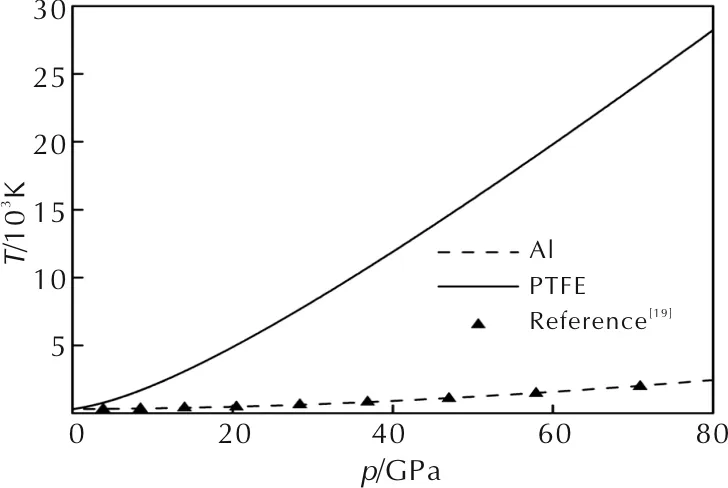
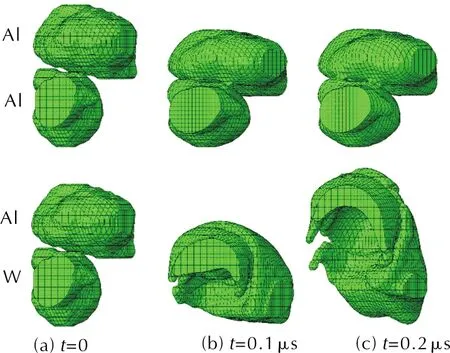
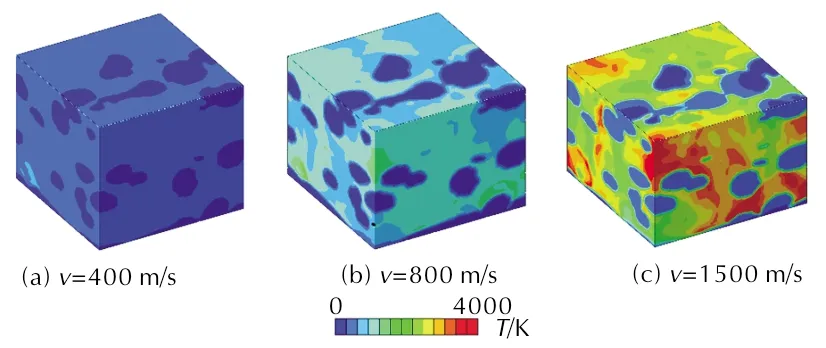
在温度T0 (15) fD(x)≈1-0.01x-0.04x2 (16) 混合物的各物理参量采用质量平均混合法则处理,按照质量平均叠加原理,混合物的比容V和冷能Ec可由下式计算: (17) (18) 式中:n为组分数量;mi为第i组分的质量分数;Vi和Eci分别为第i组分的比容和冷能。 根据上述理论模型计算的Al/PTFE反应材料的冲击Hugoniot关系曲线如图1所示,由三项式物态方程计算出的单质材料冲击温升曲线如图2所示,其中铝的冲击温升计算结果与参考文献[17]计算结果吻合较好。计算所需参数见表1。 表1 物态方程计算相关参数[16] 图1 Al/PTFE反应材料冲击Hugoniot的关系曲线Fig.1 The calculated Hugoniot curves of Al/PTFE reactive material under shock loading 图2 铝与聚四氟乙烯单质冲击温升曲线Fig.2 The calculated pressure—temperature curves of single Al and PTFE 从图2可知,随着压力的增大,PTFE材料的冲击温度急剧升高,远高于Al材料的冲击温度。 本研究考虑建立零氧平衡的Al/PTFE(26.5/73.5)反应材料的真实细观数值模型,材料铝颗粒粒径为75μm,聚四氟乙烯粒径为25μm。材料的制备过程采用文献[11]的方法,主要包括混合、压制、烧结等。考虑到设备分辨率和射线穿透能力,将烧结后的材料研磨至尺寸近似为2mm×2mm×5mm的长立方体,使用纳米CT设备(蔡司Xradia510)对试件进行三维扫描,获得像素尺寸为2μm的系列细观图像。为了建立材料的细观模型,从获得的细观图像中选取0.4mm×0.4mm×0.4mm的区域(ROI)[18]。采用最佳阈值方法(Otsu method)对数字图像进行阈值分割,灰度值高于阈值的部分为Al颗粒,其余为PTFE基体;由于本研究制备的反应材料具有很高的密实度(大于99%),从CT照片上仅能发现极为少量的缺陷,故忽略材料的空隙。图像进行阈值分割前需要进行平滑处理等增强措施,使用图像开运算和闭运算对阈值分割后的图像进行处理,填补空洞和光滑边界。最后采用映射算法将材料属性映射入模型网格,模型网格尺寸为4μm。Al/PTFE反应材料的典型CT图像及图像处理流程如图3所示,其中图3(c)中绿色区域为铝颗粒,灰色区域为PTFE基体。 通过上述的图像处理及网格映射方法,建立了如图4所示尺寸为0.4mm×0.4mm×0.4mm的三维有限元模型,模型中Al颗粒与PTFE基体的体积比为22/78,接近Al/PTFE反应材料的组成配比(22.25/77.75)。模型中的冲击波由模型上方沿Z轴方向以恒定速度V运动的质量块产生;与Z轴平行的侧面设置为滑移边界,以消除侧向稀疏波的影响。 图3 Al/PTFE反应材料的CT图像及图像处理示意图Fig.3 The CT image and the image processing instruction of Al/PTFE materials 图4 Al/PTFE反应材料细观有限元模型Fig.4 Mmeso-scale finite element model of Al/PTFE reactive material PTFE与Al的强度方程均采Johnson-Cook 强度模型[19],状态方程采用Mie-Grüneisen 状态方程,相关参数见表1和表2。质量块采用Al材料模型。由于冲击压缩过程中,材料发生较大的变形,本模型采用多物质欧拉算法描述材料的变形行为;在欧拉算法中,模型的网格节点保持不动,材料的状态参数则随材料的流动在网格节点间传递,该方法适合描述高速撞击情况下材料的大变形行为。 表2 Al、PTFE与W材料Johnson-Cook强度模型参数[20-21] 由于材料细观尺度上的异质性,为了获得冲击Hugoniot模拟结果,沿冲击方向上选取靠近模型两端的两单元层如图4所示,将每层10000个单元模拟结果的平均值作为该截面上的冲击Hugoniot结果。当撞击速度为v=800m/s时,两层单元的平均压力曲线如图5所示,图中层2曲线的卸载是由于冲击波到达模型底部自由边界后的反向卸载。沿曲线的压力上升沿做平行线,两平行线间的距离即为冲击波在层间的传播时间Δt,则可由层间距L计算出冲击波速度us,而冲击压力p与粒子速度up则分别可由两组压力曲线与粒子速度曲线上升沿峰值的平均值得到。由此,可直接获得Al/PTFE反应材料的up—us关系与up—p关系。 图5 名义撞击速度为800m/s时两个单元层的 压力—时间曲线Fig.5 The pressure—time curves of the two element layers under nominal impact velocity of 800m/s 为研究不同冲击压力情况下材料的冲击响应行为,分别模拟了名义撞击速度在200~1500m/s范围内Al/PTFE反应材料的细观冲击响应行为。按上述结果计算方法,计算冲击压力p、粒子速度up与冲击波速us的模拟结果,并与理论计算结果及参考文献的试验结果[22]对比如图6所示。由图6可知,理论计算结果略微高于数值模拟和试验结果。其中,本研究的理论与数值模拟up—p关系与实验结果吻合较好,表明了本研究所建立的细观数值模型的正确性;而up—us曲线在低速段与实验结果存在较大的差异,分析可能由于理论与数值模型中忽略了材料的细观空隙及实验测量误差带来的差异。 图6 Al/PTFE反应材料冲击Hugoniot关系理论与 模拟结果对比Fig. 6 Comparison of impact Hugoniot relation between theoretical and numerical results 名义撞击速度为1500m/s时,材料在撞击开始后0.02、0.04、0.08μs3个时刻的冲击压力分布与颗粒的变形情况如图7所示。图8则绘出了3个不同撞击速度下,撞击时刻分别为0.004、0.02、0.04、0.08μs4个瞬时,沿撞击方向(Z轴)的各层单元压力均值,反映了该瞬时材料的波形。 图7 名义撞击速度1500m/s时Al/PTFE反应材料 细观压力分布和Al颗粒变形情况Fig.7 Meso-scale pressure contours and deformation of Al granules in Al/PTFE reactive material under nominal impact velocity of 1500m/s 由图7可知,由于冲击阻抗的差异,冲击波在铝颗粒中传播更快,引起波阵面的弯曲,Al/PTFE反应材料中的冲击波在细观尺度上并不能形成平整的波阵面,但图8所示某一瞬时的平均波形基本保持不变,证明本研究所选的模型尺寸能正确反应材料的宏观响应。与均质材料所不同的是,冲击波阵面掠过后,反应材料并未立即达到压力均匀状态,由于阻抗的差异,Al颗粒中的瞬时压力低于PTFE基体中的压力,并随着加载的持续而逐渐达到平衡。 Thadhani等[23-26]对Al/Ni粉末反应材料的研究认为,冲击波作用下反应的发生与材料颗粒尺度的力学行为有密切的关系。与Al/Ni反应材料在冲击波作用下铝镍颗粒发生的强烈变形与材料混合不同,由于Al与PTFE材料的塑性差异较大,冲击波压缩引起的塑性变形主要集中在PTFE基体中;铝颗粒在冲击波的作用下,主要表现为空间上的位移和沿冲击波传播方向上的体积压缩,Al颗粒与PTFE基体并未发生剧烈的互相混合。 图8 名义撞击速度分别为400、800和1500m/s时, 4个不同时刻材料中的瞬时平均压力波形Fig.8 Average pressure profile at four transients under nominal impact velocity of 400,800 and 1500m/s 为了提高Al/PTFE反应材料的机械强度和反应性能,常将一定量的W加入到反应材料中。为深入分析Al颗粒的变形情况和W的加入在细观尺度上的影响,从模型中取出2个铝颗粒作为研究对象,设置较长的PTFE基体以加载更长的冲击波;并将其中一个颗粒赋予W的材料属性。当其中一个颗粒的材料属性分别为Al和W,名义撞击速度为1500m/s时,金属颗粒的变形过程如图9所示。 图9 名义撞击速度为1500m/s时Al-Al、Al-W颗粒的 相互作用及变形情况Fig.9 The interaction and deformation of Al-Al and Al-W particles under nominal impact velocity of 1500m/s 由图9可以看出,在冲击波作用下,铝颗粒受到冲击波的压缩作用,沿冲击方向受到压缩并互相接近,但基本形状并未发生改变;而由于W颗粒有更高的阻抗,在同等冲击波作用下粒子速度较低,铝颗粒追赶上W颗粒并与之发生碰撞,两颗粒的形状发生剧烈的变化,两种情况的差异与乔良[12]的二维数值模拟结果一致。W颗粒的加入,促进了与之相邻的Al颗粒的变形及与PTFE基体的混合,同时W颗粒与铝颗粒的塑性变形产生额外的温升,起到促进形成反应热点的作用。 Zhang X. F等[27]认为,反应材料的细观冲击温升与材料的反应效率有密切的关系。根据上述的物态方程计算结果,不同的冲击压力和材料具有不同的冲击温度;又因为在冲击波加载的时间尺度内,可以忽略材料的热传递,认为材料处于绝热状态;根据数值模拟的压力场和材料压力—温度曲线计算的材料细观冲击温度场如图10所示。与理论模型假设的材料温度均匀分布不同,撞击速度越大,材料的温升越高,冲击波阵面掠过后,材料细观尺度上的压力仍未达到平衡状态,细观温度场呈不均匀分布状态。 图10 名义撞击速度分别为400、800和1500m/s时 Al/PTFE反应材料细观冲击温度场Fig.10 Meso-scale shock temperature contours of Al/PTFE reactive material under nominal impact velocity of 400, 800 and 1500m/s 由图2单质材料冲击温升的计算结果,同等冲击压力下,PTFE的冲击温升远高于Al的冲击温升。对于某一撞击速度,其波阵面后的温度场呈温度较低的铝颗粒嵌在温度很高的PTFE基体中的状态,两者的温度差异随冲击强度的增大而增大。需要指出的是,本研究计算的冲击物态方程并未考虑冲击熔化,因此未考虑熔化潜热对冲击温升的影响。常压状态下,铝材料的熔点为933K,作为有机高分子材料,通常认为PTFE的熔点为600K,温度高于773K时,发生较为明显的热分解,释放出活性分子[28]。 (1)基于三项式物态方程和混合叠加准则的理论计算结果与基于真实图像的三维细观数值模型的冲击Hugoniot计算结果一致,并于试验数据吻合较好,验证了理论与数值模型的正确性。 (2)由于Al与PTFE材料的冲击阻抗的差异,波阵面后材料并未立即达到细观尺度上的压力平衡状态。较大的塑性差异使Al颗粒与PTFE基体两种组分没有发生明显的相互混合。W颗粒的加入促进了与之相邻的Al颗粒的变形,在材料中起到形成反应热点的作用。 (3)在不考虑冲击熔化潜热的情况下,根据Al材料和PTFE材料的冲击温升理论计算结果和数值模拟压力场,计算了反应材料的冲击温度场,波后温度场呈温度较低的Al颗粒嵌在温度较高的PTFE基体中的状态。1.2 混合物叠加原理
1.3 计算结果

2 数值模拟
2.1 图像处理和网格划分
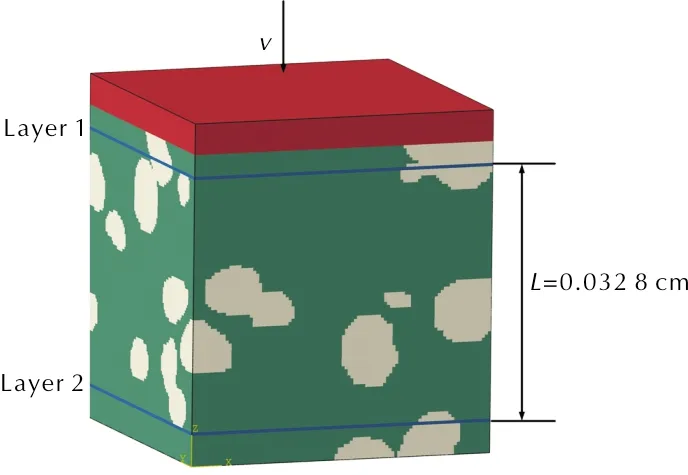
2.2 有限元模型


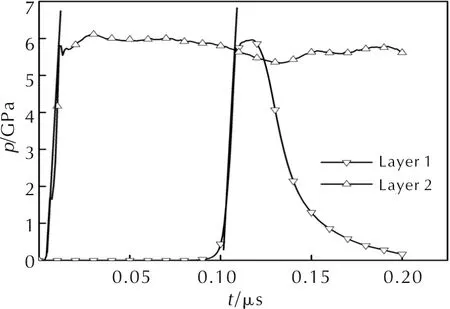
2.3 计算结果处理方法
3 结果与讨论
3.1 冲击Hugoniot关系


3.2 细观压力分布与颗粒变形行为


3.3 冲击压缩细观温度场
4 结 论
