四轴飞行器的建模与仿真分析
2020-10-26廖干洲


摘要:四轴飞行器具有可以垂直升降、任意角度灵活移动等特点,并且可以在其机身上搭载不同的器件,如摄像头、机械手臂等进行功能拓展。现在理想条件下建立了四轴飞行器的动力学模型,从飞行位置和飞行姿态方面反解四轴电机的实际转速,并通过PD算法控制提高飞行器控制速率,使用Matlab软件对其进行了仿真。仿真结果表明,该四轴飞行器在理想状态下能达到精确控制的效果。
关键词:四轴飞行器;动力学模型;位置控制;姿态控制
0 引言
四旋翼飞行器也被称为四轴飞行器,是一种有4个螺旋桨的飞行器,其螺旋桨分布分为2种类型,分别为十字型和交叉型。此类飞行器可以灵活地实现各种飞行模式,如爬升、悬停、滚转、俯仰等。相对于传统的固定翼飞行器,四轴飞行器可以实现更多的飞行动作,并且在制作成本、体积以及控制简易性上都有无可比拟的优势。当下四轴飞行器成了一个研究热点,除了实验室研究以外,一般的工科大学生或者电子设计爱好者都可以以较低的价格设计完成一个四轴飞行器。
1 坐标系的建立
想要设计四轴飞行器,首先要对其进行动力学建模,为了得到飞行器的数学模型,首先必须根据地面和机体建立2个不同的坐标系,分别为以地面为基础的地理坐标系和以飞行器本身为基础的机体坐标系。
1.1 地理坐标系
地理坐标系O相对于地球表面不动,取东北天方向建立该坐标系,取固定点作为原点,e1、e2、e3分别为一般意义上的x、y、z轴,如图1所示。
1.2 机体坐标系
机体坐标系B与飞行器联系,对于交叉型飞行器来讲,坐标原点为飞行器的质心,ox指向1、4号电机的角平分线,规定此方向为正方向;oy指向1、2号电机的角平分线;oz垂直于oxy平面,符合右手法则。
1.3 机体机械结构
四轴飞行器按照电机的分布类型不同,可分为十字型结构以及交叉型结构,如图2所示。这2种结构对于控制系统仿真来讲区别不大,由于考虑到“X”结构在市面上的应用比较广泛,参考资料也比较多,本文统一针对“X”结构进行讲解。
2 飞行角度
四旋翼飞行器的飞行姿态可以用3个角度表示,分别是翻滚角φ、俯仰角θ、偏航角ψ。
四旋翼飞行器飞行姿态的3种欧拉角示意图如图3所示。翻滚角φ(Roll Angle)是沿着翻滚轴(Roll Axis),也就是ox轴转动的角度,从机体后方往前看,记右转为正方向,反之为负方向。俯仰角θ(Pitch Angle)是沿着俯仰轴(Pitch Axis),也就是oy轴转动的角度,从左方往右看,记右转为正方向,反之为负方向。偏航角ψ(Yaw Angle)是沿着偏航轴(Yaw Axis),也就是oz轴转动的角度,从机体上方往下看,记右转为正方向,反之为负方向。
以上得到的动力学模型,是在假设的理想条件下得到的简化模型,故在实际应用中有较大的局限性。对四轴动力学模型进行简化,是为了减小后面进行仿真计算的难度,在初步的理论研究中可以接受四轴动力学简化模型。
4 飞行位置控制系统设计
四轴飞行器的控制包括姿态控制和位置控制,它们之间有直接的联系。为了控制四轴的位置,必须控制飞行姿态。
飞行器控制系统具有2个控制回路,为内、外控制回路结构。外控制回路负责控制飞行器的位置,位置控制决定了飞行器能否准确到达目标位置;内控制回路负责控制飞行器的飞行姿态,姿态控制决定飞行器飞行运动过程中的稳定性。
飞行器控制系统结构框图如图4所示。
外控制回路根据给定的目标位置,通过式(8)反解出飞行需要的姿态角(φ,θ,ψ)和垂直输入控制量u1。内控制回路根据以上得到的姿态角和垂直输入控制量,进一步反解出角度输入控制量u2、u3、u4。通过式(8)最终得出4个控制量u1、u2、u3、u4,然后再通过式(7)得到每一个旋翼的上升力Fi,i={1,2,3,4}最终根据电机和浆翼的参数得出每一个电机的转速n1,i={1,2,3,4}控制四轴飞行器实现期望的飞行位置以及飞行姿态。
5 Matlab仿真
本文利用Matlab软件搭建四轴飞行控制系统仿真模型,对其进行仿真研究,由于未进行实物测量,直接选取一组模拟的飞行器参数,如表1所示。
本文在Matlab中进行仿真,以所建立的数学模型在Matlab中构建仿真回路,仿真模型主要由位置控制模块、姿态控制模块、姿态反解模块和位置反解模块组成,考虑到控制的复杂性,所有的控制模块都采用PD控制方式,如图3所示。
令世界坐标系下,坐标原点O为{0,0,0},考虑到飞行控制器的4个控制量分别为飞行器高度、翻滚角度、俯仰角度和偏航角度,飞行器的初始条件可记为(zinit,φinit,θinit,ψinit),目标条件可记为(zdes,φdes,θdes,ψdes),通过软件仿真得到高度坐标的响应曲线以及3个角度的相应曲线。
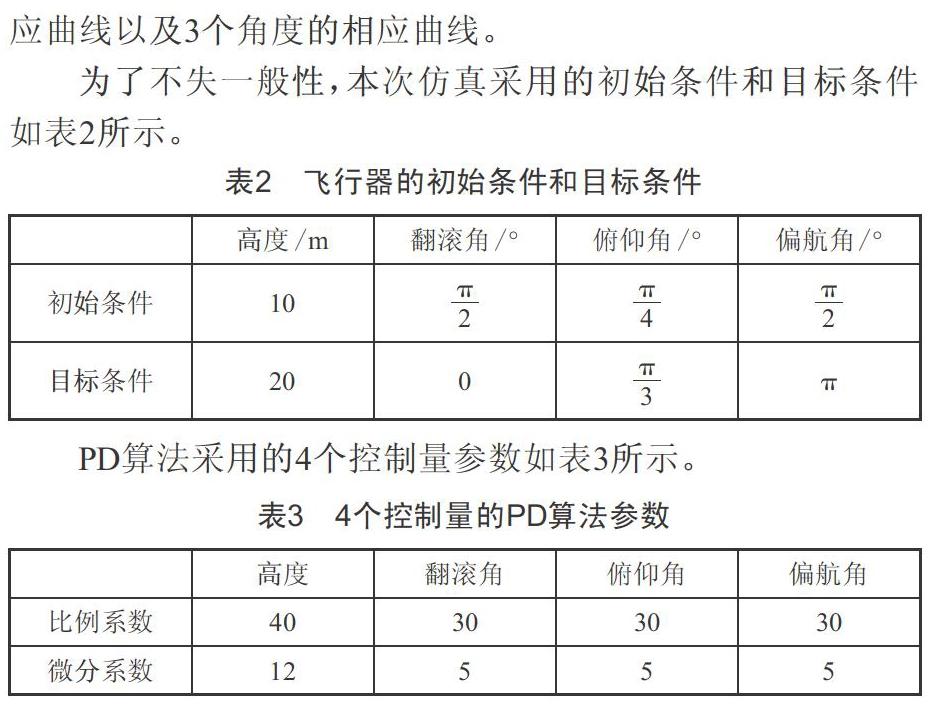
为了不失一般性,本次仿真采用的初始条件和目标条件如表2所示。
PD算法采用的4个控制量参数如表3所示。
图5(a)为应用PD算法得到的3个欧拉角的响应曲线,为内反馈的姿态控制单元。图5(b)为高度位置的响应曲线,为外反馈的位置控制单元。为了明显区别4条曲线,翻转角、俯仰角、偏航角、高度的初始响应时间分别为1 s、2 s、3 s、4 s。通过曲线可以看到,4个控制量的稳态误差为0,说明应用PD算法的四轴能在大概1 s内平稳实现目标姿态,到达目标位置。
6 结语
本文根据四轴飞行器的原理,建立了理想状态下的四轴飞行器动力学模型。四轴飞行器在控制方面,采用了位置控制以及姿态控制的双回路控制方法以及PD算法,并在Matlab平台下对其进行了仿真。根据仿真结果可知,该四轴飞行器在理想状态下能达到精确控制的效果。设计人员后续通过添加对于实际大气状态的仿真条件,进一步整定PD算法的参数等,为四轴飞行器的实际制作奠定基础。
[参考文献]
[1] 聂博文,马宏绪,王剑,等.微小型四旋翼飞行器的研究现状与关键技术[J].电光与控制,2007,14(6):113-117.
[2] 庞庆霈.四旋翼飞行器设计与稳定控制研究[D].合肥:中国科学技术大学,2011.
[3] 杨庆华,宋召青,时磊.四旋翼飞行器建模、控制与仿真[J].海军航空工程学院学报,2009,24(5):499-502.
[4] 王秀萍,張天光.捷联惯性导航技术[M].北京:国防工业出版杜,2007.
[5] 程学功.四轴飞行器的设计与研究[D].杭州:杭州电子科技大学,2012.
[6] 胡三庆.基于MEMS加速度传感器的空间运动轨迹追踪系统设计与实现[D].武汉:华中科技大学,2009.
[7] 李素敏,王杰,宋北光.一种改进的PID控制算法[J].微计算机信息,2006,22(25):40-41.
收稿日期:2020-09-08
作者简介:廖干洲(1983—),男,广东人,工学硕士,讲师,研究方向:机器学习、控制技术。
