自回归移动平均模型在全国流行性腮腺炎发病数预测中的应用

惠石生　马莹　尚成英　杜瑞

摘要：目的：应用自回归移动平均模型预测全国流行性腮腺炎月发病数。方法：运用Eviews 8.0软件对2013年10月至2018年10月的腮腺炎发病数构建乘积季节ARIMA模型，以2018年11月至2019年10月的数据作为检验样本，对模型的预测效果进行检验，再用所建模型预测2019年11月至2020年10月的全国腮腺炎月发病数。结果：通过对序列的平稳化、模型的识别、建立和诊断，建立ARIMA（3，1，2）x（l，1，1）12模型，该模型拟合效果显示，调整的R2为0.905，AIC值为-3.920，预测值与实际值的平均绝对误差为-561例，平均相对误差为4.59%。结论：ARIMA（3，1，2）x（1，1，1）12模型能较好地拟合全国腮腺炎月发病数的变化趋势，可用于我国腮腺炎的短期预测和动态分析。

关键词：流行性腮腺炎;自回归移动平均模型;预测

中图分类号：R512.1

文献标志码：A

流行性腮腺炎（Mumps）简称腮腺炎，是由腮腺炎病毒感染引起的一种急性呼吸道传染病，多发于儿童和青少年，很容易在学校和托幼机构中暴发/流行，会产生较大的社会影响[1，2]。本病患者临床表现较轻，部分患者可伴随或单独发生脑膜炎、胰腺炎、睾丸炎或卵巢炎等，严重者甚至致残或死亡，发病后尚无特效的治疗药物，当前对其防控的最有效手段是免疫接种[3]。据蒋蕊鞠等人研究发现[4]，2004年- 2018年全国共报告腮腺炎病例4 272 368例，年平均报告发病率为21.44/10万，且在麻疹一腮腺炎一风疹联合减毒活疫苗纳入免疫规划前后腮腺炎报告发病率无明显变化。另外本病暴发疫情较多，年暴发疫情事件数始终排在39种法定传染病的第1位，腮腺炎暴发疫情在我国依然较为严重[5]。因此对其发病数预测便显得十分重要。本研究采用季节性差分自回归移动平均模型（ AutoregressiveIntegrated Moving Average Model，ARIMA模型）对全国腮腺炎月发病数预测效果进行分析，观察其预测效果，得出结论。

1 资料与方法

1.1 资料来源

全国腮腺炎月发病数数据来源于中国疾病预防控制中心网站中关于“法定传染病报告”数据，收集时间从2013年10月至2019年10月，数据收集地区为全国31个省市自治区（不含香港、澳门特别行政区和台湾地区）。病例类型包括临床诊断病例和实验室确诊病例。

1.2 ARIMA模型基本思想

自回归积分滑动平均模型是由Box和Jenkins于20世纪70年代初提出的一种时间序列预测方法。而季节性ARIMA模型是ARIMA模型中最高级的一种，它充分考虑了时间序列的趋势性和季节性变化，并将影响传染病发生的社会、医学、自然等各种因素的综合效应统一蕴涵于时间变量中进行分析，短期预测的准确性较好。

1.3 ARIMA模型建模过程

标准的SARIMA模型为ARIMA（p，d，q）X（P，D，Q）s，其中p.d、q分别表示非季节性自回归阶数、差分阶数和移动平均阶数，P、D、Q分别表示季节性自回归阶数、差分阶数和移动平均阶数，S表示季节性周期。乘积季节ARIMA模型的建立包括序列的平稳化处理、模型的识别、参数估计和检验、模型的诊断检验和模型预测五步。其中模型平稳化处理包括差分和数据转换等方式，而参数估计采用最小二乘法或极大似然法进行，再应用模型决定系数平稳R2、贝叶斯准则（SBC）等对初步选定的模型进行评价，其中R2越大越好，AIC值越小模型越好，采用Box-Ljung Q检验法对选定模型残差是否为白噪声进行检验，若Q值对应的P>0.05，提示是白噪声序列;模型的预测包括模型的拟合效果验证和预测。

1.4 统计学分析方法

首先用Excel 2003软件建立数据库，以月为时间单位汇总2013年10月至2019年10月腮腺炎的发病数，采用Eviews 8.0软件进行ARIMA模型的建立和预测，其中以2013年10月到2018年10月的腮腺炎发病数建立备选模型，以2018年11月至2019年10月的数据作为检验样本，检验模型的预测精确度，最后运用最优模型预测2019年11月至2020年10月的腮腺炎月发病数。

2 结果

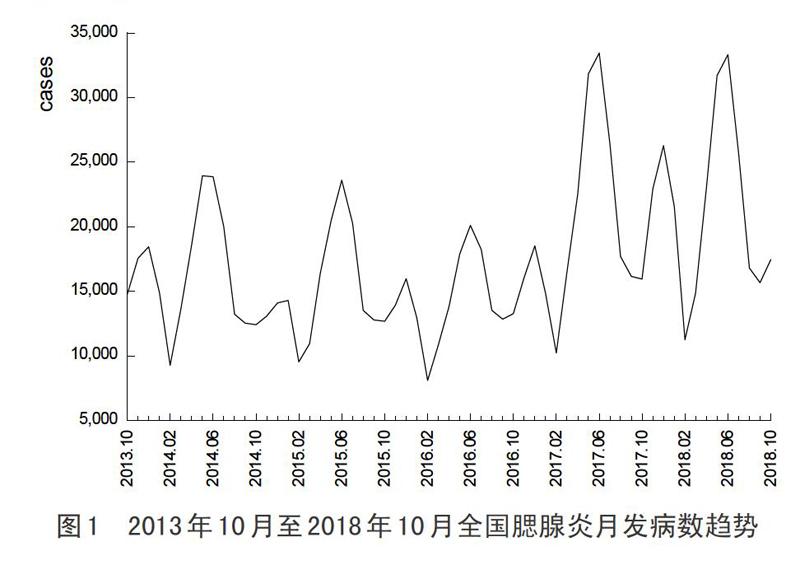
2.1 2013年10月至2018年10月全国腮腺炎月发病数趋势

从图1可以看出该序列无离群点和缺失值，从2013年10月至2018年10月全国腮腺炎月发病数波动较大，具有明显的季节性周期，表现为每年的4月～7月和11月～次年1月两个发病高峰，说明该序列具有周期性季节特点，是不平稳的时间序列，需要对其进行平稳化处理。

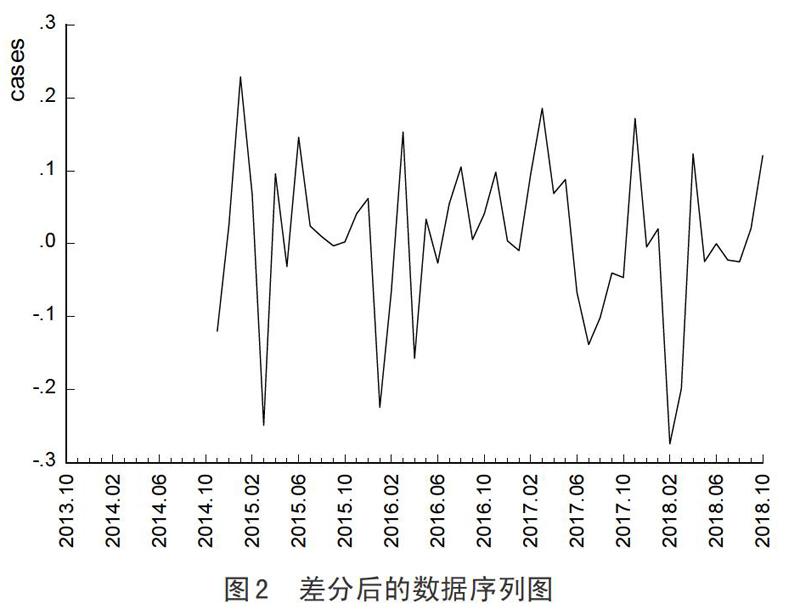
2.2 序列的平稳化处理与检验

首先对数据进行了一次自然对数转换，使该序列的方差平稳下来，再进行一次非季节性差分和一次季节性差分，之后观察处理后的序列图（如图2所示）。从图2可以看出，差分后的序列虽然仍有些波动，但其均值基本在0上下摆动，之后又对差分后的数据序列采用ADF检验法进行单位根检验，发现ADF检验的统计量t=-6.493，P=O.OOO，说明经过变换后的序列平稳，可以进行建模。

2.3 模型定阶及建立

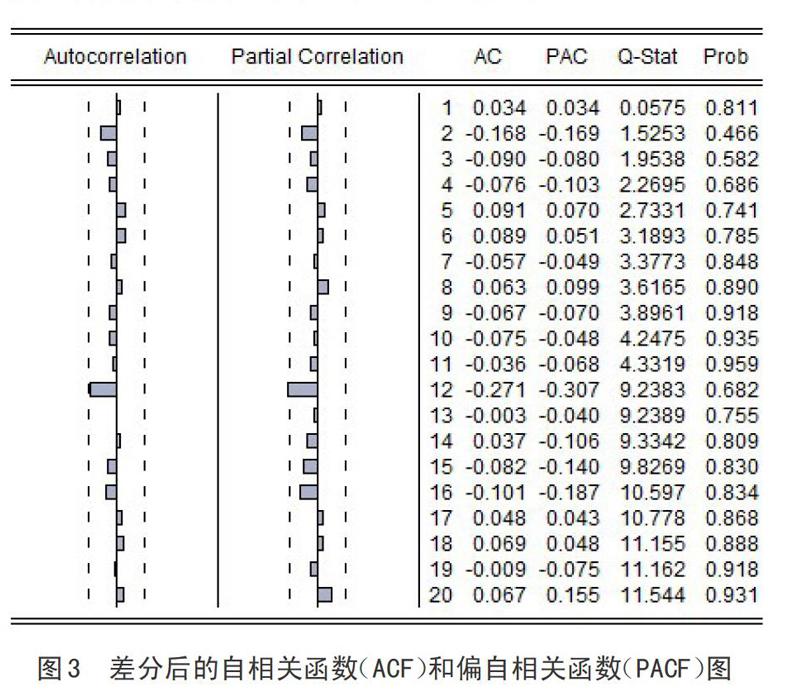
2.3.1 模型定阶

由于本次研究首先对原始数列进行了一次非季节性差分和一次季节性差分，所以初选模型为ARIMA（p，1，q）X（P，l，Q）12，然后对差分后的自相关函数（ACF）图和偏自相关函数（PACF）图（如图3所示）进行观察，并根据简洁原则，使得所建模型对数据的收集、处理及过多参数带来的干扰和误差最不敏感，来确定模型参數[6]。本次研究选取p和q的取值范围为1-3，从低阶至高阶逐一进行试验。另外根据《现代医学统计学》（方积乾，陆盈，人民卫生出版社，2002）的介绍[7]，P和Q超过2阶的情况很少见，故本研究对P和Q分别取0，1，2进行逐个试验，根据模型的参数及模型总体的显著性、拟合优度等进行比较，选择最佳模型。

[2]汤健闻，柳智豪，我国流行性腮腺炎流行概况及其免疫预防[J].微生物学免疫学进展，2015，43（3）：51-57.

[3]朱洪坤.流行性腮腺炎46例的流行病学及临床特征分析[J].中华传染病杂志，2014，32（ 11）：690-691.

[4]蒋蕊鞠，殷琼洲，徐明珏，等.2004 - 2018年全国流行性腮腺炎发病特征及重点防控人群分析[J].中国当代儿科杂志，2019，21（5）：441-444.

[5]钟贵良，林希建，刘姝.2008-2012年长沙市流行性腮腺炎流行病学特征分析[J]中华疾病控制杂志，2014，18（2）：120-122.

[6]李欣阳，李素娟，刘晓迪，等，自回归移动平均乘积季节模型在甲型肝炎发病数中的应用[J].山东大学学报（医学版）， 2018， 56（12）： 103-108.

[7]方积乾，陆盈.现代医学统计学[M].北京：人民卫生出版社，2002.

[8]费方荣，冯录召，许真，等.2008-2010年中国流行性腮腺炎流行病学特征分析[J].疾病监测，2011，26（9）：691- 693.

[9] Zamir CS. Schroeder H，Shoob H，et al.Characteristics of alarge mumps outbreak： clinical severity， Complications andassociation with vaccination status of mumps outbreak cases[J]. Hum Vacc.in Immunother， 2015， 11（6）：1413-1417.

[10]惠石生，陳立章，刘富强，等.乘积季节自回归积分滑动平均模型在流行性腮腺炎发病率预测中的应用[J].中华预防医学杂志，2015，49（12）：1042-1046.

[11]沈忠周，马帅，曲翌敏，等.ARIMA模型在我国法定传染病报告数中的应用[J].中华流行病学杂志，2017，38（12）：1708-1712.

[12]胡咏梅，郝利新，王华庆.中国2010 - 2012年流行性腮腺炎流行病学特征分析[J]。中国疫苗和免疫，2014，20（2）：127-131.

[13]言晨绮，王瑞白，刘海灿，等.RIMA模型预测2018-2019年我国肺结核发病趋势的应用[J].中华流行病学杂志，2019，40（6）：633-637.

[14]杨小兵，汪鹏，江高峰.ARIMA乘积季节模型在流行性腮腺炎发病率预测中的应用[J].公共卫生与预防医学，2013，24（6）：39-42.

[15]石雷.细菌性痢疾月发病率ARIMA季节模型预测分析[J].中国公共卫生，2014，30（9）：1234-1235.

作者简介：惠石生（1987-），男，回族，甘肃平凉人，硕士，讲师，主要从事流行病与卫生统计学研究。