基于Copula-Bayesian组合模型的长江干线水上交通安全风险概率评估

刘清 张娟

（武汉理工大学交通学院，湖北 武汉 430063）

【摘 要】 为提高长江干线水上交通安全风险防控能力，针对现有水上安全风险分析模型的局限性，提出Copula-Bayesian組合模型研究长江干线全航段水上交通风险分布规律，计算各分布点的主要事故概率。研究结果表明，在下游沙洲水道樊口施3号红浮附近水域最容易发生碰撞事故，在中游芦家河水道芦家河6号红浮附近水域发生搁浅事故可能性最高，在上游猪儿碛水道石板坡桥右1号红浮附近水域触礁事故分布概率最大，在上游江津水道江津桥右1号红浮附近水域船舶自沉事故较多。研究结果可为海事部门有针对性地开展安全防范工作提供参考。

【关键词】 长江干线;通航安全;Copula-Bayesian组合模型;分布概率;风险防范

0 引 言

长江航运是长江经济带综合交通运输体系的重要组成部分，长江航运安全是长江经济带发展的重要保障。2018年长江干线货船平均吨位由2017年的1 630 t提升至1 780 t，船舶大型化对航道通过能力提出更高的要求。随着长江南京以下12.5 m深水航道贯通并投入试运行，5万吨级海船已能直达南京港，万吨级江海船舶可常年直达武汉港，武汉至重庆段可通航5 000吨级单船和万吨级船队。长江上中下游常年维护水深相差较大，枯水期航道水位明显降低，使得长江上中游搁浅风险增多。2018年长江干线年货物通过量达到26.9亿t，较2017年增长7.6%，货运量增长致使船舶密度加大，船舶碰撞、触礁事故时有发生。为适应长江航运船舶日益大型化、航道通过能力显著提高和货物通过量稳步增长等发展趋势，对新形势下长江干线水上交通安全风险进行研究具有新的意义，可提高长江干线水上交通安全风险防控能力，着力防范和化解重大风险。

目前水上安全风险研究颇受关注，国内外学者常用贝叶斯（Bayesian）单一模型对水上安全风险进行研究，由于水上交通事故样本少，难以获得稳定的测算结果，容易造成结果失真。针对现有研究不足，提出在SPSS软件相关性检验基础上利用Copula模型验证Bayesian网络各节点间的相互关系，构建Copula-Bayesian组合模型来解决长江干线水上交通安全风险分布问题。研究长江干线全航段水上各种交通事故高发点的分布规律，有助于海事部门了解不同航段应重点关注的风险类型，更具针对性地辨识船舶通航风险源，从而制定符合长江干线水上交通安全实际的风险防范策略。

1 长江干线水上交通安全现状与影响因素

1.1 安全现状

长江干线航道上起云南水富港，下至长江入海口，全长 km。2018年，长江干线共发生运输船舶等级事故27件，死亡失踪35人，沉船19艘，直接经济损失万元，同比分别下降5.2%、20.4%、5%和39.2%。长江航运安全形势总体保持稳定，但部分重点水域典型事故仍时有发生。

重点分析2008―2018年期间长江干线水上交通事故发现：在事故发生时间方面，夜间发生事故较多，且发生时间集中在零点到早晨6点之间;在事故发生航段方面，相比宜宾合江门（上游里程 km）至武汉长江大桥（中游里程2.5 km）航段，武汉长江大桥（中游里程2.5 km）至浏河口（下游里程25.4 km）航段水上交通事故数量更多;在事故类型方面，长江干线以碰撞、搁浅、触礁、自沉、火灾、风灾等事故为主;在事故成因方面，包括船员操作不当、疏忽大意、装载不当、违反航路规则等人为因素，船舶主舵机故障、链缆断裂、线路故障等船舶因素，大雾、雷雨、暴风雪等天气因素和航道条件、水流、交通流等航道因素。

1.2 影响因素

长江干线水上交通安全系统是一个由“人-船-环境-管理”组成的复杂系统，任何一个环节出错都可能导致事故发生。根据事故致因“2-4”链式模型可将水上交通事故分为内部原因和外部原因两个层面，直接原因、间接原因、根本原因和根源原因等4个阶段，其中：直接原因是船员的不安全行为、船舶的不安全状态和通航环境的不安全条件;间接原因是船员的安全意识不足、安全习惯不佳、风险防范不到位等;根本原因是长江干线水上交通安全管理体系不健全;根源原因是长江干线水上交通相关管理部门安全文化的缺失。以上直接原因由间接原因引起，间接原因由根本原因引起，根本原因由根源原因引起，最终导致事故的发生往往是直接原因。由此总结出影响长江干线水上交通安全的主要因素有人为因素、船舶类型、航道宽度、航道水深、水流和航道能见度等。

（1）人为因素：船员的心理、生理和行为能力会对船舶正常航行造成影响。当船员情绪急躁、身体疲劳时，其操作能力低、应急能力弱，这时更容易发生事故。

（2）船舶类型：长江干线客渡船、客滚船、高速客船、旅游船、危险品船等“四客一危”船舶是长江航运的核心，很多航段经常对“四客一危”船舶进行安全检查，能有效预防交通事故的发生。然而，运砂船多存在超吃水、配员不足、证件不齐、不配合海事部门检查等违规问题，影响其他船舶安全航行和航道秩序，存在严重的安全隐患。

（3）航道宽度：船舶在航行、避让、调头时都需要一定的水域空间。充足的水域空间的基础是航道宽度够宽，狭窄的航道浪损岸吸现象非常普遍，会对船舶操纵造成影响，导致船舶偏离正常航道，易发生搁浅、触礁等事故。航道过窄，两船避让不当，也容易引发碰撞事故，对通航安全造成影响。

（4）航道水深：随着长江干线船舶大型化，船舶吃水也越来越深，船舶航行时要充分考虑船底与水底的安全距离。船舶在浅水中航行，周围水流加速，容易导致船舶下沉和纵倾加剧，前进阻力增加，舵效不良，操纵困难，容易发生触礁、搁浅、船体倾斜等事故。

（5）水流：丰水期水流流速较快，流态紊乱，重载上行船舶航行困难，极易因间距不足、操纵困难而发生碰撞、触礁等事故。枯水期水浅槽窄，船舶航行更加困难，浅窄航段通航安全存在隐患，易发生搁浅、触损等事故。

（6）航道能见度：遇夜间或大雾天气，航道能见度降低，船员视线受限，视距不足，无法准确瞭望前方航道和观察过往船舶的情况而及时作出判断。当船员发现险情时通常已经错过最佳避险时机，往往来不及改变船舶航向和航速，从而造成水上交通事故。

2 长江干线水上交通安全Copula -Bayesian组合模型的构建

2.1 选择研究方法

由概率和数理统计理论可知，多元变量之间的相互关系可用分布函数表示，但变量联合分布函数形式复杂，不利于求解。Copula函数是刻画变量非正态、非对称、非线性等相关关系的统计工具，具有连接变量间联合分布函数与其各自的边缘分布函数的功能，开辟了更方便获取联合分布函数的途径，可以很好地解决变量之间的关联性问题。Bayesian网络模型主要是基于概率分析和图论的一种不确定性知识表达和推理模型，能在不完整或不确定的信息条件下利用随机变量间的关系，通过条件概率表进行学习和推理。Copula-Bayesian组合模型兼有Copula模型和Bayesian网络的优点，在利用Copula模型准确描述各因素之间相关性的同时，依据Bayesian网络对分布概率进行推断，以获得稳定的测算结果。

由于长江干线水上交通事故影响因素较多并且各影响因素之间呈非线性关系，其相互关系难以判定;因此，本文采用Copula-Bayesian组合模型对长江干线水上交通安全风险进行研究。

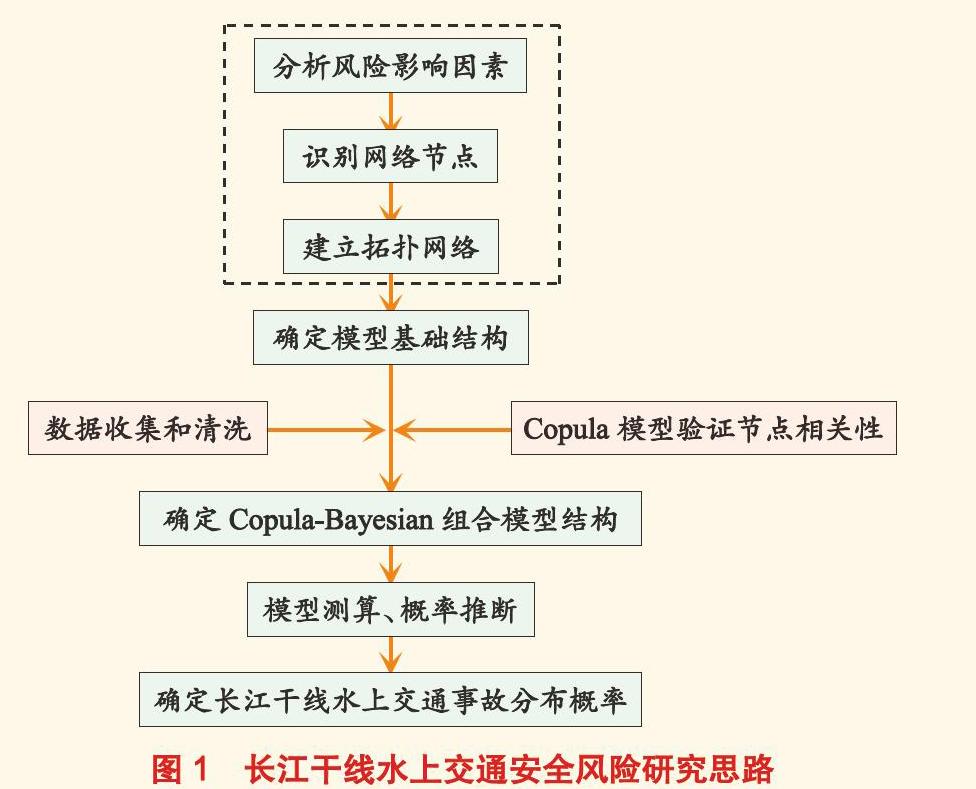
研究思路是先通过分析长江干线水上交通安全风险影响因素来确定建模的各节点，构建模型基础结构;再利用Copula模型验证各节点之间的相互关系，确定Copula-Bayesian组合模型拓扑结构;最后借助GeNIe软件测算模型，进行概率推断，确定网络中各节点的概率分布，得出整个长江干线水上交通事故分布概率（见图1）。

2.2 构建模型

详细分析长江干线水上交通安全风险的影响因素，是确定Copula-Bayesian组合模型节点的依据和基础。依据指标体系的建立原则，经过对比分析，最终选取事故类型y作为目标节点，船舶类型x1、航道宽度x2、航道水深x3、水流x4、航道能见度x5和事故发生航段x6作为证据节点。分析长江干线事故险情数据（见表1），各节点的主要参数（见表2）。

借助SPSS软件对各节点参数作肯德尔（Kend-all）相关性分析，得到各节点间两两相关的显著性结果，再结合相关专家知识，确定各节点间的相互关系，从而构建长江干线水上交通安全风险模型的基本网络结构。各节点相关性检验结果见表3。

3 长江干线水上交通安全风险 概率测算

据长江海事机构统计，2008―2018年长江干线共发生626起事故过程描述全面的水上交通事故，归纳整理得到626组完整数据用于模型测算。

3.1 数据清洗

由于水上交通事故数据存在数据漂移及不确定性，随着时间推移会对测算结果产生影响，需对水上交通事故数据中的异常数据进行清洗。水上交通事故异常数据的清洗一般采用物理判别的方法，通常有格拉布斯准则法、肖维勒准则法、拉依达准则法和狄克逊准则法等4种。对比这4种方法，拉依达准则法适用于数据样本较大的情况，且操作简单、使用方便、准确性高，因此此次研究采用拉依达准则法进行数据清洗。

以拉依达准则法为基础算法对水上交通事故数据进行处理，其原理是用事故数据的3倍标准差3 作为取舍依据：当| xi x |>3 ，则xi为异常数据，应予剔除;当| xi x |≤3 ，则xi为正常值，应该保留（xi为样本容量中第i个数据的值，为样本容量的算术平均值）。

对全部统计数据进行清洗后可知，包含异常数据的个案共20组，其中涉及到的参数有“航道宽度”节点中的“≥500 m”，“事故发生航段”节点中的“长江下游里程0～100 km”“长江下游里程100～200 km”“长江下游里程200～300 km”“长江下游里程300～400 km”和“長江下游里程1000～1100 km”，将这些数据予以剔除后，剩下606组数据用于模型测算。

3.2 Copula-Bayesian组合模型测算

在长江干线水上交通安全风险基本模型结构基础上，利用Copula模型对清洗后的数据样本进行相关性分析，建立各节点之间的联合分布函数，验证结构中各节点之间的依赖关系。多元正态Copula模型的分布函数及其与Kendall相关系数之间的关系如下：

C=4C（y，x1，x2，…，x6;）

dC（y，x1，x2，…，x6;） 1（1）

其中： C（y，x1，x2，…，x6;）=… exp dy dx1 dx2 … dx6（2）

式中：为已知Kendall相关系数; 为两两节点间的相关系数矩阵（见表4）。

注：标有“*”表示节点之间有显著相关性，各节点相互关系与所建基本模型结构一致。

计算各子节点条件概率，计算公式为

P（y | x1，x2，…，x6）= P（y | xi）（3）

航道水深：

P（x3=1），P（x3=2），…，P（x3=8）（4）

航道宽度：

P（x2=1 | x3=1），  P（x2=2 | x3=1），…，  P（x2=4 | x3=1），…， P（x2=1 | x3=2），…， P（x2=4 | x3=8）（5）

事故发生航段：

P（x6=10 | x3=1，x2=1），  P（x6=11 | x1=1，x3=1），…，P（x6=39 | x3=8，x2=4）（6）

船舶类型：

P（x1=10 | x3=1，x6=10），  P（x1=2 | x3=1，x6=10），…， P（x1=9 | x3=8，x6=39）（7）

航道能见度：

P（x5=1 | x3=1，x6=10），  P（x5=2 | x3=1，x6=10），  P（x5=1 | x3=2，x6=10），…， P（x5=2 | x3=8，x6=39）（8）

航道水流：

P（x4=1 | x2=1，x6=10），  P（x4=2 | x2=1，x6=10），  P（x4=1 | x2=2，x6=10），…， P（x4=2 | x2=4，x6=39）（9）

该模型后验概率的计算公式为

P（y | x1，x2，…，x6）=P（y =1 | x1=1，x2=1，…，x6=1） + P（y =1 | x1=1，x2=1，…，x6=2） + … + P（y =10 | x1=9，x2=4，…，x6=22）（10）

根据式（3）～（10）计算Copula-Bayesian风险模型的分布概率。篇幅有限，仅列出在水深为3.2～4.5 m、航道宽度为200～300 m、事故发生航段在长江下游里程900～1 000 km、事故发生在能见度小于1 000 m等4个约束条件下，不同水流条件和船舶类型的事故类型节点条件概率分布（见表5）。

借助GeNIe软件训练Copula-Bayesian组合模型，对长江干线水上交通安全风险分布进行推理分析，训练成功后的模型结构见图2。

图2显示出了船舶类型、航道宽度、水深、水流、航道能见度和事故发生航段对事故类型的推理结果：“事故类型”节点中“碰撞”的后验分布值最大，为0.40，“搁浅”的后验分布值为0.26，“触礁”的后验分布值为0.11，“自沉”的后验分布值为0.08，4种事故类型占总的事故类型的比重为0.85。在长江上游里程600～700 km猪儿碛水道、长江中游里程500～600 km芦家河水道、长江下游里程900～1 000 km沙洲水道，航道宽度为200～300 m、水深为2.9～3.2 m的航段事故分布概率较大，且主要发生在枯水期、能见度小于1 000 m时，发生事故的船舶绝大多数为散货船。

3.3 结果分析

为寻找长江干线事故多发的重点水域，辨识长江航道不同事故类型概率分布点，判断不同航段应重点关注的风险类型，列出碰撞、搁浅、触礁、自沉等4类主要事故类型分布航段及概率值，分别见图3、图4、图5、图6。

由图3可以看出，碰撞事故在长江中下游各个航段发生数量均较多，在长江下游沙洲水道樊口施3号红浮附近水域最有可能发生，其分布概率为0.15。该航段邻近武汉区段，有较多弯曲航道且两岸码头作业船舶多，船舶交通流量较大，船舶会遇几率增大，更易发生碰撞事故。

由图4可以看出，搁浅事故主要分布在长江中游航段，在长江中游芦家河水道芦家河6号红浮附近水域最有可能发生，其分布概率为0.16。中游水域浅滩分布广泛且覆盖面积较大，搁浅事故发生较多。

由图5可以看出，触礁事故主要分布在長江上游猪儿碛水道、江津水道和长江下游东北横水道附近水域，在长江上游猪儿碛水道石板坡桥右1号红浮附近水域最有可能发生，其分布概率为0.19。该水域位于重庆区段，重庆多山，大部分航段仍为山区自然航段，暗礁数较多，触礁事故分布大。

由图6可以看出，自沉事故相较其他三类事故发生较少，在长江上中下游分布相差不大，主要分布在长江上游江津水道、猪儿碛水道，长江中游邓家口水道和长江下游沙洲水道，在长江上游江津水道江津桥右1号红浮附近水域最有可能发生，其分布概率为0.10。该航段位于重庆区段，水流湍急、落差大，通航环境复杂，易受风浪影响，从而导致船舶沉没。

4 结 语

（1）构建Copula-Bayesian组合模型研究长江干线水上交通安全风险，利用拉依达准则法清洗原始数据，借助GeNIe软件测算模型，得到模型各节点的条件概率分布，计算长江干线水上交通事故分布概率。

（2）根据Copula-Bayesian组合模型测算结果列出长江干线水上交通事故概率分布，获得长江航运4种类型主要事故的概率分布情况。碰撞、搁浅、触礁和自沉等4种类型事故分别在长江下游沙洲水道樊口施3号红浮附近水域、长江中游芦家河水道芦家河6号红浮附近水域、长江上游猪儿碛水道石板坡桥右1号红浮附近水域和长江上游江津水道江津桥右1号红浮附近水域发生的可能性最大。

得到长江干线主要事故概率分布点，为下一步防范化解重点水域重大风险和制定风险防范策略提供参考，具有应用价值。