动态主动打断项目组合选择问题的模型研究

闫庆友， 王雅娴， 孙艺新

(1.华北电力大学 经济与管理学院,北京 102206; 2.国网经络技术研究院有限公司,北京 102209; 3.国网能源研究院有限公司,北京 102209)

0 引言

当今世界经济迅猛发展，企业的经营和融资领域不断扩大，为了提升企业核心竞争力并实现长远发展，选择性地执行若干项目成为一种有效的竞争机制。因此，如何从诸多的项目中选出收益最大的项目组合就显得至关重要，该类问题称为项目组合选择问题(Project Portfolio Selection Problem, PPSP)，即：决策者从一组有限的备选项目中选择一个项目组合，该项目组合不但要最大限度的实现组织目标，还要符合相应的资源约束限制[1]。1952年，Markowz[2]在金融投资领域中首次提出了投资组合的概念，这是项目组合的雏形。之后，Lorie和Savage[3]于1955年正式提出了项目组合选择问题，并将之应用到了企业项目管理中。自此，项目组合选择在多个领域得到了广泛的应用，如：研究与开发项目[4]、风险投资公司[5]、创新型企业[6]等。

根据项目是否可以打断执行，现有的项目组合选择问题可以分为可打断项目组合选择和不可打断项目组合选择两类[7]。不可打断是指：一个项目一旦开始，就必须连续执行直到终止；可打断是指：项目在执行的过程中，不需要连续执行，而是可以分阶段按比例地完成[8]。根据打断的不同情况，可打断项目组合选择问题可以分为被动打断和主动打断。所谓被动打断是指：项目在实际执行的过程中，遇到了不可避免的突发状况(如：资金链断裂、材料短缺、人才流失等)不得不中断。所谓主动打断是指：企业决策者在选择项目组合时，就对可能引起项目打断的因素进行了充分的考虑，因此在执行过程中主动安排项目分阶段、按比例地执行。被动打断常常会使企业效益降低[9]，而周密计划的主动打断却会增加企业的效益。因此，近年来，主动打断项目组合选择问题得到了深入的研究。例如：Li等[10]首次提出了主动打断项目组合选择理论，并说明被动打断会给企业带来消极影响；李星梅等[11]研究了基于主动打断的双目标项目组合选择模型；王雅娴等[12]分析了资源约束和依赖关系对主动打断项目组合选择的影响。本文的研究亦落实在主动打断项目组合选择问题上。

虽然项目组合选择研究已经有六十多年的历史，但是目前对企业已有旧项目进行研究的文献还很少，大部分研究者只考虑新项目的选择，而忽略了企业已有的项目。例如：白思俊等[13]构建了针对新项目的项目组合选择模型，用于优化战略目标，并分析了收益、资源和风险的相互影响关系；Carazo等[14]研究了团队决策情景下的项目组合选择问题，并没有考虑企业已有旧项目；Mohagheghi等[15]分析了基于不确定环境的高新技术项目组合选择模型，忽略了已有旧项目的影响。然而，Harel等[16]在2005年就将项目组合选择问题分为动态和静态项目组合，Harel等明确指出：动态项目组合选择既考虑新的备选项目，又考虑企业已有的旧项目；而静态项目组合选择只考虑新的备选项目。直到近几年，动态项目组合选择问题才开始得到重视。Huang等[17,18]在其发表的两篇文章中对动态项目组合选择进行了专门研究：一篇[17]针对动态项目组合选择问题的复杂性，提出了一种新的二进制粒子群算法；另一篇[18]给出了一个均值方差最优的模型并设计了一种新的遗传算法，来解决跨国动态项目组合选择问题。这两篇文章指出了传统静态项目组合选择研究的缺陷：只重视新项目的选择，而忽略了新、旧项目的统筹安排。在项目组合选择中，如果能对企业已有的项目进行适当的调整(如：更新、放弃等)，企业将会获得更大的收益。因此，本文将研究考虑企业已有旧项目的动态主动打断项目组合选择问题。

敏感性分析又称灵敏度分析，可以分析模型中不确定性参数变化情况对企业经济效益的影响程度，进而可以为企业风险防范提供依据[19,20]。在项目组合选择问题中，已有一些研究人员开展了敏感性分析的相关研究。例如：Hasuike等[21]在考虑投资者主体性的情景下，对投资领域的项目组合选择问题做了敏感性分析；Liesi Ö等[22]针对多属性项目组合选择问题，进行了敏感性分析，得出了项目组合受基准值影响的敏感程度；李星梅等[23]对可打断项目组合选择模型的参数进行了局部敏感性分析，进而得出了各个参数的敏感性排序。由上可知，在项目组合选择问题中进行敏感性分析是有其理论意义和实际价值的。然而，通过查阅相关文献发现：尚没有学者针对考虑企业已有旧项目的主动打断项目组合选择问题进行敏感性分析，关于这一问题的敏感性分析具有创新性。故本文将对动态主动打断项目组合选择线性模型进行局部敏感性分析。

在上述分析的基础上，本文构建了适合敏感性分析的动态主动打断项目组合选择新模型，并对该模型进行了局部敏感性分析。文章结构安排如下：第二节设置模型的参数及变量，介绍动态主动打断项目组合选择问题的三种情景；第三节构建动态主动打断项目组合选择新模型，对之进行线性化处理；第四节给出新模型的算例，利用GAMS/BARON求解，并进行局部敏感性分析；第五节对全文进行总结，提出需要进一步深入研究的问题。

1 模型介绍

考虑企业已有旧项目的动态主动打断项目组合选择问题涉及多个阶段和多种约束条件，相对复杂。为了便于理解，本部分将对文中涉及的参数和变量进行相关描述，并介绍动态项目组合选择问题的三种情景。

1.1 设置参数和变量

(1)输入参数

Φ表示企业已有旧项目和新项目的集合，假设n为企业已有旧项目的数量，|Φ|-n为新项目的数量，则项目j∈Φ，j=1,…,n…|Φ|,其中j=1,2,3,…,n表示企业已有旧项目，j=n+1,n+2,n+3,…|Φ|表示新项目；

T表示企业已有旧项目更新时期，为了便于讨论，假设企业已有旧项目的更新时间段均为T；

A表示计划投资期的集合，则计划投资的总期数可用|A|表示，t∈A,t=1,…,T,…,|A|,其中t表示计划投资期内的第t时间段；

ξ表示紧前关系的集合，即若(i,j)∈ξ，则表示直到项目i结束后，项目j才可以开始；

r表示市场利率；

N表示在整个计划期内可供选择项目的最大数量；

M表示在每个时间段内可供选择项目的最大数量；

K(t)表示在t时间段期初企业通过筹资活动从外部获得的可用于项目执行的资金，t=1,…,|A|；

bj表示整个项目j完成后的收益，j=1,…,|Φ|；

hj表示在第1阶段开始的时候就放弃企业已有旧项目j，并将之卖掉所获得的收益,j=1,…,n；

ejt表示已有旧项目j在t阶段进行升级所需的费用，j=1,…,n；

sj表示由于主动打断，新项目j每执行一部分需要用到的准备成本，j=n+1,…,|Φ|；

kj表示整个新项目j执行需要投入的资金，j=n+1,…,|Φ|；

αjt表示新项目j在t阶段的最小执行比例，j=n+1,…,|Φ|；

βjt表示新项目j在t阶段的最大执行比例，j=n+1,…,|Φ|；

φK表示参数K(t)的变动比例，φK(t)=ΔK(t)/K(t)；

φs表示参数sj的变动比例，φs=Δsj/sj；

φk表示参数kj的变动比例，φk=Δkj/kj；

φh表示参数hj的变动比例，φh=Δhj/hj。

φe表示参数ej的变动比例φe=Δej/ej。

(2)中间变量

Vj表示项目j在计划投资期内的净现值收益，，j=1,…,|Φ|；

Cj表示已有旧项目j的机会成本，j=1,…,n；

W1表示|Φ|-n个新项目在计划投资期内的总净现值收益；

号召抵制权威学术期刊的著名科学家并非Schekman一个人。 在2012年，著名英国数学家William Timothy Gowers 组织了一场针对荷兰Elsevier公司出版的《CELL》的抵制运动。 反对出版公司只顾商业利益而不顾学术传播的做法。

W2表示n个已有旧项目在计划投资期内的总净现值收益。

(3)决策变量

xjt表示介于0和1之间的实数，并且满足xjt∈0∪[αjt,βjt]，xjt=0时项目j不执行，xjt≠0时项目j执行，且其执行比例介于αjt和βjt之间，j=1,…,n,…|Φ|。

1.2 问题描述

为了最大限度的实现企业收益，在进行项目组合选择时，不但要引进新项目，还要考虑企业已有旧项目是否适应当下的经济环境和市场需求，并对旧项目进行合理的调整。根据参数设置可知，企业已有旧项目的数量为n个，新项目的数量为|Φ|-n个。无论是已有旧项目还是新项目，假设在其生命周期结束时都没有残值。下面，将分别计算新项目和已有旧项目在计划投资期内的净现值收益。

对于新项目j(j=n+1,…,|Φ|)而言，考虑主动打断的情况时，模型中涉及准备成本sj、投入资金kj以及收益bj，故|Φ|-n个新项目在计划投资期内所获得收益W1为:

(1)

对已有旧项目j(j=1,…,n)而言，本文假设其有三种调整方式，分别为：维持现状、放弃以及更新。已有旧项目j的初始投资和收益都发生在计划投资期以前，是沉没成本，对当下的项目组合选择不造成影响，不能重复考虑(注：在计划投资期以前就预留了已有旧项目j的准备成本，准备成本也不予考虑)。因此，已有旧项目的机会成本Cj(j=1,…,n)为从计划投资期期初到已有旧项目j生命周期截止的净现金值，其表达式:

(2)

根据已有旧项目的三种调整方法，下面将分别给出三种情景下企业已有旧项目净现值Vj(j=1,…,n)对应的求解公式。

情景1已有旧项目维持原状

此时zj=1,uj=0,Vj满足:

(3)

由公式(3)可知，在情景1下，企业已有旧项目在计划投资期内的净现值为0。故可知：当已有旧项目维持原状时，不会对当下的项目组合选择造成任何影响。这也是动态项目组合选择没有得到充分重视的原因。然而，大部分研究者都忽略了对已有旧项目的其它调整方式，例如更新和放弃。因此，不考虑企业已有旧项目的静态项目组合选择不够全面，也不能获得最高的投资收益。

情景2放弃已有旧项目

此zj=0时，这种情况下，通过出售项目的相关机器、生产线以及剩余库存，企业可以获得相应的收益hj，于是可得:

(4)

情景3更新已有旧项目

此时zj=1,uj=1，假设在更新时期1至时期内，项目的净现值受到更新施工的影响，会缩减；在T+1至|A|时期内，项目已经完成更新，并得到了升级，其收益会相应增加。令项目j(j=1,…,n)的缩减比例为p，增加比例为q，那么可得:

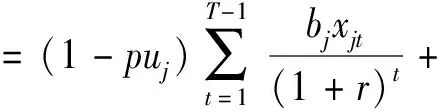
(5)

综合三个情景，由公式(3)～(5)可求得n个已有旧项目在整个计划投资期内的收益总和W2，如下式所示:

(6)

2 主动打断项目组合选择新模型

2.1 动态非线性模型

根据敏感性作用范围的不同，现有的敏感性分析方法可以分为两类，即：全局敏感性分析(多因素敏感性分析)和局部敏感性分析(单因素敏感性分析)。本文研究的动态主动打断项目组合选择问题涉及的参数和变量较多，全局敏感性分析对此类问题并不适用，可操作性弱。因此本文采用操作性强，易于求解且在实际中得到广泛应用的局部敏感性分析。此外，由于各参数值往往由预测得来，其变动的主要原因是环境的改变和预测的误差，故参数之间的变动相对独立，这也是局部敏感性分析契合实际的原因。

本文所研究问题的目标函数为线性非连续函数，因此不能选用针对连续目标函数的局部敏感性分析方法(如：FAST[24]、DIM[25]等)。而标准回归系数法针对的是无模型的数据，需要建立多元线性回归模型，而本文研究对象就是主动打断项目选择模型，并不需要建立回归模型，故标准系数回归法并不适用。

基于上述两方面的分析，本文将选用局部敏感性分析方法中最为传统且操作简单的敏感性系数法。参数的敏感性系数=∣目标函数值的变动百分比/对应参数的变动百分比∣，其中目标函数值的变动百分比=|ΔW/W|，W代表目标函数值；参数的变动百分比=|Δx/x|，x代表变动的参数。基于敏感性系数法，综合第二节的问题描述，下面将给出适合敏感性分析的动态项目组合选择新模型。在公式(1)和(6)基础上，引入t时间段期初企业通过筹资活动从外部获得的可用于项目执行的资金K(t)，故可得考虑主动打断的项目组合选择模型如下:

(7)

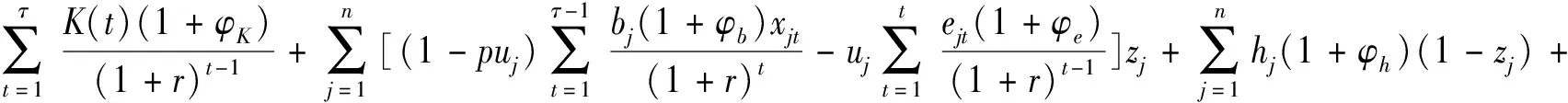
(8)

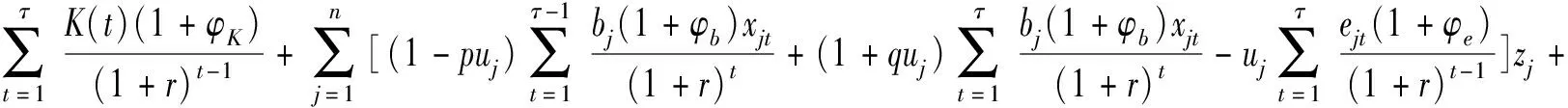
(9)

(10)

(11)

αjtyjt≤xjt≤βjtyjt,yjt∈{0,1},j=n+1,…,|Φ|,t=1,…,|A|

(12)

(13)

xt=(x(n+1)t,x(n+2)t,…,x|Φ|t)T∈R|Φ|-n,t=1,… ,|A|

(14)

yt=(y(n+1)t,y(n+2)t,…,y|Φ|t)T∈{0,1}|Φ|-n,t=1,… ,|A|

(15)

zt=(z1,z2,…,z|Φ|)T∈{0,1}n,t=1,… ,|A|

(16)

uj=(u1,u2,…,un)T∈{0,1}n,j=1,…,n

(17)

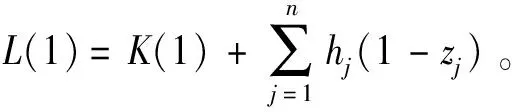
当t=1,…,T时，L(t)可以通过下式获得，即:

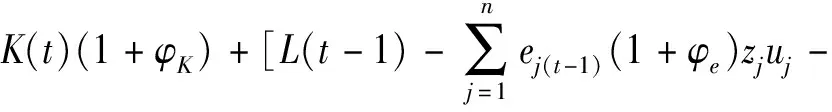
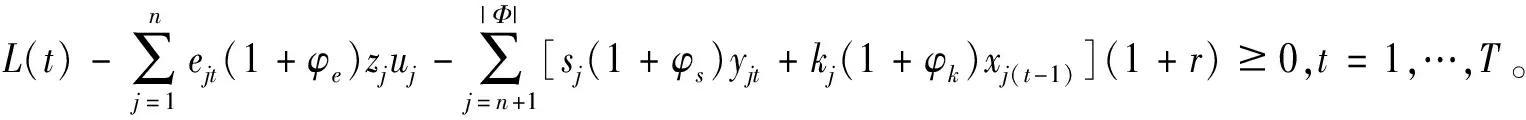
将L(t)带入就可得已有旧项目更新期间的资金约束，即公式(8)。同理，当t=T+1,…,|A|时，可计算求得每个时间段的资金约束为公式(9)。在求解资金约束时，已有旧项目的机会成本并不会引起资金的消耗，故不需要考虑已有旧项目的机会成本。

此外，公式(10)表示第t时间段内执行项目数量的约束；公式(11)表示整个计划投资期内执行项目的数量约束；公式(12)表示项目j在t时间段内执行比例xjt的范围约束；公式(13)表示新项目j的完成约束，即新项目一旦被选择就要在整个计划投资期内全部完成；公式(14)表示执行比例xjt为实数；公式(15)～(17)分别表示yjt、zj、uj为0-1变量。

2.2 动态线性模型

通过引入变量和线性化的方法，根据Glover和Woolsey[26]提供的线性转换方法，2.1中的非线性规划模型可以转化成下面等价的混合0-1整数线性规划模型。

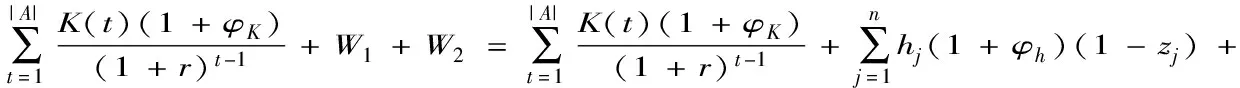
(18)

为了显示动态主动打断项目组合选择线性模型的优越性，下面将给出不考虑已有旧项目的静态主动打断项目组合选择模型(即原模型)，如下所示。

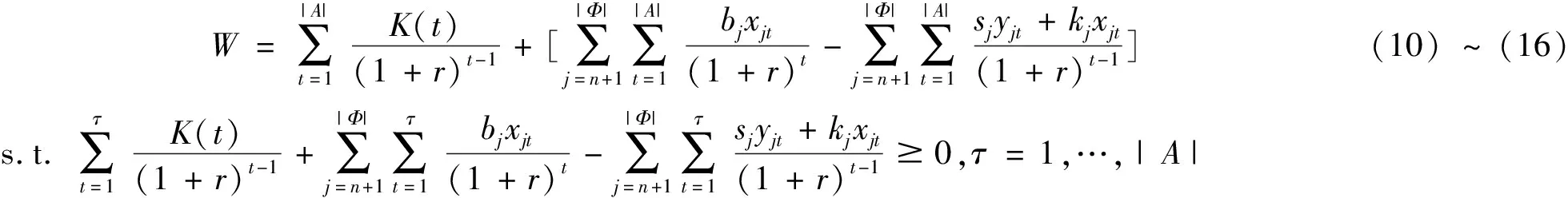
(22)

公式(22)为资金约束，静态主动打断项目组合选择模型不考虑已有项目的更新，资金约束只有一个。该模型为混合整数规划线性模型，包含(|Φ|-n)·(|A|+1)个0-1变量，(|Φ|-n)·|A|个连续变量，|A|(|Φ|+4-n)+|Φ|+1个约束条件。

3 算例及敏感性分析

本部分将以一组仿真数据为例，利用GAMS/BARON求出动态线性模型和静态模型的最优解，分别对动态线性模型中的初始资金K(t)、项目收益bj、新项目的投资kj、新项目的准备成本sj、旧项目的更新费用ejt以及放弃旧项目获得的收益hj这六个不确定性参数进行敏感性分析，并对各参数的敏感程度排序，得出相关结论。

3.1 算例选取

首先假设整个计划期共包括|A|=5个时间段，可供选择的项目总数为|Φ|=10，其中正在执行的旧项目n=5个，备选的新项目5个。假设整个计划期内执行项目的最大数量N=8，每个时间段执行项目的最大数量为M=2，市场利率r=5%，新项目的紧前关系集合为ξ={(6,9),(7,10)}，已有旧项目更新期收益的缩减比例为p=20%，更新期过后收益的增加比例为q=50%。各时间段的初始资金K(t)如表1所示。

表1 各时间段的初始投资

对于已有旧项目j=1,…,5，其在计划期对应时间段的执行比例如表2所示，旧项目收益bj和放弃旧项目获得的收益hj如表3所示，旧项目的更新期T=2，其更新费用如表4所示。

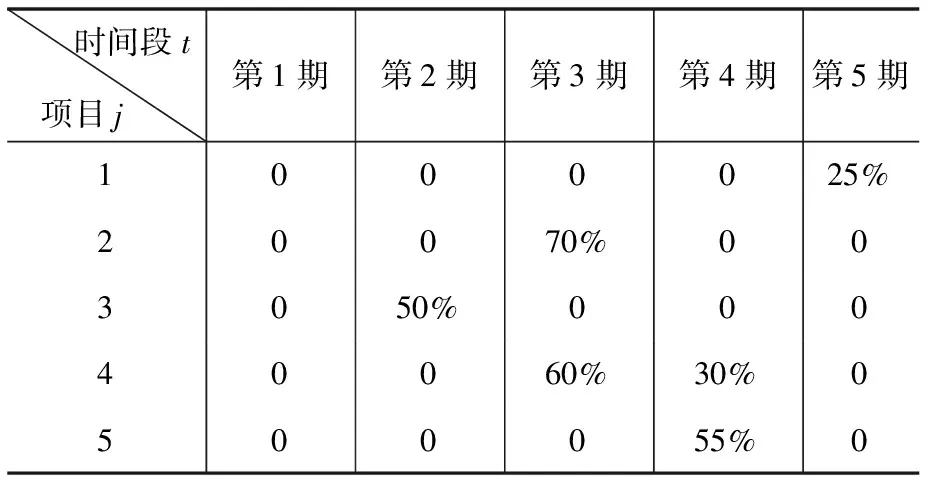
表2 已有旧项目的执行比例

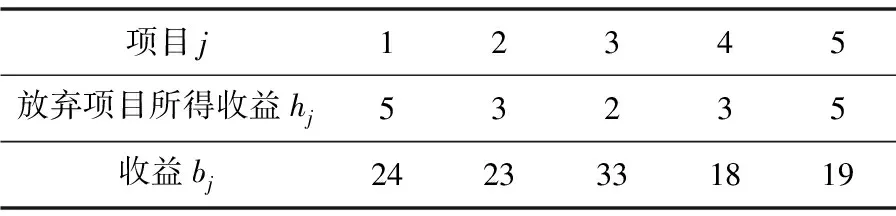
表3 已有旧项目的收益bj和放弃已有旧项目获得的收益hj(百万元)

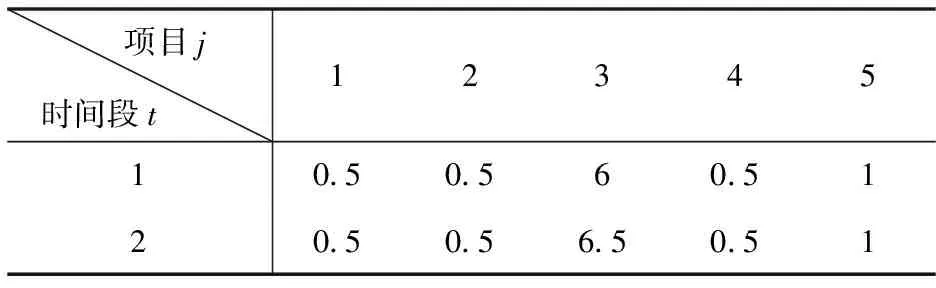
表4 已有旧项目的更新费用ejt(百万元)

对于新的备选项目j=6,…,10，其收益bj、投资kj、准备成本sj以及各阶段最小(大)执行比例αjt(βjt)如表5所示。

表5 新项目的收益bj、投资kj、准备成本sj(百万元)以及各阶段最小(大)执行比例αjt(βjt)

3.2 求解结果

动态主动打断项目组合选择线性模型为混合整数线性规划模型，可用GAMS/BARON进行求解。为了便于对比动态线性模型和静态模型的项目组合选择结果，本部分令六个参数的变动百分比均为0。利用GAMS/BARON求得的动态线性模型的最优解如表6和表7所示。

表6 动态线性模型求得的zj和uj的值(已有旧项目)

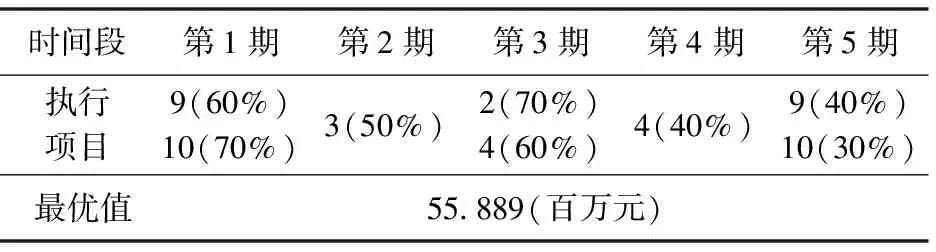
表7 动态线性模型的最优解

对于已有旧项目，zj=0时，表示项目j被放弃并卖掉；zj=1且uj=1时，表示项目j进行了更新；zj=1且uj=0时，表示项目j维持原状。由表6可知，项目1和5被放弃，项目2和项目4进行了更新，而项目3维持原状。

由表7可知各个项目的执行时间段和执行比例，其中9(60%)表示项目9在第1期的执行比例为60%，以此类推。其中项目9、10为新项目，项目2、3和4为旧项目，动态线性模型所得的最优值为55.889百万元。

为了体现动态线性模型的优越性和合理性，下面将用静态主动打断项目组合选择模型来求解问题。使用静态模型时，不考虑企业已有旧项目，默认其维持不变，即zj=1且uj=0。因此5个企业已有旧项目全部入选且维持不变，为了满足整个计划期内选择的最大项目数量N=8，静态模型最多选择3个项目，其最优解如表8所示。

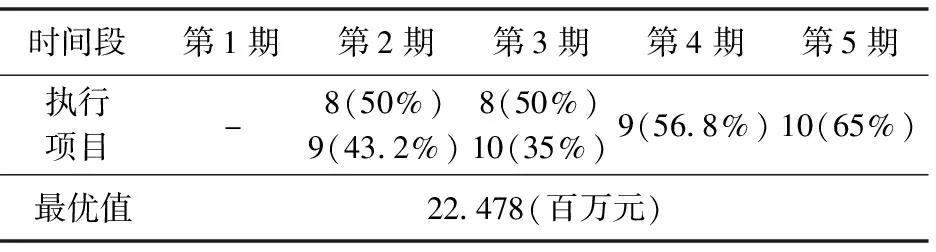
表8 静态模型的最优解

由表8可知，静态模型所得的最优值为22.478百万元。由于静态模型忽略了已有旧项目的执行情况，造成同一时间段内执行的项目数量超过企业的承受范围，如：在第3期已经有旧项目1和3执行，通过静态模型又选出项目8和项目9，这使得该时间段执行的项目数量远远超出了企业的承受范围M=2。

对比可知，较静态模型而言，动态线性模型选出的项目组合的收益得到了较大的提升，而且动态线性模型可以综合考虑新、旧项目的执行情况，统筹安排项目的执行阶段和比例。究其原因，可以归结为以下两方面：其一，动态线性模型在建模的时候，充分考虑了当前市场对企业已有旧项目的需求情况，淘汰掉不具备竞争力的旧项目并获得收益hj，更新具有市场前景的旧项目，动态线性模型在进行项目组合选择时充分挖掘了企业的现有资源，故收益更高；其二，动态线性模型兼顾了企业已有旧项目的执行时间段和比例，选择新项目时进行了充分的考虑，故可以避免单个时间段执行的项目数量超出企业的承受范围。

综上可知，考虑企业已有旧项目的动态主动打断项目组合选择线性模型更符合实际情况，选择新项目的同时，兼顾了当前市场对旧项目的需求情况，所得的项目组合收益更高、更具可靠性。因此，很有必要对动态线性模型做敏感性分析。

3.3 敏感性分析

本部分将针对动态主动打断项目组合选择线性模型进行局部敏感性分析，分别求解初始资金K(t)、项目收益bj、新项目的投资kj、新项目的准备成本sj、旧项目的更新费用ejt以及放弃旧项目获得的收益hj这六个不确定性参数的敏感性系数。分析每个参数变动±5%、±10%以及±20%时，最优值的变动情况。其中一个参数变动，其余参数不变，如：分析初始资金K(t)变动5%时最优值的变动情况时，φK=5%，φb=0，φs=0，φk=0，φh=0，φe=0。

值得强调的是，已有旧项目的初始投资、准备成本被视为沉没资本，在动态线性模型中没有体现，所以不对之做敏感性分析。下面，将分别从最优值和敏感性系数两方面对动态主动打断项目组合选择线性模型进行敏感性分析。

(1)不同参数变动百分比下的最优值

利用GAMS/BARON求得动态线性模型中不确定性参数不同变动比例下的最优值，如表9和图1所示。

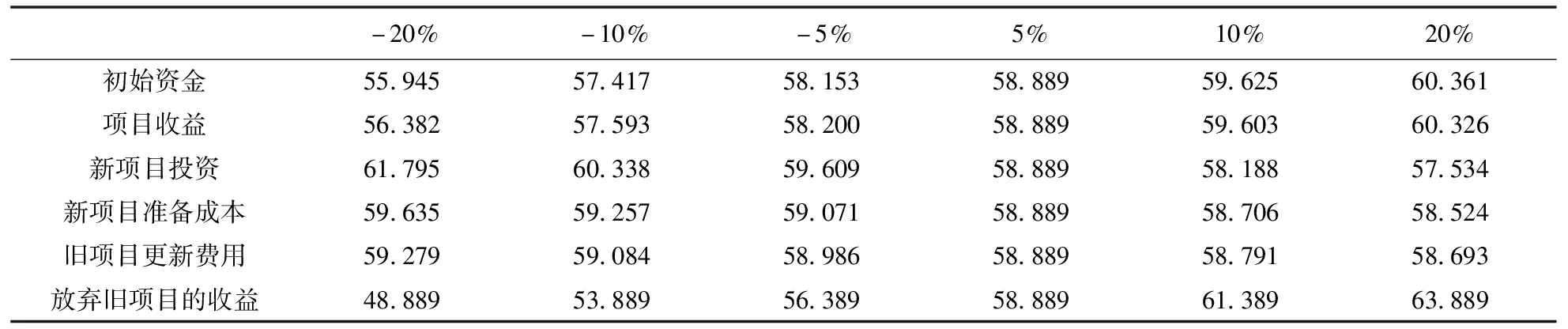
表9 动态线性模型单参数变动情况下最优值(百万元)

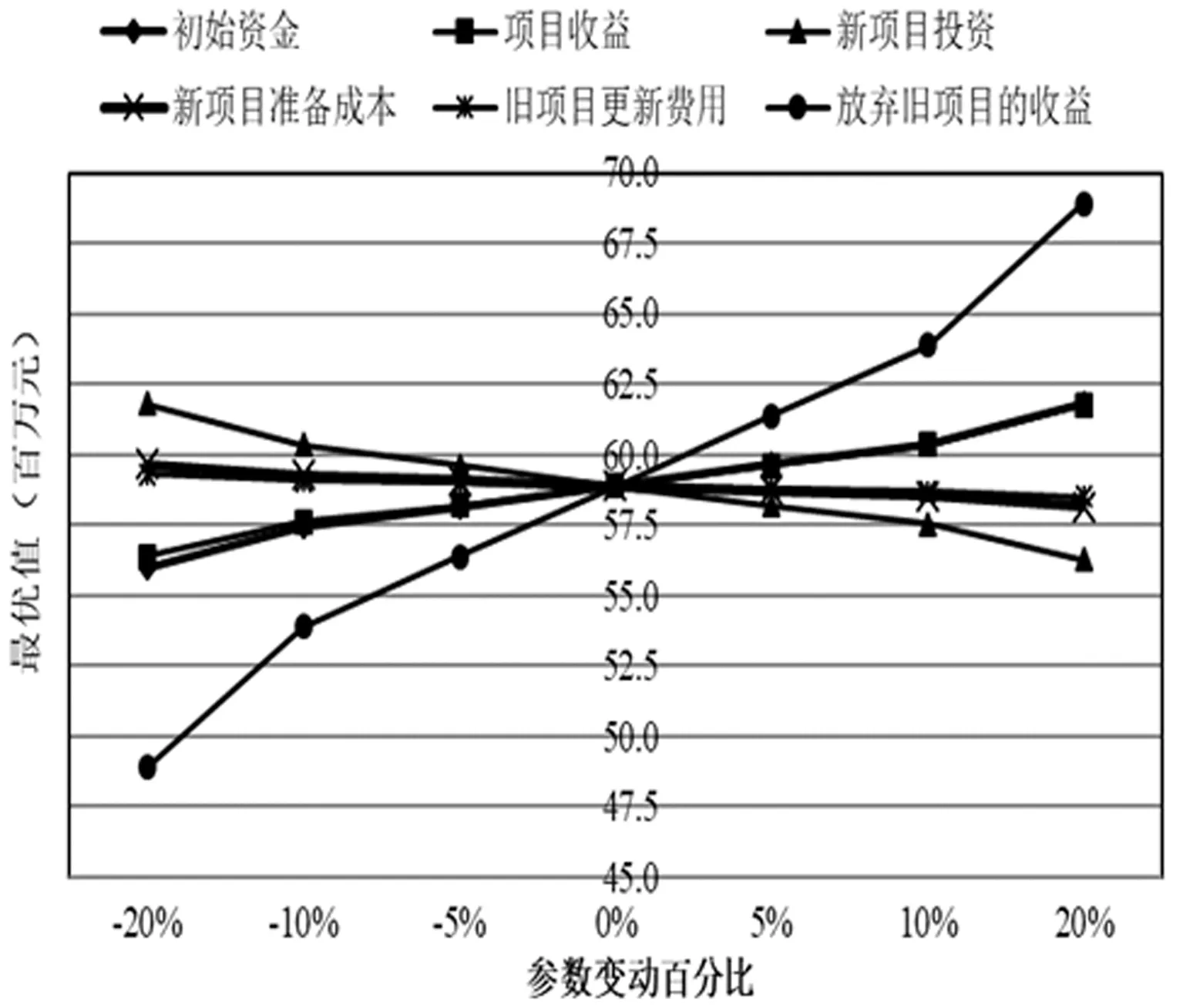
图1 动态线性模型单参数变动情况下的最优值

根据表9和图1可知，对于动态线性模型，参数变动百分比与最优值变动幅度的关系主要体现在三方面。其一，同一个参数变动不同的幅度时，最优值的变动程度也不同，且参数变动幅度越大，最优值变动幅度也越大；不同参数变动相同的幅度时，最优值的变动幅度不相同。其二，最优值会随着成本类参数的增加而减少，随着收益类和融资类参数的增加而增加。其三，项目收益和新项目投资对应的曲线很接近，这意味着这两个不确定性参数的敏感性相似，同理，新项目准备成本和旧项目更新费用的敏感性也相似，后续的敏感性系数变化结果也验证了这一结论。

(2)不同参数变动百分比下的敏感性系数

动态线性模型对应的六个不确定参数的敏感性系数如表10和图2所示。

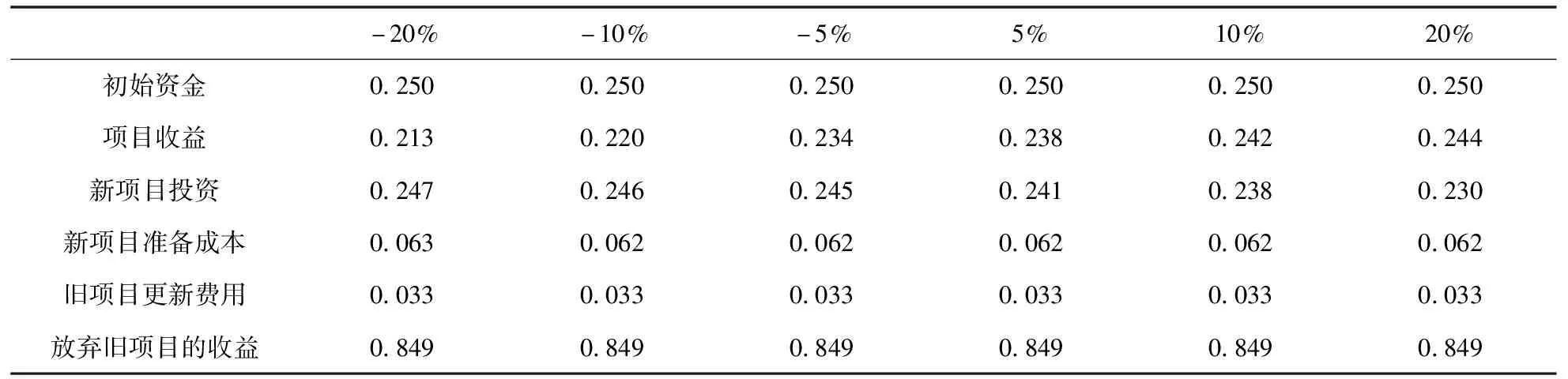
表10 动态线性模型单参数变动情况下的敏感性系数

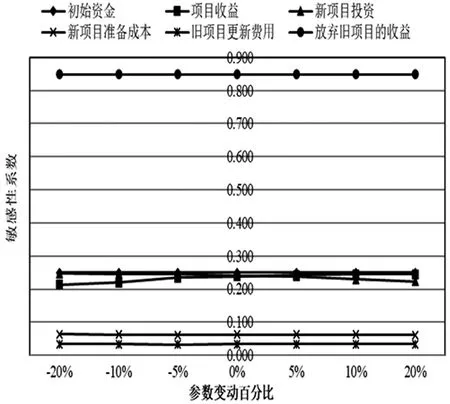
图2 动态线性模型单参数变动情况下的敏感性系数

敏感性系数绝对值越大，其对应的不确定性参数越敏感。按照敏感性系数的大小，根据图2，动态线性模型参数可以分为三组，其敏感性排序为：{放弃旧项目的收益}>{初始资金，项目收益，新项目投资}>{新项目准备成本，旧项目更新费用}。这说明，在本算例中，放弃旧项目所得的收益最为敏感，在项目组合决策中发挥着关键的作用；初始资金、项目收益、新项目投资较为敏感，是影响组合决策的重要因素；而新项目准备成本和旧项目更新费用不敏感，不宜过多关注。因此，在本算例中，如何提高放弃旧项目所得的收益是企业需要考虑的首要问题；其次，企业需要考虑增加融资，提高项目收益，控制新项目的成本；相反的，企业不宜在生产准备成本和旧项目更新费用控制方面投入过多精力。

另一方面，初始资金、新项目准备成本、旧项目更新费用和放弃旧项目所得收益对应的敏感性参数几乎不随着参数的变化而变化。而项目收益对应的敏感性系数随着参数变动的增加而增加，新项目投资的敏感性系数随着参数变动的增加而减小。值得注意的是，参数变动百分比小于零时，新项目的投资敏感性>项目收益的敏感性，参数变动百分比大于零时，项目收益的敏感性>新项目的投资敏感性。这说明，个别参数的敏感性大小和排序会随着参数变动百分比的变化而变化，企业应当格外注意这些参数。具体而言，当参数变动百分比为正且较大时，企业应当着重考虑如何增加项目的收益；当参数变动百分比为负且较小时，企业应当着重考虑如何控制新项目的投资成本。

本文研究的敏感性系数情况较为多样，体现了动态主动打断项目组合选择线性模型中参数敏感性的复杂性，依据本文提供的模型和敏感性分析方法，企业可以对动态主动打断项目组合决策中的不确定参数进行敏感性分析，得出实际项目组合选择时各参数的敏感性排序，集中企业资源尽可能地提高企业收益、降低潜在风险。

综合3.2和3.3的研究内容，针对动态主动打断项目组合选择线性模型，在本文研究的基础上，通过进一步分析大量随机算例，我们可以得出以下结论：

结论1动态主动打断项目组合选择线性模型在选择新项目的同时，兼顾了当前市场对企业已有旧项目的需求情况，可以统筹安排新、旧项目的执行阶段，其收益也更高。

结论2当两个(或多个)不确定性参数对应的最优值曲线很接近时，这两个(或多个)参数的敏感性系数也很接近，其敏感性排名靠近。

结论3新项目投资和项目收益的敏感性大小和排序，会随着参数变动百分比的变化而变化；而其他参数的敏感性，不会随着参数变动百分比的变化发生明显的变化。

4 结论

本文首次对考虑企业已有旧项目的动态主动打断项目组合选择问题进行了局部敏感性分析，构建了适合敏感性分析的动态主动打断项目组合选择新模型，并将之线性化，进而给出利用GAMS/BARON求解的敏感性分析算例，得出了相关结论。本文的贡献主要体现在三方面：1)首次构建了适合敏感性分析的动态主动打断项目组合选择新模型，并对其进行了线性化处理；2)通过GAMS/BARON分别求解新模型在不同参数变动百分比下的最优值，对六个不确定性参数进行了敏感性分析，并得出了敏感性排名和相关结论；3)根据本文的研究结果和不确定性参数的敏感性分析，给出三个对企业有实际帮助的建议，即：①选择新项目时，企业要充分考虑当下市场对企业已有旧项目的需求情况，统筹规划新、旧项目可以使企业获得更高的收益；②企业在应对风险和提升效益时，可以根据不确定性参数的敏感性排序，有区别地对待不同的参数，实现企业资源的有效利用；③企业应当格外注意新项目投资和项目收益这两个不确定性参数，尤其在不确定性参数变动百分比较大的情况下。

本文只对考虑企业已有旧项目的动态主动打断项目组合选择模型进行了局部敏感性分析，实际上项目选择过程中往往伴随着几个参数的同时变化。故研究的下一阶段可探究合适的方法对动态主动打断项目组合选择模型进行全局敏感性分析，尽管全局敏感性问题较为复杂，但其更符合实际，能够全面的反映参数的敏感性以及其对项目组合选择的影响，为企业提供更全面的决策依据。