基于排队系统的偏好差异性顾客服务策略分析
2020-10-24李武强倪冠群许晓晴
李武强, 倪冠群, 许晓晴
(1.长安大学 经济与管理学院,陕西 西安 710064; 2.福建农林大学 管理学院,福建 福州 350002)
0 引言
在诸如咨询、医疗诊断、个人护理等服务中,良好的服务体验往往需要服务员耐心、专注且较长时间的投入,服务效果与服务时间呈正相关关系,具有此类特征的服务也被一些研究者称为顾客密集型服务(Customer-intensive Service)[1~3]。
如何协调服务质量与排队等待是顾客密集型服务研究关注的重点,由于排队模型能够较好的反映服务系统中的排队现象[6,7],因此许多学者结合排队论对此问题进行了研究。Anand等[1]从顾客密集型服务的共性特征出发,基于M/M/1模型研究了同质顾客情景下,服务商如何协调服务质量与效率才能达到系统最优的问题;Debo等[8]针对服务信息不明确且顾客选择具有从众效应的情景进行了研究,指出服务速度的设定应以维持一定的队长为前提;Tong等[9]基于创新导致固定服务时间减少情景,对将“减少的时间”用于提升服务质量还是服务更多顾客的问题进行研究;另外,还有周华等[10]对如何选择服务专家技能水平的研究,Chan等[11]对服务效果较差时会重新服务现象的研究等。然而上述研究并未考虑到顾客的差异性,且仅提供一项服务。
事实上不同顾客对于服务的偏好存在差异,其感受到的效用也不一样[12,13],而服务商在此情景下如何优化服务,实现收益最大化也是需要关注的问题。相关研究方面,Afèche[14]针对偏好和时间敏感程度都存在差异的顾客,研究了如何提供差异性的价格和延迟时间策略的问题;Zhou等[15]基于不同偏好顾客从服务所获效用不同的现象,对于差异性顾客如何统一定价的问题进行了分析;刘健等[16]基于顾客不公平规避偏好心理,分别从社会成本最小化和企业收益最大化角度对是否保留优先权顾客并收取优先服务费用的问题进行了研究;Mccrossan等[17]则从诊断技术偏好角度研究了不同顾客人群对于远程诊断服务的选择问题。但上述研究更关注于服务响应时间,服务方式对于服务系统优化的影响,没有考虑到服务时间的长短对于顾客感受以及服务选择的影响。
顾客往往会根据具体服务情景决定是否选择服务[18],而已有研究也表明为不同的顾客提供针对性的服务策略能够有效提高系统收益[19,20]。现实中,服务商为了节省成本以及满足顾客偏好,往往会在原有服务框架的基础上,对局部内容进行调整形成新的服务,并设定新的价格,期望获得更大的收益,如许多SPA服务仅仅只是耗材方面存在差异。由于主要的成本支出如服务人员、固定投资,以及流程等并未发生明显改变,因此新的服务在服务时间以及成本方面与原来服务并无显著差异。这也就意味着,服务商为差异性顾客提供了具备相同服务时间及成本的多种服务。在此情景下,服务商如何对多种服务共用的服务流程(服务时间)进行调整,价格如何设定才能到达收益最大化?
1 基本假设
本文基于M/M/1排队模型对单一服务商展开分析,顾客一旦选择排队就不能中途退出,服务规则为先到先服务且每次仅能服务一人。为了简化分析,本文假定存在两类不同偏好的顾客,而服务商则根据顾客偏好提供两类服务,定义为服务j,j∈{1,2}。两类服务的服务速度没有明显区别,服从参数为μ的指数分布,价格分别为pi。总的顾客到达速率(潜在到达速率)服从系数为Λ的泊松分布,当顾客到达服务点后将根据服务效用与成本决定是否选择服务,其中选择服务的顾客的到达速率(有效到达速率)为λ;根据偏好的不同可将顾客定义为i类顾客,i∈{1,2},其中1类顾客所占比例为q,2类顾客为(1-q),两类顾客的单位时间等待成本c是相同的。
由于顾客存在服务偏好差异,不同的顾客即使从同一种服务所获得的效用也是不同的[14],本文将服务j对于i类顾客的基准效用定义为vij;基于1类顾客更偏好服务1,2类顾客更偏好服务2的设定且不失一般性,假定min{v11,v22}>max{v12,v21}。定义δ=v22-v11>0,结合现实可以认为服务2相对于服务1是更符合当前需求方向的服务。本文设定为完全信息情景,服务商和顾客对彼此的信息完全了解。另外,由顾客密集型服务中顾客所获效用为服务时间递增凹函数的特点,结合Anand等[1]的研究定义顾客i由服务j所获效用为Uij(μ)=vij-αμ,其中α为顾客关于服务时间的敏感程度。
结合M/M/1排队系统的相关研究可知,当μ<λ时顾客的平均逗留时间W=1/(μ-λ)。由此可得,一定服务速度和价格情景下顾客净效用为Unij(μ,pj)=Uij(μ)-pj-c/(μ-λ)。
假定Unij≥0时,顾客选择服务。结合现实情景可知,当服务商面对两类顾客时,其可选择的基本策略有以下六种:
S1:仅服务1类顾客,排队队列中仅有1类顾客;
S2:仅服务2类顾客,排队队列中仅有2类顾客;
S3:公平策略,同时服务两种顾客,且使两类顾客选择服务的状态相同;
S4:优先服务1类顾客;
S5:优先服务2类顾客;
S6:不服务任何顾客。
以上基本策略中,S1和S2可称为排他性服务策略,因为另一种顾客被排除在服务范围之外;S3为公平服务策略,两类顾客要么同时全部选择服务,要么同时部分选择服务;S4与S5则属于优先服务策略;S6策略下服务商收益为零,不予考虑。
2 排他性服务策略分析
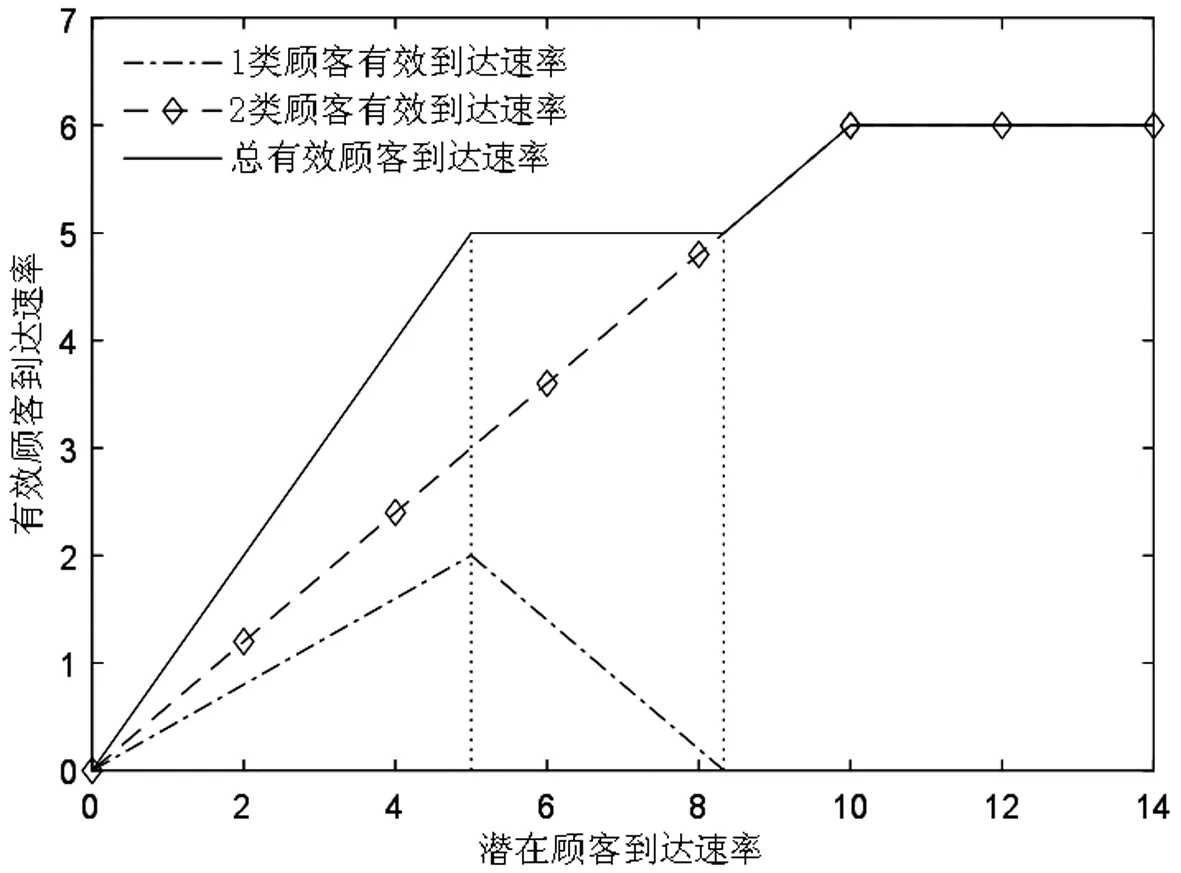
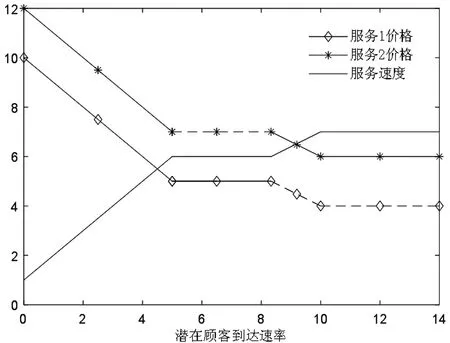
在M/M/1排队系统下,两类顾客的等待时间是相同的。若服务商仅为i类顾客提供服务,那么最直接的方法就是为服务j设定足够高的价格,使得任何顾客选择服务j时净效用都为负,其中i≠j。另外,当仅有服务i可被选择时,服务商的最优策略为设定合适的服务速度μ和价格pi,使得Unii(μ,pi)=0;由假设min{v11,v22}>max{v12,v21}可知,此时若j类顾客选择服务i则其净效用Unji(μ,p) 定义f(i)=q2-i(1-q)i-1,当i=1,2时f(i)分别为q,1-q。 根据顾客对于服务的选择情况,可将Si策略下的情景分为三种:(1)所有i类顾客选择服务,Unii(μ,pi|λ=Λf(i))≥0;(2)无顾客选择服务,Unii(μ,pi|λ=0)<0;(3)仅部分i类顾客选择服务,Unii(μ,pi|λ∈(0,Λf(i))=0。其中,由于情景(2)没有顾客选择服务,所以不予分析。由以上条件可知在策略Si情景下,对于一定服务速度μ、pi,有效到达速率为: (1) 上式中由上至下分别代表了所有i类顾客、部分i类顾客选择服务的情况。由此可将服务商的收益表述为: maxRSi(μ,pi)=piλ(μ,pi) s.t.Unij(μ,pj)<0,i≠j (2) 由于策略Si实质上属于同质顾客选择服务情景,因此可参考Anand等[1]的研究直接得出结论。 在公平策略情景下,服务商会设定合适的服务速度和价格,使得两类顾客选择服务的状态相同,存在以下三种情况:(1)两类顾客全部都选择服务;(2)无顾客选择服务;(3)两类顾客分别仅有部分选择服务。总的有效到达速率λ由1类顾客的有效到达速率λ1以及2类顾客的有效到达速率λ2两部分组成。由于两类顾客各自可选的服务都有两种,情况比较复杂,因此下文首先对顾客选择以及均衡状态下的队列结构进行了分析。 引理1队列均衡状态下,服务商的最优策略必然使得1类顾客选择服务1,2类顾客选择服务2。 证明根据上文所述的3种情景,分别证明引理1。 1)所有顾客都选择服务 当所有顾客都选择服务时,根据顾客对服务的选择可分为:①两类顾客各自同时选择两种服务;②一类顾客同时选择两种服务,另一类顾客仅选择一项服务;③两类顾客分别选择不同服务。此处将采用排除法证明。 ①首先,证明1类顾客和2类顾客不可能同时都选择两种服务。 在均衡状态下,若1类顾客同时选择两种服务,则必然是因为这两类服务对于1类顾客的收益是相同的,否则1类顾客会选择其中收益较高的那个服务,因此可得Un12(μ,p2)=Un11(μ,p1),由此可知: v12-p2=v11-p1⟹p1-p2=v11-v12>0 (3) 同理,若2类顾客同时选择两种服务,则存在Un21(μ,p1)=Un22(μ,p2),由此可知: v21-p1=v22-p2⟹p1-p2=v21-v22<0 (4) 易知式(3)和(4)相互矛盾。因此可得1类顾客和2类顾客不可能同时都选择两种服务。 ②其次,证明一类顾客同时选择两种服务,另一种顾客仅选择一项服务亦非最优情景。此情景的证明分为两种情况,如下所示。 第一,证明i类顾客同时选择两种服务,而j类顾客仅选择服务i非最优情景,i≠j。与证明①类似,此处省略。 第二,证明i类顾客同时选择两种服务,而j类顾客仅选择服务j非最优情景,i≠j。 同理可得,2类顾客同时选择两种服务,而1类顾客仅选择服务1非最优情景。 综上可知,情景②非最优情景。 ③最后,证明i类顾客选择服务i的情景要优于i类顾客仅选择服务j的情景,i≠j。 若i类顾客选择服务j而非服务i,则表明其选择服务j的净效用更高,即Unij(μ,pj)≥Unii(μ,pi),由此可以得出: Un12(μ,p2)≥Un11(μ,p1)⟹p1-p2≥v11-v12>0 (5) Un21(μ,p1)≥Un22(μ,p2)⟹p1-p2≤v21-v22<0 (6) 综上所述,由证明①、②及③可知,当所有顾客都选择服务时,在服务商的最优策略下,1类顾客选择服务1,2类顾客选择服务2。 2)无顾客选择服务 无需证明。 3)部分顾客选择服务 在公平策略中,若部分顾客选择服务,则所有顾客的净效用均为零;否则,未选择服务的顾客会加入排队队列,使得等待成本上升。这些顾客的加入会导致两种结果,要么即使所有顾客都加入,其净效用依然大于零,此时转变为情景1)所有顾客选择服务;要么等待时间的变长使得顾客所得收益为零,不再有新顾客加入。因此,当部分顾客选择服务时,必然是所有顾客净效用为零。根据顾客对服务的选择,将其表示为: Un11(μ,p1)=U11(μ)-p1-c/(μ-λ)=0 (7) Un12(μ,p2)=U12(μ)-p2-c/(μ-λ)=0 (8) Un22(μ,p2)=Un22(μ)-p2-c/(μ-λ)=0 (9) Un21(μ,p1)=U21(μ)-p1-c/(μ-λ)=0 (10) 由于min{v11,v22}>max{v12,v21},因此(7)和(10)、(8)和(9)不可能同时存在。这就意味着,顾客对服务选择的情景只有两种,即a.1类顾客选择服务1,2类顾客选择服务2;b.1类顾客选择服务2,2类顾客选择服务1。显然,情景a要优于情景b。 通过上述三种情景的证明,可知在服务商的最优策略下,1类顾客选择服务1,2类顾客选择服务2。 引理2-1队列均衡状态下,当服务所有顾客时,服务商的最优策略为使得所有顾客净效用为零。 若存在i类顾客的净效用大于零,此时若保持服务速度不变,仅在保证所有顾客选择服务的前提下适当提高服务价格使得此类顾客净效用为零,即可使服务商获得更高收益。由此可知,当所有顾客都加入排队队列时,服务商最优策略是采用合适的价格使得顾客净效用为零。而仅有部分顾客选择服务时,则其净效用必然为零。 引理2-2队列均衡状态下,当仅服务部分1类顾客和2类顾客时,顾客净效用为零。 引理3在最优的公平策略S3情景下,λ1/λ2=q/(1-q)。 证明首先,当服务商采用公平策略服务全部顾客时,顾客有效到达速率即为潜在到达速率,因此λ1/λ2=q/(1-q)。 其次,当服务商采用公平策略服务部分顾客时,由引理2-1和2-2可知,服务商为了获得最大收益必然会制定相应的策略,使得i类顾客仅选服务i,且队列均衡状态下所有顾客的净效用Unii(μ,pi)=0。另外可知: 1类顾客选择服务的决策依据为:Un11(μ,p1)=v11-αμ-p1-c/(μ-λ)≥0; 2类顾客选择服务的决策依据为:Un22(μ,p1)=v22-αμ-p2-c/(μ-λ)≥0。 定义z为顾客从服务所获效用与支付价格之差,由Unii(μ,pi)=0可知z=v11-αμ-p1=v22-αμ-p2,因此可以将1类、2类顾客选择服务的决策依据改写为Un=(μ)=z-c/(μ-λ)≥0,这表明最优的公平策略下顾客是否选择服务与顾客类型无关。由M/M/1模型队列均衡状态的特征可知,在充分小的时间段[t,t+Δt)到达1个有效顾客的概率为λΔt,此顾客的类型仅依赖于潜在顾客的结构,即其为1类顾客的概率为q,2类顾客的概率为(1-q),因此可知在[t,t+Δt)到达1个1类顾客的概率为qλΔt,2类顾客的概率为(1-q)λΔt,所以队列均衡状态下1类顾客与2类顾客的有效到达速率之比为q(1-q)。 综上可知,在最优的公平策略S3情景下λ1/λ2=q/(1-q)。 由引理3可知一定价格pj以及服务速度μ情况下,1类顾客的有效到达速率λ1=qλ(μ,pj),2类顾客的有效到达速率λ2=(1-q)λ(μ,pj),因此服务商的收益函数可表述为R(μ,pj)=[p1q+p2(1-q)]λ(μ,pj)。 同时,由引理2-1和2-2可知,服务商为了获得最大收益会设定相应的策略使两类顾客的净效用均为零,即Un11(μ,p1)=Un22(μ,p2)=0,由此可得p2=p1+δ,将其代入R(μ,pj)后服务商的收益函数转变为基于1类顾客的函数。综上可得,策略S3情况下服务商的目标函数为: maxR(μ,p1)=[p1+(1-q)δ]λ(μ,p1) (11) 由上式可得最优公平策略。 策略S4为优先服务1类顾客,结合上文最优策略的规律以及顾客的服务选择,可将服务状况分为三个阶段:1)当潜在到达速率较少时,服务所有顾客;2)当潜在到达速率大于某个临界值时,服务所有1类顾客以及部分2类顾客;3)当潜在到达速率足够大时,仅服务1类顾客。其中,阶段1)与策略S3中服务所有顾客情景是相同的;阶段3)则与策略S1相同。因此,仅有阶段2)属于策略S4的独有情景,所以本部分进一步将策略S4定义为“服务所有1类顾客以及部分2类顾客”的策略,并对其进行讨论。 若要保证所有1类顾客以及部分2类顾客选择服务,则需保证λ>qΛ,即总的有效到达速率大于1类顾客的潜在到达速率,且: Un11(μ,p1)=U11(μ)-p1-c/(μ-λ)>0 (12) Un22(μ,p2)=U22(μ)-p2-c/(μ-λ)=0 (13) 其中,(12)式表明1类顾客选择服务1的净效用大于零,由此可确保所有1类顾客都会选择服务;而(13)式则是仅部分2类顾客选择服务的必要条件。 易知,在所有1类顾客都选择服务的前提下,提高服务1的价格,使得Un11(μ,p1)→0+时,不会影响1类顾客的服务选择且能使服务商获得更大收益。因此,可取极限值令服务1价格p1=U11(μ)-c/(μ-λ)。而顾客有效到达速率λ(μ,p2)则由式(13)确定,此时可得服务商的收益: maxR(μ,p2)=max{p1qΛ+p2(λ(μ,p2)-qΛ)} =max{p2λ(μ,p2)}-qδΛ (14) 式(14)中前半部分是仅服务部分2类顾客时服务商的收益最大化问题,而后半部分则与决策变量无关。 同策略S4分析类似,可进一步将策略S5定义为“服务所有2类顾客以及部分1类顾客”的策略。同样,若要保证服务所有2类顾客以及部分1类顾客,则需保证λ>(1-q)Λ,且Un11(μ,p1)=0,Un22(μ,p2)>0。令p2为Un22(μ,p2)→0+的极限值,可得服务商的目标收益函数maxR(μ,p1)=max{p1λ(μ,p1)}+(1-q)δΛ。与策略S4分析类似,此处直接给出结论。 (15) 通过以上三部分的分析比较,可给出服务商在不同潜在到达速率情景下的最优策略,如下所示。 定理7服务商的最优选择为 由定理7可知,随着潜在到达速率的增加,有效顾客中1类顾客所占比例越来越少。另外,三种基本策略关于潜在到达速率的适用范围仅与1类顾客特征相关,这主要是因为服务商从1类顾客所获得的收益相对较少,策略变更的主要目的在于调整有效顾客中1类顾客的比例,从而保障更多的2类顾客选择服务。这也在一定程度上说明当顾客足够多时,服务商更愿意提供符合当前需求倾向的服务,而服务1相对来说仅仅是潜在顾客较少时避免服务资源浪费的手段。 假定某服务商提供两种服务,服务1对于1类顾客的基准效用v11=12,服务2对于2类顾客的基准效用v22=14,两类顾客对服务的敏感系数均为α=1,单位时间等待成本c=1,潜在顾客中1类顾客所占比例q=0.4。 图1 各基本策略的收益 图2 最优策略下各类顾客的有效到达速率 图3显示了在最优策略下服务价格及速度的变化情况,其中当Λ∈(5,8.33)时p2应略低于虚线所示价格,以保证所有2类顾客选择服务;当Λ≥8.33时p1应大于虚线所示价格,以便将1类顾客排除在服务范围之外。整体上来看,服务速度是关于潜在到达速率的非减函数,而服务价格则相反,这种情况也反映了顾客密集型服务的特点,即随着服务时间的减少,顾客愿意支付的价格也随之降低。另外,价格p1与p2线段在不同阶段呈平行关系,且二者之差与基准效用v11、v22的差相关。 图3 最优策略下的服务价格与速度变化情况 现实中,顾客对服务的偏好是不同的,而服务商为了满足顾客的偏好,往往会在原有服务框架的基础上,对局部内容进行调整形成新的服务。另外,在很多情景下这些服务都可以由同一个服务人员或者团队提供,并且服务时间和过程往往没有显著差别。本文针对上述情景进行研究,结果发现:①采用区别定价的策略能够使得服务商获得最大收益,且价格设置的基准为使得顾客从偏好服务中所获净效用尽可能的小;②有效到达速率中1类顾客所占比例(λ1/λ)是关于潜在到达速率的非増函数,其主要原因在于服务商能够从每位2类顾客获得更高的收益,当潜在顾客增加时可以通过服务定价将1类顾客排除在服务范围之外,从而达到服务更多2类顾客的目的;③服务速度是关于潜在顾客到达速率的非减函数,而价格则相反,这一现象由顾客密集型服务的特点决定,即顾客愿意为较长时间的服务支付较高的价格。 另外,从服务效率来看,随着顾客群体的增加,最优策略存在两个“瓶颈期”,即单位时间内完成服务的顾客数量保持不变。其一为优先服务策略阶段,其二为排他性策略阶段且顾客群体大于一定临界值时。出现此现象的主要原因是在此阶段服务商需要维持一定的等待时间,以保证有相应的顾客参与服务。而服务商收益在第一个瓶颈期保持增长,在第二个瓶颈期达到最大。



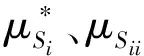
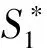
3 公平服务策略S3分析
3.1 服务选择及队列结构分析
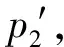

3.2 模型构建及策略分析

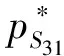
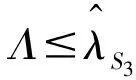
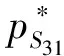
4 优先服务策略分析
4.1 策略S4分析

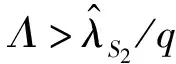
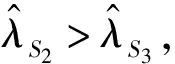
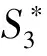
4.2 策略S5分析


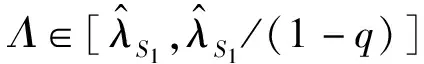
5 最优策略分析
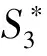
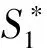

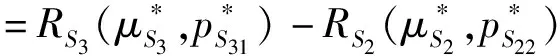
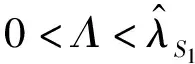

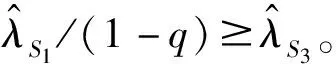
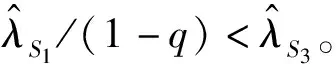
6 算例分析

7 结论
