短期股票价格预测的时序权重均值模型构建

赵庆国，孔祥月，刘莉明，杨龙倩

(沈阳航空航天大学 经济与管理学院，沈阳 110136)

随着我国经济高速发展，国民积累了越来越多的闲置资金。金融市场中最主要的金融工具之一股票成为国人重要的投资渠道被广泛普及。在近年来全球经济普遍低迷的环境下，实体经济萎靡不振，投资渠道缩窄，出于保值增值的目的大量资金涌入股市，股价能否预测以及如何预测,是广大投资者所关注的热点。

2013年，Eugene Fama等借由“可预期性”研究获得诺贝尔经济学奖，他们认为股票和债券的短期价格预测是不可行的，但是却在长期预测上具有可行性。在成功证实了股票长期预测可行性的假设后，短期内股价是否可以预测、怎样预测进一步成为学者们研究的热点。

大部分股民在股价预测时采用简便可行的算术平均数法估计股价，但我们通过对金融市场的观察可以发现，历史股价随着时间由远及近对未来股价期望值的影响是不一样的。比如说，一个之前股价表现很差而最近表现很好的证券要比之前表现很好而最近表现很差的证券具有更高的期望，即对不同时期的证券收益率关注度具有差异，我国学者王振山[1]和林虎[2]曾就关注度与证券收益率之间的关系做过研究，结果表明关注度与股票收益率之间存在联系。而股民们普遍采用的算数平均数法将每期历史股价等量齐观，赋予相同权重值，缺乏对新信息的重视。因此本文参照会计学中固定资产折旧采用的年数总和法，基于厚今薄古思想对历史股价由远及近赋予递增的权重，提出一种短期股价预测模型即时序权重均值模型。

1 文献回顾与分析

国内外学者探究了诸多股价预测模型。早在2009年，依据建模理论，沈巍[3]已将国内外股票价格预测模型划分为两大类:以统计原理为基础的传统型波动率预测模型(ARCH模型和SV模型)和创新型预测模型(神经网络、灰色理论、支持向量机等)。我国学者郑亚磊[4]将股市预测基本方法分为基本面分析方法、技术分析方法、时间序列分析法和人工神经网络预测法。近年主要以时间序列预测模型、神经网络模型和支持向量机模型为主。

时间序列模型主要通过统计软件对历史股价有利信息的提取构建预测模型。覃思乾[5]建立基于小样本的GM(1,1)模型，选取波导股份股价数据检验模型精度并与ARIMA模型对比分析，结果表明短期预测中GM(1,1)模型预测效果优于ARIMA模型。吴玉霞[6]建立基于大样本的ARIMA模型，并选取“华泰证券”250期历史收盘价从动态和静态两个角度对未来三期股价进行预测，结果显示模型拟合效果良好。张斌[7]针对不同波动程度的股价建立了基于ESN的行业通用模型和KMeans-ESN预测模型，通过仿真实验发现股价短期预测中当数据波动较大时适合采用基于ESN的行业通用模型，反之采用KMeans-ESN预测模型。

神经网络模型和支持向量机模型(SVM)均是非线性的系统预测模型。White[8]首次将BP神经网络模型应用于预测股价中，但由于算法存在缺陷导致预测准确度较低。随后一些学者结合不同智能算法通过优化权值和阈值缩小神经网络模型对股价的预测误差。李松[9]采用粒子群算法、孙晨[10]等使用布谷鸟算法、郭建峰[11]采用LM和GA算法等优化神经网络。随着数据挖掘和人工智能的进一步发展，支持向量预测模型(SVM)出现。彭丽芳[12]构建了基于时间序列的支持向量机模型(SVM)，以沙河股份为样本选取84天交易日收盘价数据为基期预测第85日收盘价，预测结果优于神经网络模型和时间序列模型。Francis[13]采用支持向量机模型(SVM)预测期货数据，相较于神经网络模型支持向量机模型(SVM)具有更高的泛化能力和预测精度。

为克服单一模型预测准确度不高的问题，混合模型备受追捧。肖祎平[14]将几种表现较好的预测模型(ARIMA、GM(1.1)等)进行组合，对每个模型的预测结果赋予不同权重组合成新的预测值，研究结果表明组合模型的预测效果高于单一模型。Guresena[15]组合GARCH 模型和ANN 模型对股价进行预测。陈亚静[16]等结合非线性自回归模型(NCF)与粒子滤波(PF)，选取邯郸钢铁股票的171期历史收盘价进行股价实时预测，发现组合后的PF-NCF预测模型的预测准确度高于传统的NCF模型。

现有股价预测模型构建比较复杂，需要借助统计软件回归或训练机器学习，不适合广大投资者的实际应用，而普遍采用的算数平均法缺乏对时间序列的考虑，导致预测准确度较低。所以本文提出的时序权重均值模型具有较好的现实意义和实用价值，时序权重均值模型是基于厚今薄古的思想，考虑时间序列，对历史股价由远及近赋予递增权重的一种股价预测模型。它具有计算简便和预测精度良好的优势，在广大股民预测股价时具有较好的适用性。

2 时序权重均值模型构建

2.1 构建原理

时序权重均值模型的提出源于会计学中固定资产折旧的年数总和法思想。年数总和法认为固定资产贬值速度是经历一个先快后慢的过程的，所以在对固定资产计提折旧时，随时间增长对固定资产计提折旧的权重值呈递减趋势。每期计提折旧的权重值的设定不同，假如该固定资产可使用年限为m年，那么第一年的折旧权重值为m/(1+2+…+m)，第二年权重值为(m-1)/(1+2+…+m)，…，第m年折旧权重值为1/(1+2+…+m)。即分母为该固定资产可使用年限的加总，分子为截至该期的尚可使用年限，折旧权重值的加总为1。

然而，相对于年数总和法计提折旧中的厚古薄今思想来说，对股价的预测与之相反，采用厚今薄古、新信息优先的思想。由于证券市场不稳定，在一定程度上投资者对证券投资相关信息的掌握会受时间变化及外部环境影响，离预测期越近的历史价格对预测期的参考价值越大，离预测期较远的历史价格对预测期的参考价值相对会小一些。因此，随着与预测日距离由远及近的变化，我们对历史股价赋予递增的权重值，依据时间远近量化个股历史价格的时序信息，借以度量不同时期历史股价对预测值的影响。

2.2 模型设计

(1)权重设置

……；

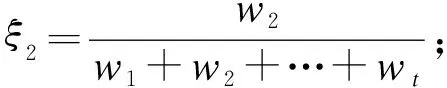
(2)时序权重均值模型构建

(1)

为计算简便适用广泛，同时使预测值能够更好地反映股价走势，本文将股票历史收盘价权重由远及近赋为等差数值且递增，具体权重赋值以样本涵盖的时序区间的加总∑t为分母，样本时序t为分子，对相应时序的股票历史收盘价进行权重赋值，即设w1=1；w2=2,…,wt=t，每期的权重值ξi=i/(1+2+…+t)，其中i∈(1，t)。预测值中更加强调股价之中包含的新信息，进而求得时序权重均值模型的预测值，具体赋值情况如式(2)所示。

(2)

(3)时序权重均值模型与算数平均数法的区别

例如，下面是连续三期的某两只股票收盘价的时间序列数据。

表1 某两支股票连续三期收盘价数据

采用算术平均法和时序权重均值模型分别计算，得出如下结果：

通过上述计算可以看到时序权重均值模型的计算与算术平均法计算的均值的区别。时序权重均值模型更加重视股票近期的收盘价包含的信息，预测值对股价的变化反应灵活，更好反应股价未来发展趋势。

3 时序权重均值模型预测精度对比研究

3.1 数据来源和样本筛选

本文随机选取中国A股市场中的207支股票作为研究样本，其中已经剔除ST、*ST类和数据缺失的股票。为更好检验预测效果，本文选取2018年1月1日至2018年12月31日共243个交易日的收盘价作为预测数据，所有数据均来源于CSMAR数据库。本文所有运算采用JAVA和EXCEL 2010软件。

3.2 预测区间选取

对于短期预测的时间段选取，考虑到股票市场时常处于调整状态[7]，同时借鉴周兆麟和吴玉霞等学者的经验，主要选用了不超过五天的历史收盘价为预测基期数据。鉴于动态预测容易产生累积误差[6]，本文主要是静态预测，即用可获得的历史股价预测接下来的走势。同时西方股市常常选取好几种项数(时间段)对比分析其走势预测的准确性，本文也选取了三种不同区间预测。一是基于连续三日(T=3)历史收盘价预测接下来第四日收盘价，即1月2日-4日作为基期预测5日，1月3日-5日作为基期预测8日……12月25日-27日作为基期预测28日，共计观测240次。二是基于连续四日(T=4)历史收盘价预测接下来第五日收盘价，即1月2日-5日作为基期预测8日，1月3日-8日作为基期预测9日……12月24日-27日作为基期预测28日，共计观测239次。三是基于连续五日(T=5)历史收盘价预测接下来第六日收盘价，即1月2日-8日作为基期预测9日，1月3日-9日作为基期预测10日……12月21日-27日作为基期预测28日，共计观测238次。具体样本区间如表2所示。

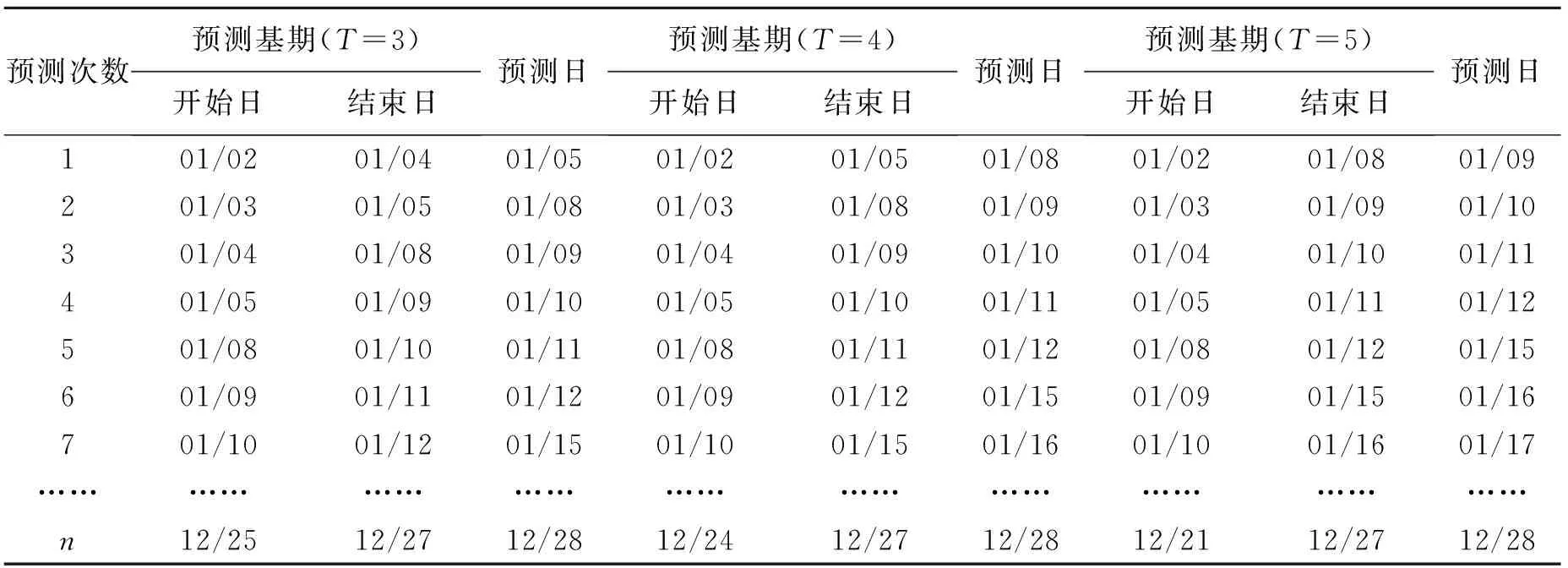
表2 预测区间

3.3 模型建立

基于T=3/4/5三个预测区间下，两种方法的计算如下。

(1)算数平均数法预测值的计算,见式(2)-(4)所示。

(2)

(3)

(4)

其中：p1、p2、p3、p4、p5是按时间升序排序的连续五天历史收盘。

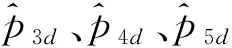
(2)时序权重均值模型预测值的计算,见式(5)-(7)所示。

(5)

(6)

(7)

其中：p1、p2、p3、p4、p5是按时间升序排序的连续五天历史收盘价。

3.4 模型预测精度检验方法

图1 两种方法股价预测值与实际值组合图

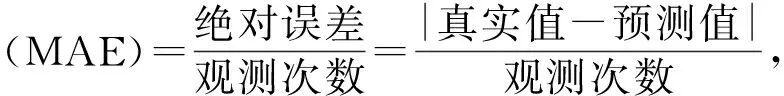
4 时序权重均值模型预测结果与分析

4.1 时序权重均值模型和算数平均数法预测精度结果对比

根据式(2)-式(7)计算两种模型在三个基期下的预测值，为使预测精度具有对比性，又进一步计算了平均绝对误差(表3)，同时为使结果更直观，将两种方法按预测时间绘制成预测年线。主要反应一年之中(本文的样本年为2018年)股价真实值走势、算数平均数预测值走势和时序权重均值模型预测值走势，判断哪一种预测方式下的预测值与真实值走势趋同(图2)。同时，为清晰看到两种方法的误差情况，绘制了误差差值图(图3)，由于受篇幅限制，本文仅列出五天预测区间下的情况。

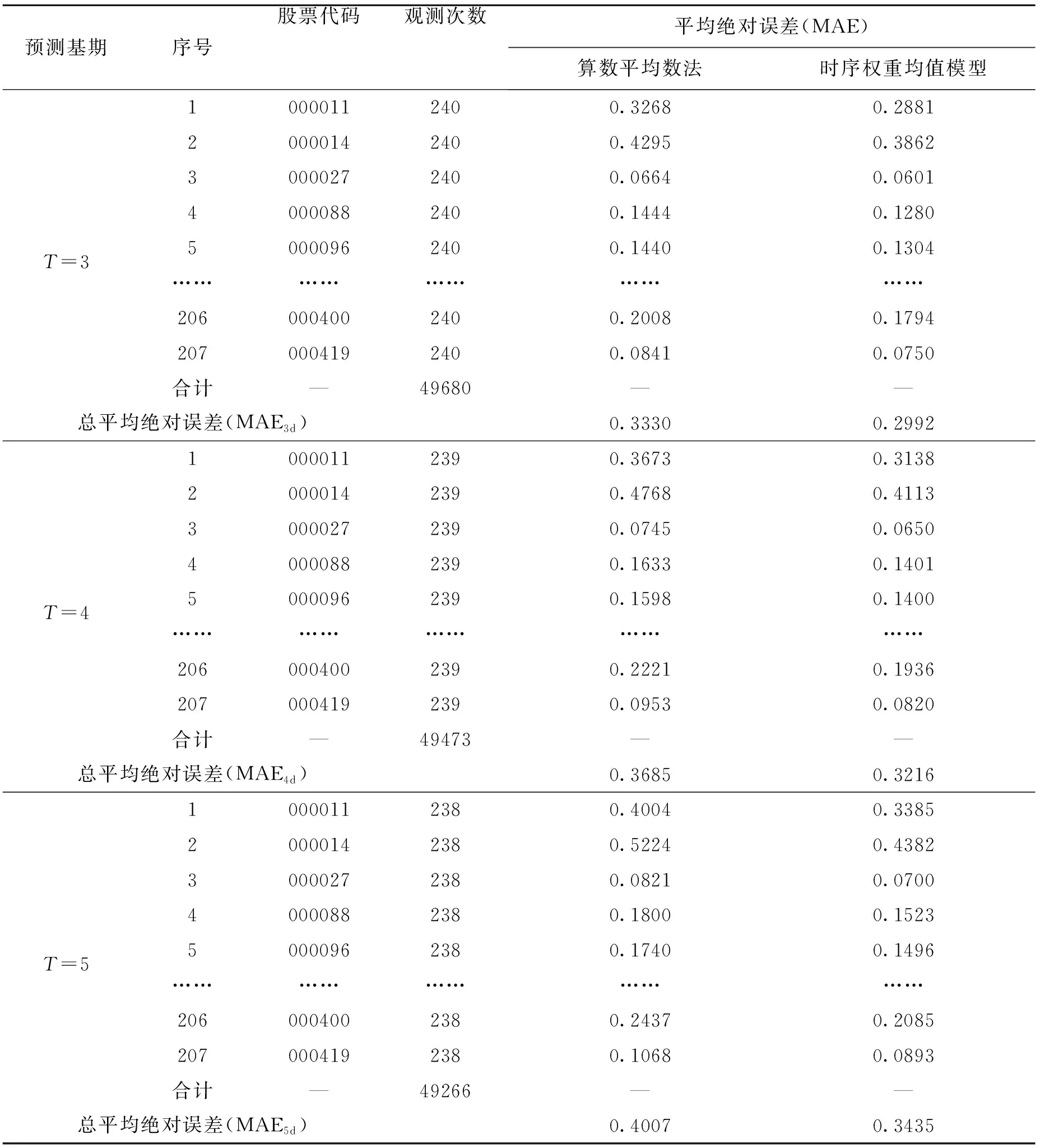
表3 预测精度表

图2 T=5时两种方法预测精度图

图3 T=5时两种方法平均绝对误差图

4.2 预测效果分析

(1)207支样本股票分别采用了时序权重均值模型和算数平均法两种方法预测，每只股票观测次数最高达240次，预测精度表(表3)中的平均绝对误差(MAE)显示，从基于三日、四日和五日预测的整体效果上来看，时序权重均值模型预测值的平均绝对误差(MAE)均低于算数平均数法，表明该种方法精准度更高。观察图2可以看出，当股价发生变化时，算数平均数法的预测值存在更长的滞后性，相较之下时序权重均值模型对股价变化的反应更加灵敏。比如当真实股价呈上涨趋势时，时序权重均值模型的预测值也更倾向于上涨，更好地反应实际情况，而算数平均数上涨幅度则较低，反应速度较慢。图3显示时序权重均值模型的平均绝对误差(MAE)更接近0，误差值显著小于算数平均数法。因此，时序权重均值模型具有较好的预测效果。

(2)进一步发现不同预测基期所产生的预测效果也具有差异，一是随着预测基期的增长，时序权重均值模型预测值的平均绝对误差(MAE)逐渐增长，二是随预测基期的增长，两种方法平均绝对误差(MAE)之差呈上升态势。基于三、四、五日基期下预测股价，时序权重均值模型预测的平均绝对误差(MAE)相较于算数平均数法分别降低了0.1015、0.1273、0.1428。综合来看以连续三日历史收盘价为预测基期，预测日为第四日时，时序权重均值模型的预测效果优于以四天和五天为基期的预测效果。

5 结论

本文在传统的预测手段之外，基于厚今薄古、新信息优先理论，吸取会计学中固定资产折旧的年数总和法思想，对历史股价注入时间概念，提出一种短期股价预测模型即时序权重均值模型。时序权重均值模型利用简单的时间序列对不同时期收盘价赋予不同的权重计算预期收盘价，是一种简便高效的方法，克服了常用的算数平均数法的滞后性，对股价的变化具有更强的敏感性和灵活性，能更好地反映证券价格的走势，具有较好的实际应用价值。

证券投资时短期股价的变化趋势是投资者关注的重点，准确预测股价变化可以帮助投资者规避风险。本文构建的时序权重均值模型相较于投资者普遍采用的算数平均数法，在股价预测中具有更好的适用性，能平均降低11.6%的误差，提高了投资者股价预测精确度，进一步提高了规避市场风险的能力。

时序权重均值模型的清晰明了、简便易算及预测精准度高等优势，具有较好的运用空间和前景。时序权重均值模型在实际应用中可以有更广泛的探究，如探究该模型的泛化能力。本文研究的是基于连续三天、四天和五天历史收盘价预测接下来一天收盘价，未来可深入探讨预测日分别为周一至周五时预测效果是否有差异等。且本文仅预测一期股价，未来可探究多期的动态预测效果。