有源压制干扰下的相控阵雷达多目标跟踪时间资源优化配置算法

陶庭宝，张 弓，张劲东

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

相控阵雷达（Phased array radar, PAR)使用电子转向阵列天线，拥有极端的波束灵活性，可以根据任务需要快速调整波束指向和驻留时间，这种特性使得PAR 能够快速、自适应地定位目标和调整各目标的照射时间[1]，因此非常适用于针对不同应用背景的多目标跟踪任务，例如空中交通管制和反导弹防御等。然而雷达资源有限，如何合理、有效地分配这些资源成为能否充分发挥PAR 优越性的关键。

目前，针对PAR 多目标跟踪资源优化问题已经有许多优秀的研究成果。文献[2]提出了基于灰色关联度的自适应多目标跟踪时间资源调度算法,该方法以灰色关联度为度量函数建立资源管理模型；文献[3]针对波束和驻留时间联合优化问题，提出了一种先确立波束指向再分配驻留时间的两步优化算法；韩清华等考虑了环境和目标特性的不确定性因素，提出了一种基于机会约束规划的阵列雷达功率资源管理算法[4]，并在此基础上提出基于机会约束规划的能量和波束资源联合优化算法[5]；Peter 等提出一种基于雷达组网的资源优化方法[1]，多部PAR 通过通信链路进行数据交换，实现了雷达组网的资源最优调度；此外，严峻坤等从单部雷达跟踪多目标和多部雷达跟踪多目标等多个角度对雷达波束、时间和功率等资源优化问题进行了系统的研究[6-9]。

复杂电磁环境下的电子对抗(Electronic counter measurement，ECM)使得雷达生存环境越发恶劣，同时给雷达资源优化配置带来新的巨大挑战。电磁干扰方式主要分为压制干扰和欺骗干扰[10],其中有源压制干扰是目前最为常见的干扰方式，由远距离支援干扰机或目标自携干扰机向雷达发射干扰信号，掩盖目标回波，致使雷达无法有效探测。然而针对干扰条件下的雷达资源优化问题的研究并不多，文献[11]从任务调配的角度给出了相控阵雷达应对多假目标欺骗干扰的有效策略；文献[12]针对远距离支援干扰和距离门拖引干扰同时存在的情况，从目标探测角度提出了一种能量优化算法；文献[13-14]则从相反的角度研究了干扰资源优化配置问题，提出了基于最小均方误差(Minimum mean square error, MMSE)和互信息(Mutual information, MI)准则的优化算法。

MI 准则常被用在多输入多输出（Multiple input multiple output, MIMO)雷达波形设计[15-18]和功率资源优化配置[19]等问题中，用于定量表示雷达探测性能，但目前将MI 准则应用在雷达时间资源优化配置中的相关研究成果较少。本文针对有源压制干扰下的相控阵雷达时间资源优化配置问题，采用MI 准则作为目标跟踪性能的量化指标，推导了含有时间变量的雷达回波和路径增益矩阵MI 表达式，建立了时间资源优化配置模型，在最大化有效跟踪目标数的同时提高了有效目标的整体跟踪性能。仿真结果证明了本文算法的有效性。

1 系统模型

本文针对单部相控阵雷达多目标跟踪问题进行研究，且不考虑同时多波束情况。假设雷达位于( x0,y0)处且位置不变，空域中离散分布Q 个目标且数量保持不变，每一时刻雷达波束仅能照射一个目标；每个目标以初始速度( vq0,x,vq0,y)从起始位置( xq0,yq0)开始匀速直线运动。

1.1 运动模型

目标的状态转移方程可描述为

式中T 为目标照射间隔，即目标被雷达两次照射之间的时间间隔。式(1)中Wq～CN ( 0,Qq) 表示k-1时刻目标q 状态转移的过程噪声，体现状态转移过程的不确定性，其中CN 指正态分布。Qq可表示为

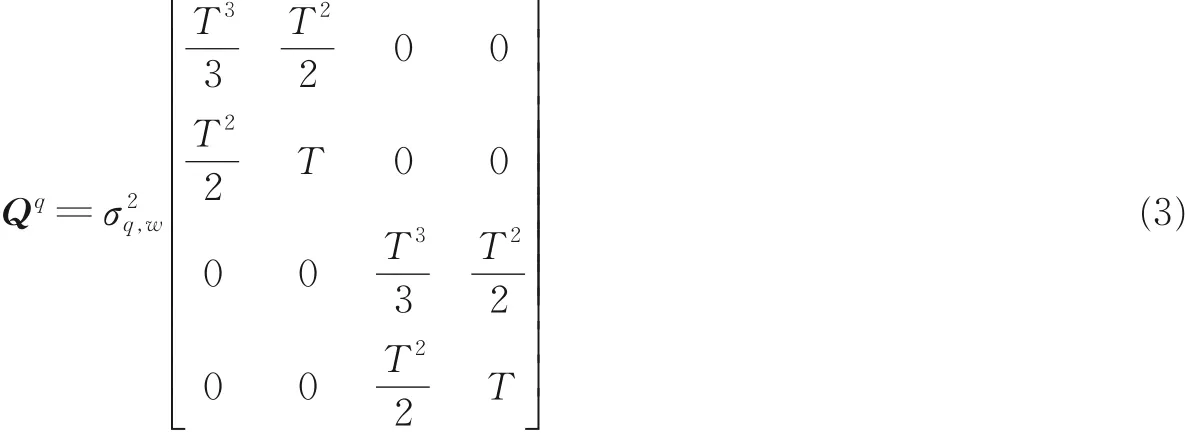
式中σ2q,w表示目标q 的状态转移过程噪声强度。

1.2 观测模型

在跟踪过程中，雷达可从回波信号中提取相应目标距离、角度、多普勒和雷达散射截面积（Radar cross section, RCS）等信息，本文考虑目标距离和角度信息。假设k 时刻雷达照射目标q，则此时刻目标

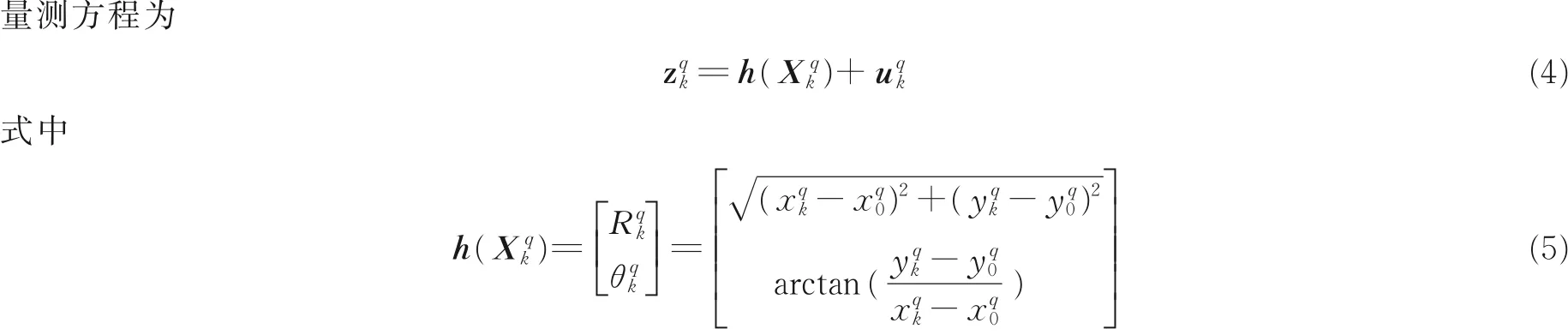
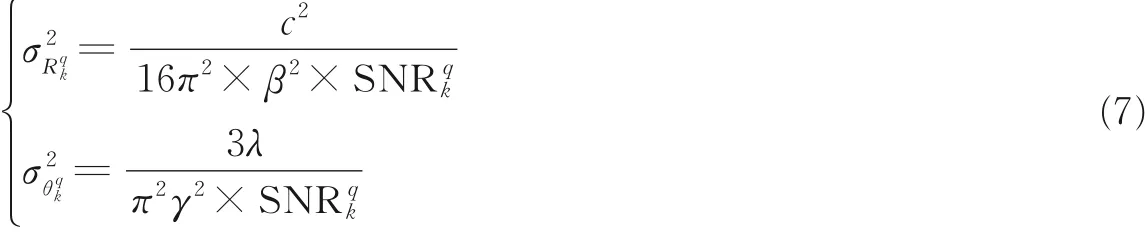
式中：c 表示光速；β 为雷达发射信号有效带宽；λ 为雷达工作波长；γ 表示天线孔径；SNRqk表示k 时刻雷达照射目标q 的回波信噪比（Signal to noise ratio, SNR）。

1.3 信号模型

在背景噪声及有源压制干扰存在时，雷达发射单个脉冲信号的回波信噪比通常无法满足目标检测和跟踪的要求，为提高回波信噪比，相干脉冲积累技术被应用到回波信号处理过程中。对于第i 个发射脉冲，雷达回波信号可表示为

式中：si为l × 1 的向量，表示发射脉冲采样；l 指采样长度；hi为路径增益系数；wi为l × 1 的接收噪声向量；ji表示l × 1 的干扰信号。

假设雷达向目标连续发射n 个脉冲，即该次探测过程的相干积累脉冲个数为n，此时回波信号为

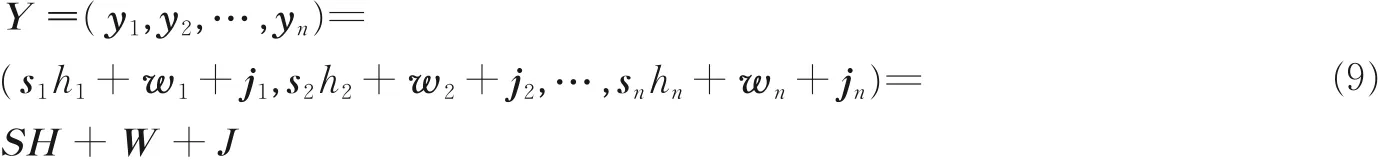
式中

且s1= s2= …= sn= s，表示发射脉冲波形完全相同。对于以上信号模型做如下假设：

(1) 雷达照射目标期间，信号传输环境保持稳定，即各脉冲间，路径增益hi独立同分布，且hi包含两个部分：目标散射系数gi和传播损耗因子pi[19]。

(2) 目标由大量小散射点组成，根据中心极限定理[21]，对于1≤i ≤n，所有gi均为独立同分布的复高斯随机变量，且满足gi～CN ( 0,σ2g)。

(3) 传播损耗因子pi是雷达天线增益和传播距离的函数，可表示为

式中：Rit和Rir分别表示目标距收发天线的距离；Gt和Gr分别表示收发天线增益，κ 为常数。

由于本文针对相控阵雷达单波束情况进行研究，收发同天线，因此有

因而传播损耗因子pi可表示为

(4) 噪声矩阵W 所有列向量是独立同分布的复高斯随机向量，且满足wi～CN ( 0,σ2wIl)，其中σ2w为环境噪声强度。

(5) 干扰矩阵J 所有列向量是独立同分布的复高斯随机向量，且满足ji～CN ( 0,σ2bIl)，其中σ2b指目标对雷达的干扰强度。

(6) 发射信号矩阵S、路径增益矩阵H、噪声矩阵W 和干扰矩阵J 均相互独立。

由假设(2)和(3)可得

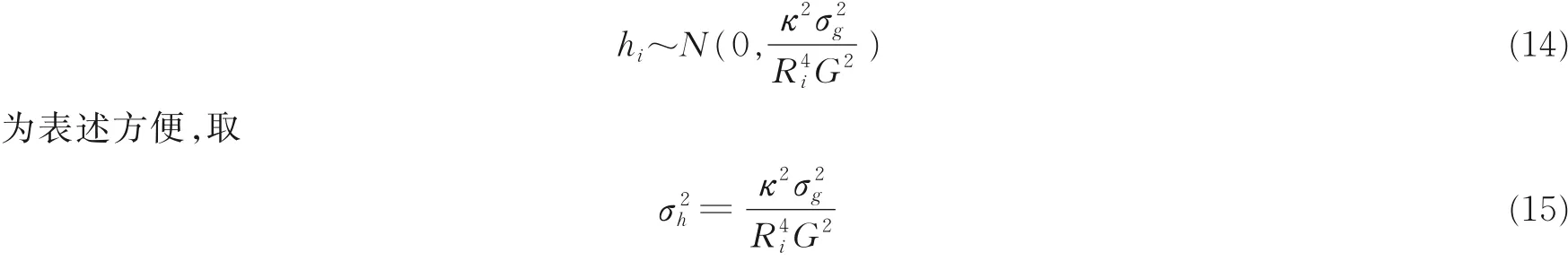
2 互信息计算

若发射信号S 已知，即发射脉冲波形s 已知，接收信号Y 与路径增益矩阵H 间的MI 可计算为[17-19]

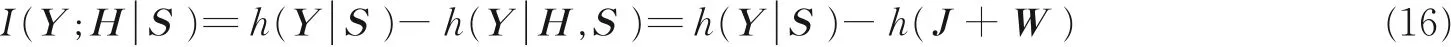
式中h( ∗)表示随机变量的微分熵。要计算I (Y ; H | S )，需要计算h(Y | S )和h( J + W )。已知发射信号S 条件下的接收信号Y 的概率密度函数为

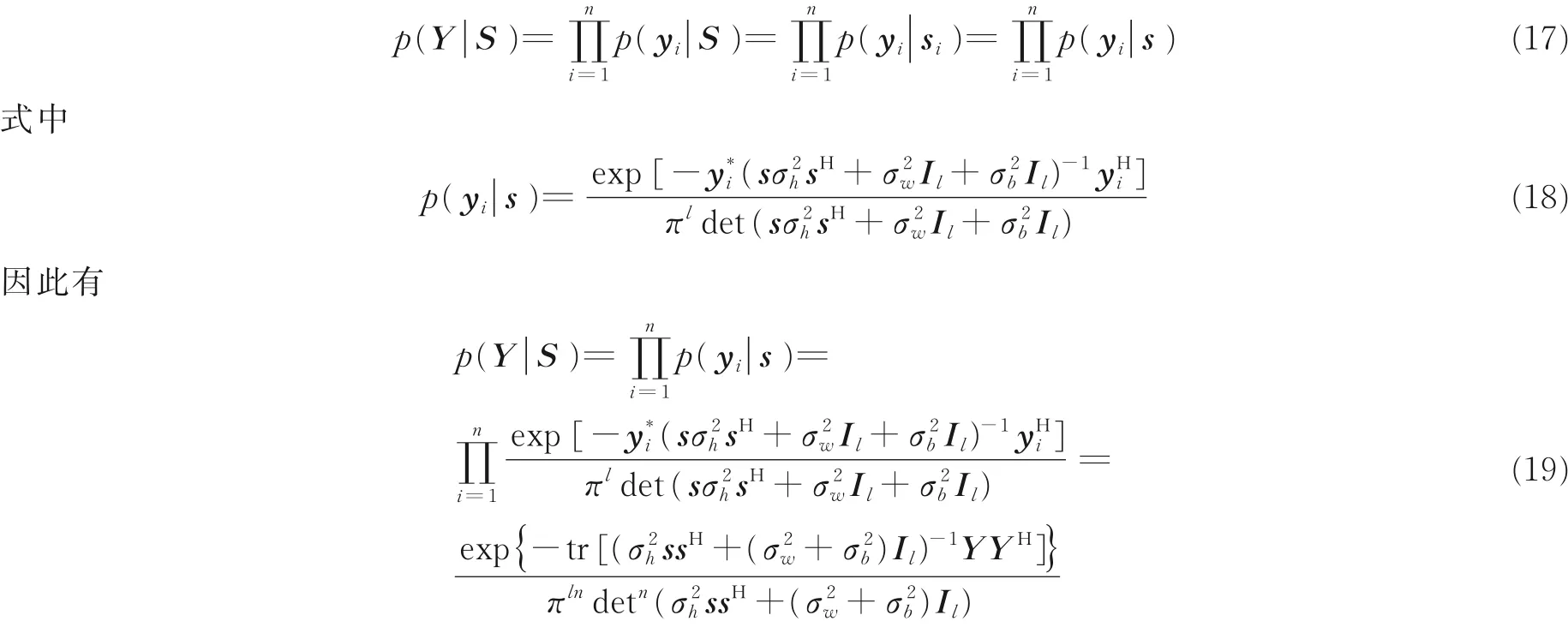
由式(19)可得条件微分熵h(Y | S )计算如下

式中MI 表示互信息量I (Y ; H | S )，是雷达发射脉冲数n 和干扰强度σ2b的函数表达式。

3 时间资源优化配置算法

3.1 跟踪性能指标

雷达回波信号与路径增益矩阵的MI 越大，目标参数估计的精度越高[15]，并且在MIMO 雷达波形设计中，最大化互信息与最小化均方误差（Mean square error, MSE)是等价的[16]，即使用MI 准则和MMSE优化得到的波形是一致的。基于上述研究成果，本文采用发射信号与路径增益矩阵MI 作为目标跟踪性能指标。根据式(23)，k 时刻雷达回波与雷达和目标q 间路径增益矩阵互信息为

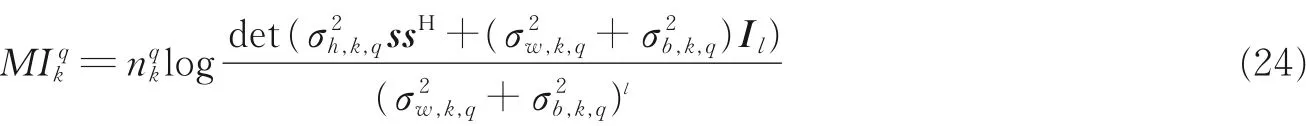
式中l 为发射脉冲采样长度。

3.2 有效跟踪目标数最大化算法

对于相控阵雷达防空应用，有效跟踪目标数是首要追求的性能指标。本文设定跟踪有效性判定准则：若不等式MIkq≥MI0成立，则判定目标q 在k 时刻被有效跟踪，其中MI0表示雷达回波与路径增益矩阵MI 的门限值。本节所提算法的功能是最大化有效跟踪目标数，该问题可用模型表示如下

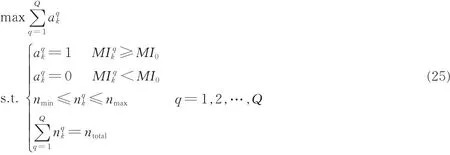
步骤1设k 时刻目标q 被有效跟踪所需的最小时间为

步骤2计算目标状态一步预测值，求得目标距雷达距离预测值Rqk，代入式(15)得到此时目标q 的冲击响应统计方差σh2,k,q，进而代入式(24)得到此时刻雷达回波与该路径增益矩阵互信息MIkq( nqk)；

步骤3令MIkq( nqk)= MI0，求解方程得到nqk_min= ceil( nqk)；

步骤4判断q 是否等于Q。若q ＜Q，则令q = q + 1，返回步骤2；若q = Q，进入步骤5；

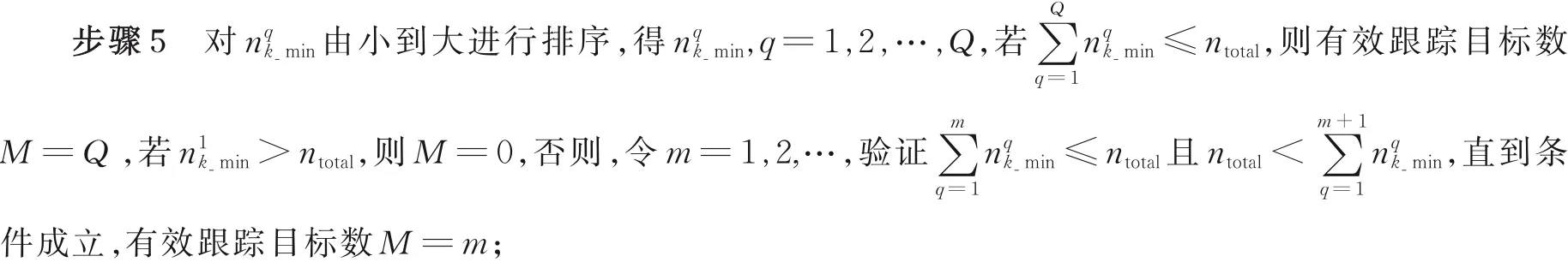
步骤6保存= 1,2,…,M，以及各时间量对应目标状态信息，M 即为下一跟踪周期雷达系统所能跟踪的最大目标数。

3.3 系统跟踪性能优化算法

由3.2 节所提算法可得到最大有效跟踪目标数以及此时各有效目标所需最小脉冲数nqk_min,q =1,2,…,M，各时间量对应目标即为下一跟踪周期将要分配资源进行跟踪的目标，记为“有效目标”，其余目标由于系统资源有限，放弃跟踪。由此可计算得到脉冲余量若nrest＞0，即脉冲余量不足以跟踪剩余目标中的任意一个，此时可将其分配给有效目标，以减小跟踪误差，实现有效目标的更精确跟踪。

本节建立资源优化分配模型，将有限的脉冲余量合理分配给各有效目标，实现系统跟踪性能优化，优化模型如下

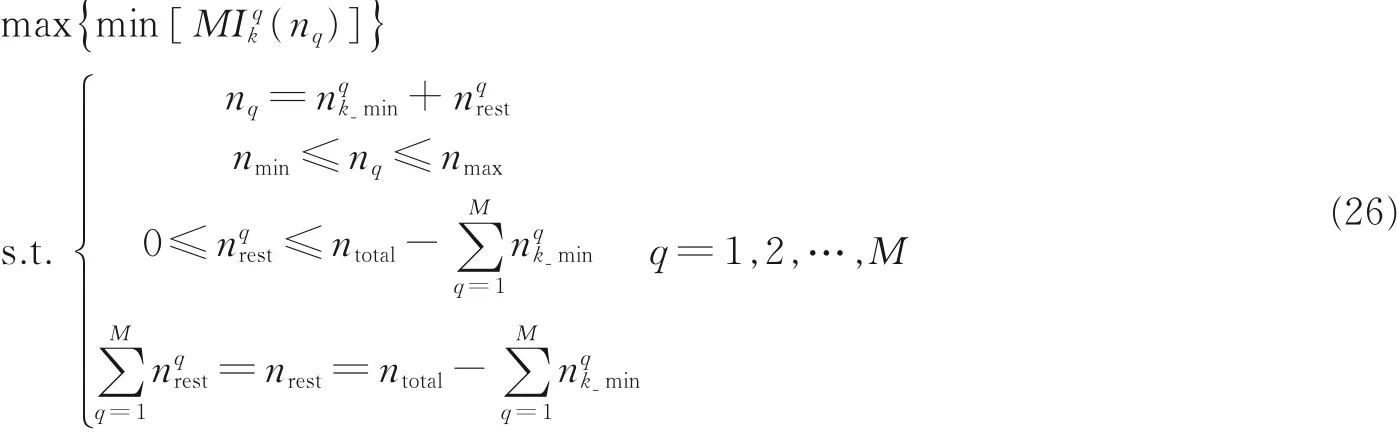
在各有效跟踪目标MI 满足门限条件下最大化最小互信息，即最优化最差跟踪目标的跟踪性能，以提高系统整体跟踪性能。其中nq为下一跟踪周期各目标分配脉冲数，MIkq( nq)表示k 时刻雷达回波与路径增益矩阵MI，计算方法如式(24)。约束条件1 表示各目标分配时间资源量是在其所需最少脉冲数的基础上开始计算的，这就保证了对于每一个被跟踪目标，= 1,2,3,…,M 成立，即各被跟踪目标分配时间资源足以保证该目标的有效跟踪；nmin和nmax分别为雷达照射目标驻留脉冲数的下限和上限；nqrest表示目标q 分配所得脉冲余量，约束3，4 对其进行了限制和说明，进而保证了

针对式(26)中的优化模型，由于优化变量是脉冲个数，为离散变量，因此该优化问题是非凸的。针对该问题，本文选用改进的遗传算法进行求解，算法流程如下：

步骤1初始化种群。若下一跟踪周期有效跟踪目标数M，则每个个体的染色体长度为( M - 1)×Ns，随机产生Np 条染色体，其中Ns 表示个体基因长度，满足精度要求，Np 表示种群大小，记代数g = 1；

步骤2交叉、变异。根据预定的交叉概率和变异概率进行交叉、变异操作，更新染色体；

步骤3计算每条染色体对应的目标函数值，此处为有效目标最小互信息；

步骤4使用轮盘赌方法对种群中个体进行选择；

步骤5令g = g + 1，判断g ＞Ng 是否成立，若是，进入步骤6，否则，返回步骤2；

步骤6计算种群中各条染色体对应的目标函数值，选择目标函数值最大的个体输出，并返回下一跟踪周期各有效目标时间分配方案nqk,q = 1,2,…,M。

3.4 多目标跟踪策略

对于本文研究的多目标跟踪问题，由于各目标在空间中离散分布，因此可将其简化为多个单目标跟踪问题。扩展卡尔曼滤波(Extended Kalman filtering，EKF)是解决非线性滤波问题的常用方法，性能可靠。由于式(5)所示的观测模型具有非线性特征，因此本文选取该方法对目标状态进行估计。

结合本文所提资源优化配置算法，目标跟踪策略可简述为：首先，结合k 时刻探测到的各目标干扰强度和当前各目标状态信息，采用有效跟踪目标数最大化算法获得下一跟踪周期待跟踪目标和各目标有效跟踪所需最小脉冲数nqk_min，然后在此基础上调用系统跟踪性能优化算法得到有效目标时间资源分配方案nqk，指导雷达对各目标进行照射跟踪，之后采用EKF 算法对各目标回波进行滤波，获得目标状态估计值。多目标跟踪策略流程如图1 所示。

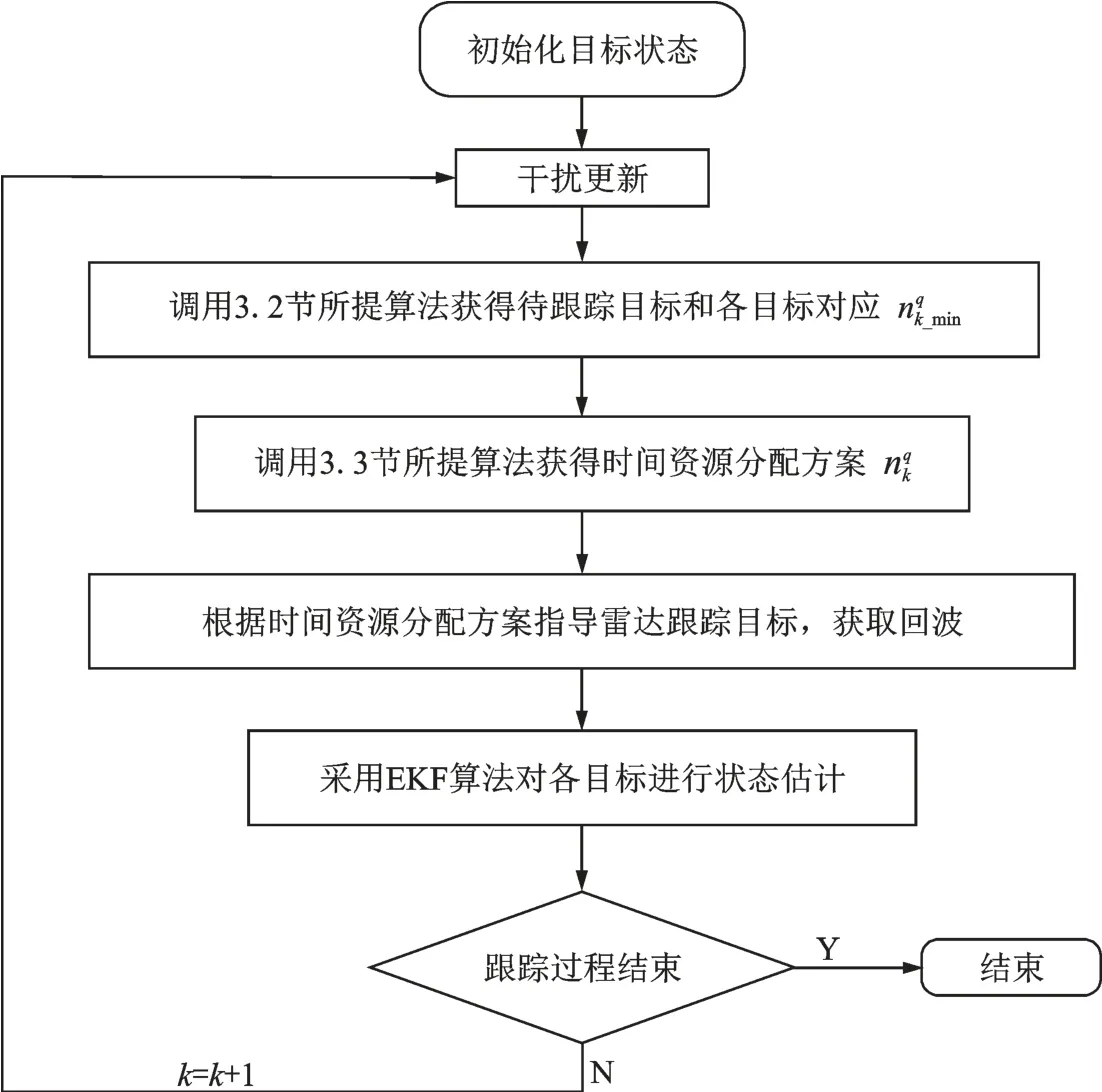
图1 多目标跟踪策略流程图Fig.1 Multi-target tracking strategy flowchart

4 仿真结果与分析

4.1 仿真参数

为验证本文所提算法的有效性，本节设计了仿真实验进行验证。实验场景下空域离散分布Q = 8个目标，各目标携带干扰机，如图2所示。干扰强度变化情况如图3 所示，一部相控阵雷达分时对各目标进行跟踪。为简化计算，取噪声强度σ2w= 1，目标散射特性σ2g= 1，发射信号码长l = 5；实验中一个跟踪周期总时间跨度Ttotal= 3.2 s，发射脉冲周期PRI = 10-3s，因此一个跟踪周期包含ntotal= 3 200 个脉冲；采样间隔T = 5 s，雷达照射目标驻留时间的下限和上限分别为：nmin= 0.005ntotal和nmax= 0.8ntotal；雷达增益Gt= Gr= 33.5 dB；遗传算法迭代次数Ng= 100，种群大小为Np= 100，交叉和变异概率分别为0.6 和0.005；互信息门限MI0= 0.8 b。实验参数如表1 所示。

为更直观体现目标跟踪性能，本文计算了各目标跟踪均方根误差(Root mean square error, RMSE)，计算方法为

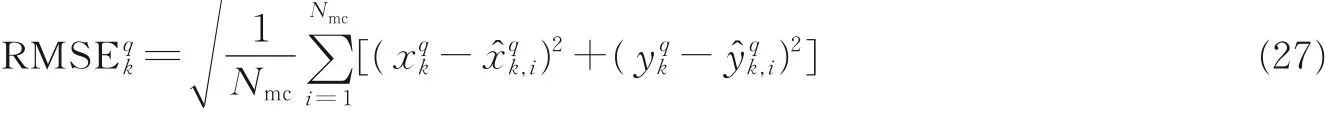
式中Nmc为蒙特卡洛仿真次数，实验中取Nmc= 500；(xqk,yqk) 为目标的真实坐标，(x̂qk,i,ŷqk,i)为第i次蒙特卡洛仿真中得到的目标坐标估计。

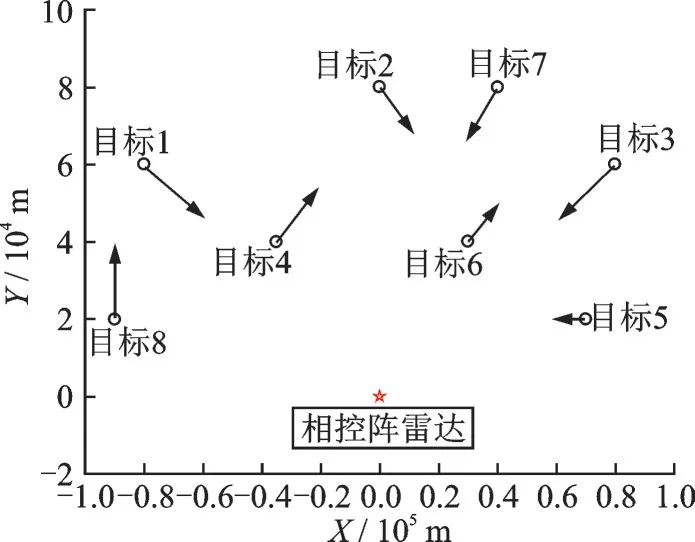
图2 雷达及目标分布图Fig.2 Radar and target distribution map

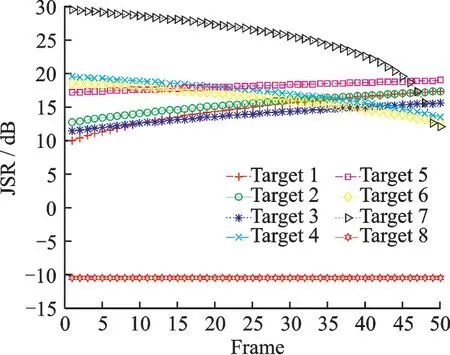
图3 目标干扰强度Fig.3 Target jamming intensity

表1 目标参数Table 1 Parameters of targets

为体现本文所提资源分配算法的有效性，采用平均分配方案进行对比，即每一帧对各目标平均分配时间资源，各目标分配脉冲数均为naverage=ntotal/Q= 400 个；与此同时，在相同条件下以目标跟踪距离误差贝叶斯克拉美罗下界(Bayesian Cramer-Rao lower bound, BCRLB)作为目标跟踪性能量化指标(以下称为BCRLB 指标)，进行了实验验证，进一步证明以MI 作为目标跟踪性能量化指标的有效性。仿真共进行50 帧。

4.2 结果与分析

干扰条件下，尽可能多地有效跟踪目标是雷达系统的首要和基础任务。如图4 所示，平均分配方案跟踪过程中，在第15 帧附近出现了有效目标数减少的情况，这是由于4 号和6 号目标远离雷达飞行，超出一定范围后目标失踪；跟踪过程出现有效目标数增加的情况则是由于多数目标靠近雷达飞行，并且本文所提优化方案总是能够提前于平均分配方案对靠近目标进行稳定有效的跟踪；相比于平均分配方案，本文所提算法在相同时间资源的条件下总是可以有效跟踪更多的目标。

图5 所示为相同条件下BCRLB 指标有效跟踪目标数随时间的变化情况，相比平均分配方案，其提高幅度并没有整体超过30%，MI 指标有效跟踪目标数提高50% 以上。

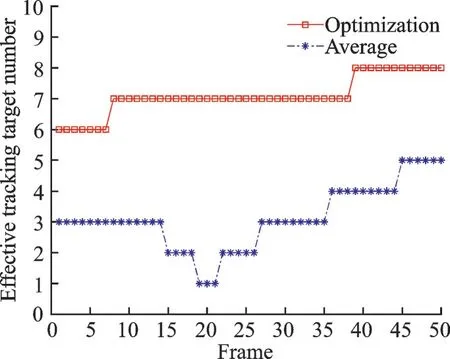
图4 有效跟踪目标数(MI 指标)Fig.4 Effective tracking target number (MI)

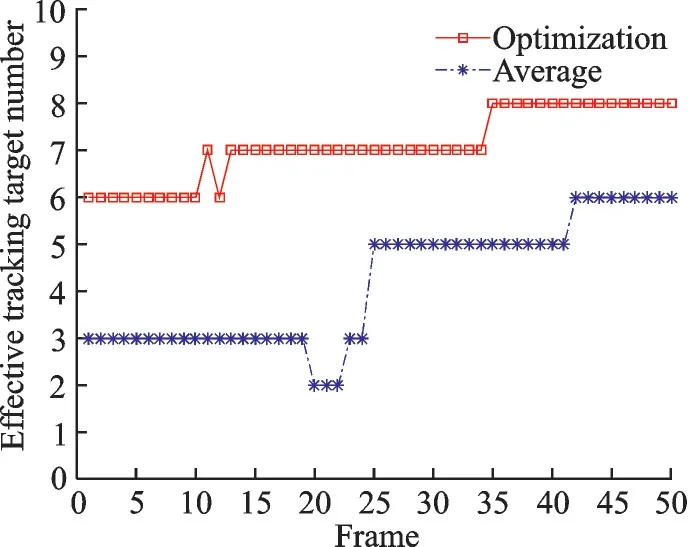
图5 有效跟踪目标数(BCRLB 指标)Fig.5 Minimum MI of effective targets (BCRLB)

为进一步体现对剩余脉冲优化分配的效果，本文建立了一步优化方案进行对比。所谓一步优化方案，即对剩余脉冲数进行平均分配。图6 给出各方案下有效目标最小互信息变化情况，相比于平均分配方案，优化方案最小互信息始终保持在门限MI0= 0.8 b 以上，这保证了有效目标的跟踪有效性。相比于一步优化方案，最终优化结果有效提高了最小互信息量。图中第8 帧和38 帧出现最小互信息大幅下降，这是由于8 帧和38 帧处有新目标被纳入有效目标范围，绝大部分剩余脉冲被新的有效目标占用，因而最小互信息回到门限值附近，有效目标数的增加可从图4 中得到证实。对于平均方案最小互信息在38 帧附近出现陡降，这也是由于38 帧附近有新目标被纳入有效目标，该目标是7 号目标，由于其干扰强度在40 帧附近开始快速下降，因而40 帧附近3 种方案下最小互信息都出现快速上升。

图7 显示了各方案下有效目标最大RMSE 变化情况，相比于平均方案，优化方案有效目标最大RMSE 明显降低。对比图7 与图6，可以判定MI 与RMSE 反相关，即对于一个给定目标，MI 越小则RMSE 越大，这与直观判断也是一致的：回波中包含目标的信息越少，跟踪精度自然越低。对于MI 与RMSE 的定量关系，本文暂不能给出，这将是作者接下来试图解决的问题。

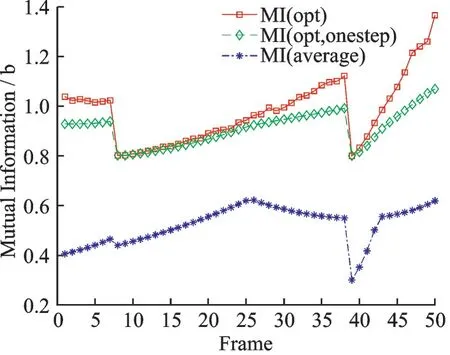
图6 有效目标最小互信息Fig.6 Minimum MI of effective targets

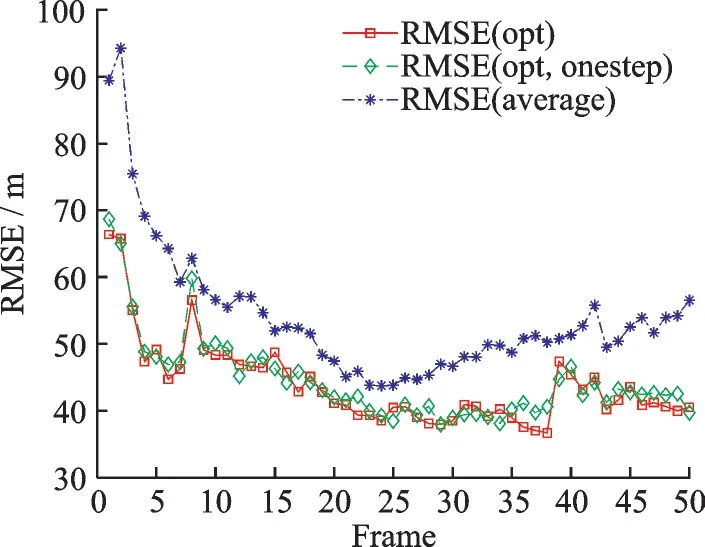
图7 有效目标最大RMSEFig.7 Maximum RMSE for effective targets

图8 中，对于有效目标平均RMSE，MI 指标下3 种方案中一步优化方案性能最优，而最终优化方案与平均方案性能基本一致，这是由于最终优化方案将大部分剩余脉冲分配给跟踪性能最差的有效目标，而该目标由于干扰较大或距离较远的原因，跟踪精度随脉冲数提高缓慢。最终优化方案提高了跟踪性能最差目标的跟踪精度，对有效目标的跟踪性能起到整体提升的效果。

图9 所示是相同条件下BCRLB 指标有效目标平均RMSE 随时间的变化情况，可以看到与MI 指标一样，BCRLB 指标下的有效目标平均RMSE 也随时间逐步降低，证明了该指标的有效性。但与MI 指标相比，图9 中35 帧之前各方案下有效目标平均RMSE 都在40 m 以上，而图8 中对应时间段的有效目标平均RMSE 基本小于40 m，MI 指标下的方案对有效目标的跟踪性能的整体提升效果更为明显。

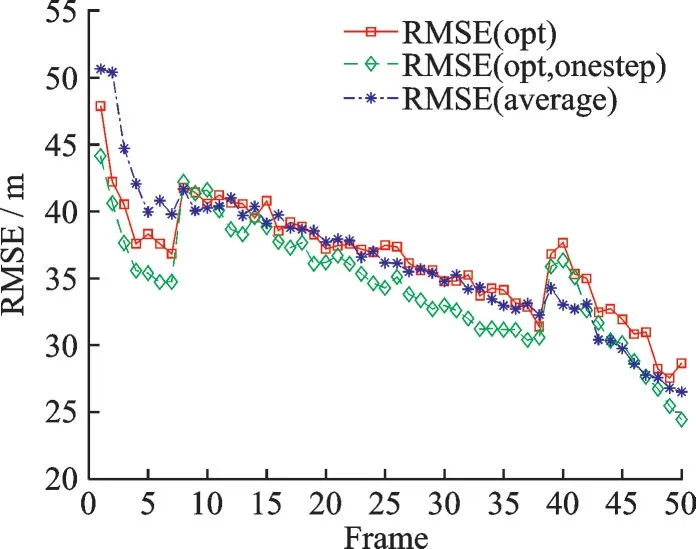
图8 有效目标平均RMSE(MI 指标)Fig.8 Average RMSE of effective targets (MI)

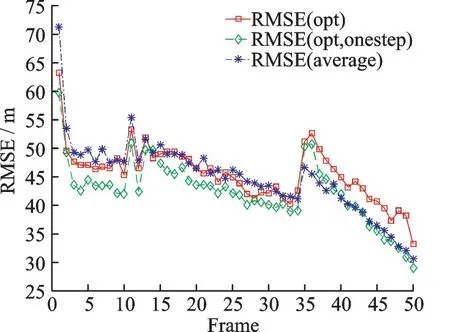
图9 有效目标平均RMSE(BCRLB 指标)Fig.9 Average RMSE of effective targets (BCRLB)

图10 和图11 分别显示了最终优化方案和一步优化方案时间资源分配结果，可以看到相比于一步优化方案，最终优化方案各目标被分配时间资源差距更明显。具体而言，6 号目标互信息在多数帧下最小，因而更多的剩余时间资源被分配给6 号目标，实现最小互信息最大化。

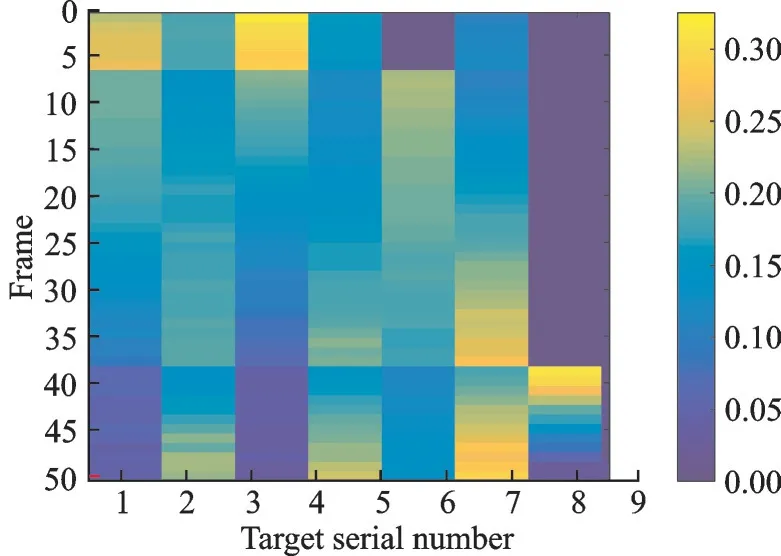
图10 时间分配方案Fig.10 Time allocation scheme

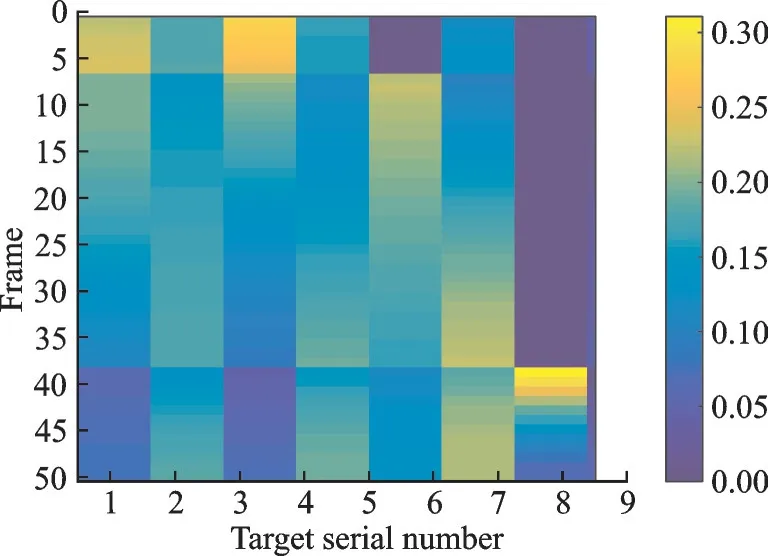
图11 时间分配方案（一步优化）Fig.11 Time allocation scheme (onestep opt)

5 结束语

本文针对有源压制干扰下的相控阵雷达多目标跟踪时间资源优化配置问题，将MI 准则引入并用作目标跟踪性能的量化指标，推导了包含驻留脉冲数的雷达回波与路径增益矩阵的互信息表达式，针对时间资源分配问题建立优化模型，并采用改进的遗传算法进行求解。仿真结果证明，本文所提时间资源优化配置算法可在实现有效跟踪目标数最大化的同时，显著提高有效目标中跟踪性能最差目标的跟踪精度，从而提高了有效跟踪目标的整体跟踪效果。