一种快速搜索模糊函数主脊切面的自适应灰狼算法

郑陵潇，吴海潇，陈 磊，普运伟，

（1.昆明理工大学计算中心，昆明，650500；2.昆明理工大学信息工程与自动化学院，昆明，650500）

引 言

在现代战争中,更加先进与复杂的雷达系统不断地被投入使用，使得实际电磁威胁环境较过去已经发生了很大的变化。传统辐射源信号的分选主要依赖于经典5 参数[1-4]进行，但由于现代雷达信号的脉冲流多变、快变且在高密度环境中易交叠，分选的效果大大降低。因此，构建科学完备的特征参数信息在电子侦察对抗领域中有着重大的战略意义。

近年来，人们普遍认识到脉内特征作为辐射源信号所特有的一种调制特征，可在一定程度上提高分选识别准确性。典型的脉内特征包括：符号化特征[2]、基于盒维数和稀疏性的复杂度特征[5]、小波包变换特征[6]、双谱二维特征[7]、熵特征[8]、相像系数[9]等。但是，基于这些脉内特征的分选方法基本上仅局限于部分调制信号，缺乏普遍性，且在一定程度上存在对噪声敏感的缺点。

为了从信号分选的角度和普遍意义上去提取和研究信号的脉内特征，文献[1]提出了一种模糊函数主脊（Ambiguity function main ridge，AFMR）切面特征提取方法。该方法通过分数自相关（Fractional autocorrelation, FA）搜索AFMR 切面，并采用矩方法描述该切面的特征分布信息来提取特征参数。实验结果表明，所提取的特征向量具有较好的噪声稳健性和聚类效果。但由于文献[1]采用的是穷举搜索法，其搜索需经过计算密集，降低了该方法的实用性。因此，可采用更有效的智能算法快速精确地搜索AFMR 切面。

本文在标准灰狼优化算法的基础上，提出了一种新的自适应灰狼算法来搜索AFMR 切面并提取切面特征。实验结果表明，与文献[1]和标准灰狼优化算法相比，本文方法在提高搜索效率的同时获得了更加真实的主脊切面，并且具有更优的噪声鲁棒性。

1 提取AFMR 切面特征

模糊函数（Ambiguity function，AF）本质上是为信号的自相关函数进行傅里叶变换，其定义为[1]

式中，τ 为时延，ξ 为频移，反映了雷达信号在二维平面的相似度关系，s( t )为窄带雷达信号。

文献[10]定义了FA 运算，为提取AF 的径向切面提供了一种简洁、快速的方法[4]，具体公式为

式中，Cp是旋转角为 α 的分数域 μα上的分数自相关算子，ρ 为 μα域的径向距离，χs为信号模糊函数。式（2）表明，旋转角为α 的分数域的自相关等价于该分数域上模糊函数的径向切面[1]。因此,通过计算信号的FA 而得到AF 任一过原点的径向切面[4]。

在不同调制参数下，AF 的能量分布波形也会有所差异，同时这种差异会反映在信号的AFMR 切面上。因此，提取该类切面的表征参数，对辐射源信号的分选至关重要。鉴于AF 的能量分布带具有局限性及高度对称性，可将AFMR 切面的角度搜索范围限制在（-π/2,π/2），并对旋转角α 作径向积分，构建如下的检测量

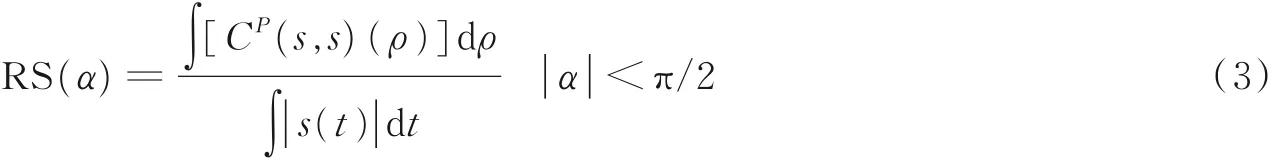
式（3）中，将分母的值限定为在[0,1]之内的随机数，目的是减少噪声和信号能量对RS( α )取值范围的影响[1]。根据检测量RS( α )可得到AFMR 切面，同时也可给出相应的3 个主脊切面特征向量。

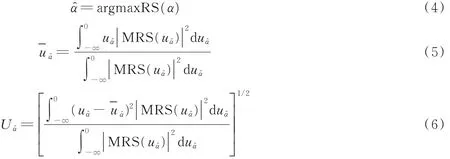
2 搜索AFMR 切面的自适应灰狼算法

灰狼优化算法（Grey wolf optimization algorithm，GWO）是受狼群协同捕食活动启发而提出的一种算法更新机制[11]。GWO 具有较优收敛性能、较强的全局搜索能力和较高的适应性等特点。灰狼优化算法广泛应用于PI 控制器参数[12]、模块化粒状神经网络设计[13]、分布式压缩感知问题[14]、多目标权衡的框架搭建[15]和粒子滤波器优化[16]等领域。

社会等级关系严格支配着灰狼种群，所以设计GWO 时需按照种群中个体适应度的优劣性，构建α、β、δ 和ω 四个社会等级层次模型。最高等级的狼为头狼α，α 狼主要负责对群体事务活动做出决策，在群体中占有主导地位。其他的狼需要服从α 狼的命令。第2 等级的狼称为β，它服从α 狼的指令并协助其工作，是最高决策层与下级被支配层的重要纽带。第3 等狼称为δ，它服从α 、β 狼，同时支配剩余层级的狼。处于底层的狼称为ω 狼，它通常需要服从其他社会层次上的狼并对猎物进行围攻，是整个群体中数量最多的狼。

狼群捜索猎物时会逐渐地接近并包围它，该过程的数学模型如下

式中，D 为灰狼与食物的间隔，Xp为猎物的方向矢量值，X 为经t 次迭代后灰狼的位置，t 为迭代次数[17]。C 与A 为协同系数因子，其计算公式为

r1与r2为[0,1］之间的随机向量。a 被称为收敛因子，在整个迭代过程中a 由2 线性减小至0。其中，nMax_iter为算法的最大迭代轮数。如式(11)所示

灰狼具有识别潜在猎物位置的能力，GWO 的优化过程主要由每代种群中最优的3 个解（即α、β、δ）来指导完成。但在多维空间中，灰狼无法精准识别猎物的具体位置。因此算法会对每次迭代后的个体进行评价比较，根据结果重新保留α、β、δ 的位置信息。种群中的其他个体会在它们的指引下逐步向猎物逼近、包围直至成功捕获。此阶段位置更新的具体公式如下

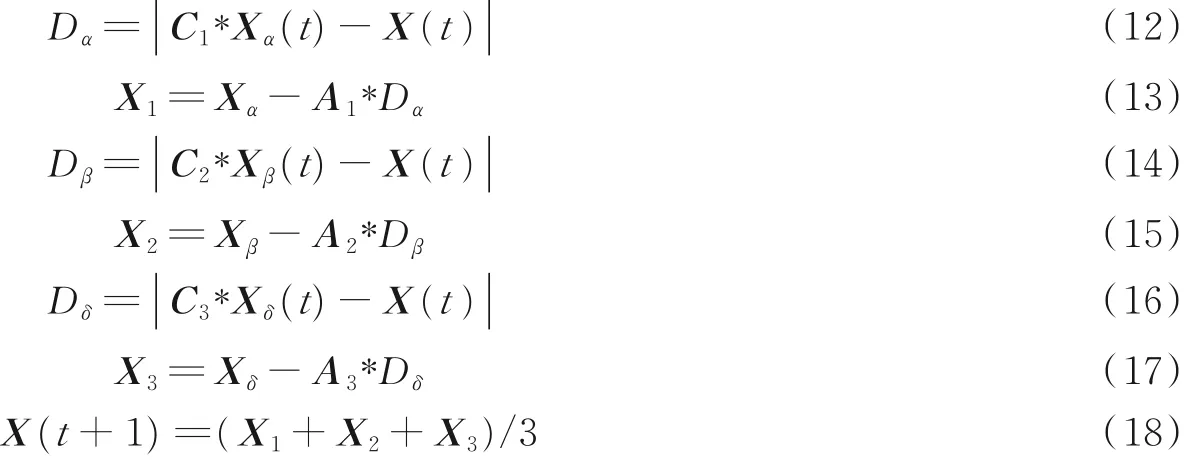
式中，Xα，Xβ，Xδ分别表示α，β，δ狼的位置，Dα，Dβ,Dδ分别表示当前候选灰狼与最优3 条狼之间的距离；X(t)表示灰狼的位置。

算法中动态信息的更迭，主要通过式(11)中收敛因子的递减来实现的，同时收敛因子也影响着A向量变化，A值控制着灰狼个体向猎物逼近的距离。当|A|＞1 时，灰狼分散在各区域搜寻猎物。当|A|＜1 时，灰狼会集中某一区域内搜寻猎物。由式(10)可知另一个搜索向量C是在[0,2]上的随机数，为灰狼搜索提供了阻碍。这种行为机制可避免灰狼快速地聚拢在某一局部，有助于减缓迭代过程中的提前收敛现象。其搜索过程如图1 所示。

2.1 均匀初始化

在灰狼优化算法中，采用随机初始化方法虽简单，但一开始所有的可行解呈不均匀分布状态，造成算法收敛速度慢，不利于问题的快速求解。为避免以上缺点，可采取均匀初始化方法。 由式（3）可知，RS(a)的自变量范围在（-π/2，π/2）之间。在低维度且种群数量较少的问题中，可将a值均分为20 等份，去除干扰性强的2 个边界点后，取中间值和一个随机点作为初始灰狼值。这样就可以使候选解呈均匀分布状态，从而加快算法的搜索速度。2 种初始化种群的方法如图2 所示。

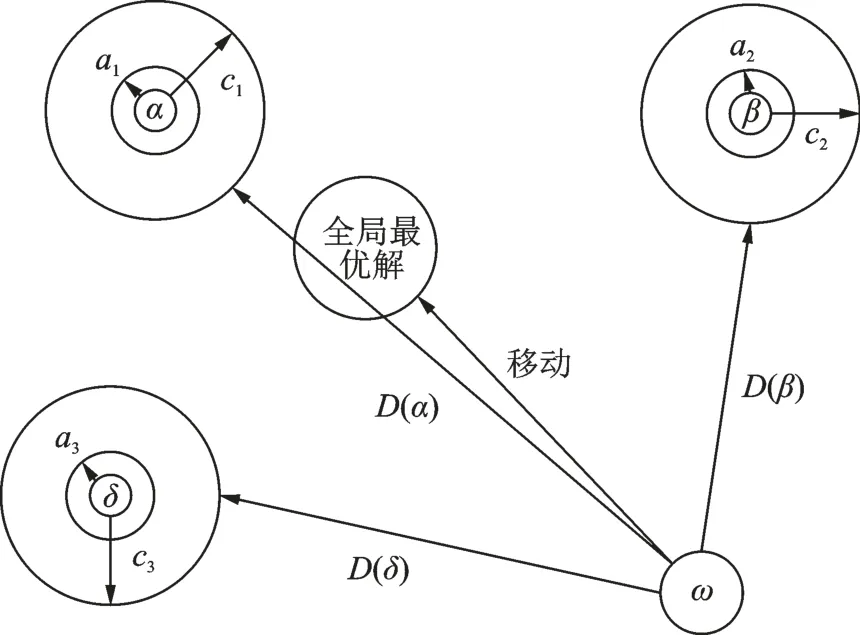
图1 灰狼种群搜索时位置更新原理图Fig.1 Schematic diagram of position update during grey wolf population search

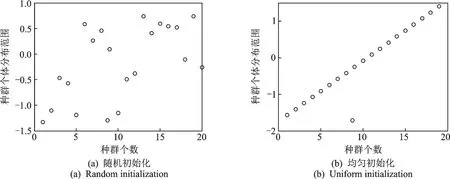
图2 随机初始化灰狼种群和均匀初始化灰狼种群的个体分布示意图Fig.2 Random initialization and uniform initialization of grey wolf population

2.2 改进的非线性收敛因子

在标准灰狼优化算法中，收敛因子a的变化影响着算法性能的优劣。但在实际优化过程中搜索并非呈线性状态，这在一定程度上限制了算法优化。因此本文提出了一种基于幂指型函数的改进非线性收敛因子，具体公式为

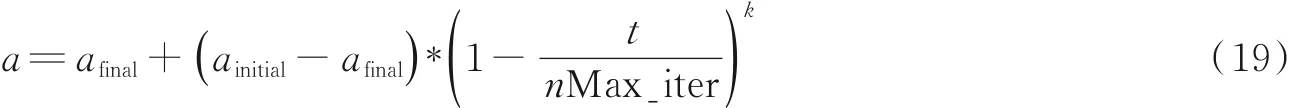
式中,afinal为终止值，取值为0；ainitial为初始值，取值为2。k为调节指数，a在不同k值下的非线性动态变化如图3所示。

由 图3 可 知 ，k=2 时 ，曲 线 从90 代 开 始 收 敛 ；k=3时，从85～90 代开始收敛；k=4 时，明显出现早收敛现象；而k=10 时，早收敛更为明显，极易陷入局部最优。故选择k为2 或3 均可，本文实验中均取k值为3。在搜索初期，改进收敛因子的衰减速率较原始收敛因子的快，提高了算法的搜索速度，增强了灰狼种群的勘探发掘能力，可快速定位到有效的解空间；在搜索后期，随着改进a值的衰减速率降低，灰狼可在小范围内进行精细搜索，提高了算法的局部搜索精度，平衡了进程的动态寻优，进而保证了狼群在全局的勘探和局部范围内的精细搜索能力。

2.3 自适应种群更新策略

在标准灰狼优化算法中，灰狼的搜索及攻击行为依赖于前3 层狼的优化过程而非个体之间的共同交互信息。此方式虽能在GWO 算法前期快速搜索到有效解空间，但在算法后期，随着迭代次数增加，当1＜|A|≤2 时，狼群中所有个体向决策层区域逼近，不再靠近猎物范围内搜寻，算法容易提前收敛，陷入局部最优。另外，由式（18）可知，通过求解α、β和δ狼的位置的动态均值来确定权重，以此来更新子代个体的位置信息。但此方法不能保证子代个体的随机性，降低了搜索准确率。

为保证狼群搜索的多样性，避免算法陷入局部最优，本文对灰狼种群的位置更新做出了变异性操作。即将遗传算法（Genetic algorithm，GA）中遗传与变异算子引入到原有的更新方法中，使灰狼种群能够自适应调整变异位置，产生新的子代个体能够保留较优的位置或者变异较差的位置。即将当前个体的适应度值fi与灰狼种群的平均适应度值favg进行比较。如果fi小于favg，则说明迭代后个体保留了较差的变异结果，这时可适当让该个体远离种群的较优解，逃逸出局部最优现象；若相反，则表示迭代后个体具有更优变异值，此时需逐步缩小子代与优秀个体的距离。具体公式如下

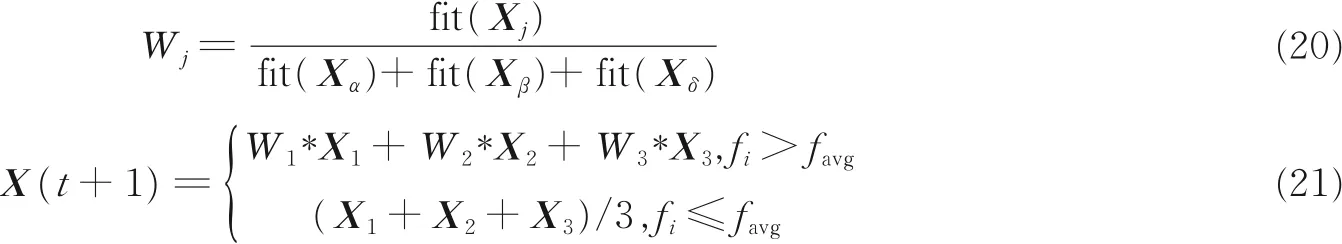
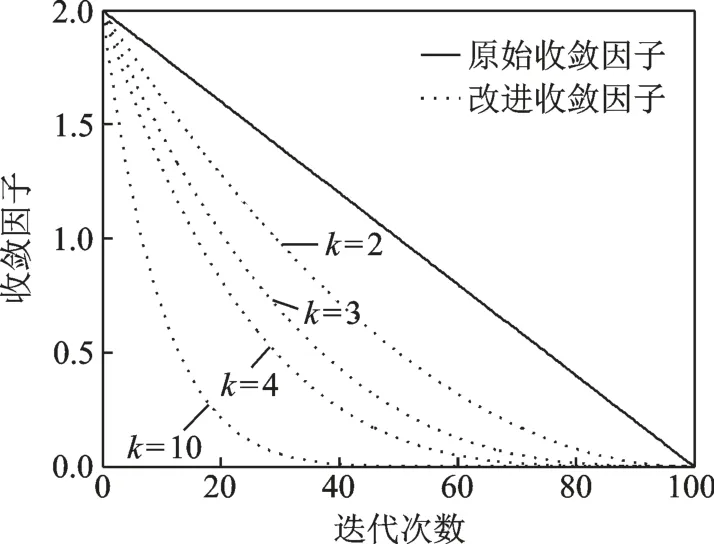
图3 收敛因子a、调节指数k 与收敛代数的关系Fig.3 Relationship between convergence factor a, regulation index k and convergence algebra

综上所述，改进GWO 搜索并提取AFMR 切面特征值方法可概括为图4 所示。

3 实验结果及分析

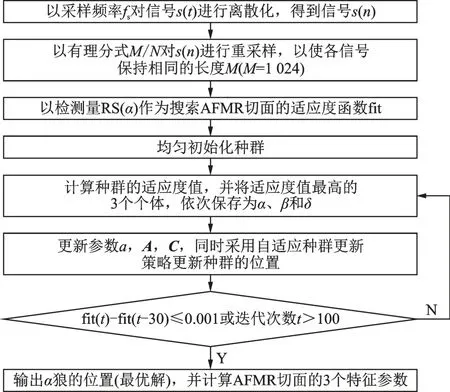
图4 本文算法流程图Fig.4 The flowchart of the algorithm

选取与文献[1]各种参数相同的信号如下：常规脉冲信号（Conventionality pulse, CON）、线性调频信号（Linear frequency modulation,LFM）、二相编码信号（Binary phase shift keying，BPSK）、四相编码信号（Quadrature phase shift keying，QPSK）、M 序 列 信 号（M - Sequence, MSEQ）、二进制频移键控（Binary frequency shift keying，BFSK）[3]。设定种群数量为20，最大迭代次数为100。 运行环境为3.60 GHz 处理器,8.00 GB 内存的计算机，仿真软件为Matlab R2014a。各实验分别进行100次随机测试。

实验1设置信噪比（Sound-to-noise ratio, SNR）为20 dB，在此条件下，每种调制类型各随机产生100 个初始信号。分别利用文献[1]方法、标准GWO 和本文方法对AFMR 切面进行搜索并提取α̂、-u α̂、Uα̂。比较其时耗、切面值RS(α)和收敛代数。其中时耗为依照图4 流程所示的单个信号运行所用的时间[18]。平均搜索耗时、切面值RS(α)的大小和平均收敛终止代数分别列于表1—3。图5 则给出BPSK 信号、M-SEQ 信号和QPSK 信号在标准GWO 和改进GWO 下的收敛过程。图6 为上述3 种方法随机某次搜索到的6 种信号的AFMR切面对比图。

由表1 可知，在搜索6 种典型辐射源信号的AFMR 切面并提取切面特征时，穷举法平均耗时为6.13 s，标准GWO 平均耗时为1.84 s，而改进GWO 的平均耗时仅为1.49 s，搜索效率分别提高了75.7% 和19.0%。此外，由表2 可知，采用标准GWO 与改进GWO 搜索到的RS(α)的值均大于文献[1]的搜索结果，效率平均提升了4.3% 和4.9%。这说明标准GWO 与改进GWO 在具有更快搜索速度的同时，也搜索到了更加真实的AFMR 切面。

表1 AFMR 切面特征提取耗时对比Table 1 Time comparison of AFMR slice feature extraction s

表2 切面值RS（α）的搜索对比Table 2 Search comparison of slices RS（α）

表3 的结果进一步说明了改进GWO 和标准GWO 在时效性方面的对比情况。具体来讲，改进GWO 对6 种信号的平均收敛终止代数为36.4代，即平均每次搜索到AFMR 切面时需要搜索728 次（36.4 乘以种群的数量20），标准GWO 需要搜索770 次，对比文献[1]的穷举法，每次需要搜索1 800 次，其运算量大大减少，搜索AFMR 切面的效率分别提高了59.6% 和57.2%。

此外，图5 显示出，改进GWO 的收敛效果明显优于标准GWO，且改进GWO 的收敛曲线中较少地出现“平台曲折”的现象，有利于算法跳出局部最优。图6表明，3种方法搜索BPSK 信号、M-SEQ 信号、QPSK 信号的AFMR 切面基本一致，说明本文方法理论上可行。而对于其余的3种信号，标准GWO 和本文方法明显能得到更精确的搜索结果。

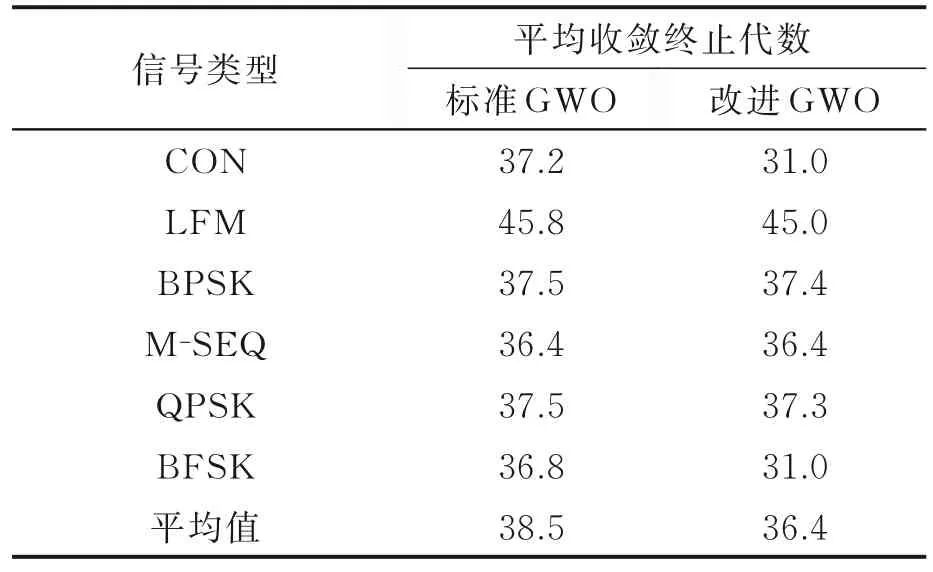
表3 标准GWO 与改进GWO 的平均收敛终止代数Table 3 Average convergence termination algebra of standard GWO and improved GWO

图5 SNR=20 dB 时3 种信号在标准GWO 和改进GWO 下的收敛过程Fig.5 Convergence process of different signals under standard GWO and improved GWO at SNR=20 dB

实验2设置SNR 分别为0、5、10、15、20 dB，在此条件下，每种调制类型各随机产生100 个初始信号。 分别利用文献[1] 方法、标准GWO 和本文方法搜索此信号集所有信号的AFMR 切面并提取α̂，-u α̂，Uα̂。

表4 给出了采用MATLAB 自带的FCM（模糊K 均值聚类）算法对3 种方法所提取到特征值的聚类结果。图7 示例性地给出了改进GWO 提取到特征值的三维分布情况，图中同一种信号用相同形状的图形表示。

由表4 可知，3 种方法所提取到特征值的聚类准确率在SNR 不低于5 dB 时都达到100%。但在5 dB 以下时，穷举法与标准GWO 的聚类准确率相当，而改进GWO 的聚类准确率略高。这说明即使在低SNR 环境下，采用标准GWO 和改进GWO 搜索并提取信号的AFMR 切面特征是可行和有效的，而且改进GWO 在面对噪声的影响时显示出了更好的稳定性。

图7 进一步显示出，采用改进GWO 能较好地分选6 类信号，尤其是当SNR≥5 dB 时，搜索并提取到的AFMR 切面特征值具有良好的类内聚敛性和类间分离性。即使SNR=0 dB 时，也只存在较小的混叠现象。SNR 为15 dB 和20 dB 的情况和图7 中(c)类似，不再给出。

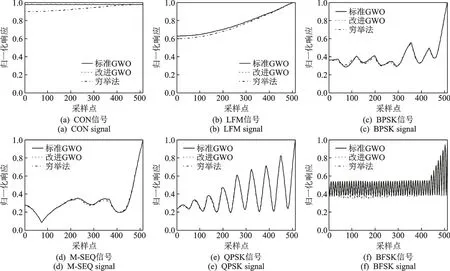
图6 SNR=20 dB 时6 种信号的AFMR 截面图Fig.6 AFMR cross-section of various signals at SNR=20 dB

表4 固定SNR 下3 种方法提取到特征值的聚类准确率Table 4 Clustering accuracy of three methods for extracting eigenvalues at a fixed SNR

图7 改进GWO 在不同SNR 下提取到AFMR 切面特征值的分布Fig.7 Distribution of eigenvalues of AFMR slices extracted by improved GWO at different SNRs

实验3 使SNR 在0～20 dB 内每隔5 dB 进行动态变化并对每类信号随机抽取20 个样本，组成SNR 变化的样本容量为600 的测试信号集。分别利用文献[1]方法、标准GWO 和本文方法搜索此信号集 所 有 信 号 的AFMR 切 面 并 提 取图8 给 出 了3 种 方 法 提 取 到 特 征 值 的 三 维 分 布 情 况 。 表5—7 给出了FCM 算法对所提取特征值的聚类结果。

由图8 可见，采用标准GWO 和改进GWO 提取到切面特征值的分布情况与采用穷举法提取到的切面特征值的分布情况基本一样，从而证明了当SNR 变化时，采用标准GWO 和改进GWO 搜索并提取信号AFMR 切面特征的可行性和正确性，而且采用改进GWO 提取到切面特征值的类内聚敛性和类间分离性更好。表5—7 分别给出了3 种方法的聚类准确率。穷举法、标准GWO 和改进GWO 对6 种信号的平均聚类准确率分别为94.8%、94.3% 和95.2%，进一步证实了基于改进GWO 和标准GWO 的AFMR切面特征提取方法能够适应大动态SNR 的情况，并且也说明了改进GWO 具有更好的抗噪能力。

图8 SNR=0～20 dB 时，3 种方法提取到AFMR 切面特征值的分布Fig.8 Distribution of eigenvalues of AFMR slices extracted by three methods at SNR=0—20 dB

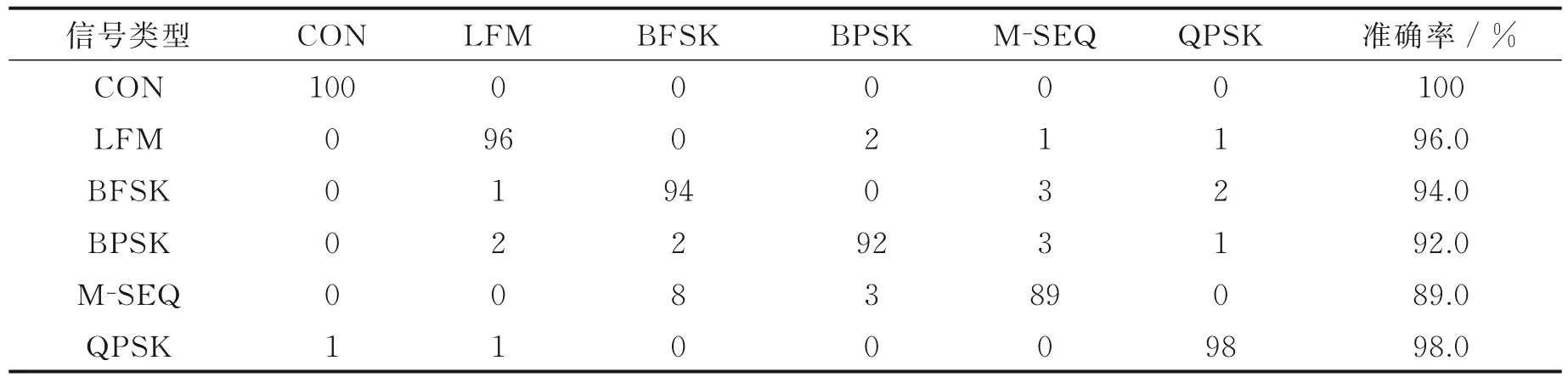
表5 穷举法提取特征值的聚类结果（按行方向）Table 5 Excavation method to extract clustering results of eigenvalues（By row direction）

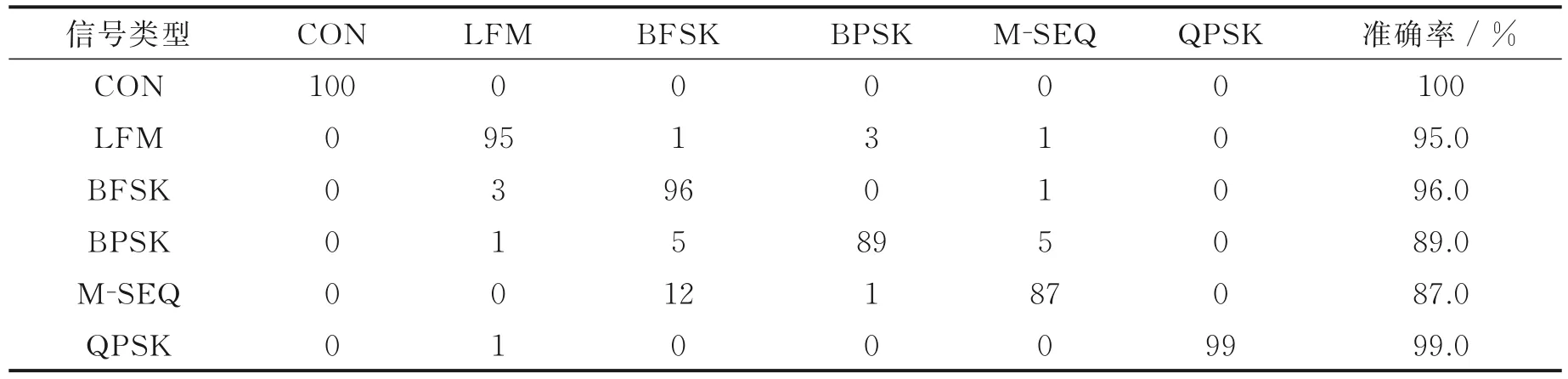
表6 标准GWO 提取特征值的聚类结果（按行方向）Table 6 Standard GWO to extract clustering results of eigenvalues（By row direction）

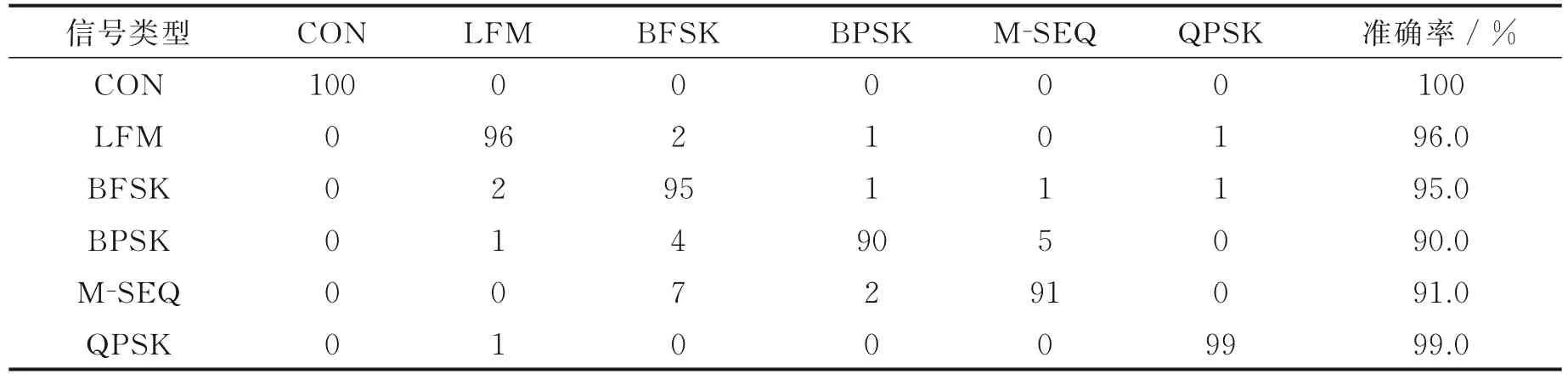
表7 改进GWO 提取特征值的聚类结果（按行方向）Table 7 Improve GWO to extract clustering results of eigenvalues（By row direction）

4 结束语

穷举法需对AF 切面进行1 800 次搜索后筛选出最优解，耗时长且精度低。而改进GWO 方法则通过更新位置参数来逐步逼近最优解，不仅提高了搜索时效性，也保证了解的准确性。实验结果表明，改进GWO 的搜索效率较穷举法和标准GWO 算法分别提高了75.7% 和19.0%，搜索精度有了进一步提高，而且在低SNR 与动态SNR 的情况下均具有较高的搜索准确性与稳健性，表现出了较好的抗噪能力。此优化策略在搜索精度和细微表征方面的提取上有较大提升空间，这将是下一步研究的方向。