基于模式空间算法的声源二维DOA 估计

张 祺，巩朋成，郑毅豪，邓 薇，张正文

（湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉，430068）

引 言

基于麦克风阵列的声源定位是通过多个麦克风接收声音信号，采用适当的估计算法估计声源入射方向角，用以判断声源方向的一项技术。麦克风阵列技术在车载系统、音视频会议、人机交互、助听器、监控系统等方面有着广泛应用[1-7]。基于波达方向估计的麦克风阵列声源定位在许多领域成为了研究的重点，其原理是利用麦克风阵列接收到的声源信号的相位信息，再通过计算进行声源定位，最终得到声源的位置信息。

常见的声源波达估计算法有：基于高分辨率谱估计算法，如多重信号分类(Multiple signal classification，MUSIC)算法，旋转不变子空间(Estimation of signal parameters via rotation invariant technique，ESPRIT)算法；基于可控波束形成算法，如最小方差算法(Minimum variance，MV)算法。其中MUSIC 算法构建信号子空间将声源信号最大化，在噪声抑制、定位精度上，较传统波束形成算法、ESPRIT 算法有着明显的优势。MUSIC 算法最初由Schmidt 等[8]提出，该算法是子空间算法的里程碑，之后以MUSIC 为基础，在声源定位、语音增强等领域迅速推广。Liu 等[9]将MUSIC 算法和ICA 算法进行组合，成功估计出两个非相干声源信号。Wang 等[10]提出了一种新的混合阶MUSIC 算法，其使用稀疏对称阵列进行远场和近场源的定位，虽然估计分辨率提高，但计算量大。

在此基础上，燕学智等[11]设计了一种远近场混合源定位的新方法，其不仅降低了计算复杂度，同时提升了定位精度，且无需参数匹配和二维搜索，但只针对均匀线阵。郑春红等[12]结合非圆信号的特性并加入辅助阵元法，提出一种实值MUSIC 算法，其结合了非圆信号输出阵列实值扩展的特性，减少了算法计算量的同时也提升了阵元输出信号的利用效率。Gao 等[13]在声源数量未知时，提出了一种改进的加权MUSIC 算法来提高多声源的定位性能，在多源环境中也有较高的定位准确度，但算法计算量仍然很大。吴江涛等[14]针对MUSIC 算法在中低频段分辨率下降及聚焦性能差的问题提出基于Group Lasso 改进的MUSIC 算法，增强了MUSIC 算法声源定位的聚焦效果。

针对定位算法在低信噪比条件下精度急剧减小的问题，Liu 等[15]提出了一种四阶累积量(Fourth-order cumulant, FOC)矩阵的重加权稀疏表示框架，用于精确DOA 估计，即使在信噪比（SNR）较低情况下，所提算法成功估计概率也很高。Yang 等[16]提出了应用于四阶累积量矩阵(Fourth-order cumulant matrix, FCM)的广义空间平滑方案，通过平滑的FCM，可以在由四阶MUSIC 算法生成的伪谱上实现相干和独立信号的DOA 估计。郭业才等[17]基于四阶矩提出一种单矢量水听器多声源定位算法，结合四阶矩虚拟扩展的特性，通过提取有效阵元减少冗余，有效降低了计算量，提升了低信噪比下算法计算精度。 Wu 等[18]设计了一种基于四阶累积量改进的稀疏迭代协方差的估计（SPICE）方法，它具备与SPICE 相同的特性，但在低信噪比情况下拥有更高的分辨率和优越性。

为了解决上述MUSIC 算法存在的问题，本文在远场条件下提出一种基于四阶累积量改进的MUSIC 算法，即UCA-I-FOC-MUSIC 算法。与文献[16]和[17]相比，本文有以下不同：（1）针对MUSIC 算法对声源数的限制以及对相干信号估计失准的问题，本文利用模式空间算法对圆形麦克风阵列预先虚拟化线阵处理，同时引入空间平滑技术对相干信号进行解相干，最后加入四阶累积量矩阵重构接收数据，成功估计出多个相干声源信号的DOA。（2）在构建四阶累积量矩阵时，本文通过提取有效阵元信息去掉冗余数据以降低计算量，同时与传统累积矩阵构建相比，本文没有运用克罗内克积构建累积矩阵，因此信号子空间并未被扩张，从而剔除声源DOA 估计时的干扰因素，使得算法的定位性能得到提升。

1 圆形麦克风阵列模型

本文考虑利用圆形麦克风阵列进行二维DOA 估计。假设使用均匀圆形麦克风阵列（UCA）模型，其中M个阵元均匀分布在半径是R的圆周上，且相互独立，其模型如图1 所示。假定存在N个远场声源信号Si(t) 入射到UCA 上，以坐标原点O为参考点，同时以第一个麦克风所在半径作为参考线（图1 虚线），任意声源信号Si(t) 在xoy平面投影是OL，与参考线的夹角是方位角φi，Si(t) 与z轴 的 夹 角 是 俯 仰 角θi，其 中 方 位 角φi∈[0°,360°]，俯 仰 角θi∈[ ]0°,90° ，取逆时针为正方向，则该阵列信号模型可表示成

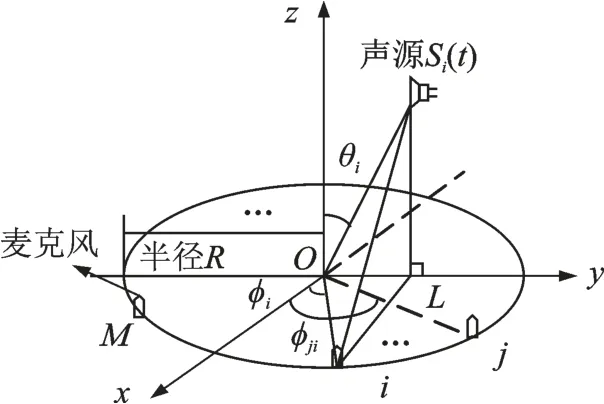
图1 圆形麦克风阵列模型Fig.1 Model of a circular microphone array

将式(1)写成矩阵形式为

式中：X(t) 为M× 1 维的输出数据向量；S(t) 为N× 1 维的远场语音信号；N(t) 为M× 1 维的噪声数据，且为加性高斯白噪声，而每个阵元上的噪声不相关；A=[a1(w0),a2(w0),…,aN(w0) ] 为M×N维阵列流型矩阵，而ai(w0),i= 1,2,…,N为导向矢量，其表达式如下

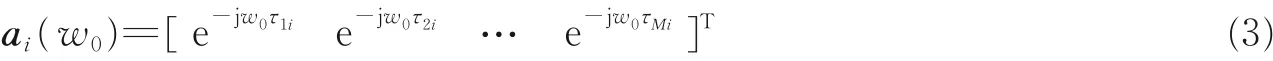
式中：w0为接收信号的角频率，且w0= 2πf0=2πc/λ，c表示声速；τMi表示相对于参考阵元第M个阵元接收到第i个信号的时间延迟。

由图1 可知，第j个麦克风(j=1,2,…,M)方位角为

相比于参考原点，此时信号到达第j个麦克风的传播时延为

于是，式(3)中的导向矢量变换为

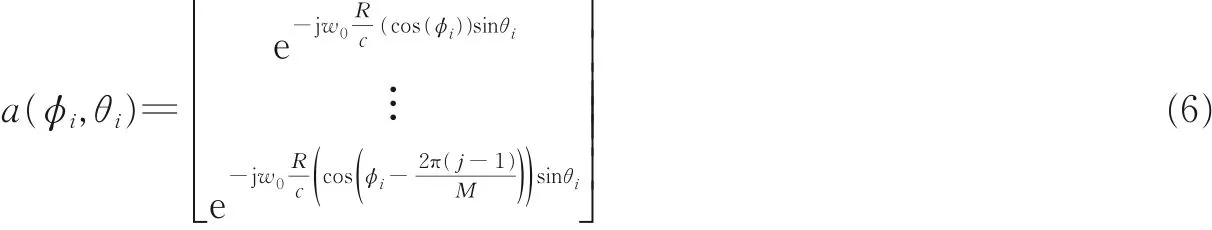
利用式(6)，阵列流型矩阵可定义为

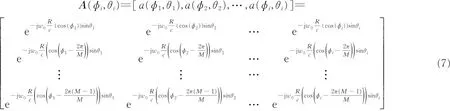
利用式(1)―(7)，N 个独立声源信号入射到M 个均匀圆形麦克风阵，接收数据可转化为

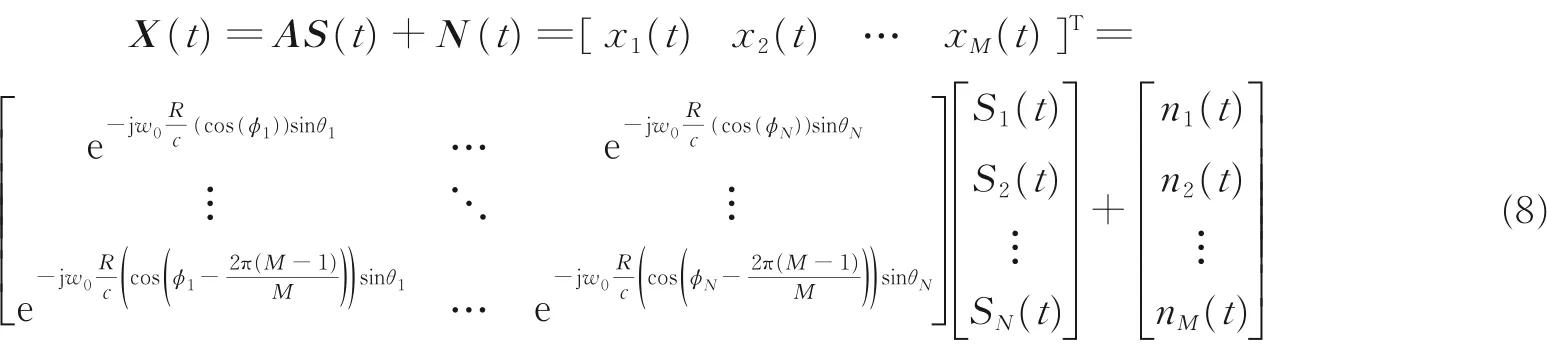
特别地，当声源信号源之间的数学表达式满足一定的规律时，如信号源视为相干信号，则有

因此，均匀圆形麦克风阵列上接收到的N 个相干信号可以视为由S1(t) 生成，而S1(t) 也被称为生成信号源，将式(9)代入式(2)得到均匀圆形麦克风阵列相干信号源的数学模型为

2 UCA-I-FOC-MUSIC 算法

2.1 圆形麦克风阵列中模式空间虚拟线阵算法

该节考虑利用模式空间算法[19]将阵元空间中的UCA 虚拟化成模式空间中的ULA，以模式空间为媒介，实现从UCA 到ULA 的转化。

根据式(2)和式(3)，得到UCA 的第m 个阵元输出为

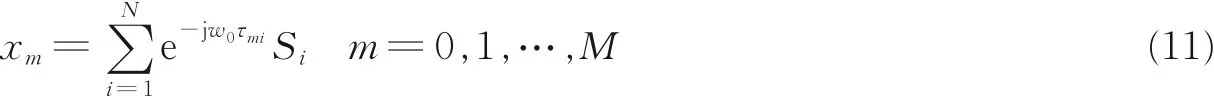
对式(11)进行空间M 点的离散傅里叶变换(Discrete Fourier tansform, DFT)，有

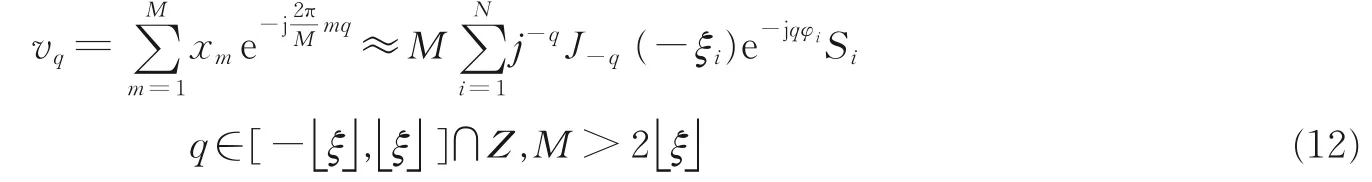
如果令uq= v-q，式(12)改写成矩阵形式为

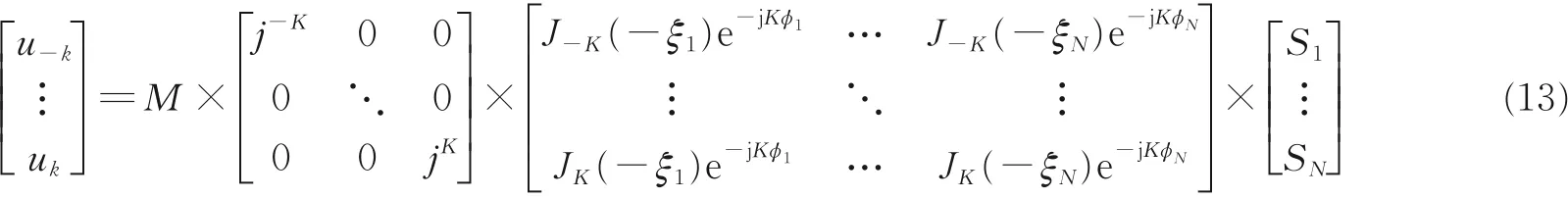
其等价于

于是对于空间DFT，将式(12)可以改写成矩阵形式，即

利用式(13)，(14)和(15)，可得

2.2 UCA-I-FOC-MUSIC 声源估计算法

该节考虑利用四阶累积量以增加有效阵元个数，展宽有效孔径，实现对多个声源信号的DOA 估计。结合文献[20]，得到任意阵列接收信号的四阶累积矩阵

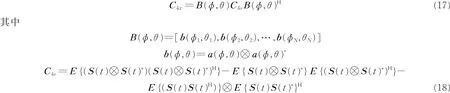
式中：b( φ,θ )为阵列扩展后的导向矢量，C4s为信号S(t)的四阶累积量。

根据以上的推导，采用模式空间变换的方法对式(10)进行阵列预处理，得到

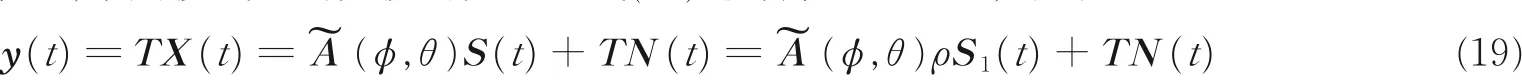
因此，为了估计相干信号，结合文献[21]，本文加入空间平滑技术，其核心思想总结为：采用一定的变换或者相关方法来恢复信号协方差矩阵的秩。而本文基于该思想，通过将划分后得到的子阵接收数据所构建的四阶累量矩阵相加达到类似空间平滑恢复矩阵秩的效果，将平滑处理后的四阶矩阵进行特征值分解，最终达到对相干信号DOA 估计的目的。因此将虚拟线阵划分为L 个子阵，同样数据矢量y (t) 被划分为L 个子矢量，而TN (t) 为线性变换，在处理后噪声被认为是高斯噪声，一般假定信号都是零均值的平稳非高斯过程，在引入四阶累积量处理时，因为噪声信号可以视为零均值的高斯过程，加上四阶累积量对高斯噪声的抑制特性。此时，高斯噪声项的四阶累积量默认是零。所以处理时省略噪声项的分析[22-23]，即将式(19)可改写为

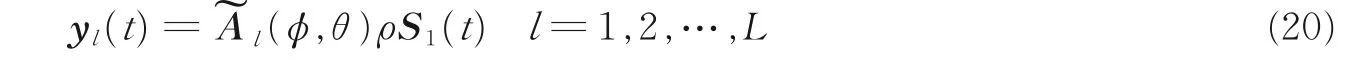
划分子阵后，利用各个子阵的信号接收数据，结合拆分后的第l个子阵的数据yl(t)，重构四阶累积矩阵，最终估计出相干信号的波达方向。利用四阶累积量构建过程，将子阵数据yl(t) 代入式(17)中，四阶累积矩阵可转化为Cl，即

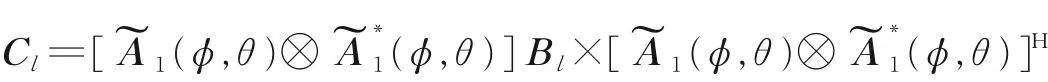
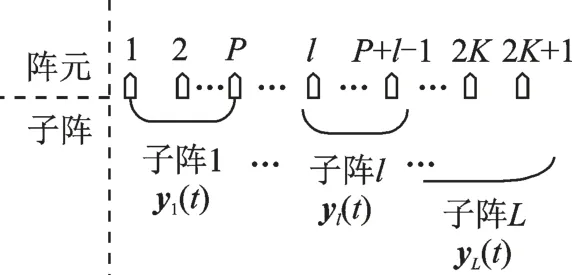
图2 虚拟线性麦克风阵列子阵划分示意图Fig.2 Schematic diagram of sub-array division of virtual linear microphone array

而Cs= cum (S1(t) ,S1∗(t),S1(t),S1∗(t))为S1(t) 的四阶累积量，根据以上的论证，对于所有得到的子阵四阶累积矩阵，其阵列流形相同，同时都是3 个矩阵相乘的形式，因此推广空间平滑技术的思想，令所有子矩阵相加得到常规四阶累积矩阵

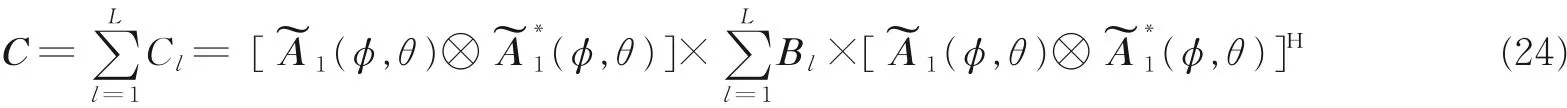
通常情况下，∑Bl秩能恢复为子阵个数L，从而达到恢复矩阵秩的目标，因此在选取时L的值需要比目标信号个数大，同时噪声子空间维数会相应减少几维，但当L取值过大时，除了正确的到达角被估计外，可能会出现不存在的虚假信号到达角被估计的情况，虽然上述常规四阶累积量C可以达到恢复矩阵秩的目的，但在构建过程中信号子空间因为克罗内克积而被扩张，导致算法估计性能降低从而影响计算结果，因此，本文在此基础上构建改进的四阶累积量阶累积矩阵，将其标记为C 'l，即

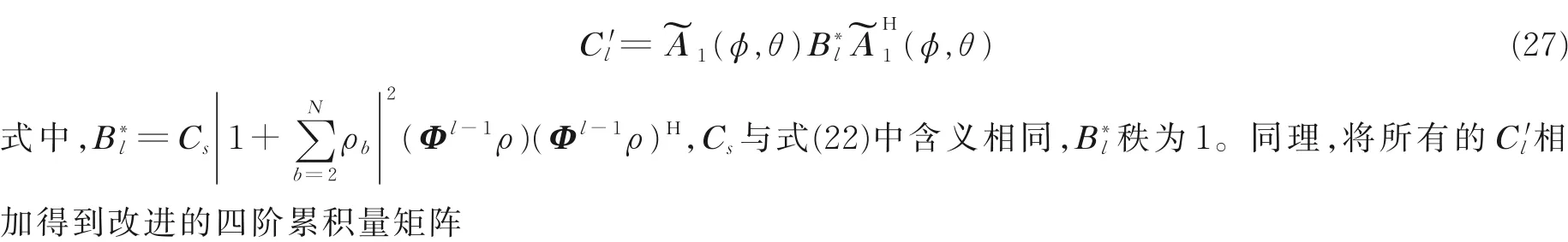
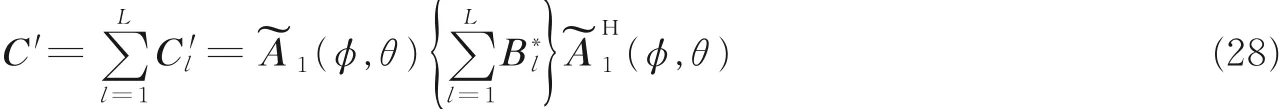
上述所得新的四阶累积量矩阵的秩也为N，其证明过程如下。

首先，等式(25)每个元素可以写成

因此，当L ≥N，此时rank ( ∑B∗l)= N；所以当Q,P ≥N 时，rank (C ') = N，至此证明结束。

相对于构建常规四阶累积量时，信号子空间没有因为克罗内克积而被扩张，因此本文所构建的新的四阶累积量不仅可以恢复矩阵的秩，而且算法的估计性能得到提升，同时减少了计算量。

根据文献[24]，本文所构建新的四阶累积量矩阵符合MUSIC-like 算法使用条件。对构建的四阶累积量矩阵C '进行特征值分解，将得到的P 个特征值按降序λ1＞λ2＞…＞λP排列，信号子空间为ES=( e1,e2,…,eN)，噪声子空间为EN=( eN+1,eN+2,…,eP)，可得空间谱代价函数为

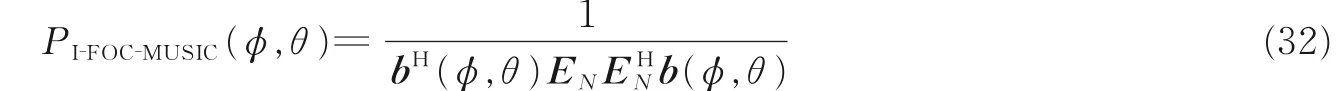
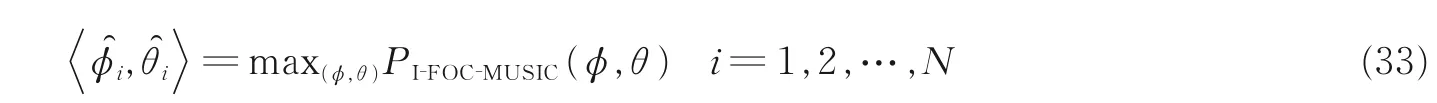
综上所述，本文提出的UCA-I-FOC-MUSIC 算法的具体步骤如下：

（1）基于远场相干声源信号条件下，得到接收数据X(t)；

（2）利用模式空间变换将均匀圆形麦克风阵列虚拟化线阵，得到虚拟线性麦克风阵列的接收数据y(t) 以及新的阵列流型矩阵～A(φ,θ)；

（3）将虚拟线性麦克风阵列拆分，得到L个子阵以及子阵的接收数据yl(t)；

（4）利用所得到的每个子阵接收数据yl(t)，推广空间平滑技术的思想并构建新的四阶累积量矩阵C '；

（5）结合MUSIC-like 算法，对构造的四阶累积矩阵C '进行特征值分解得到相应特征向量，构建空间谱代价函数PI-FOC-MUSIC(φ,θ)，通过谱峰搜索得到声源信号的方位角与俯仰角。

3 仿真分析

3.1 声源信号角度估计

实验1：将本文提出的算法与UCA-RB-MUSIC 算法进行仿真实验对比，选取二维均匀圆形麦克风阵列，将16 个麦克风均匀分布于xoy平面半径为22 cm 的圆周上，噪声为高斯白噪声，远场两个相干声源 信 号 的 方 位 角( 60°,50°) 和( 200°,30°) 入 射 到 该 圆 阵 ，信 号 频 率 分 别 为1 500 和1 000 Hz，快 拍 数 为300，依据第2 节中理论推导，对声源信号参数分析得到ξ= 6.09，则K=ξ= 6，因此圆形麦克风阵列可由模式空间算法转化为13 个阵元的虚拟线阵，结合本文算法的推导，选取L=10，P=4 进行DOA 估计，而SNR 分别选取-5 和20 dB 两种情况，取φ和θ的搜索步长为1°，φ的搜索范围为[ 0°,360° ]，θ的搜索范围为[ 0°,90° ]。仿真结果分别如图3，4 所示。

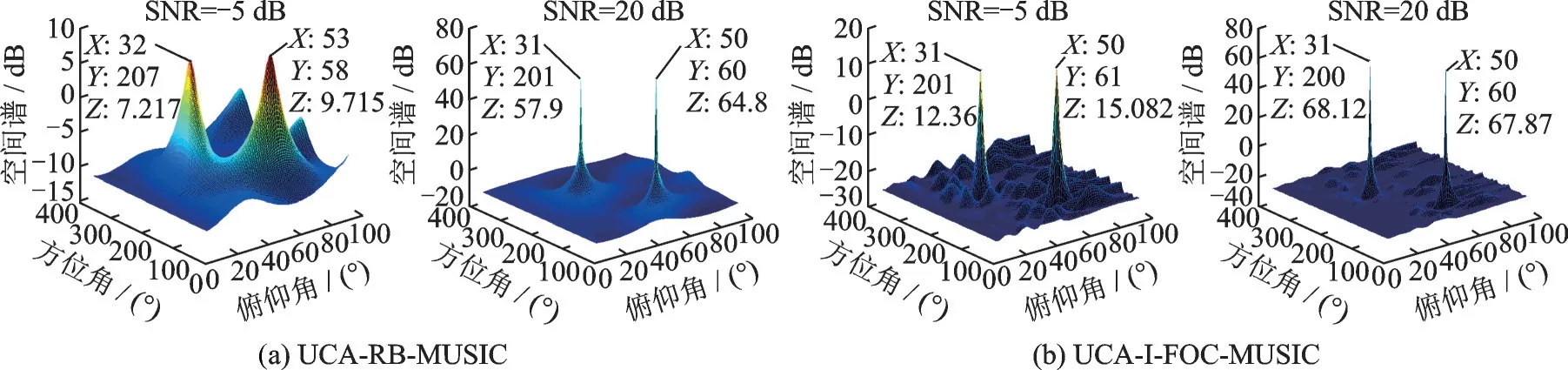
图3 两种算法的三维定位空间谱图Fig.3 Three-dimensional positioning spatial spectrum of the two algorithms

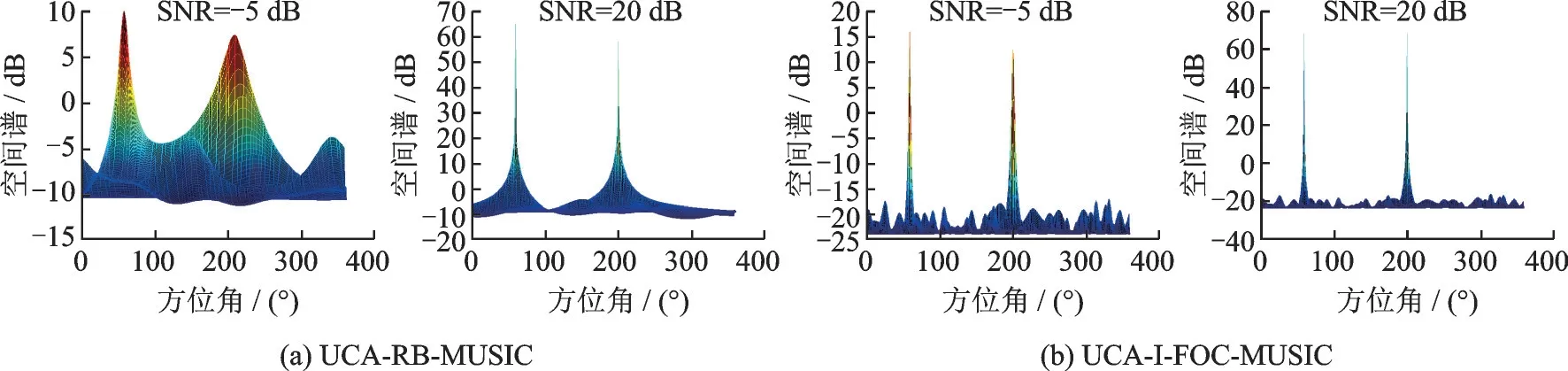
图4 两种算法空间谱在方位角上的投影Fig.4 The projection of the spatial spectrum of the two algorithms on the azimuth angle

通过图3 和图4 可知，相比于经典UCA-RB-MUSIC 算法，本文提出的算法即使在低信噪比时也有较高的角度分辨率，方位角最大提升了6°，俯仰角最大提升了3°，并且在不同SNR 下所得到的空间谱孔径大小没有明显变化且都集中于一点。并且在低信噪比时，UCA-RB-MUSIC 算法得到的空间谱孔径较大，并随着SNR 变化而发生明显变化；同时在不同SNR 情况下本文算法所得到的方位角投影上空间谱的谱峰更加尖锐。因此证明了本文算法在总体估计性能上优于经典UCA-RB-MUSIC 三维声源定位算法。

实验2：在多个目标条件下，验证本文提出的算法。设定SNR 为20 dB，选取远场8 个方位角分别为( 60°,50°)，(120°,40°)，(120°,60°)，(160°,30°)，(160°,70°)，( 200°,40°)，( 200°,60°) 和( 230°,50°) 的相干声源信号，信号频率分别为800、900、1 000、1 100、1 200、1 300、1 400 和1 500 Hz，其他实验条件与仿真实验1条件一致，仿真结果如图5 所示。

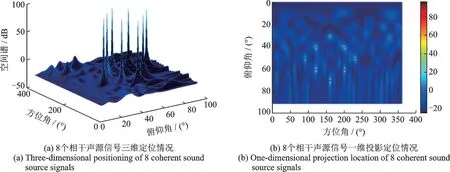
图5 UCA-I-FOC-MUSIC 对8 个相干声源信号估计情况Fig.5 UCA-I-FOC-MUSIC's estimation of 8 coherent sound source signals

由图5 可知，本文算法在高信噪比情况下可以实现对多个相干声源信号的估计，并且在高信噪比情况下角度分辨率依然比较高。

3.2 声源定位精度分析

为了进一步考察算法的定位性能，本文仿真UCA-FOC-MUSIC 算法，UCA-ESPRIT 算法，UCARB-MUSIC 算法以及UCA-I-FOC-MUSIC 算法的DOA 估计性能与声源信号信噪比之间的性能曲线图，计算每个算法定位所需时间以及成功率，而DOA 估计性能一般用均方根误差(RMSE)来进行比较，本文中涉及二维测量，因此均方根误差包括方位角误差和俯仰角误差两部分。

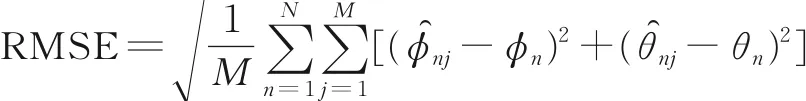
其中：M表示进行蒙特卡罗仿真实验的次数，分别表示第j次仿真实验得到的第n个声源信号的俯仰角和方位角的估计值，θn和φn即分别为真实的俯仰角和方位角的值。

实验3：设置SNR 在20 和-5 dB 的情况下，其他条件与上述仿真实验1 条件相同，蒙特卡罗仿真实验次数为300，计算各个算法声源方位估计时间。 测量时使用MATLAB 2014a 版本分析运行时间（表1），在标准PC 上运行(配备Intel 2.6 GHz 核心i5 CPU 和4 GB RAM)。

从表1 中得出，UCA-ESPRIT 算法声源定位耗时最短，用时最长的是UCA-FOC-MUSIC 算法，但UCA-ESPRIT 和UCA-RB-MUSIC 算法在低信噪比和多声源定位时会遇到困难，而本文算法在同样的情况下，所需要的估计时间更少。

表1 算法运行时间比较Table 1 Comparison of algorithm running time

实验4：设置快拍数为300，同时设定估计值与真实值的偏差小于1°的成功概率，SNR 的设定范围为[-5, 20] dB,其他条件与上述仿真实验3 条件相同，共进行300 次蒙特卡罗仿真实验，图6 比较了不同算法的估计成功率和均方误差。

由图6(a)可知，本文算法的成功率优于其他3 种算法，在SNR 为-5 dB 时成功率接近80%，而其他算法均未超过70%，直到SNR 大于10 dB 时，4 种算法成功率几乎都为100%，同时由图6(b)的均方根误差结果看出，在低信噪比情况下UCA-ESPRIT 算法、UCA-RB-MUSIC 算法有着较大的误差，但在高信噪比情况下，这4 种算法都拥有较好的估计性能。对比其他3 种算法，本文算法更能实现对相干信号DOA 的高精度估计。

实验5：考虑不同子阵数L和子阵阵元数P对本文算法估计精度的影响，对其进行仿真实验，阵列参数和声源信号参数与实验3 相同，当使用全部子阵时，L和P满足关系：P=2K+2-L，设置P的变化范围为[1∶1∶13]，蒙特卡罗仿真实验次数为300。仿真结果如图7 所示。

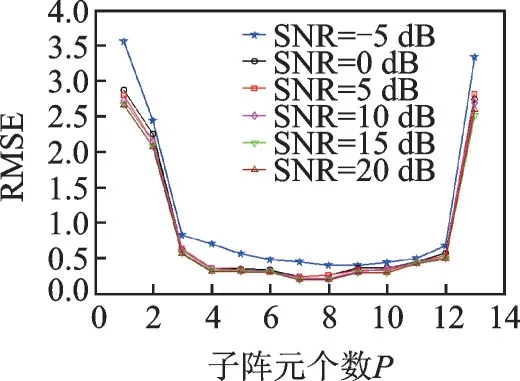
图7 全部子阵使用时，算法随子阵阵元数P 变化时的性能曲线Fig.7 Performance curve of the algorithm when all sub-arrays are used with the number of sub-array elements P

由图7 可知，当子阵阵元数P增加时，本文算法的RMSE 的值先降低后升高，这说明子阵阵元数P的设定不要太小，一般要大于声源信号的个数，不然误差太大会导致算法无效。同时P也不能设置太大，否则使用空间平滑的子阵个数太少，算法估计精度下降，造成曲线后半段有上升的趋势。但是当合理挑选P的值后，在使用全部子阵的情况下，不同的P值对DOA 估计的精确度没有太大改变，特别是信噪比高于-5 dB 后，当信噪比逐渐增加时，曲线几乎重叠为一条。因此，为了进一步考察P和L对于算法估计性能的影响，当使用部分子阵时，同样进行仿真实验。设置信噪比逐级递增，其余参数维持一致，进行300 次蒙特卡罗仿真实验。首先维持P不变，让L逐渐增加。图8 是6 种不同子阵个数条件下算法角度估计精度的RMSE 与SNR 的关系变化图，设定子阵阵元P为4，而L＜2K+2-P，即L值由4递增到9。

由图8 可知，当子阵个数L和信噪比逐渐增加时，算法角度估计RMSE 随之下降，尤其是低信噪比时，RMSE 的减小趋势更加明显，但当信噪比逐渐提高时，减小的趋势减缓，慢慢趋于统一，因此，当子阵阵元个数一定时，随着子阵个数增加，算法估计性能得到提升，尤其在低信噪比、子阵个数少的条件下。但当信噪比和子阵个数慢慢增加时，这种趋势开始减缓，并逐渐趋于稳定。接着，当维持L不变时，让P逐渐增加。图9 是6 种不同子阵阵元数值条件下算法角度估计RMSE 与SNR 的关系变化图，但此时设定子阵个数L为6，而P值由1 增加到6。

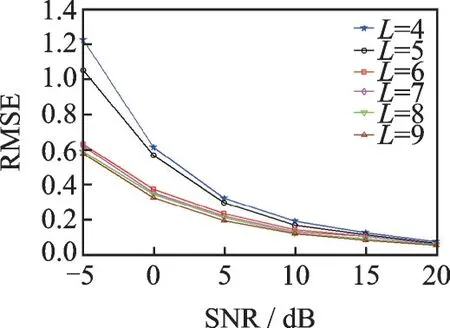
图8 算法DOA 估计的RMSE 与子阵数的关系Fig.8 Relationship between RMSE estimated by algorithm DOA and the number of sub-arrays

图9 算法DOA 估计的RMSE 与子阵阵元数的关系Fig.9 Relationship between the RMSE estimated by the algorithm DOA and the number of sub-array elements

由图9 可知，当子阵阵元个数P和信噪比慢慢增加时，算法的角度估计RMSE 值随之减小，在低信噪比时，RMSE 的降幅更加明显，但当信噪比增加时，减小幅度开始减缓，慢慢趋于统一。因此，当子阵个数一定，子阵阵元个数增加时，算法估计性能得到提升，尤其在低信噪比、子阵阵元个数少的情况下。但信噪比和子阵个数逐渐增加时，这种提升开始减缓，并最终趋于稳定。

4 结束语

本文研究了一种基于改进四阶累积量矩阵的圆形麦克风阵列声源定位算法。该算法利用模式空间算法将圆形麦克风阵列虚拟化线阵，并推广空间平滑技术构建新的四阶累积矩阵。通过减少阵列重复信息带来的运算量，与构建常规的四阶累积量相比较，信号子空间没有因为克罗内克积的原因被扩张，因此算法的估计性能得到提升，同时降低了计算量并提高了运算效率。最后利用MUSIC-like 算法搜索谱峰得到声源信号DOA 估计值。仿真实验结果表明，该算法结合圆形麦克风阵列实现了对多个相干声源信号的DOA 估计。相比于经典的高分辨率谱估计算法，即使在低信噪比的情况下得到的声源信号DOA 估计值准确度依然很高。