基于QMU原理的离子推力器产品性能设计及验证方法
2020-10-23张雪儿张天平李得天
张雪儿,张天平,李得天
(1.兰州空间技术物理研究所,真空技术与物理重点实验室,甘肃 兰州 730000; 2.甘肃省空间电推进技术重点实验室,甘肃 兰州 730000)
0 引言
离子电推进是当前航天工程应用的主要电推进类型之一[1-4]。由于离子推力器工作的物理过程复杂、各组件之间耦合性强、设计参数众多[5],使得推力器输出性能与设计参数之间缺乏单一、直接和简单的对应关系,再加上工程应用的离子推力器产品性能是对任务需求、工作可靠性和寿命等因素综合考虑的折中结果,这不仅导致离子推力器工程产品研制的周期长、成本高[6-7],而且缺乏统一或公认的产品研制规范[8-9],制约了不同供应商产品之间的通用性。
针对国家核武器库评价和决策需求,由美国国家安全实验室开发的裕度和不确定度量化(QMU)方法[10-12],已经在复杂耦合和缺乏试验数据的工程系统中获得成功应用[13-15],近年来也逐步开始应用于电推进产品及系统[16-17]。基于QMU方法的基本原理,本文提出了一种离子电推进工程产品的性能设计及验证方法,以期能够在离子推力器原理样机研制基础上,提高工程产品研制的设计开发效率和验证评价充分性。
1 离子推力器性能及其设计参数的一般表示
从航天器工程应用的需求出发,离子推力器产品的性能参数用矩阵
P=[F,Isp,ηt,θ,Nc,ts,tm,Nm]
(1)
式中:F为推力;Isp为比冲;ηt为总效率;θ为束流发散角;Nc为开关机次数;ts为启动时间;tm为单次最长工作时间;Nm为工作模式数。离子推力器性能相关的设计参数主要有几何(尺寸)参数、电参数、磁场参数、流率参数和材料特性参数等5个方面。推力器的几何参数用矩阵
G=[Dd,Ld,Dk,Dg,Lg,Hg,Ng,Ds,Da,Ln]
式中:Dd为放电室直径;Ld为放电室长度;Dk为阴极触持孔径;Dg为栅极直径;Lg为栅极间距;Hg为栅极拱高;Ng为栅极开孔数;Ds为屏栅孔径;Da为加速栅孔径;Ln为中和器与束流引出面距离。
推力器的电参数用矩阵
E=[Id,Vd,Ib,Vb,Ia,Va,Ikc,Vkc,Ic,Ihc,Vhc,Ikn,Vkn,In,Ihn,Vhn,Vi]
式中:Id为放电电流;Vd为放电电压;Ib为束电流;Vb为束电压;Va为加速电压;Ia为加速电流;Ikc为阴极触持电流;Vkc为阴极触持电压;Ic为阴极发射电流;Ihc为阴极加热电流;Vhc为阴极加热电压;Ikn为中和器触持电流;Vkn为中和器触持电压;In为中和器发射电流;Ihn为中和器加热电流;Vhn为中和器加热电压;Vi为空心阴极点火电压。
推力器的磁参数用矩阵
B=[B,B]
式中B为放电室磁感应强度,B为磁场分布(梯度),均为放电室空间坐标的函数。推力器的流率参数用矩阵
Q=[Qd,Qc,Qn]
式中:Qd为放电流率;Qc为阴极流率;Qn为中和器流率。推力器的材料特性参数用矩阵
M=[Rc,Rn,Γe,Ee,Ea,Yi,Δb,Gb,Tm,Tc,Ωb]
式中:Rc为阴极加热丝电阻;Rn为中和器加热丝电阻;Γe为二次电子发射系数;Ee、Ea分别为热发射系数和吸收系数;Yi为离子溅射产额;Δb为强度;Gb为刚度;Tm为熔点;Tc为永磁材料居里温度;Ωb为绝缘强度。从工作原理和设计原理来说,推力器的性能参数决定于推力器的设计参数,也就是性能参数为设计参数的函数,不失一般性地可表达为
P=f(G,E,B,Q,M)
(2)
显然式(2)的函数不可能具有解析表达,往往需要基于推力器性能物理模型及相关参数敏感度分析对其进行适当简化,如本文后面讨论中所做。
2 基于原理样机的推力器产品性能分析
设离子推力器已完成原理样机研制,为简化讨论仅考虑推力器为单模式工作,且不涉及推力器的环境可靠性,在此基础上就可以简化式(2)的函数关系。
原理样机设计状态下,推力器的几何参数中绝大部分为确定不变值,随工作过程及时间变化的参数只有阴极触持孔径Dk、栅孔径Ds和Da。只要永久磁体最高工作温度远低于居里温度,磁参数均为不变值。由于相对不敏感,除了加热丝电阻Rc和Rn随工作时间变化外,其他推力器材料特性都可以近似为常数。电参数要复杂些,可分为两类:一类是Id、Vb、Va、Ikc、Ikn、Ihc、Ihn等由电源供应输出特性决定的参数,它们是真正意义上的推力器输入电参数,其中Ikc和Ikn对推力器性能不敏感;另一类是Vd、Ib、Ia、Vkc、Ic、Vkn、In等由推力器工作响应给出的参数,它们具有双重意义,其初始额定值与推力器性能密切相关,其工作时间变化反映了推力器及相关组件的性能退化,其中Vkn和In对推力器性能不敏感。
基于以上分析,式(2)可以简化为
P1=f(G1,E1,Q,M1)
(3)
式中下标1代表原理样机下的一次近似。注意到式(3)中已经没有了磁场参数,且几何参数、电参数和材料特性参数变量都已经发生较大变化,具体为
G1=[Dk,Lg,Ds,Da]
E1=[Id,Vd,Ib,Vb,Ia,Va,Vkc,Ihc,Ic,Ihn,Vi]
M1=[Rc,Rn]
下面分别讨论矩阵P中的每个性能参数,以期获得基于原理样机基础和设计参数及敏感度的近似表达式。
2.1 束流发散角
离子推力器束流发散角主要取决于放电室磁场参数和栅极几何参数中的Lg,Hg,敏感度分析表明与Vd弱相关,由此得到近似表达式为
θ≈fθ(Lg,Hg,B,B)
(4)
关系式中相关参数均不随工作时间改变,可以近似为恒定值,推力器长寿命试验也已证明[18]。如LIPS系列离子推力器的束流发散角典型值为15°。
2.2 开关机次数
开关机次数主要决定于阴极和中和器点火启动次数,由阴极和中和器加热器工作寿命决定,而加热器工作寿命决定于加热电流和加热丝电阻,由此得到近似表达式为
Nc≈fNc(Ihc,Rc,Ihn,Rn)
目前的空心阴极设计能够以足够安全裕度保证推力器具有上万次的点火启动次数。
2.3 启动时间
推力器启动时间由中和器启动时间、阴极及放电室启动时间、束流引出时间的总和决定。束流引出时间取决于栅极加电程序,设定后为固定值。阴极及放电室启动时间几乎等同于阴极启动时间,中和器和阴极启动时间均取决于流率、点火电压、加热电流、加热丝电阻等,与触持极孔径为弱相关。由此得到近似表达式为
ts≈fts(Vi,Qc,Ihc,Rc,Qn,Ihn,Rn)
2.4 单次最长工作时间
对离子推力器而言,单次最长工作时间几乎不受限制,也就是说与设计参数没有关系。在一定程度上受推力器工作可靠性影响,例如发生由于非预期电击穿导致放电熄灭。
2.5 工作模式数
基于本文离子推力器单模式工作假设,工作模式数取1。
2.6 推力
离子推力器推力大小的经典表达式为
(5)
式中:e为电子电荷量;m为推进剂原子质量;α为与束流发散角直接相关的束流发散修正因子;β为与放电电压关系密切的二次电荷离子修正因子。由此式(5)可重写为
(6)
2.7 比冲
推力器比冲经典定义为
式中g0为重力加速度常数。把式(6)代入即可得到比冲性能

(7)
2.8 总效率
离子推力器总效率
(8)
式中Pt为推力器全部电源输入电功率之和。由于阴极和中和器的加热电源功率、点火电源功率都在推力器正常工作之前,其功率不占总功率份额。阴极和中和器触持电源功率、加速电源功率都相对较小可不计。由此可见推力器输入功率主要为束电源功率和放电电源功率之和,并把式(6)和式(7)代入式(8),由此得到推力器总效率表达式为
ηt≈fηt(Ib,Vb,Id,Vd,θ,Qd,Qc,Qn)
3 基于QMU的离子推力器产品性能设计和验证
3.1 QMU基本原理
QMU的基本原理为[11-12]:一个工程系统的应用需求可以用一组性能参数P{Pi}表征,由于影响性能参数的各元素Xj本身具有不确定度Uj,使得工程系统实际获得的性能Pi具有相应的不确定度Ui,为了保证工程系统能够充分可靠地满足应用需求,工程系统设计应当具有足够的性能裕度M{Mi},并且每个性能满足其裕度Mi大于其不确定度Ui的准则,即Mi/Ui>1。
由此可见,基于QMU基本原理完成离子推力器产品设计需要完成如下步骤:
1)根据工程应用需求,确定推力器产品的性能表征集合P{Pi}及每个性能元素Pi的额定要求值或范围;
2)确定(建立)每个性能元素Pi与设计参数及相关变量Xj之间的函数关系(物理模型);
3)分析确定每个设计参数及相关变量Xj的不确定度;
4)应用函数关系(物理模型)分析计算由变量不确定度导致的性能元素Pi的不确定度Ui;
5)进行推力器性能元素Pi的裕度Mi确认,判读是否满足Mi/Ui>1;
6)如果未满足Mi/Ui>1准则,则需要调整相关变量参数或缩小相关变量不确定度,重复以上过程,直到每个Pi都满足Mi/Ui>1,由此确定推力器产品的性能设计状态。
3.2 原理样机
离子推力器产品以兰州物理研究所正在开发的LIPS-200E为例[19-20],LIPS-200E为LIPS-200产品的性能提升与扩展型,原理样机实现的基础性能数据为:推力60 mN,比冲3 500 s,输入功率1 600 W,总效率64%,束流发散角15°,启动时间6 min,开关机不少于10 000次,单次最长工作时间24 h,单一工作模式。除了开关机次数是空心阴极单独验证外,其他性能指标都是推力器原理样机上验证的。
通过第2章中对性能指标的分析可见,由于束流发散角(常数)完全继承原理样机、单次最长工作时间归为可靠性并且工作模式数完全确定,相对式(1)中全部8项性能指标,工程产品上共有5项性能参数需要再设计,表征矩阵为
P2={pi}={F,Isp,ηt,ts,Nc}
(9)
限于篇幅,后面仅针对式(9)所述5项性能中最具代表性的比冲进行基于QMU原理的工程产品设计及验证,并简述推力性能情况,其他3项性能设计的基本方法完全类似。
3.3 比冲性能的设计分析与验证
3.3.1 比冲额定需求
根据LIPS-200E产品应用需求分析和LIPS-200产品研制经验,LIPS-200E产品的比冲性能额定指标(单位为s)为
Isp-0=(3 500±100)
或者用区间表达为
Isp-0=[3 400,3 600]
(10)
3.3.2 比冲及变量物理模型
比冲及其变量的物理模型为式(7),其中包含了Ib、Vb、Vd、Qd、Qc、Qn、θ等7个变量,其中θ作为独立变量处理是基于对式(4)关系的简化,即可以认为θ的不确定度基于式(4)的分析计算。β的额定值取0.967。
3.3.3 各变量不确定度
各变量不确定度应当覆盖推力器全寿命工作期间各变量的变化范围,7个变量中,Vb、Qd、Qc、Qn为束电源和流率供应单元输出特性决定的离子推力器输入量,其不确定度直接由束电源和流率供应单元控制精度决定,对LIPS-200E取值如表1所列。θ,Ib,Vd实际为推力器响应参数,不仅难以直接获取,而且在工作寿命期间的变化趋势是单向递增或递减的,获得这类变量不确定度的主要方法包括专项测试、经验数据和基于模型的数值计算等,这里不准备展开介绍。表1中所列θ、Ib、Vd的不确定度分别来自经验数据(θ和Vd)和模型计算(Ib)。

表1 各变量的额定值及不确定度Tab.1 Ratings and uncertainties of parameters
3.3.4 比冲的不确定度计算
基于式(7)的比冲不确定度传递关系
(11)
其中具体各变量参数为
X1=Ib,X2=Vb,X3=Vd,X4=Qd,X5=Qc,
X6=Qn,X7=θ
(12)
经过具体推导和计算,得到表2所列的具体值,其中与Vd相关的β(Vd)的偏导数计算基于放电电压与双荷离子电流的测量结果,以及据此得到的放电电压与双荷离子比例的经验关系。
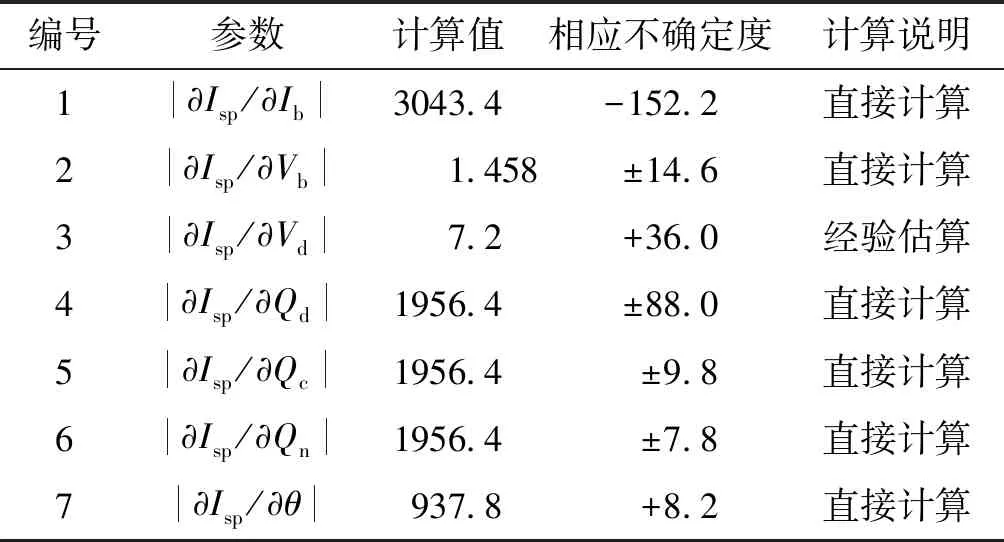
表2 比冲性能参数不确定度计算的相关量值Tab.2 Values for uncertainty computation of specific impulse
表2中数据代入式(11),得到比冲在3 500 s中心值的不确定度量值为
δIsp=3 500=+12.2 -228.2
(13)
再把式(13)中数据应用到额定比冲区间式(10)的上下边界处,分别得到考虑不确定度后的比冲上下边界变化范围
Isp=3 400=[3 171.8,3 412.2]
Isp=3 600=[3 371.8,3 612.2]
由此可见,变量参数不确定引起的比冲不确定,使得考虑不确定度后的比冲参数范围扩展到
Isp-U=[3 171.8,3 612.2]
(14)
或者用不确定度表示为
UIsp={228.2,12.2}
(15)
3.3.5 比冲裕度
裕度定义为系统实际具有(获得)的性能与额定性能之差值,对额定性能参数为区间的比冲,如果定义实际推力器获得的比冲范围
Isp3=[Isp-min,Isp-max]
则比冲裕度表示可定义为
MIsp={3 400-Isp-min,Isp-max-3 600}
(16)
3.3.6 比冲性能验证
在LIPS-200E离子推力器工程样机上进行了实际性能测试,针对比冲的性能测试方法为:推力器的流率、磁场和除放电电流以外的电参数都取设计额定值,分别减小和增大调节放电电流,并以总功率不超过1 600 W、放电电压不超过37 V、束流变化不超过±0.03 A为约束条件,测量获得的实际比冲最大值为3 765 s、最小值为3 118 s,该结果代入式(16)得到推力器工程产品比冲裕度为
MIsp={282,165}
(17)
对比式(17)和式(15)结果可见,在额定比冲上下边界处,比冲裕度和不确定度比值分别为13.5和1.2,均满足大于1的判据条件。
3.4 其他性能设计分析与验证
前面3.3节中针对比冲性能的分析验证结果,可以用图更直观地体现QMU的思想和结果对应关系。如图1所示,比冲额定值区间[3 400,3 600]为最小区间,考虑不确定度后的比冲区间变为[3 171.8,3 612.2]且双向扩展,比冲裕度区间决定于产品设计和制造,应具有最宽范围[3 118,3 765]。从产品实际性能应满足要求的角度看,裕度区间仅覆盖额定区间还不够,只有裕度区间完全覆盖不确定度区间时,才能可靠保证产品实际工作性能满足工程应用需求。
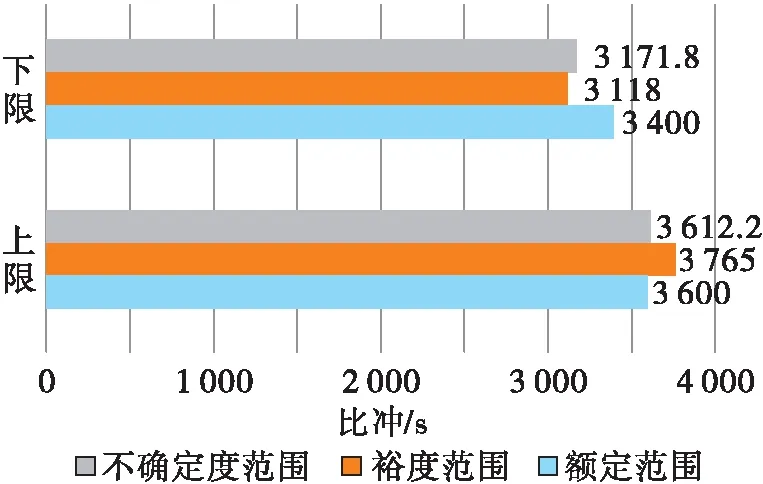
图1 比冲额定区间、裕度区间和不确定度区间的关系Fig.1 Intervals of rating, margin and uncertainty of specific impulse
LIPS-200E其他性能设计分析和验证与比冲性能类似,这里仅以推力性能为例给出简要结果而略去具体过程。
推力额定区间为[58,62],单位为mN。推力相关变量物理模型为式(6),各变量不确定度取表1中数据,类似式(11)比冲不确定度计算过程,得到推力不确定度相关计算如表3所示。

表3 推力性能参数不确定度计算的相关量值Tab.3 Values for uncertainty computation of thrust
由此得到推力不确定度为
UF={2.3,-1.8}
(18)
推力裕度通过测试试验获得,测试条件与比冲测量一致,具体结果为
MF={2.5,0.6}
(19)
比较式(19)和式(18)可见,产品推力性能也满足裕度大于不确定度的要求。注意到在推力额定性能上边界上,不确定度为负值,其物理意义在于随推力器工作时间不断累计,变量参数引起的推力总体上是向逐渐减小方向发展,这也符合推力器寿命试验中获得的变化趋势。
4 结语
本文提出了一种基于原理样机研制的离子推力器工程产品的性能设计及验证方法,该方法应用QMU的基本原理,通过产品性能表征、性能与其相关变量物理模型建立、相关变量不确定度确定、性能不确定度计算、性能裕度测试、性能裕度完全覆盖不确定确认等步骤及方法,可以确保产品的实际性能完全满足工程应用需求。
基于QMU原理的离子推力器产品性能设计及验证方法考虑了推力器性能相关因素(变量参数)自身存在的不确定度影响,包括输入控制变量的随机不确定度和产品响应变量的衰退变化不确定度,只要确认产品实际性能具有足够裕度:性能裕度大于性能不确定度,就可以保证研制产品能够完全满足工程实际应用需求。由此该基本方法可做为离子推力器工程产品研制的规范去应用并推广。
以LIPS-200E离子推力器产品为实例,在分析计算过程中进行了适当简化,包括应用了经验关系及数据;但并不影响方法的通用性和可行性,因为在比较成熟的QMU框架中,对限于知识、经验、数据等严重不足的变量及性能,已有分析计算不确定度量的通用方法,可据此进一步提高分析精度。
