智能低压电网网络分段时延测量技术研究
2020-10-22洪海敏冷安辉贺竞辉何先灯梁昌鹄罗冬坤
洪海敏 冷安辉 贺竞辉 何先灯 梁昌鹄 罗冬坤


摘 要: 对智能低压电网终端、分支点、集中器之间分段时延测量的研究,有助于其网络拓扑的发展。为解决现有测量技术,不能高精度在线测量端到端、端到分支点之间时延的问题,该文提出一种基于电力线通信技术和扩频通信技术相结合的低成本、高精度时延测量技术,通过仿真研究并给出了该系统抗白噪声、多径以及窄带干扰的性能指标。仿真结果表明,所提技术,在信噪比大于-11 dB的白噪声、信干比大于4 dB的多径信号以及信干比大于-3 dB的窄带干扰下,均能实现±10 ns的测量精度。
关键词: 低压电网; 网络分段; 时延测量; 电力线通信; 抗干扰; 仿真分析
中图分类号: TN913.6?34; TP914.42 文献标识码: A 文章编号: 1004?373X(2020)20?0179?04
Research on measurement technology of network sectional delay in smart low?voltage grid
HONG Haimin1, LENG Anhui1, HE Jinghui1, HE Xiandeng2, LIANG Changhu1, LUO Dongkun1
(1. Shenzhen Guodian Technology Communication Co., Ltd., Shenzhen 518109, China; 2. Xidian University, Xian 710071, China)
Abstract: The research on the measurement of sectional delay between terminals, branches and concentrators of smart low voltage grid is helpful to the development of its network topology. A low?cost and high?precision delay measurement technology based on the combination of power line communication technology and spread spectrum communication technology is proposed to solve the problem that the existing measurement technology can not accurately measure the delay between end?to?end and end?to?branch points online. The performance indexes under anti?interference of white noise, multi?path signal and narrowband signal are given by means of the simulation research. The simulation results show that the proposed technique can achieve ±10 ns measurement accuracy under the white noise with signal?to?noise ratio greater than -11 dB, multi?path signal with signal?to?interference ratio (SIR) greater than 4 dB and narrowband interference with SIR greater than -3 dB.
Keywords: low voltage grid; network section; delay measurement; power line communication; anti?interference; simulation analysis
0 引 言
低压电网[1]是智能电网[2?4]的重要构成部分,它一般指380 V/220 V的电压等级的电力配送网络。一个典型的低压电网由台区变压器、传输线、线路分支(通常安装分支开关)、用户电表构成。智能低压电网,通常在台区变压器处安装集中器,在部分分支开关和用户电表处安装采集器。采集器和集中器利用电力线通信模块,完成低压电网通信网络的建立,并监控用户的用电信息[5]。
目前建立的低压电网主要依赖电力网络,由录入到系统中各个分支开关和用户电表的信息构成。由于面临着安装错误和表计更替等问题[6],造成实际运行的物理拓扑与规划设计时的不一致。为解决越来越复杂的低压电网拓扑结构和电网公司对低压电网的管理越来越精益化的需求,对低压电网物理拓扑发展的研究变得更为重要[7]。
文献[8?9]分别提出了一种基于工频信息采集的台区识别和象限识别方法,文献[7,10]通过机器学习和数据挖掘技术,对大量采集的用电信息进行分析,更准确地识别出了台区、象限以及集中器和采集器的从属关系,但文献[8?10]均无法判定该台区内电表之间的物理拓扑关系,如哪些电表在同一个表箱或同一条分支线路等。
由于低压电网的物理拓扑是一种树状拓扑结构[1,11?12],其典型单元为T型网络分支,如图1所示。其中A,B,C为用户电表或者下一级分支开关,D为分支点。通过测量AD,DC和DB的传播时延t1,t2和t3 (ns级精度),可得到三者相对位置关系,再利用网络层析技术,最终可以获得准确的低压电网的物理拓扑[13?14]。
本文提出一种利用电力线通信模块和扩频通信技术,在低压电网中实现高精度端到端的传输时延测量技术,并利用该技术计算,给出终端、分支点、集中器之间分段时延,从而为低压电网物理拓扑发展提供了重要的参考数据。
1 端到端传输时延测量技术研究
现有的传输时延测量技术,主要有3类。
1) 基于通信的端到端网络传输时延测试技术,常见于计算机网络通信端到端传输时延测试[14]和无线通信网络端到端传输时延测试。通过记录收发网络时延探测包(比如Ping命令)的时间差,得到端到端传输时延。受限于通信的传输速率及物理层传输控制机制,该时延测量精度通常都在μs级以上[9,15],不能满足T型分支结构时延测量ns级分辨率的要求。
2) 基于脉冲法的传输时延测量技术,主要应用于网线、电缆、光纤长度测试以及UWB定位系统中[16?17]。上述长度测试仪通过在被测系统的一端安装设备收发窄脉冲,并记该发送脉冲和反射回波脉冲的时间差,获得传输时延[16]。由于低压配电网存在多个节点和分支点,必然会产生多个反射回波脉冲,因此无法探测出图1所示T型分支结构的各段传输时延。UWB定位系统通过超窄脉冲的收发和已知的参考基站,计算出传输时延或者时延差,从而计算出地理位置,其脉冲宽度通常小于2 ns,不适用于电力线载波通信系统的频段要求[17]。
3) 基于扩频通信的时延测量技术[18]。它常见于全球定位系统。由于扩频信号具有良好的抗干扰性,因此其测量的精度更高,更适合于通信信道复杂的低压配电网中的端到端传输时延测量。
但GPS系统或者文献[18]均需要先对扩频信号解调,导致系统功耗和复杂度高,不适用于对功耗和成本敏感的低压电网。
2 智能低压电网分段时延测量算法
为了测量图1所示低压电网中典型T型网络各段传输时延t1,t2和t3,需要首先测量出AB,AC和BC的传输时延τ1,τ2和τ3。
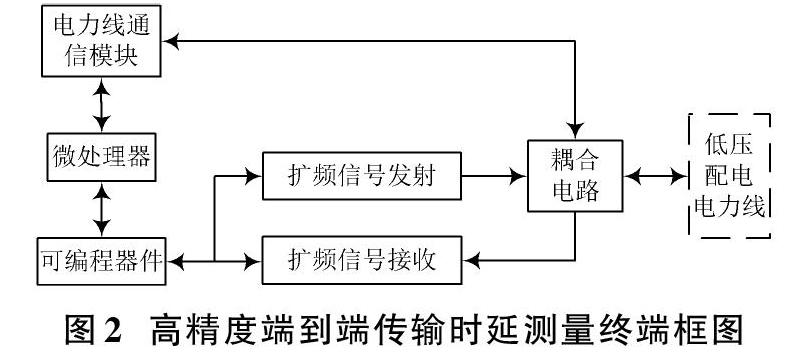
图2给出了所提的低压配电网高精度端到端传输时延测量算法运行的终端结构。
所提分段时延测量算法的流程描述如下:
1) 集中器通过电力线通信模块给节点A发送包含被测量的节点B时延测量命令;
2) 节点A的微处理器通过电力线通信模块向节点B发送时延测量命令;
3) 节点B的微处理器通过电力线通信模块给节点A回复测量确认命令;
4) 节点A的微处理器向其可编程器件发出时延测量开始命令;
5) 节点A的可编程器件产生测量信号,送给射频发射模块,并在测量信号全部发送完时,记录当前时间T1;
6) 节点A發出的测量信号,通过内部电路和电力线后,达到节点B的射频接收模块;
7) 节点B的射频接收模块将信号处理后,送给节点B的可编程器件;
8) 在节点B的可编程器件中,对接收到的测量信号进行识别后,立即将提前产生好的测量回复信号发送给节点B的射频输出模块;
9) 测量回复信号经过内部电路和电力线后达到节点A的射频接收电路;
10) 节点A的射频接收电路将接收到的测量回复信号处理后,送给节点A的可编程器件;
11) 节点A的可编程器件识别到测量回复信号到来后,记录此时的时刻T2,则传输时延:
[τ1=0.5(T2-T1-T处理)] (1)
式中,T处理为信号调制、识别、发送所花去的时间,它为一个确定值,与调制和识别算法、处理器运算速度、信号发送速率以及信号长度有关,可通过校准去除。节点A的可编程器件把测量结果τ1发送给节点A的微处理器;
12) 节点A的微处理器将测量结果,通过电力线通信模块向集中器汇报传输时延τ1;
13) 集中器收到τ1后,再通过电力线通信模块分别给节点A发送包含被测量的节点C时延测量命令,给节点B发送包含被测量的节点C时延测量命令,并由节点A和节点C、节点B和节点C配合完成上述过程,得到AC传输时延τ2,和BC的传输时延τ3;
14) 集中器利用式(2)计算出分段时延:
[t1=0.5(τ1+τ2-τ3)] (2)
[t2=0.5(τ1-τ2+τ3)] (3)
[t3=0.5(-τ1+τ2+τ3)] (4)
由于低压配电网存在白噪声、窄带噪声、周期干扰和随机脉冲噪声等多种噪声,为提高测量精度,必须选择抗干扰性强的测量信号和被测量信号。
鉴于扩频通信系统具有良好的抗白噪声、窄带干扰和随机脉冲干扰性能,本文选择扩频信号作为测量信号和测量回复信号。为提高时间分辨率,采用自相关性能良好的m序列伪随机码作为扩频调制信号。为解决低压配电网多个分支节点和终端对测量信号反射,导致测量模糊的问题,特选用m1序列的调制信号作为测量信号,m2序列的调制信号为测量回复序列,且m1和m2正交,保证了测量的有效性和准确性。
由于采用了伪随机码调制信号,测量信号属于扩频信号,可以以较低的功率发射,对电力线通信系统影响较小;同时电力线通信模块的通信信号对于测量系统是窄带通信信号,其信号对测量系统的干扰相当于窄带干扰,根据扩频通信技术特点,窄带干扰在扩频信号解扩时,会被大大降低。因此,本文所提的测量方法,可以与电力线通信系统共存。
本文选用BPSK调制方式产生测量信号[xm1(t)]和测量回复信号[xm2(t)]。式(5),式(6)中,m1(t)和m2(t)均为m序列。如图4所示,对测量信号和被测量信号的捕获,采用滑动相关法,其相关峰计算公式如式(5)~式(10)所示。
为降低系统复杂度,采用限幅放大1 bit采样对接收到的m序列调制信号直接进行相关运算,采用式(10)给出的均方根误差表征测量精度。
[xm1(t)=m1(t)sin(ωct)] (5)
[xm2(t)=m2(t)sin(ωct)] (6)
[Rymy′m(t)=12N-1k=-NNym(n)y′m(k+t+τ)] (7)
[ym(t)=1,-1, m(t)sin(ωct)≥0m(t)sin(ωct)<0] (8)
[y′m(t)=1,-1, m(t)sin(ωct)+n(t)≥0m(t)sin(ωct)+n(t)<0] (9)
[RMSE=1ni=1nτ2i] (10)
式中:[ym(t)]為本地存储的1 bit量化的m序列BPSK调制信号; [y′m(t)]为m序列BPSK调制信号经过信号之后的1 bit量化的序列;τ为传输时延;τi为第i次测量得到的传输时延。时延测量精度为采样率的倒数。
3 实验结果与分析
本节仿真分析不同噪声对测量系统精度的影响。仿真参数为:m1和m2选用15位的m序列,符号速率1 Mb/s,采样率100 MHz,载波频率4 MHz,测量分辨率为10 ns。
图5给出了无噪声干扰时1 bit采样的m序列扩频BPSK调制信号的相关峰。鉴于所提算法是对BPSK调制信号直接进行相关运算,且载波频率是扩频符号速率的4倍。因此在扩频信号滑动相关的过程中,2个码元(200个采样点)内,会出现7个相关峰。由于主峰的位置仍然表征了m序列BPSK调制信号对齐的时刻,因此可以用式(6)捕获正确的相关峰,从而计算出传输时延。
图6~图8给出了不同干扰下本系统的测量精度(m?code标识)。仿真次数为50次,判决门限为0.1,采用式(9)计算。为对比本文算法效果,在图中同时给出采用脉冲法测量时延的性能(Pulse标识),其中,脉冲宽度为10 ns,判决门限为接收信号最大值和最小值的平均值,重复次数和测量结果计算方式与本文所提算法相同。
由图6可知,由于扩频系统的良好抗干扰性,所提时延测量系统在SNR=-11 dB的白噪声下仍能达到10 ns的测量精度,相比脉冲法需要SNR>0 dB才能够实现10 ns的测量精度,性能提升了10 dB。因为两种算法都具有相同的时间分辨率,所以从图7中可以看出,所提算法的抗多径性能与脉冲法相近,在SIR =4 dB左右,可以达到10 ns的测量精度。图8中显示了所提算法在SIR=-3 dB时具有10 ns的精度,而脉冲法需要SIR>7 dB时才具有相同的测量精度。
4 结 语
本文研究并提出一种结合电力线通信模块和扩频通信技术的端到端时延测量技术。该技术利用电力线通信模块之间的相互通信,确定低压配电网中被测量的具体终端,结合T型网络结构特征,计算出低压配电网各分段之间的传输时延。
通过采用正交的m序列扩频作为测量信号和测量回复信号,并采用1 bit采样的m序列BPSK调制信号直接相关峰,实现了低复杂度、高精度、抗干扰强的时延测量性能。通过仿真论证了所提算法相比于传统脉冲法,性能得到了极大的提升。
注:本文通讯作者何先灯。
参考文献
[1] 雷锡社,刘敏.低压配电网通信技术及应用介绍[J].现代电子技术,2002,25(10):14?17.
[2] 李国华,白宝成,刘海龙,等.智能电网技术在电力系统规划中的应用研究[J].自动化与仪器仪表,2019(9):230?233.
[3] SCHWEFEL H P, ZHANG Y J A, WIETFELD C, et al. Emerging technologies initiative ‘smart grid communications: information technology for smart utility grids [C]// 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids. Copenhagen: IEEE, 2018: 124?131.
[4] GENG H. Engaging consumers in the smart grid marketplace [M]. Boston: Wiley Telecom, 2017.
[5] 李维嘉.河北地区用电信息采集系统的研究及应用[D].保定:华北电力大学,2018.
[6] WAERESCH D. Topology fault detection in low voltage grids based on statistical analyses of smart meter data [C]// 2016 IEEE PES Innovative Smart Grid Technologies Conference Europe. Ljubljana: IEEE, 2016: 1?5.
[7] 罗步升,林志超,何小龙.基于拓扑解析与深度学习融合的低压集抄系统故障诊断方法[J].电测与仪表,2018,56(20):145?152.
[8] 袁超.低压配电网络台区识别技术的研究与开发[D].大连:大连理工大学,2014.
[9] 薛军,王桃桃.一种通过电压特征区分台区和相别的方法研究[C]//2017智能电网新技术发展与应用研讨会论文集.南京:[s.n.],2017:350?353.
[10] 罗冉冉,龙磊,张垠,等.基于故障树理论的单相智能电能表黑屏故障分析方法研究[J].电测与仪表,2014,51(23):6?10.
[11] ZHANG Nan, SUN Yan, LIU Di, et al. FL?TN: a fault location algorithm based on tree topology for smart grid [C]// 2019 Chinese Control and Decision Conference. Nanchang: IEEE, 2019: 6221?6225.
[12] 张小博,王婷,佟芳,等.基于谱聚类的用电采集网络拓扑推断算法[J].电力信息与通信技术,2018,16(12):39?45.
[13] 张润生,李艳斌,李啸天.基于合并分层聚类的网络拓扑推断算法[J].电子学报,2013,41(12):2346?2352.
[14] 刘海客,李集林,尤启迪,等.一种基于OpenFlow协议的拓扑发现方法[J].电子设计工程,2016,24(13):116?119.
[15] 王睿,肖丽媛,曹苏苏,等.IP网络中端到端时延估计方法[J].北京邮电大学学报,2014,37(z1):97?103.
[16] 胡善江,贺岩,俞家勇,等.基于深度学习的脉冲激光测距回波时刻解算方法[J].中国激光,2019,46(10):203?211.
[17] 史刘强,付江涛.基于UWB定位系统设计[J].电子设计工程,2019,27(15):161?165.
[18] 刘松柏.群时延对扩频测距系统测距精度的影响[J].兵器装备工程学报,2017,38(5):118?122.
