大坝变形的多步预测模型研究

费 守 明

1 概 述

对于大坝变形问题，人们不仅关注以前发生的变形，更关注产生变形的原因和将来可能发生的变形，因此，大坝变形分析与预报具有广泛的现实意义。由于大坝变形分析的重要性、复杂性以及为了更准确、全面掌握大坝形态变化趋势，大坝变形预报模型一直在不断完善和发展。其中，回归分析是研究随机变量之间相关关系的一种方法，也是水工建筑物原型观测资料分析的常用方法[1-3]。它是应用数学方法对大量观测数据加以处理，从而确定变量之间的关系规律性，并用数学关系式表达出来。常规的回归模型容易受监测值系列中异常值的影响，因此，当测量值系列可能有异常值时，可将稳健回归应用于大坝变形预测。稳健回归包括多种模型，其中，加权最小二乘法，是将较小的权重赋给拟和较差的点。与一般的最小二乘回归相比，这种模型受异常值的影响较小[4-5]。但不论是常规的回归模型还是稳健回归模型，模型中的参数估计一般都采用回归分析方法，但这种方法有时会出现回归失败或模型预报精度不高等现象，从而不能满足工程要求。随着人工智能的发展，神经网络模型获得的广泛应用，目前人工神经网络应用的模型有若干种[6-8]，如Rumelhart 等的反向传播模型、Hopfield 的最小能量模型、Grossberg 的自适应共振模型以及Kosko 的双向联想模型等等，这些模型在网络构造、学习方式、学习规则、修正误差的传播方向等方面各有不同的特点，主要用途也各不相同。其中BP网络是Rumelhart 等人在1985 年开发出的一种多层前馈神经网络，其权值的调整采用反向传播的学习算法，是目前较为成熟并且应用最广泛的神经网络模型之一。

上述所建几类模型在大坝变形的单步预测中都取得了较高的预测精度，但对多步预测研究较少。在精度能够保障的情况下，预见期越长，对管理部门做出的决策时间越充分，能够较好较快地做出预防措施。因此，在实践中，多步预测比单步预测具有更高的理论研究价值和现实的指导意义。同时，这些模型都是根据气温、库水位、时效等变形因子来进行预测，在应用上也存在一定的局限性。如无论是神经网络模型，还是统计模型，因子的取法众多，温度、水位、时效等因子的组合也有多种方式，常常依赖经验。再者，未来一定时期内影响变形的因子是未知的，预报的时间就不能太长。基于此，本文把历史上观测到的位移值作为研究对象，分别建立线性回归模型、稳健回归模型和改进的BP 神经网络模型，在此基础上进行多步预测研究。

2 预测模型在二滩水库大坝变形中的应用

大坝变形过程中的定期变形监测时间序列蕴含了系统的演变信息，从这些数据中找到系统的演变规律，并对系统的发展趋势做出正确预测，是对大坝进行预警的关键所在。以二滩大坝拱冠测点CN8 的2004 年8 月16 日 至2007 年2 月28 日 共927 d 的水平径向位移为研究对象，其中以前600 d的位移数据建立模型，后327 d的水平位移进行检验。

2.1 时间序列的相关性分析

图1 是二滩大坝拱冠测点CN8 的2004 年8 月16日至2007 年2 月28 日共927 d 的水平径向位移过程，可以看出，位移总体上呈现周期为1 年的波动过程，局部具有锯齿现象，在序号为186，187 处出现两个变异点。大坝水平位移是受温度、水位及时效等多种因素产生的，其所观测的时间序列是上述影响因素的综合反映，相邻数据间具有很强的相关性。日水平位移时间序列具有很强的相依性，本文选取前12 d 的水平位移因子来预测步长为1～6 d 的水平位移。

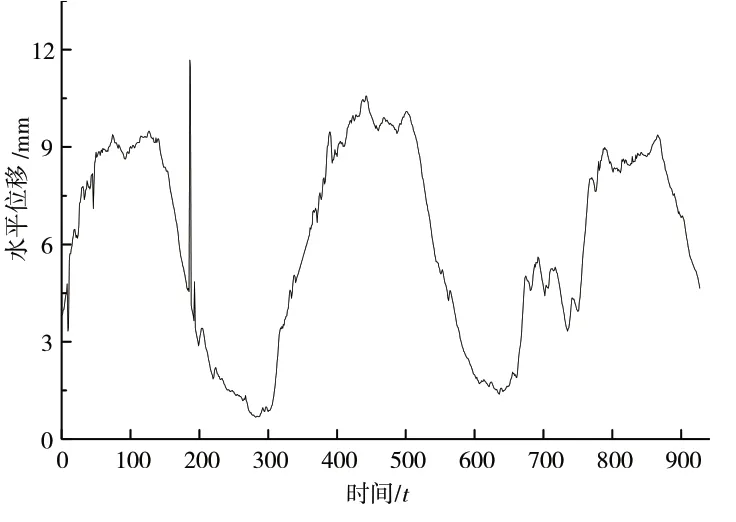
图1 测点CN8水平位移变化过程

2.2 多元回归模型的建立

根据多元回归模型原理，对水平位移时间序列建立的多元回归模型为：

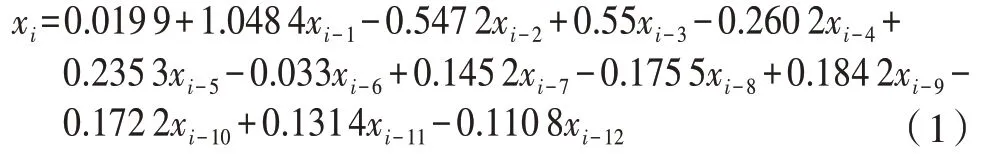
2.3 稳健回归模型的建立

在水平位移时间序列中，为了避免异常值的影响，建立了稳健回归模型。具体如下：

2.4 神经网络模型的建立

如前所述水平位移受多种因素影响，具有很强的非线性特点，因此，建立线性模型来对水平位移进行预测，具有一定的局限性。基于此，利用改进BP 神经网络原理，以前12 d 的水平位移作为神经网络的输入，隐层通过试算确定为20，输出向量是第13 d 的水平位移。即确定的神经网络结构为12-20-1。

2.5 预测结果分析

根据上述建立的多元回归模型、稳健回归模型和确定的神经网络结构分别对后327 个水平位移进行步长为1～6 d 的预测。图2 是3 种模型的拟和结果，可以看出，除了在变异点及其附近处的拟和误差较大外，3 种模型的拟和精度都比较高，拟和值非常接近实测值。预测结果如图3 所示（3 种方法的一步预测结果）和表1。可以看出，在步长为1 d的预测结果中，3 个模型的预测精度都很高，都属于精度较高的模型（通常认为：若绝对平均百分比误差小于10%，则模型预测精度较高）。其中稳健回归模型的预测精度最高，其统计的各种误差参数在3 个模型中最小，其次是多元回归模型，最后是神经网络模型。但随着预测步长的增加，3 种模型预测精度出现了相反的变化，神经网络预测模型的预测精度最高，在2 步到5 步预测值的绝对百分比误差都小于10%，完全满足预测要求。而多元回归模型在2 步以上的预测值的绝对百分比误差都大于10%。尽管在一步预测中，稳健回归预测模型最好，但在2 步以上的预测中，稳健回归模型预测的效果最差，总体上，它的预测值明显小于实测值，而且在2 步到7 步的预测误差统计中，各步的绝对平均百分比误差都大于10%。

图2 各种预测方法的拟和值

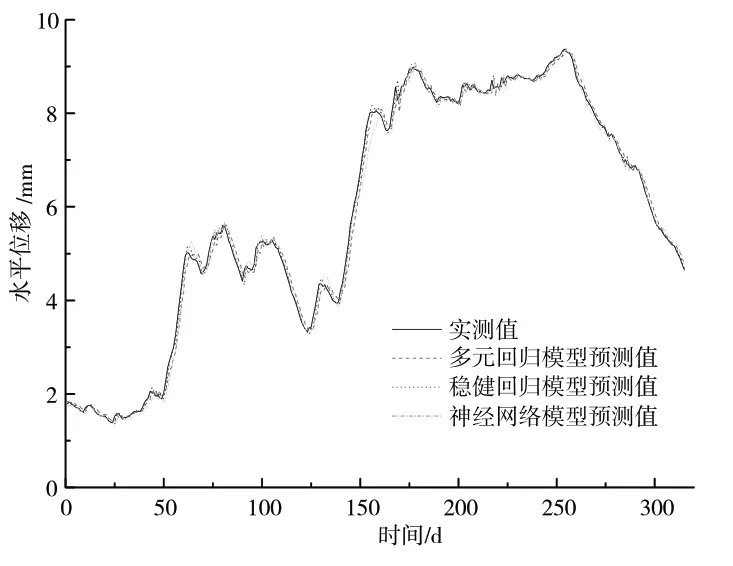
图3 各种预测方法的一步预测值

表1 各种预测方法的误差统计

3 结 语

已有的历史变形资料是各类影响因素的综合反映，故实际预测中采用同一位置的历史位移观测资料去预测今后一定时间内的位移值，这不仅符合预测的数学涵义，而且可以有效地减小预测数据采集的困难程度，提高预测精度及可信度，使得预测的可操作性加强。本文根据历史位移数据，采用统计模型及神经网络分别建立预报模型对水平位移进行多步预测，其方法是有效的，可以预测在边界条件未发生重大改变的情况下较长时间内的大坝变形，具有一定的拟和精度和泛化能力。其中，稳健回归模型和线性多元回归模型在预见期较短的时间里，预测精度最高；而神经网络模型抗干扰能力强，预见期较长。