First principles study of the electronic structure and photovoltaic properties of β-CuGaO2 with MBJ + U approach

Guoping Luo, Yingmei Bian, Ruifeng Wu, Guoxia Lai, Xiangfu Xu, Weiwei Zhang, and Xingyuan Chen,

1Department of Applied Physics, School of Science, Guangdong University of Petrochemical Technology, Maoming 525000, China

2School of Materials Science and Engineering, Chang’an University, Xi’an 710064, China

Abstract: Based on the density functional theory, the energy band and electronic structure of β-CuGaO2 are calculated by the modified Becke-Johnson plus an on-site Coulomb U (MBJ + U) approach in this paper. The calculated results show that the band gap value of β-CuGaO2 obtained by the MBJ + U approach is close to the experimental value. The calculated results of electronic structure indicate that the main properties of the material are determined by the bond between Cu-3d and O-2p energy levels near the valence band of β-CuGaO2, while a weak anti-bond combination is formed mainly by the O-2p energy level and Ga-4s energy level near the bottom of the conduction band of β-CuGaO2. The β-CuGaO2 thin film is predicted to hold excellent photovoltaic performance by analysis of the spectroscopic limited maximum efficiency (SLME) method. At the same time,the calculated maximum photoelectric conversion efficiency of the ideal CuGaO2 solar cell is 32.4%. Relevant conclusions can expand β-CuGaO2 photovoltaic applications.

Key words: first principles; β-CuGaO2; electronic structure; photovoltaic properties

1. Introduction

Oxide semiconductors generally have large band gaps,which can be widely used in thin-film transistors of the ultraviolet region, light-emitting diodes or transparent electrodes,etc.[1,2]. Most oxide semiconductors are not suitable for applications in solar cells and photocatalysis because they are almost transparent to visible light. Hexagonal ZnO and anatase TiO2are typical oxide semiconductor materials with band gaps of 3.37 and 3.2 eV, respectively[3,4]. However, the band gaps of Cu2O and wurtzite-derived AgGaO2are approximately 2 eV, which can be used to prepare solar cells and photocatalytic materials[5,6]. In 2014, Omata et al. of Osaka University prepared β-CuGaO2oxide semiconductors by ion replacement of NaGaO2materials[7]. β-CuGaO2is a direct bandgap material with a band gap of 1.47 eV, which is very beneficial for the preparation of a new type of photovoltaic material. Song et al. believe that β-CuGaO2also has ferroelectricity and could be potential ferroelectric photovoltaic materials by DFT research[8]. Currently, the popular ferroelectric photovoltaic materials such as BaTiO3and BiFeO3hold relatively large band gaps, low absorption of visible light, and low current density[9,10], while β-CuGaO2are expected to absorb more visible light to improve the efficiency of ferroelectric photovoltaics. Okumura et al. found that Cu vacancies as ptype intrinsic defect could be easily emerged in β-CuGaO2,and easily formed heterojunction semiconductors with ZnO[11]. It is necessary to introduce the Coulomb interaction parameter U into the Cu element to calculate the electronic structure for the 3d orbital of Cu ions is much localized and the traditional LDA and GGA calculated methods will underestimate the band gap[12]. However, Suzuki et al. calculated the band gap of β-CuGaO2with 0.3 eV by LDA + U (U = 6 eV) method, which is much smaller than the experimental band gap value of 1.47 eV[13]. The hybrid functional HSE and quasiparticle self-consistent GW are generally available for the accurate electronic structure relatively[14−16]. Okumura et al. calculated the band gap of β-CuGaO2by HSE method, and found that the band gap of β-CuGaO2is 1.09, 1.21, 1.56, and 1.96 eV respectively with the variational parameter α[11]. The band gap of 1.56 eV is the closest to the experimental value when the α parameter is 0.35[11]. They also calculated the band gap of β-CuGaO2with 0.84 eV by using the GW approach, which also deviated from the experimental value[11]. Furthermore,the computational costs of HSE and GW approach are relatively high. In this paper, the GGA + U and MBJ + U approach with low calculated cost have been employed to calculate the electronic structure of β-CuGaO2, and found that the calculated band gap obtained by MBJ + U approach is very close to the experimental value. On the basis of electronic structure calculation by MBJ + U approach, the spectroscopic limited maximum efficiency (SLME)[17]method was also used to calculate the photovoltaic properties of β-CuGaO2.

2. Theoretical model and calculated method

Fig. 1. (Color online) The structure of the β-CuGaO2.

Fig. 2. (Color online) The band gap values of β-CuGaO2 by GGA + U and MBJ + U method.

The calculations in this paper are carried out by the Vienna ab-initio simulation package (VASP) software package based on the density functional theory (DFT) theory[18,19]. We used the PBE functional[20]within the generalized gradient approximation (GGA) for exchange–correlation interactions. The cut-off energy is set to 520 eV and theK-point sampling in the Brillouin zone is adopted to 6 × 5 × 6. The energy convergence standard is 10–6eV and the Hellmann–Feynman force convergence criterion is less than 0.01 eV/ Å. The structure ofβ-CuGaO2is shown in Fig. 1. The calculated lattice parameters (a= 5.55 Å,b= 6.69 Å,c= 5.32 Å) are closed to the experimental values (a= 5.46 Å,b= 6.61 Å,c= 5.27 Å)[7]by GGAPBE functional. The 2H (hexagonal) and 3R (trigonal) CuGaO2are usually stable structures. The space group of the 2H phase is P63/mmc (No. 194) and 3R phase belongs to R-3m(No. 166) space group. The calculated energy difference between 2H and 3R CuGaO2is in the range of 5 meV/formula by GGA calculations. Theβ-CuGaO2belongs to Pna21space group (No. 33). The calculated energy ofβ-CuGaO2are higher than 2H and 3R CuGaO2with about 60 meV/formula.Theβ-CuGaO2could be a substable structure. To obtain more accurate electronic structure, the coulomb interaction parameterU[21]is added to treat the 3d orbital of Cu element based on the calculated structure of GGA-PBE functional.Based on the framework of density functional calculation, the modified Becke-Johnson potential plus an on-site CoulombU(MBJ +U)[21−23]approach was used to calculate the band structure and electronic structure ofβ-CuGaO2. Our calculated band gap ofβ-CuGaO2obtained by MBJ +Uapproach is much closed to the experimental value. In a similar situation,the Cu-based material Cu2X (X = S, Se, Te) is also calculated by MBJ +Uto obtain accurate band gap and electronic structure[24].

3. The calculated results and discussion

3.1. The band structure and electronic structure

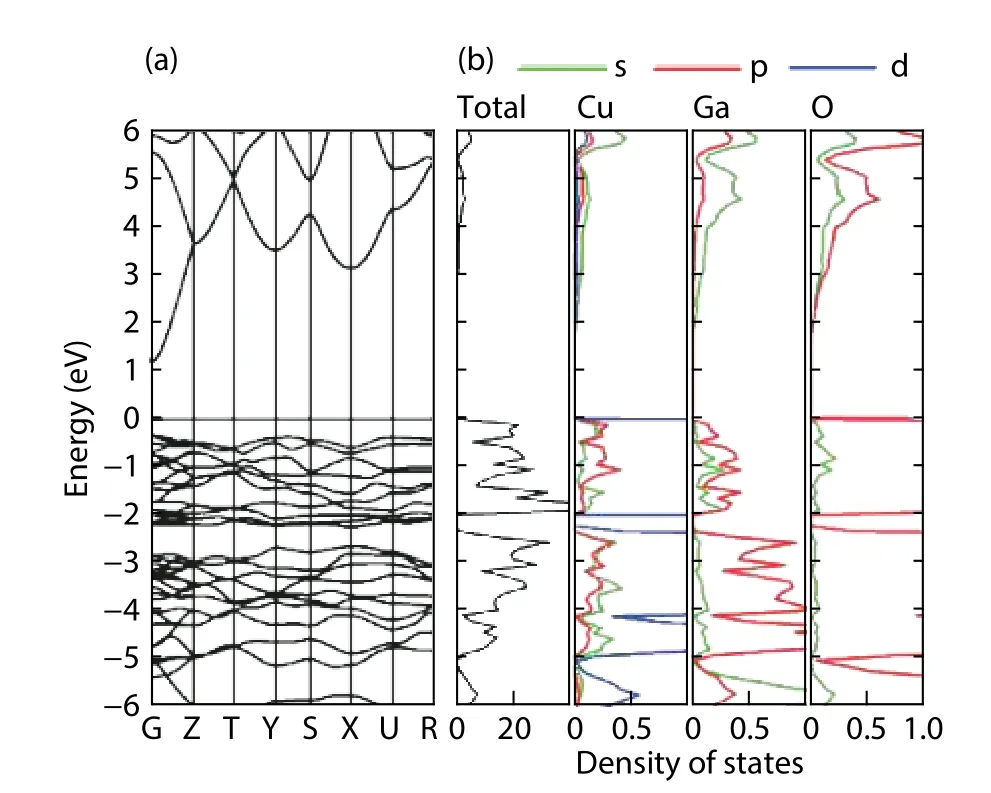
Fig. 3. (Color online) The band structure and DOS of β-CuGaO2.

As shown in Fig. 2, the calculated band gap value does not exceed 1 eV by GGA +Uwith the values ofUchanging from 4 to 10 eV, which is deviated from the experimental value of 1.47 eV. However, in the calculations of MBJ +Uapproach, the calculated band gap value is very close to the experimental value whenUtakes 7 and 8 eV. Finally, we select MBJ +U(U= 7.3 eV) approach, and the calculate band gap value ofβ-CuGaO2is 1.46 eV. In the calculation of the latter electronic structure, we all take the parameters of MBJ +U(U= 7.3 eV), which ensures the reliability of our calculation.

As shown in Fig. 3, the valence-band maximum (VBM)and the conduction band bottom (CBM) ofβ-CuGaO2are both at the G point, which indicated a direct band gap material. The curve near VBM is relatively flat, indicating that the effective mass of the hole is relatively large, while the effective mass of electrons is relatively small since the curve near CBM is steep, which is consistent with the early reported results[11,13]. The valence band level ofβ-CuGaO2is mainly caused by the Cu-3d energy level and the O-2p energy level and the hybridization between Cu-3d energy level and the O-2p energy level determines the main properties of the material. The density of states (DOS) is relatively small to form a weak antibonding orbital between O-2p energy level and Ga-4s energy level near the conduction band ofβ-CuGaO2. The transitions from the Cu-3d level to the O-2p energy level and the O-2p energy level to the Ga-4s energy level are prone to occur inβ-CuGaO2. These major energy level transitions will mainly affect the main optoelectronic properties ofβ-CuGaO2.

3.2. Optical properties

The absorption coefficients [α(E)] ofβ-CuGaO2were obtained by the following formula:

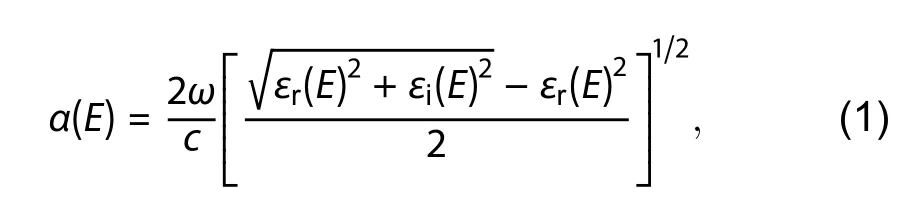
wherecis the speed of light in vacuum,ωis the incident light frequency. The imaginary and real parts of the dielectric function are expressed in terms ofεiandεr, respectively.Fig. 4 shows the calculated absorption coefficients spectrum ofβ-CuGaO2. The AM 1.5 solar spectral irradiance in the 300–1000 nm wavelength range is also shown in Fig. 4. It can see thatβ-CuGaO2exhibit high absorption coefficient up to 105cm–1in the visible region. The total fractional absorption(A) of incident solar radiation can be approximately expressed as following formula with the film thickness (d) and absorption coefficient [α(E)].

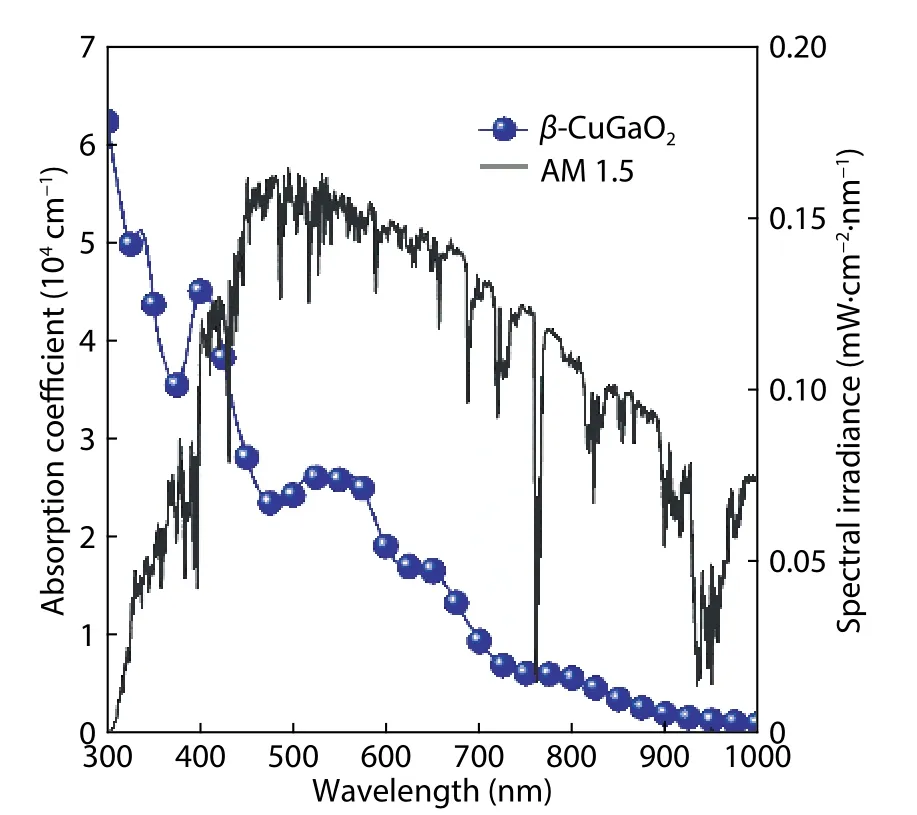
Fig. 4. (Color online) The absorption coefficient of β-CuGaO2 and AM 1.5 solar spectral irradiance in the 300–1000 nm wavelength range.

Fig. 5. (Color online) The optical absorption properties of β-CuGaO2.

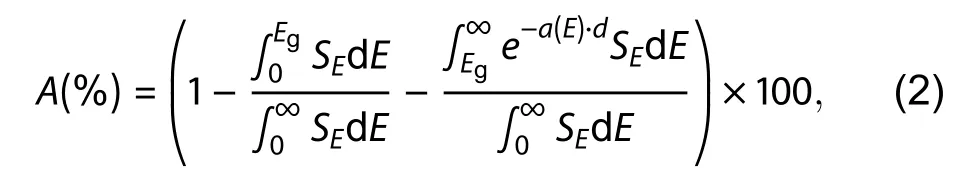
whereEgis the band gap andSEis the incident solar spectral irradiance changing with incident photon energyE. As film thickness ofβ-CuGaO2changes, the calculated fraction absorption of incident solar flux is shown in Fig. 5. As the thickness ofβ-CuGaO2thin films increases from 0.1 to 1μm, the total fractional absorption slightly increased, and then starts to saturate with thickness of 3μm.

3.3. Photovoltaic properties

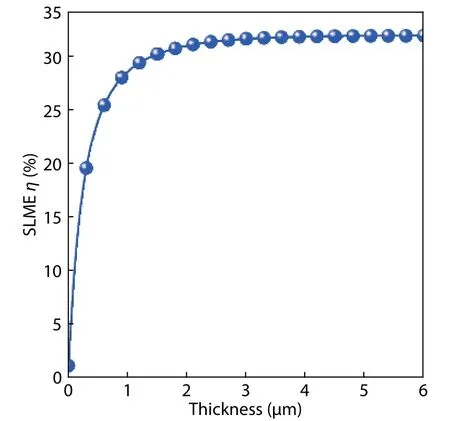
Fig. 6. (Color online) The SLME η as a function of film thickness for ideal β-CuGaO2 solar cell.

Fig. 7. (Color online) The current density–voltage (J–V) curves of the ideal β-CuGaO2 solar cell with a thickness of 3 μm.

The Shockley-Queisser limit indicates an absorber with bandgap nearby 1.4 eV has higher photovoltaic conversion efficiency[25]. The calculated bandgap ofβ-CuGaO2is 1.47 eV,showing that this material has the potential to an efficiency solar cell absorber. However, the thickness of the absorber layer,visible light absorption coefficient and carrier recombination are also important factors to the real cells’ efficiency. Therefore, the photovoltaic properties ofβ-CuGaO2are estimated by the spectroscopic limited maximum efficiency (SLME) metric proposed by Yu and Zunger[17]. The SLME efficiency forβ-CuGaO2thin films is shown in Fig. 6 with a function of thickness. We find that the SLME efficiency first increases rapidly with increasing film thickness. This mainly attribute to the increasing of film absorption. The SLME efficiency achieves maximum value as high as 32% at large film thickness. A layer thicknessL= 3.0μm is considered for the SLME calculation since beyond that value the efficiency is not noticeably changed whereas below that value. The typical current density–voltage (J–V) curves for theβ-CuGaO2are shown in Fig. 7.The photovoltaic parameters can be derived from Fig. 7, as shown in Table 1. For comparison, the photovoltaic parameters of theoretically and experimentally CdTe solar cells are also given in Table 1. Even though the open circuit voltage(Voc) ofβ-CuGaO2based photovoltaics cells is lower than the value of CdTe, but the conversion efficiency (η) and short circuit current density (Jsc) are much higher. These calculated results indicate thatβ-CuGaO2is a candidate for use as a highly efficient photovoltaic absorber material.

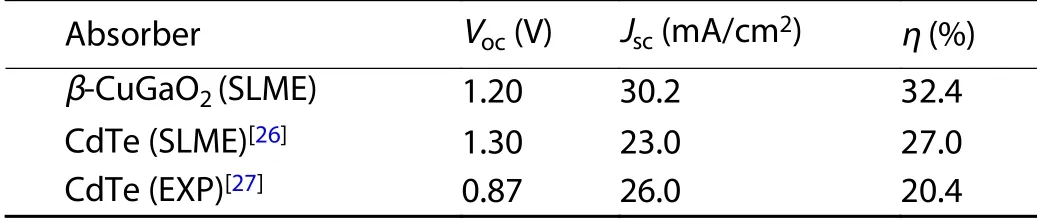
Table 1. The photovoltaic parameters of β-CuGaO2 and CdTe solar cells obtained by SLME method, the experimentally parameters for CdTe solar cells are also included for comparison.

4. Conclusions

In summary, GGA +Uand MBJ +Uapproach with lower calculated costs are employed to calculate the electronic structure ofβ-CuGaO2in this paper. It is found that the calculated band gap value obtained by MBJ +U(U= 7.3 eV) approach is closer to the experimental value. Near the top of the valence band ofβ-CuGaO2is mainly composed of the Cu-3d energy level and the O-2p energy level. The bond formed by the hybridization between Cu-3d energy level and the O-2p energy level determines the main properties of the material. When the thickness ofβ-CuGaO2film is increased from 0.1 to 1μm,the total absorption of the film increases sharply. The total absorption becomes to saturation when the film thickness is about 3μm. The photovoltaic performance parameters of ideaβ-CuGaO2solar cells are calculated by the SLME method,which indicated that it could reach 32.4% energy conversion efficiency. By comparison with photovoltaic parameters of CdTe thin film solar cells, it was found thatβ-CuGaO2could be a potential high-efficiency photovoltaic material.

Acknowledgements

This work was supported by the NSFC (Grant No.11547201), Natural Science Foundation of Guangdong Province, China (Grant No. 2017A030307008), Natural Science Basic Research Program of Shaanxi (Program No.2019JQ-380), and Natural Science Foundation of Guangdong Petrochemical University of Technology, China (Grant No.2017rc20).