基于ATM Optimized拓扑下末级叶片变工况的气动特性与静力分析的数值研究
2020-10-22张济凡宋立滨康剑南
张济凡,宋立滨,康剑南
(1.大唐东北电力试验研究院有限公司,吉林 长春 130012; 2.大唐长春第二热电有限责任公司,吉林 长春 130012)
0 引言
供热机组的深度调峰迫切需要解决热电解耦问题。热电解耦技术是热电联产机组供热过程中,通过增大中压缸抽汽,使低压缸叶片在小容积流量下运行,保证发电能力的前提下满足供热需求。
然而,在冬季取暖期间,机组受到“热电耦合”的限制,并且其参与电网调峰的能力非常有限,这大大降低了系统的灵活性。对机组的安全运行和发电公司的经济影响较大[1-3],同时机组在低压缸切除改造后末三级叶片在低负荷工况下长时间运行,对于低压缸后末三级叶片安全运行有很多风险。
电厂在低压缸切除改造时,由于升高了低压末级叶片动应力,致使叶片发生破坏,所以需要对低压缸排汽容积流量进行限制,要求叶片在长期运行时,容积流量区间内动应力大小要满足强度与振动设计要求,西屋公司在1969~1971年间执行研究计划发现,其单级的叶片动态应力在可变负荷的小容积流量区域中出现“突然增加现象”,小容积流量下叶片的动应力约为设计值的5到10倍,如图1所示。

图1 变负荷动应力曲线
1 末级叶片不同负荷下的流体计算
考虑到我国200 MW以上机组能参与调峰[4-7],在用电波谷阶段,机组运行小于设计负荷。风冷型机组的负荷变化直接影响流过的蒸汽流量,而水的温度和末段压力的转变最终会影响容积流量。中间级的蒸汽提取加热也会导致热电联产过程中的级后的体积流量小于设计的体积流量。风冷型机组的末段压力会随动于大气,当其压力高于出厂值时,低压缸最终流量将小于出厂值。在此基础上,对末级叶片进行CFD流体数值计算、静应力进行分析等工作,使之满足设计要求,以保证运行稳定[8-9]。
1.1 几何模型
计算选取730末级通流部分为计算域,几何模型见图2,循环对称图形见图3。

图2 叶片整圈模型
图3 循环对称模型
1.2 网格划分
叶片网格均采取ATM优化拓扑(ATM Optimized)架构,经由对照H/J/C/L-Grid拓扑网格与ATM优化拓扑网格,可以看出ATM优化拓扑网格的正交特性更好,并且易于调整。但另一方面,网格数比H/J/C/L-Grid拓扑结构多20%左右,以满足计算精度要求。为了在模拟工作条件下准确捕获诸如涡旋状态和位置之类的信息,并在给定计算范围内网格节点的数量情况下,综合考虑各种低压水平下动叶片和静叶片的特定高度,节点约450 000左右。
1.3 边界条件
利用总能量方程处理数值计算部分,利用SST模型方程中的高阶精度迎风差分方法处理湍流模型。
如表1所示。对于这种差别,本文所采用的高精度差分方法综合了二者的长处。可在不同的流动条件下,对于入口边界条件,给出了总温度和总压力。

表1 模型对比
1.4 网格无关性验证
为了准确模拟不同工况气动特性,理论上应尽量提高网格数量,差分方程将变成微分方式,数值解更为精确。考虑到算力水平,不可能无限划分网格,取而代之的是采取合理的网格数目。在对工程问题的数值模拟中,当网格数增加到某一数值后,再增加网格数量,计算结果的变化越来越小甚至不变,这时我们通常的做法是选择比这一数值稍大一点的网格数量对实际工况进行数值模拟,节省计算时间和计算资源。本文将静动叶计算域分别划分成10万、20万、25万、30万、40万、60万、95万网格,进行数值仿真计算,采用进出口总压差值作为参考值对网格无关性进行验证。从图4中可以发现,静动叶计算域网格在40万以上进出口总压差基本不变,因此在保证计算结果准确性的条件下,为了节省计算资源和提高计算效率,静动叶流计算域取约45万网格数。

图4 静叶和动叶网格数量与出口压差变化
2 气动计算结果
2.1 不同工况下气动计算结果及分布
以下分别列出各个工况的计算结果。
(1)叶片流线图(THA工况)
图中可知,额定工况下,在进汽小圆处有略微正攻角,叶片未出现涡流现象,流线由入口平滑稳定地过渡至出口,流动分离现象并未明显的出现在内吸力面。
(2)叶片马赫数分布(THA工况)
从THA工况下的马赫数分布图可知,气体在动叶通道内流动较为稳定,在通道喉部位置速度达到最大,而后开始逆压流动。
与图6中的结论保持一致的是,未出现显著的流动分离是因为逆压段相对较短。

图5 动叶各截面流线图

图6 动叶各截面马赫数分布图
(3)叶片极限流线图分布(THA工况)
如图7所示,极限流线除了局部位置,其余位置彼此接近平行,这说明了压力面上边界层的流动为二维流动。

图7 动叶极限流线分布图
通过对极限流线图中吸力面的观察,我们可以发现,叶片显示中的大多数的极限流向基本上是平行的,显示出二维流动的特点,但在端部区域被三维分离线包围。通道涡流和吸力面与端壁的交点,极限流线的特征表明端区流具有三维性。
(4)背压4.9 kPa、30 t/h工况叶片流线图
如图8所示,当条件为4.9 kPa、流量为30 t/h时,此时末级动叶处于小流量高背压,此时容易形成流动分离,而且也容易造成回流现象。在叶片通道的大部分区域出现涡旋,且叶中部位的涡旋最大。

图8 动叶各截面流线图
(5)背压4.9 kPa、30 t/h工况马赫数分布
图9中可以看出,在叶栅通道内,特别是中截面附近,存在高速涡旋,一方面会大大降低叶片效率,另一方面会耗散气体能量。

图9 马赫数分布图
(6)背压4.9 kPa、30 t/h工况叶片极限流线图

图10 动叶极限流线图
从图中可知,在动叶的压力面和吸力面,流线都不是接近平行的,而是相互掺混的,这也在一定程度上印证了上述流线图和马赫数分布图的结果。
(7)背压2.2 kPa、40 t/h工况叶片流线图
如图11所示,该工况下,进汽小圆处有些许正攻角。现在40 t/h,相对于额定工况流量较小,这在一定程度上减小了正攻角。但在顶截面附近,叶片压力面有少许分离。

图11 动叶各截面流线图
(8)背压2.2 kPa、40 t/h工况马赫数分布图

图12 马赫数分布图
与额定工况相比,气体最大速度位置在动叶通道内前移,这使得气体在较长的逆压段流动,这种情况,会对叶片气体分离起到促进作用。
(9)背压2.2 kPa、40 t/h工况叶片极限流线图
如图13所示,除局部位置外极限流线保持平行,证明了二维流动的观点。同样,观察极限流线图中的吸力表面上,我们可以发现:叶片显示中的大多数极限流向基本上是平行的,显示出二维流动特点。三维分离线包围端部。通道涡流和吸力面与端壁的交点,极限流线的特征表明端区流具有三维性。

图13 动叶极限流线图
(10)背压2.2 kPa、30 t/h工况叶片流线图
图中可知,与额定工况相比较,中截面以下的正攻角有所改善,但是在中截面以上,叶片的压力面存在比40 t/h工况更大的分离。

图14 动叶各截面流线图
(11)背压2.2 kPa、40 t/h工况马赫数分布图

图15 马赫数分布图
从图中可知,最大马赫数较40 t/h工况有所前移,这使得该工况下的逆压段更长,这对于叶片表面气体分离起到了促进作用。
(13)背压2.2 kPa、30 t/h工况叶片极限流线图
如图16所示,动叶片压力面极限流线在大部分区域已不再接近平行,比40 t/h工况的流动更加恶劣。

图16 动叶极限流线图
2.2 气动计算总结
经对4种工况叶片气动计算,得到了末级在不同工况下的三维流线示意图,如图17~图20所示,从THA工况、背压2.2 kPa、40 t/h工况、背压2.2 kPa、30 t/h、背压4.9 kPa、30 t/h工况依次顺序,随着流量不断降低,动叶表面的气体脱离表面的程度逐渐加大,动叶通道内的流动不断恶化。

图17 THA工况

图18 背压2.2 kPa、40 t/h工况

图19 背压2.2 kPa、30 t/h工况

图20 背压4.9 kPa、30 t/h工况
3 末级叶片静应力分析
3.1 计算所需参数
本文所需末级叶片信息如表2所示,材料信息如表3所示。

表2 叶片参数

表3 材料参数
3.2 模型计算
本文所用的计算模型如图21所示,采用循环对称发来对整圈装配进行模拟。
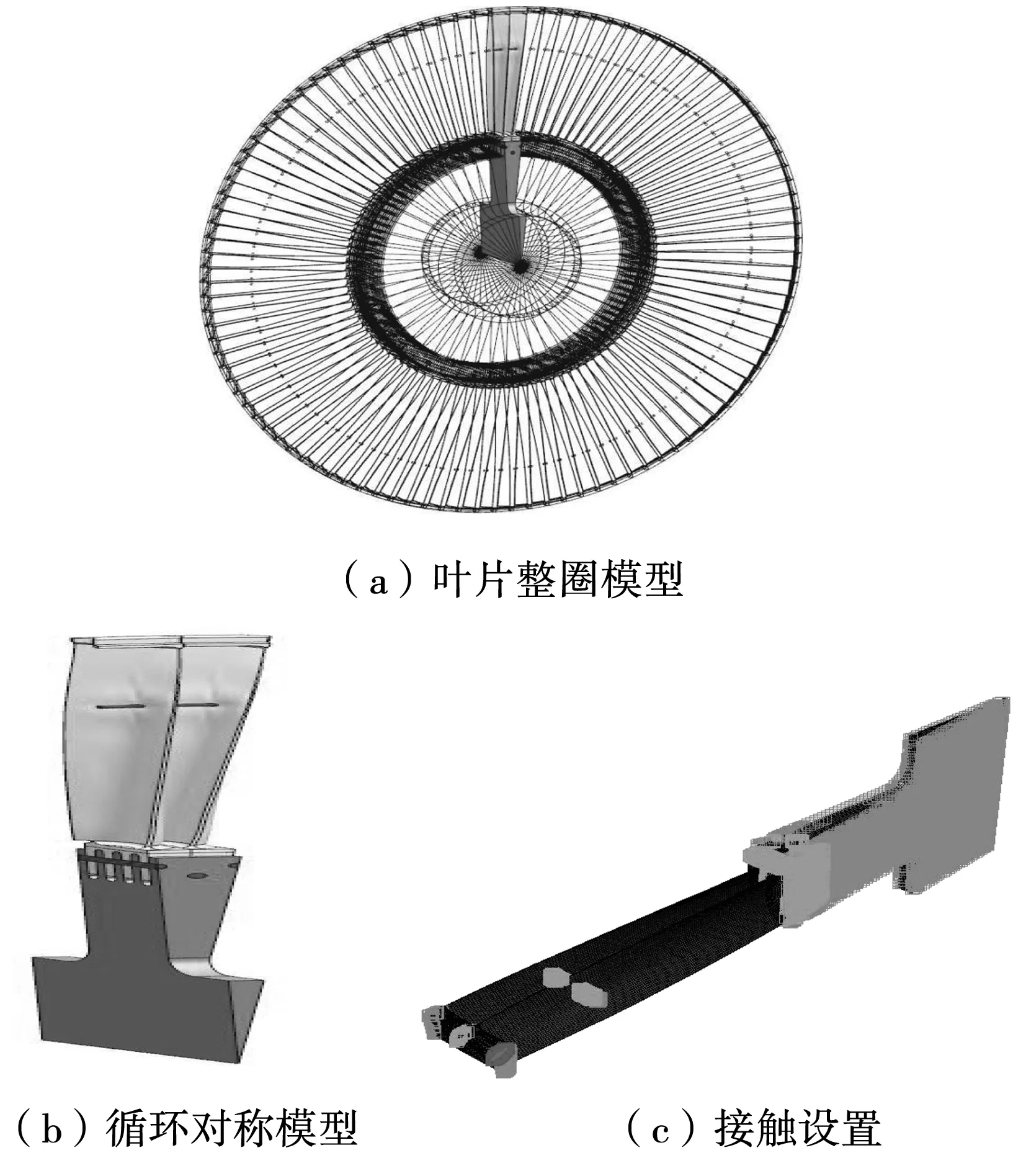
图21 计算模型
3.3 边界限制
该计算模型边界条件如表4所示。

表4 叶片参数
将上述限制值施加至模型的边界条件中,即可完成整个模型的给定。
3.4 叶片静应力分析结果

图22 计算模型整体应力云图

图23 A叶片应力云图(背弧侧、内弧侧)

图24 B叶片应力云图(背弧侧、内弧侧)

图25 B叶片应力云图(背弧侧、内弧侧)
经叶片应力结果所示,其峰值销钉孔位置,最大值应力比许用值为0.68,轮槽最大值应力在轮槽销钉孔位置,最大应力/许用值为0.68。
4 结论
针对热电解耦技术应用于火电机组深度调峰而引起低压缸叶片的小容积流量安全运行问题,本文采用ATM-Optimized拓扑结构结合CFD数值模拟方案,对末级通流计算域进行变工况气动特性及静应力分析,其结论如下:
(1)随着流量不断降低,动叶表面的气体脱离表面的程度逐渐加大,动叶通道内的流动不断恶化。小流量高背压时,通道内的气体脱流分离较为明显,涡旋在几乎整个叶高部分掺混,气体流动严重恶化,同时会引起鼓风效应。
(2)经对叶片有限元静应力分析,得到叶片应力结果,根据材料的许用应力以及叶片静应力考核准则,叶片静应力满足设计要求,且根据叶片峰值应力/许用值大小可以得到,叶片静应力满足低压缸切缸工况。
本文对调整汽轮机低压缸趋于最小流量运行、提高机组经济性,且具有推广意义。
