基于暂态特征的广义电力负荷参数辨识方法研究
2020-10-22都小利
程 琳, 都小利, 钱 文, 徐 华
(1.安徽电气工程职业技术学院, 安徽 合肥 230051;2.国网安徽省电力有限公司培训中心, 安徽 合肥 230022;3.国网亳州供电公司, 安徽 亳州 236800)
0 引言
近年来,随着特高压交直流在我国以及其他许多国家和地区电网中的大力地推进,以及新能源分布式发电的大力发展,对大电网的实时控制变得越来越复杂[1]。由于电网本身电路状态的复杂性,以及电网的运行状态的时变性和负荷状态的随机性,这都使得电网具有复杂的动态特性[2]。目前,负荷建模的研究落后于电力系统其他部件的建模,严重制约了电力系统的健康和可持续发展。负荷特性的差异性,一定程度上影响了电力系统研究中的暂态稳定和电压稳定[3]。在复杂的动态特性下,研究负荷参数辨识方法,使电网能稳定运行具有重要的意义[4]。因电力系统负荷的不确定等特性,研究时不易精准模拟各节点负荷和节点电压,所以开展负荷建模是一项研究难点。文献[5]提出静态负荷模型也称为ZIP模型,即恒阻抗、恒电流、恒功率模型。文献[6]提出感应电动机的并联静特性下的负荷结构模型,该模型符合多数应用场合下的负荷特性。但在分布式电源比例较大或离负荷母线较近时,会给系统带来比较大的计算误差[7]。
为更好地表示广义电力负荷的各种特性,本文提出基于暂态特征的广义电力负荷模型。该模型利用大电网中关键节点电压变化的特性作为负荷动态特性的等效值,通过区间联络线的功率波动、关键节点的电压变化来实时表征等效负荷的动态特性,同时利用动态负荷的计算、灵敏度最高的联络线下的母线线电压来表征等效发电机的动态特性和一系列负荷参数的特性量。
1 含感应电动机的等值负荷模型
电力系统负荷模型通常被等效为为一个动态模型和一个静态负荷模型,等值的静态负荷模型一般用多项式模型表示,如式(1)所示。
(1)
式(1)中V为实际运行电压;P0、Q0是当电压V等于额定电压V0时的有功功率和无功功率,称为额定负荷功率;P、Q为负荷实际消耗的功率;ap(aQ)、bp(bQ)、cp(cQ)为负荷有功(无功)功率的系数,分别代表负荷的恒定阻抗、恒定电流、恒定功率部分的比例,它们之间满足ap+bp+cp=1,aQ+bQ+cQ=1的关系式。该模型也称为ZIP模型,即恒阻抗、恒电流、恒功率模型[8]。
负荷的动态模型可以等效于感应电动机模型,在d,q旋转坐标系下的感应电动机的模型如式(2)所示。
(2)

(3)
式(2),式(3)中iq、id和uq、ud分别为d,q的电流和电压,RS、Lq、Ld分别为定子绕组的电阻和d,q轴的电感,Ψf、Ψq、Ψd分别是励磁磁链和定子在d,q磁链的分量,ωe为转子的电角速度。由于感应电动机在实际负荷中占很大比例,相对于其他部件而言,感应电动机对电力系统的影响也很大,因此在计算和分析中,我们通常将负荷模型等效为一个感应电动机和一个静态负荷的等值静态模型。随着新能源和智能微电网的发展,受端电力系统中包含大量电源,电网结构更加复杂。对于这种既有电力系统电源并且仍然以电力负荷为主的区域电网系统,称为广义电力负荷,其模型结构称为广义电力负荷模型[9,10]。
2 广义电力负荷模型
广义电力负荷模型在含感应电动机的等值负荷模型的基础之上加入了同步发电机,从而展现电力系统负荷模型的发电特性。广义电力负荷模型如图1所示。图1中枢纽母线连接了静态负荷和感应电动机以及同步发电机的模型。我们考虑配电网支路的广义电力负荷模型时,除了在含感应电动机的等值负荷模型系统中加入等值的同步发电机之外,还加入了一条母线UI,母线UI与电路实际母线US之间的阻抗需要阻抗匹配,否则当虚拟母线等值电压UI与实际母线电压US不等时,线路就会被烧毁甚至被击穿。考虑配电网支路的广义电力负荷模型的简化图为图2所示。图2中加入了一条虚拟母线UI并且配上配电网等值阻抗,加入了三相变压器以及电容,与原母线相连的有配电网无功补偿、等值静态负荷、等值电动机和等值发电机。

图1 广义电力负荷模型 图2 考虑配电网支路的广义电力负荷模型
3 负荷模型参数求解
在电力系统暂态稳定中我们主要关注功角稳定,也就是说,如果在某一个时刻,当电力系统中遭到一个很大的扰动时,发电机的输入功率和输出的电磁功率将失去原有的平衡,从而直接引起发电机的转速和发电机的转角发生变化,各发电机之间会相互的震荡和摇摆。因此我们在暂态稳定下分析广义电力负荷模型就首先需要在电力系统模型中保证功角平衡。
在同步发电机建模中,我们从惯量中心的理论出发,我们可利用加权聚合法将某一部分区域的一群同步发电机等效为一个同步发电机进行等值测量。式(4)和式(5)分别是发电机等效的时间常数和等效的暂态电抗的计算方法。
(4)
(5)

(6)

在受端电力系统模型中功率输入进入电力系统的受端的观测线路中总共有五条,分别是线路1、线路2、线路3、线路4和线路6,我们将这五条线路等效为外部电源,而从电力系统中受端流出的功率线功率输出联络线为线路5,因此将线路5等效为广义电力负荷,在计算等值的广义电力负荷中需减去或加上相应的部分,除此之外,我们也假设这些线路1、2、3、4、6它们是虚拟断开的,也就是它们并互不相连,但是我们在第一步中提到了线路2要予以保留,所以按照上图电力系统下的受端系统的流向示意图列写公式,可以得到式(7)。
SLeq=SL+S5-S1-S2-S3-S4-S6
(7)

图3 等效系统潮流流向示意图
其中:SLeq为系统等效广义电力负荷模型;SL为系统实际负荷;S5为同步发电机模型,其余为联络线传输功率。为较好地描述系统在电压、频率变化较大情况下的广义电力负荷特性,本文原始负荷SL使用差分方程负荷模型,如式(8)所示。
Y(k)=ay1Y(k-1)+ay2Y(k-2)+bu0U(k)+bu1U(k-1)+bu2U(k-2)
(8)

4 仿真分析
3机10节点的系统原始图形如图4所示。在该等值的系统中参数分别为:
(1)变压器LTC1:525/13.8 kV,X=0.003 p.u.,分接头变化范围为500~550 kV,基本运行状态下变压器分接头位置为533 kV。
(2)变压器LTC2:525/115 kV,X=0.003 p.u.,分接头变化范围为500~550 kV,基本运行状态下变压器分接头位置为530 kV。
(3)变压器LTC1:115/13.8 kV,X=0.001 p.u.,分接头变化范围为103.5~126.5 kV,基本运行状态下变压器分接头位置为112.1 kV。
(4)变压器T4:13.2/540 kV,X=0.002 p.u.。
(5)变压器T5:13.2/540 kV,X=0.0045 p.u.。
(6)变压器T6:13.2/530 kV,X=0.00625 p.u.。
(7)发电机1:平衡节点,V=0.98 p.u.。
(8)发电机2:PV节点,V=0.964 p.u.;无功功率极限为200~725 Mvar。
(9)发电机3:PV节点,V=0.972 p.u.;无功功率极限为200~700 Mvar。
(10)500 kV输电线路:Z=0.0015+j0.02880 p.u.,B/2=1.173 p.u.。
(11)如图4中所标的数据中,并联电容器的无功功率值对应于相应的额定工作电压。
等值发电机群的参数为:
1号机:无穷大母线;
2号机:H=2.09,MVA容量=2200 MVA;
3号机:H=2.33,MVA容量=1400 MVA;
电机阻尼转矩系数D=2.0。
利用这些数据对电路进行搭线和仿真,搭线图如图5所示。
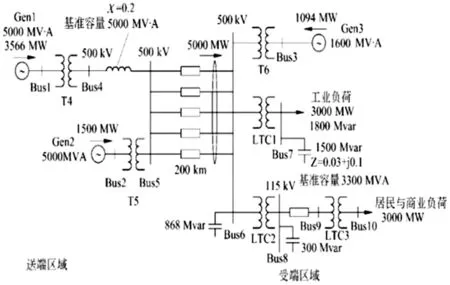
图4 3机10节点的原始状态搭线图

图5 3机10节点的PSASP的仿真搭线图
辨识后得到的参数为:
ay1=0.9024,ay2=-0.4306,bu0=0.7806,bu1=0.2012,bu2=0.0732
在Bus2母线上调节电压降为10%,再进行仿真。将获得的参数带入模型进行验证,有功功率仿真结果如图6所示,无功功率仿真结果如图7所示。
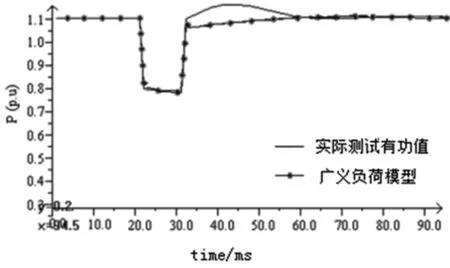
图6 广义电力负荷模型有功功率响应 图 7 广义电力负荷模型无功功率响应
从图6和图7的广义电力负荷模型辨识出的参数拟合曲线与实际曲线比较,广义电力负荷的动态辨识特性较好,通过广义电力负荷模型辨识出的参数拟合的有功功率曲线和无功功率曲线接近实测得到的负荷有功无功数据。
5 结论
本文研究了考虑配电网支路的广义电力负荷模型,在负荷模型中不仅考虑了静态负荷,感应电动机动态负荷,还考虑了同步发电机的相关参数。通过暂稳分析模型对广义电力负荷模型进行简化,将其简化成成含同步发电机的动态负荷求解,从而使得模型参数求取方便。利用3机10节点系统仿真,模型通用性强,且电路简单方便理解,该简化模型的仿真结果和实际测量值间误差较小。
