基于IDA分析的城市轨道交通高架区间桥梁性能化抗震设计研究

陈志辉

摘 要：《城市轨道交通结构抗震设计规范》GB50909-2014提出的基于转角的性能化抗震设计方法，不能考虑横向两柱或多柱以及纵向连续刚构等非悬臂式桥墩构件的轴力变化对桥梁弯曲变形的影响。本文基于增量动力分析法（（Incremental Dynamic Analysis，IDA）对某（42+70+42）m连续刚构进行了性能化抗震设计研究，计算结果表明，若不考虑轴力的变化，可能会高估地震作用下结构的承载力、刚度和耗能能力，甚至导致不安全的设计计算。基于IDA的抗震设计方法，也为这类桥墩构件的性能化抗震设计提供了重要借鉴。

关键词：性能化抗震设计，截面纤维模型，滞回特性，非线性时程分析，增量动力分析

Study on performance based seismic design of elevated bridge of urban rail transit

Chen Zhi-hui

China Railway Eryuan Engineering Group Co.， Ltd.， Chengdu 610031， China

Abstract： Code for seismic design of urban rail transit structures（GB50909-2014）has proposed performance-based seismic design method based on cross-sectional bend corner. However， it cannot consider the influence caused by the change of axial force on the bending deformation of the bridge， such as horizontal two column or more column and continuous rigid-framed bridges which have often involved significant axial force changes introduced by earthquake. Based on Incremental Dynamic Analysis method， the paper proposed performance-based seismic design of a 42 + 70 + 42 m continuous rigid-framed， the calculation results show that it may overestimate the bearing capacity， stiffness and energy dissipation capacity of the structure if to omit the variation of axial force， and even lead to unsafe design. Seismic design based on IDA can provide an important reference for this kind of bridge.

Key words： performance based seismic design; section fiber model; hysteretic characteristics; nonlinear time-history analysis; incremental dynamic analysis

0引 言

2014年12月起实施的最新国家标准《城市轨道交通结构抗震设计规范》GB50909（以下简称《规范》[1]）对新建或改建的城市轨道交通结构提出了基于性能的抗震设计（Performance Based Seismic Design）。与传统基于承载力和刚度的抗震设计方法相比，基于性能的抗震设计能够使设计人员有效地把握不同地震水准下的结构性能，也便于区别对待现代结构设计中業主的不同要求。以重点设防的城市轨道交通高架区间桥梁结构为例，其核心即是在E2和E3地震作用下（即设计地震和罕遇地震）应允许结构进入弹塑性工作阶段，特别的是在E3地震作用下要实现结构不能出现局部或整体的倒毁，为达到该抗震性能要求，需要对遭受E2和E3地震作用的高架区间桥梁结构进行变形验算。

变形验算或基于位移的抗震设计是基于性能的抗震设计的核心内容，其关键是为不同地震水准下的结构设定合理的变形或位移容许值，并能够准确地计算出不同地震水准下结构的真实地震反应，从而判断结构的抗震性能。《规范》将结构构件的转角（即计算假定结构最终是发生弯曲破坏）作为结构变形验算的控制指标，与美国Caltrans Seismic Design Criteria[2]和 AASHTO Guide[3]以结构位移为控制指标的抗震设计方法相比，转角控制指标计算方法省去了由转角积分计算结构位移的过程，便于设计操作;同时，计算的转角延性系数通常大于位移延性系数，设计偏于安全。

根据《规范》附录G的规定，对于钢筋混凝土构件的弯曲变形能力，应基于材料的标准强度，由截面的弯矩-曲率分析得出（见图0-1）。截面弯矩-曲率分析中所用轴向力，应根据地震时可能存在的荷载作用进行内里组合得到。对于高架区间标准简支梁和仅设一个制动墩的节点桥桥墩而言，若不考虑罕遇地震作用下的列车竖向荷载作用，该轴力即为恒载作用下的轴向力。那么这类悬臂式的桥墩构件塑性铰区的曲率分布可简化为线性分布，如图0-2所示，对塑性铰区各截面曲率沿塑性铰区长度积分可得到塑性铰区转角，按照（式0-1）确定截面屈服点和极限变形点的转角：

在确定结构的抗震设计变形容许值时，应充分考虑不同的地震作用水准并留有一定的安全冗余度，《规范》规定按照下式确定E1、E2和E3地震作用下的结构构件的转角容许值：

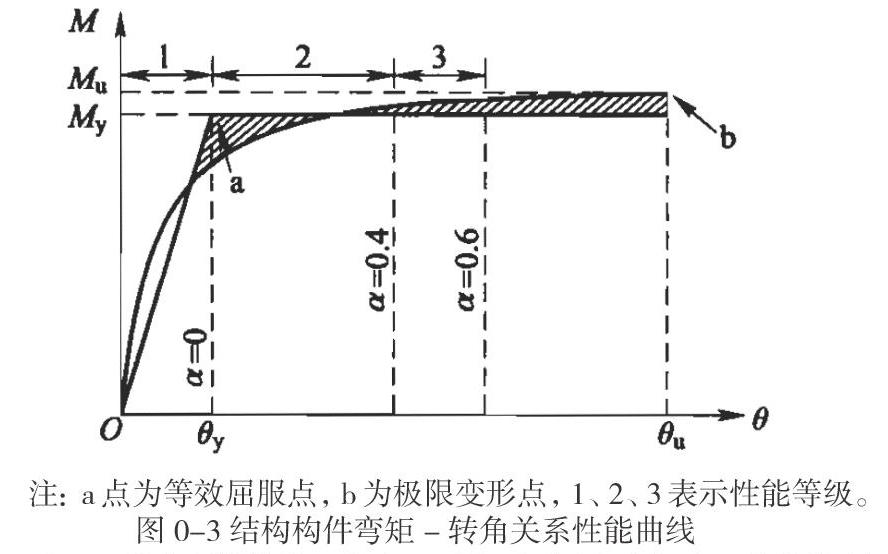
其中，为性能等级系数，对于重点设防类高架区间结构，E1、E2和E3地震作用下分别取值为0、0.4和0.6，K为构件极限塑性转角的安全系数，可取1.5。因此可按照构件的弯矩-转角曲线关系确定结构构件的能力曲线、性能点和性能等级（见图0-3）。

对于悬臂式桥墩构件，其在地震作用下轴力为恒定，构件控制截面的曲线是唯一确定的。因此可以根据弹性阶段分析得到的截面配筋和轴力，确定结构构件在弹塑性工作阶段的弹塑性铰特性，然后由弹塑性反应谱法和（或）动力时程分析法计算出结构构件控制截面在不同地震水准下的弯矩和转角，即可在表征构件抗震能力的曲线上找出其性能点，从而确定不同地震水准下的结构性能等级。

然而，对于横向两柱或多柱以及纵向连续刚构等桥墩来说，在地震作用下，由于受到动轴力的影响，导致其轴向力不断变化。首先，已有的研究表明[4]，若不考虑轴力变化，可能会高估地震作用下结构的承载力、刚度和耗能能力，甚至导致不安全的设计计算。其次，这里非悬臂式桥墩，在受到非恒定轴向力的耦合作用影响时，将导致其构件截面关系曲线跳跃性变化，而并非唯一确定的。为了考虑动轴力的不利影响，需要在计算中不断更新最不利轴力，对构件的截面关系进行迭代计算，反复循环更新构件轴力和根据截面关系曲线确定的弹塑性铰特性，直到结构构件的关系曲线与计算的轴力基本吻合为止。这种方法直接导致计算代价偏大，不便于工程设计实践运用。然后，这类桥墩构件在地震作用下，墩底和墩顶都是潜在塑性区，都可能进入弹塑性状态，沿构件全长的曲率分布不再是图0-1所示的线性分布，因此也不能直接按照（式0-1）计算出构件的转角。可见，对于非悬臂式桥墩，《规范》基于截面转角的性能化抗震设计方法的操作性较差。此时为了简化设计计算，可以参照以转角代替位移的做法，偏保守地以截面曲率代替转角，采用曲线来评价地震作用下的结构性能，即图0-3中转角以曲率代替。为了计算的可靠性，该性能曲线的计算应该充分考虑轴力变化的影响。

为了考虑轴力变化对结构构件弯曲变形能力带来的影响，可以采用增量动力分析法（Incremental Dynamic Analysis，IDA），即动力推覆分析。Berterro[5]提出的增量动力分析是采用将同一条地震波按强度幅值逐级增大进行一系列的非线性时程分析，提取各次时程分析得到的最大反应数据组成能够反应不同强震作用下结构刚度、强度以及变形能力的变化全过程的地震响应曲线，因此可以更全面、准确地评价地震作用下的结构抗震性能，时程分析过程中也能够全程考虑轴力变化的影响。研究表明[6]，若采用结构第一周期的谱加速度值Sa（T1）作为地震动强度指标，逐级增大某一地震波的强度幅值，能够有效地避免以峰值加速度PGA作为强度指标，不同地震波输入下结构响应曲线离散性较大的缺点。

本文以某一城市轨道交通工程（42+70+42）m连续刚构为例，根据Midas软件基于IDA分析对其进行性能化的抗震设计，并与恒载轴力的计算结果进行比较说明了轴力变化对结构承载力、延性和变形能力的影响不可忽略。

1计算模型

1.1结构布置及配筋

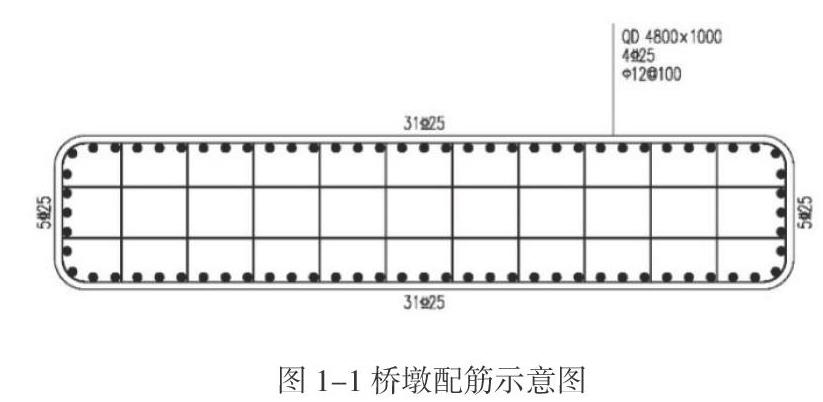
某城市轨道交通工程高架区间（42+70+42）m连续刚构，采用双柱式薄壁墩，支点梁高为4.2m，跨中高度为2.1m，过渡段按照二次抛物线变化，独立承台群桩基础。工程场地抗震设防烈度为Ⅶ度，场地类别为Ⅱ类，场地特征周期Tg=0.45s。轨道交通列车为中国B型车，六辆编组，最大轴重P=140kN，空车轴重Po=80kN，桥面二期恒载按照90kN/m。根据运营阶段和E1地震作用工况进行结构的强度（或承载力）设计，桥墩的配筋如图1-1所示。地震工况下，采用土弹簧模拟桩土相互作用，弹簧刚度参数根据“m”法确定，不考虑边界阻尼对抗震设计的有利因素。

1.2材料本构关系

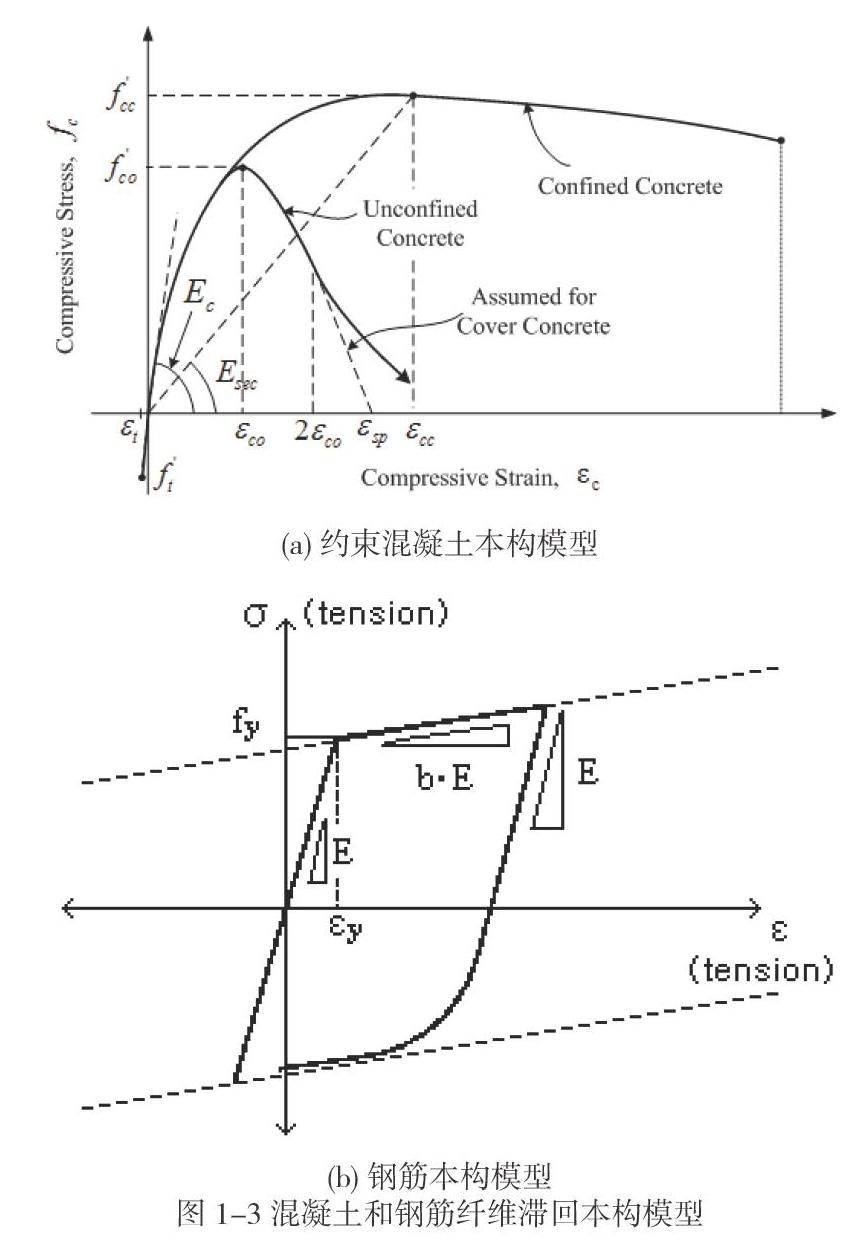
在地震作用下，桥墩钢筋可能发生屈服，外层混凝土开裂甚至压碎，且连续刚构桥墩受到的轴力将发生变化，轴力与弯矩之间的耦合关系，会直接影响桥墩弯曲承载力和变形能力。采用基于材料本构模型的钢筋混凝土杆件纤维模型，能够较准确的分析此类结构的高度非线性问题。纤维模型是将构件截面划分成若干的的混凝土纤维和钢筋纤维，根据平截面假定，计算截面的曲率和各个纤维的应变，然后由所得的各个纤维的应变根据钢筋和混凝土的滞回本构模型，计算出纤维应力，最后积分得到截面的弯矩和轴力。本文计算中，混凝土纤维本构模型采用Mander约束混凝土和非约束混凝土模型分别模拟箍筋约束区混凝土和保护层混凝土，钢筋纤维采用Menegotto-Pinto模型（見图1-3）。由于采用了较准确的材料本构模型，可以较好地模拟钢筋混凝土构件在复杂轴力下的弯曲强度、延性和滞回行为。也可以在分析过程中自动计算出潜在塑性区截面的塑性铰特性，而无需在非线性时程分析时，事先根据一个确定的轴力由截面弯矩-曲率分析得到截面的塑性铰特性，再根据计算后得到的变化的轴力更新该塑性铰，依次循环迭代直到满足误差要求。

2增量动力分析

2.1分析工况

本文选取适用于Ⅱ类场地的两条实际地震波San Fernando和Northbridge地震波，以及一条人工地震波进行IDA分析，以结构第一周期的谱加速度值Sa（T1）作为地震动强度指标，按照步长0.2m/s2逐级增大，每条地震波进行了15步计算。计算中采用杆件纤维模型定义构件的弹塑性铰特性，进行非线性时程分析。

2.2结果分析

时程分析中，对应的E1、E2和E3地震作用下，桥墩最不利的曲率延性系数如图2-1所示。计算结果表明，在E2和E3地震作用下，桥墩墩顶进入弹塑性工作阶段，与悬臂式桥墩构件潜在塑性区位于墩底的结论截然不同。在E3地震作用下，桥墩墩顶最大曲率延性系数为1.74。

取三条地震波IDA的计算结果的平均值，得到评价结构抗震性能的曲线。将（式0-2）中的转角以曲率代替，计算出分别计算出E1、E2和E3地震作用下的结构构件曲率性能等级界限值。将E1、E2和E3地震作用得到的性能点标注于该曲线上，如图2-2所示。结果表明，在E1、E2和E3地震作用下，构件性能等级分别为1、2和2，满足规范要求。与恒载作用下得到的截面相比，可知：根据IDA计算时，考虑了动轴力引起的桥墩轴力变化，轴力变小的影响较明显，使得桥墩截面的轴压比降低，极限承载力降低的同时延性有明显的改善，但根据恒载轴力计算结果高估了桥墩的承载力，而低估了桥墩的延性和耗能能力。该计算结果表明，在非悬臂式桥墩的性能化抗震设计中，桥墩受动轴力的影响不容忽略。

3結论和建议

通过对某城市轨道交通工程（42+70+42）m连续刚构的基于IDA的性能化抗震设计研究，可知：

（1）该桥墩在E1、E2和E3地震作用下分别满足性能等级为1、2和3的规范最低要求，具有较好的抗震延性和耗能能力。在大地震下，结构的承载力和延性相对适中;

（2）IDA计算结果与恒载轴力下的计算结果对比表明：非悬臂式桥墩构件受到动轴力的影响，其承载力降低，延性有明显改善，在抗震设计中应充分考虑动轴力引起的桥墩轴力变化的影响。

在横向两柱或多柱以及纵向连续刚构等桥梁的性能化抗震设计中，应充分考虑动轴力引起的桥墩轴力变化的影响，为简化抗震设计，建议参照文献[4]，引入等代轴力法进行设计，按照能量等效的原则，将变轴力等效为恒定轴力进行抗震设计计算。

《规范》提出的性能化抗震设计是基于构件的变形性能，对于静定的悬臂式桥墩构件，某一构件的抗震性能即可表示整个结构的抗震性能。然而，对于连续刚构、高架车站等超静定结构，存在较多的冗余约束，其结构整体的抗震性能或安全储备可能大于单个构件的抗震性能或安全储备。对于这类结构的抗震设计，目前的《规范》存在诸多不足，尚应进行深入研究。

参考文献：

[1]GB 50909-2014，城市轨道交通结构抗震设计规范[S].

[2]Caltrans Seismic Design Criteria[S]， V1.6， 2010.

[3]AASHTO Guide Specifications for LRFD seismic Design[S]， LRFDSEIS-2， 2011.

[4]汪训流，陆新征，叶列平. 变轴力下钢筋混凝土柱的抗震性能分析， 工业建筑，2007，37（12）：71～75.

[5]Berterro V.V. Strength and deformation capacities of building under extreme environments， Instructural Engineering and Structural Machanics [M]. Pister K.S.（ed.）， Prentice-Hall： Engewood Cliffs， NJ， 1977.

[6]Dimitrios Vamvatsikos and C.Allin Cornell. Incremental Dynamic Analysis， Earthquake Engng. Struct. Dyn.， 2002， 31（3）： 491～514.