基于本质内涵 探究定理意义
2020-10-21朱红娟
朱红娟
摘 要:学习最重要因素是意义。“理解规则概念,获得方法策略,体验思考价值,感受学习愉悦”等是数学学习的意义所在。真正的数学教学,需要立足本质内涵,把教学目标变为学习目标,把学习目标变为任务驱动,回归有意义的数学学习,实现课堂的突围。本文试着提出课堂突围方向:基于学情现状的重新审视,走近起点,课堂真实自然;基于核心目标的深度扣问,拉长体验,课堂深入厚实;基于学习差异的现实存在,求同存异,课堂鲜活多样等实施策略,课堂才能因走向意义而彰显厚度。
关键词:小学数学;定理;探究;本质内涵
数学新课程提倡“淡化形式,注重实质”,数学呈现给我们面前的是符号世界、规律世界,让学生经历数学活动的过程,体验数学思考方法的重要性……这些都是数学教学的意义所在,回归意义需要策略实施。在小学数学知识体系中,数学定理是十分重要的组成部分。对于数学定理的教学,要基于对学习内容所蕴含的教学价值、思维水平以及所蕴含的育人因素进行合理的解读,设计有价值的学习活动,引导学生经历数学定理的探究过程。以下,我结合《三角形三边关系》一课的教学来谈一谈。
一、基于学情现状,找到真实起点
数学学习是基于经验又超越经验的一种方式,数学学习也需要有一种理性、探究的精神。产生有意义的学习是需要学生能力与经验相匹配。因此,在小学数学教学中,把握学生的学情现状是十分重要的,这样,才能找到他们真实的学习起点。
在教学《三角形三边关系》一课时,通过前测的策略对学生真实的学习起点进行把握的。我设计了以下三道前测题:
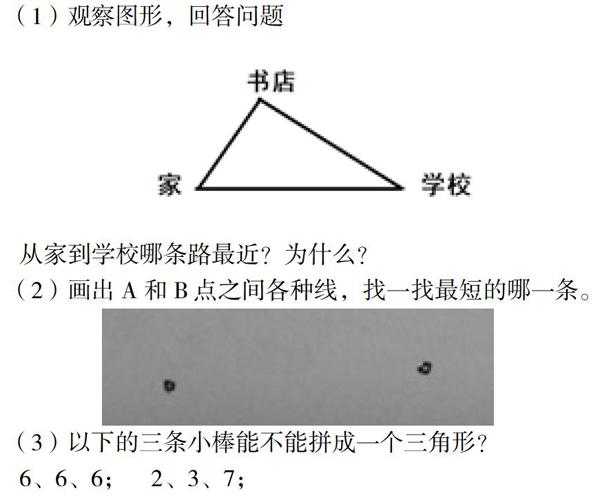
(1)观察图形,回答问题
从家到学校哪条路最近?为什么?
(2)画出A和B点之间各种线,找一找最短的哪一条。
(3)以下的三条小棒能不能拼成一个三角形?
6、6、6; 2、3、7;
这样的前测是基于3个方面的思考:衔接维度,判断能否组成三角形的与两点之间线段最短之间是否已经建立联系;知识维度,学生是否知道判断三条线段能否组成三角形的一般方法吗?学生是否知道三边关系理论依据实质是两点之间线段最短;能力维度:发现三角形三边一般关系。从一般到特殊,发现最简便方法,最短两边之和大于第三边规律。
1.改辙易途,对接经验真实自然
“一切关于实在的知识,都是从经验开始,又终结于经验。” 三角形三边关系教学学生起点在哪里,是我们制定教学目标的参考依据,寻找最真实的起点,对接起点,让课堂的自然而真实。对学情现状再审视,基于学生已有经验的了解,从活动设计等等进行一些改变,改辙易途,才显自然和从容……
这样的开展,基于学生的学情分析,改变了过去一直是由三条小棒拼三角形,现在提供一些周长都是12厘米的三角形,因为学生对于能否判断能不能围成一个三角形不是空白的,这样的教学改变了过去一味的“拼”,这样的设计原本就是让孩子们认识到周长一样的三角形的由于三边长度不同形状也是不同的,但是弊端也是显而易見的,只有三边可以围成三角形的,那么不能围成的三角形呢,缺失对比,课堂空间太小,必须要改辙易途……
2.固本正源,借力猜想任务驱动
追寻意义引领下的课堂需要把目标变为任务,把知识变成问题,把方法变为问题,这是数学课堂的愿景。三角形三边关系的发现和理解需要合理体验途径,这样的发现也不是一蹴而就的。量一量一个三角形三边的长度,这样的体验空间是否太小,倒过来去试去想,给予学生的想象和思考空间也许会更大,课堂需要固本正源,基于这样思考,第二次教学设计这样展开的:
片段:用12厘米的可折叠细铁丝围成一个三角形,你觉得三边可能是多少?(每边长度取整厘米数)
生1:4、4、4;
生2:3、4、5;
生3:1、4、7;
生4:5、5、2;……
让学生来猜一猜12厘米铁丝围成的三角形三边可能会是什么情况,由于是同一根铁丝围成的三角形,总长是相等的。这样的设计,在学生理所当然的认为无论怎么分都是可以围成三角形,事实上但是由于分成不同的长度造成不同的结果,有的是不可以围成三角形的,聚焦冲突,借力猜想,激活后面深入研究……
二、基于目标引领,经历体验过程
思考是数学教育的本真,借助三角形的三边关系,凸显数学思考价值取向。寻找到三角形三边本质关系,实现动态过程,是实现课堂厚实的有效手段之一。拉长过程尽显过程,让课堂实现冲突与思考、探究与反思、意义因对话而获得,意义因体验而获得,从形式走向本质……
1.提领而顿,聚焦核心高峰体验
课堂需要确定核心目标,课堂需要围绕这个核心深挖隐藏在背后的数学思想,经历体验和感悟的过程,聚焦课堂的生长点,在学生经验的冲突点中追寻意义,在思维冲突中回归理性。聚焦核心经历点,提领而顿引领高峰体验,使体验学习到新的高度……
数学需要理性的思考,怎样思考,一一列举,慢慢寻找,课堂也就有了底蕴。
通过操作让学生明白其内涵,才是数学课堂的本质和任务所在,并能经过分析充分地表达出来.“经历就是最美的风景”,经历了方法寻找、方法的验证、把课堂的有限空间尽最大努力创设最大的空间,数学理性思考得以彰显……
2.本立道生,实现从本到意突围
课堂学习需要从关注知识结构走向数学思想的体验,不满足知识的掌握,把数学思想与方法作为引领教学的根本,本立道生,让数学思想显现出来,改变课堂教学形态,让数学学习彰显数学思想的力量。
片段之四:那么7+3>2,是不是也可以围成一个三角形呢?那不也是两边之和大于第三边吗?(这样的引导让学生们不得不去思考问题究竟在哪里?)
生1:是哦,好像不行哎
生2:老师,我发现有的三条线段有2组线段之和大于第三条边的
生3:老师老师,我知道,不能只看其中两条边相加和大于第三边,那得必须要每两边相加与第三边去比大小,如3+4>5 3+5>4;4+5>3都存在,所以可以围成一个三角形;
师:那能不能重新概括一下呢?谁能完整的说一说着其中的规律?
生4:应该是任意两边之和大于第三边,这样的三条边能够组成三角形的。
师:三角形任意两边之和大于第三边,还有其他理由来解释吗?
……
生5:像上面的三角形中,我们可以把线段AB 看作是A和B之间的距离,A点经过C到 B也可以看作A和B之间的距离,我们已经知道了两点之间线段最短,所以BC+AC〉AB;
生6:这样还是不完整的,还要这样想我们可以把线段AC 看作是A和C之间的距离,A点经过B到C也可以看作A和C之间的距离,我们已经知道了两点之间线段最短,所以AB+BC〉AC;同样的AB+AC〉BC......
生7:老师,两点之间的线段长度要比两点之间的折线要短,两点之间线段最短(掌声响起......)
师:判断能不能围成一个三角形,看来大家都掌握了,如果每次都这样有没有觉得有点麻烦,能不能改进一下使得更为方便呢?
生8:只要较短的两边之和大于第三边就可以了……
同样一根铁丝分成不同长度造成不同的结果,能围成的三角形其中2边之和大于第三边发现与不能围成三角形的也有其中2边之和也有大于第三边的,聚焦冲突,形成任意两边之和大于第三边规范的规律;这样太麻烦有没有更好的,逐渐形成到最短两边之和大于第三边的最简规律发现;可谓“一路坎坷”,体验是充分的。从一般到最好,学生在课堂历经“磨难”,课堂收获的不仅仅是本位的知识,更是实现思想充分体验的目标,课堂教学得以实现从本到意的突围。
三、基于学情差异,组织分层学习
追寻有意义的数学课堂,必须是开放和动态的,学生是一个个不同的生命体,学习是不同学生用不同的思考方式参与进行中,这样的课堂教学如果我们用相同的课堂教学目标来衡40分钟的达成是否合理,是不符合不同的人学不同的数学。课堂需要直面学生存在的差异,让差异成为课堂的资源。
1.和而不同,适度超越各有提升
课堂需要根据不同学生的不同水平,让差异在课堂显现,让课堂不再仅仅是一种声音,让个别差异视为教学的组成要素.让不同的孩子尽最大可能的发展,课堂的目标定位取决于课堂的品质,数学课堂的思维纵深引领需要在三角形三边关系教学不能仅仅满足于以上的流程和目标定位,还需要具有和而不同,承认和尊重差异,求同存异中合理的超越.
2.联想衍生,由此及彼见木成林
数学课堂需要抓住本质核心不变,引领课堂的深入。数学课堂的同样需要充分运用学生的差异存在,激活孩子自己去联想,进一步引领孩子们自己去思考,培养孩子思考问题的发散性,实现见木成林的理想效果。也许学生的问题当时他们无法解答,但是孩子的不同思考角度,多问一句你还能想到什么,让不同层次的孩子自己来说,由此及彼的整体思考,衍生的是一种学习方式,实现意义课堂。
通过这一堂课的教学,让我深刻体验到了数学课堂意义突围蕴涵在每一个在每一个数学定理的探究之中,蕴涵在每一个数学问题的研究之中。“课堂意义回归是教学设计的重要组成部分,在基于对教学内容蕴含的教育价值理解的基礎上,设计了相应的师生共同参与的学习活动,课堂是有预谋有计划的学习活动,课堂也是在基于学习过程的教学目标下牵引下,课堂过程充分展开,深入高效。数学教学中最有价值的行为数学思考是,提出基于意义回归,因为挖掘核心概念蕴含的数学思想,我们的课堂让每一个学生经历感悟和体验的过程。彰显了生命力的课堂是因为有问题、有思考、才会有思想,才会有数学的本质和价值。
参考文献
[1] 张丹《发展学生基本活动经验的探索与实践》[J]小学数学教师 2014年第3期P4-P7
[2] 胡典顺《基于数学意义的数学教学改革研究》[M].华中师范大学出版社2011年6月第一次出版 P249-P258;P67
[3] 董静《高品质课堂创新案例研究(小学数学)》[M].教育科学出版社2014年9月第一版p7
