坝基弹性模量对广源拱坝动力特性影响分析
2020-10-21覃振威张小飞何飞龙黄佳敏
田 羽,覃振威,张小飞,何飞龙,黄佳敏
(广西大学土木建筑工程学院,南宁 530000)
0 引言
桂林市资源县广源水电站位于广西东北部资源县河口乡境内的五排河上,是一座以发电为主,兼有向漓江补水、防洪、旅游等综合效益的中型水利水电工程。工程主要建筑物包括水库大坝、引水隧洞和发电厂房。大坝采用混凝土双曲拱坝,高坝方案最大坝高95.00 m。坝址的下游两岸基本对称且无较大的冲沟,岸坡自然坡角约45°,坝区河流呈SN 向,宽高比2.35~2.38。坝基岩体为硅化泥岩,属中硬岩,河床坝段以厚层状为主,两岸坝肩及下游抗力体则以中厚层状为主,地层倾向右岸偏上游,局部有泥化夹层。坝址所在区域的地震基本烈度为Ⅵ度,拱坝按Ⅵ度地震设防。虽然地震设防烈度不高,但考虑到坝体的最大坝高接近100 m,而且坝顶溢流坝段沿轴线方向宽度相对较大,堰体悬出上下游坝面较多,坝体的震动对坝的安全有较大影响。此外,坝基岩体风化、卸荷总体程度较强,弱风化层厚度较大,BII类或BIII类岩体的变形模量差异较大,因此,有必要研究坝基岩体变形模量变化对拱坝动力特性影响,为拱坝的布置提供依据。
1 方法与模型建立
在拱坝动力响应计算中,目前常用的方法有振型分解反应谱法和动力时程分析法,前者能求解结构在弹性条件下的最大动力响应,后者能得到结构随时间变化的动力响应,两种方法常常同时采用,相互补充。
1.1 振型分解反应谱法
振型分解反应谱法[1,2]假定结构是线弹性多自由度体系,利用振型分解和振型正交性原理,将求解个n 自由度弹性体系的最大地震反应,分解成求解n 个独立且等效的单自由度体系的最大地震反应,根据求得每一个振型对应的地震作用效应,采用一定的组合方法将每个振型的地震作用效应组合成总的地震作用效应。振型分解反应谱法可以通过统计的方法得到标准反应谱,避免了地震加速度记录的困难。
根据反应谱理论,结构各阵型的最大地震反应与相同自振周期的单自由度体系的最大反应成正比:
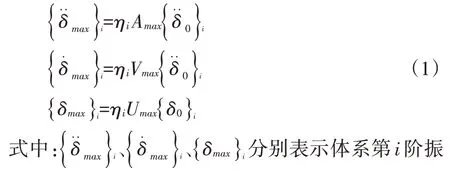

式中:SE为地震作用效应;Si、Sj为第i 阶、第j 阶振型的地震作用效应;m 为地震采用的振型数;ρij为第i阶和第j 阶振型的相关系数;ζi、ζj为第i 阶和第j 阶振型的阻尼比;γω为第j阶和第i阶圆频率比。
1.2 时程分析法
地震动三要素为振幅、频谱和持时,反应谱法虽然能同时考虑结构各频段振动幅值的最大值和频谱两个要素,却没有明确反映出“持时”。地震时程分析法[3]则是根据选定的地震波,采用逐步积分的方法对动力方程(7)进行直接积分,从而得到结构在地震过程中每一时刻的位移、速度和加速度反应。

1.3 计算模型的建立
为分析坝基不同部位的弹性模量变化对拱坝动力特性影响,将坝基在高度方向按坝顶以上(Ⅰ区)、两岸坝肩(Ⅱ区)、河床坝基(Ⅲ区)水平划分为上、中、下3 个区域。分析中坝体混凝土弹性模量Ec 取为定值,为Ec=25.5 GPa(相应于C20 混凝土),采用不同的坝基弹性模量Er 与坝体混凝土弹性模量Ec的比值来反映坝基弹性模量的变化,计算考虑了4种方案,①方案一:保持Ⅱ和Ⅲ区坝基弹性模量不变,且Er/Ec=1,Ⅰ区坝基弹性模量按Er/Ec=0.1、0.2…1、1.2、1.5、2、2.5、3、3.5、4 改变;②方案二:保持Ⅰ和Ⅲ区坝基弹性模量不变,且Er/Ec=1,Ⅱ区坝基弹性模量按Er/Ec=0.1、0.2…1、1.2、1.5、2、2.5、3、3.5、4改变;③方案三:保持Ⅰ和Ⅱ区坝基弹性模量不变,且Er/Ec=1,Ⅲ区坝基弹性模量按Er/Ec=0.1、0.2…1、1.2、1.5、2、2.5、3、3.5、4 改变;④方案四:Ⅰ、Ⅱ、Ⅲ三块区域作为一个整体,同时按Er/Ec=0.1、0.2…1、1.2、1.5、2、2.5、3、3.5、4 改变。计算时坝体混凝土的重度和泊松比分别取为24 kN/m3和0.2,坝基岩体的泊松比均取为0.32。
本文采用有限元法分析广源水电站坝基弹性模量对拱坝动力特性的影响,具体分析采用ANSYS软件实现。
根据拱坝坝高和坝址的地形地质条件,确定有限元计算的模拟范围为:基岩底部高程取286 m,从拱坝左右坝肩分别向左右两岸各取125 m,顺河流向从坝轴线向上游取170 m,从坝轴线向下游取260 m,坝基有限元模型按照实际地形建立。
整体坐标系为X 向右岸为正,Y 向下游为正,Z向上为正的笛卡尔坐标系。应力、位移符号与弹性力学规定一致,即拉为正,压为负。模型底部坝基为固端约束,其他侧面为单向链杆约束。有限元模型采用SOLID185 高阶3D8 节点实体单元,坝体单元数为8091 个,节点数为8349 个,坝基单元数为135 544 个,节点数为78 641 个。有限元计算模型见图1。

图1 有限元计算模型
为减少由于坝基质量而造成的加速度放大的现象,且同时考虑坝基刚度对拱坝动力响应的影响,动力计算模型采用无质量坝基模型,根据附加水体质量法的原理,在ANSYS 中通过施加MASS21 单元来实现动水压力的施加,计算水位为正常蓄水位478 m,坝体施加附加水体质量单元前后如图2所示。
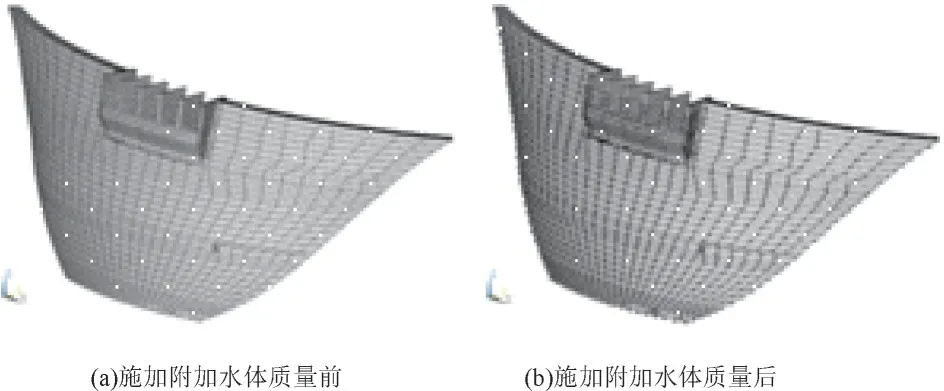
图2 施加附加水体质量前后对比图
1.4 参数选取
计算采用的静力参数见表1。根据现行《中国地震动参数区划图》(GB18306-2015),本工程地震动峰值加速度值为0.05 g,相应的地震烈度为Ⅵ度,场地类别为Ⅱ类场地,根据《水电工程水工建筑物抗震设计规范》(NB 35047-2015),场地特征周期为Tg=0.35 s,对于拱坝设计反应谱最大值的代表值取βmax=2.5,最后确定设计反应谱如图3所示,设计反应谱表达式为:
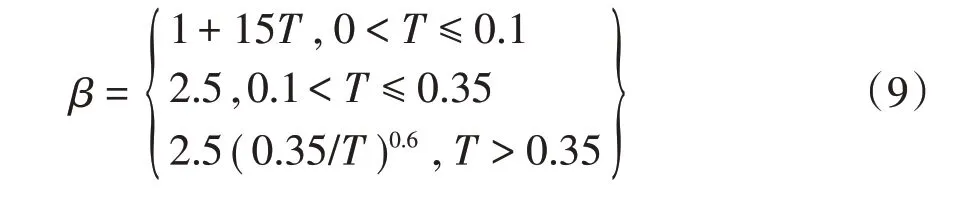
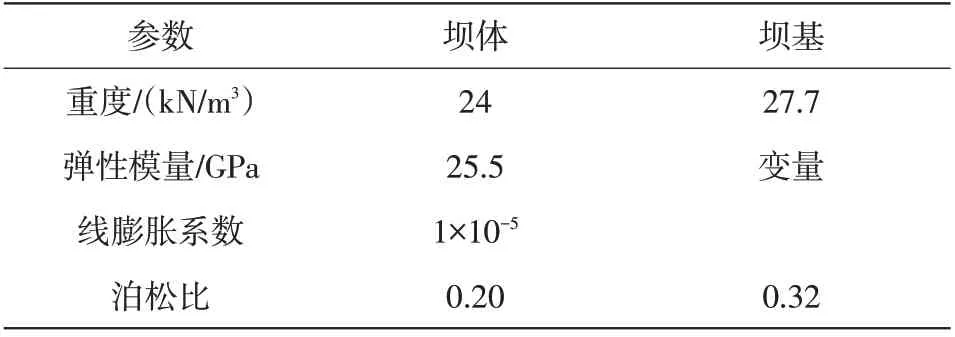
表1 坝体及坝基材料参数
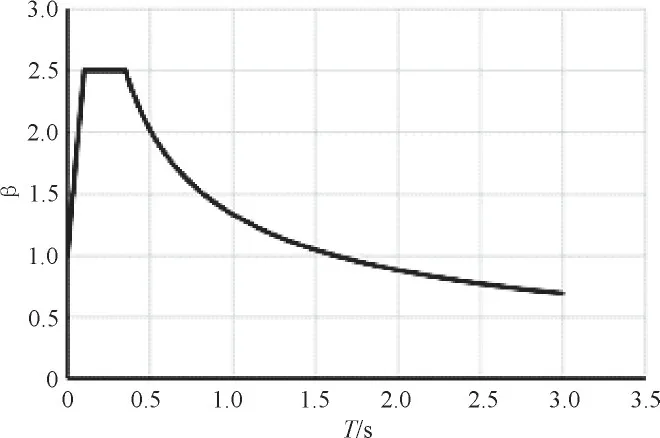
图3 设计反应谱
根据现行抗震规范的相关规定,对不进行专门的试验确定其混凝土材料动态性能的大体积水工混凝土建筑物,其混凝土动态强度的标准值可较其静态标准值提高20%,相应的材料性能分项系数可取1.5;其动态弹性模量标准值可较其静态标准值提高50%;其动态抗拉强度的标准值可取为其动态抗压强度标准值的10%。在混凝土水工建筑物的抗震稳定计算中,坝基岩体的动态变形模量可取其静态变形模量[5]。因此,本文对坝基弹性模量仍按照与静态混凝土弹性模量比值计算的结果取值,而对于坝体混凝土,其动态弹性模量取为静态的1.5倍。
2 坝体自振特性影响分析
2.1 坝体振型分析
为了分析坝基弹性模量对坝体振型的影响,采用振型分解反应谱法对方案一~方案四的各种弹性模量组合进行了计算分析,其中Er/Ec=0.1和Er/Ec=1的前四阶振型图,分别见图4~图8。
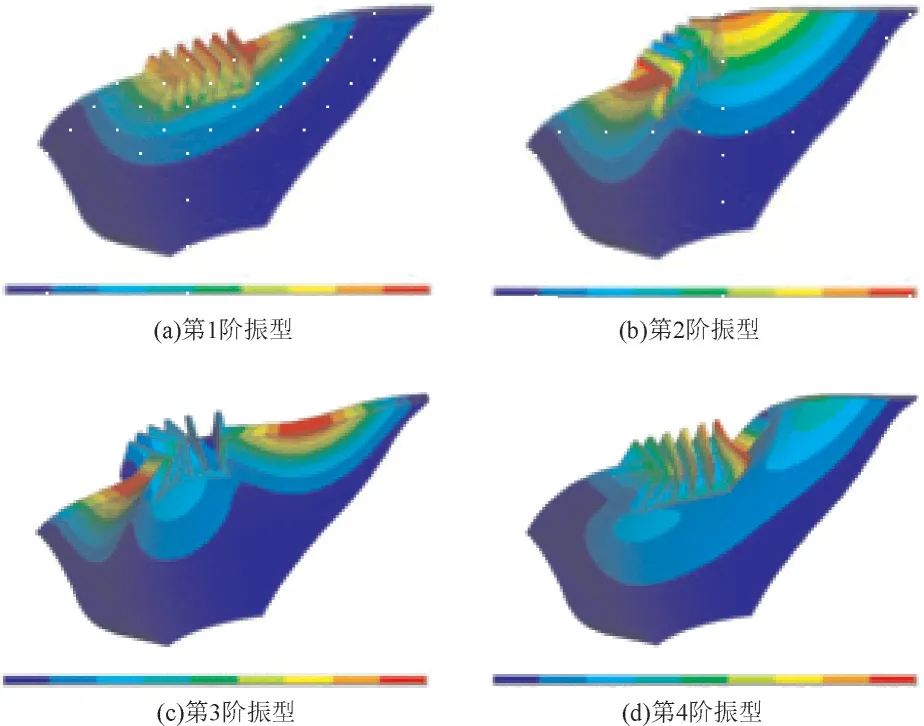
图4 方案一Er/Ec=0.1前四阶振型图
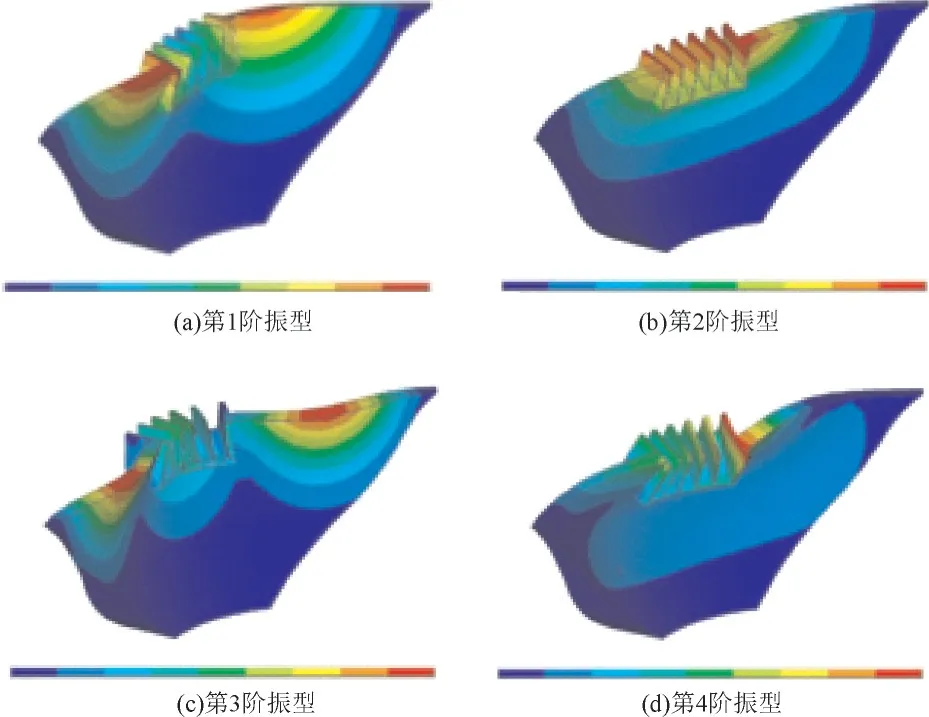
图5 方案二Er/Ec=0.1前四阶振型图
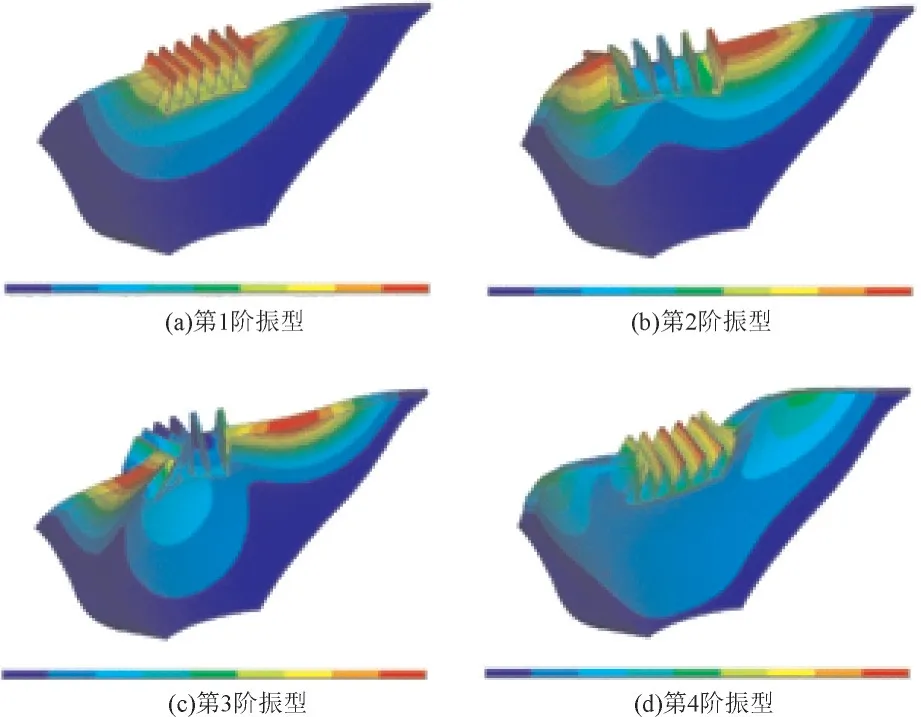
图6 方案三Er/Ec=0.1前四阶振型图
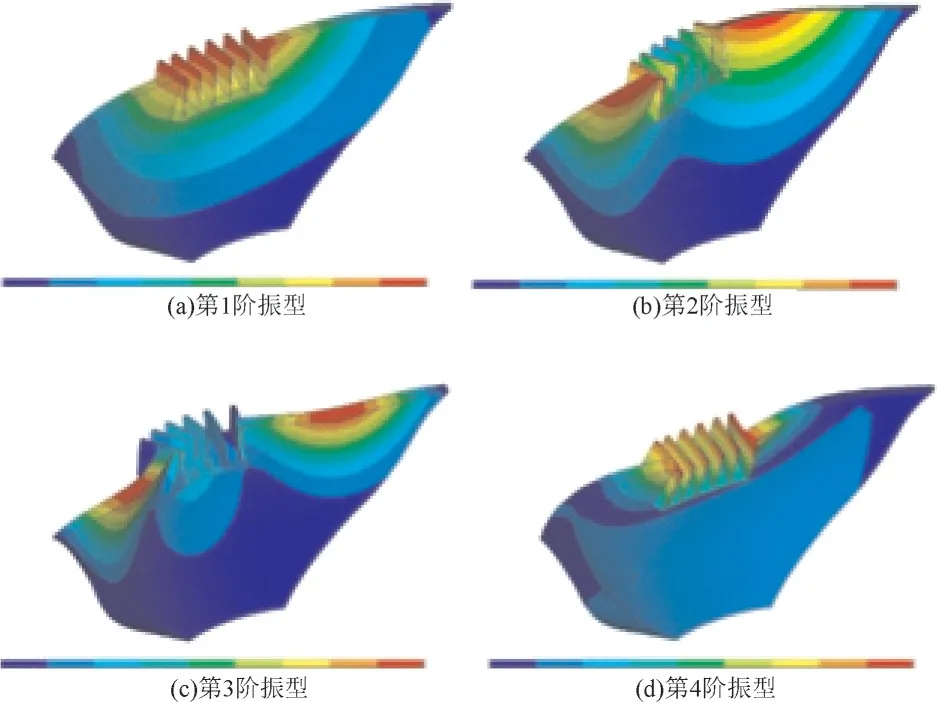
图7 方案四Er/Ec=0.1前四阶振型图
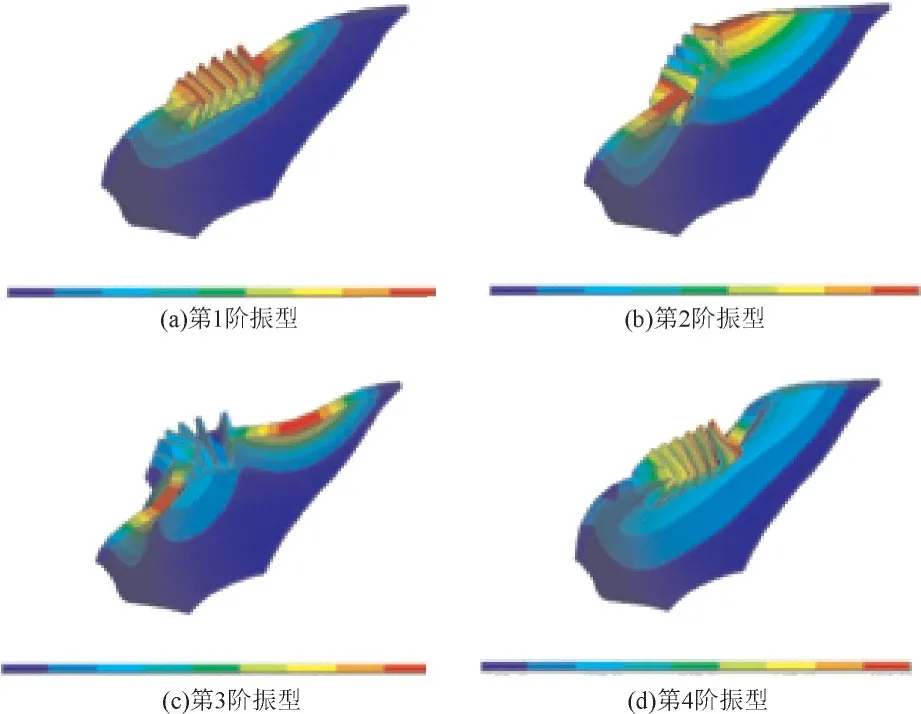
图8 Er/Ec=1前四阶振型图
坝体振型的计算结果表明:Ⅰ区和Ⅲ区坝基的弹性模量变化对坝体振型的影响不大,第一振型均为对称,第二振型为反对称;Ⅱ区坝基弹性模量对坝体的振型有较大影响,当Ⅱ区坝基Er/Ec<0.3时,第一振型为反对称;第二振型为对称,Er/Ec>0.3后,第一振型为对称振型,第二振型为反对称。
2.2 自振频率分析
4个坝基弹性模量组合方案Er/Ec=0.1、0.5、1、2时的自振频率曲线见图9,由图可知,当Er/Ec=0.1时,各方案曲线变化趋势大致一样,只是数值差异,且前3 个方案与方案四对比容易发现,方案二比较接近方案四曲线,依次到方案三,再到方案一,这说明中部区域的坝基对坝体自振频率影响最大,下部区域次之,上部影响最小。另外还可以发现,各阶振型随着Er/Ec越大,各方案曲线逐渐趋于重叠,当Er/Ec=0.5时,曲线已经基本重合。
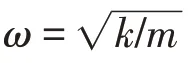
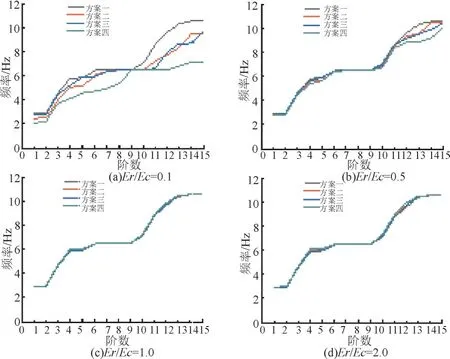
图9 各方案频率曲线
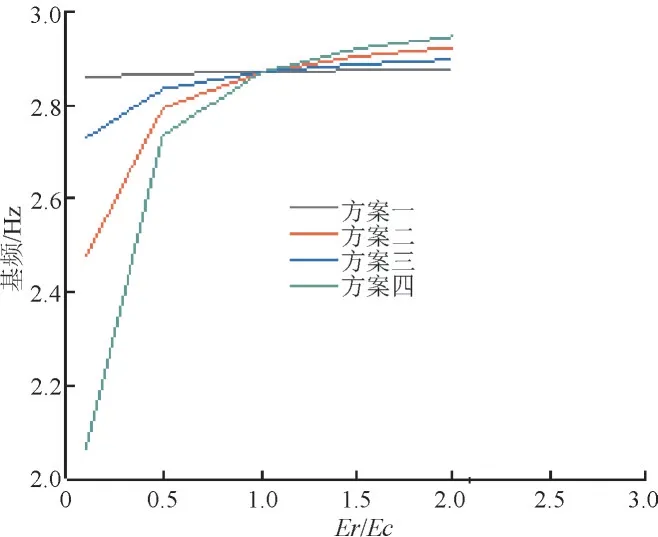
图10 各方案基频曲线
3 反应谱动力响应分析
本文利用振型分解反应谱法[6]原理编写命令流,计算拱坝在地震作用下的动力响应。反应谱采用现行规范推荐的设计反应谱(见图3),最大谱值取β max=2.5,阻尼比取5%。根据计算出的各振型地震作用效应,对模态扩展后采用平方和方根即“SRSS”方法进行模态组合,考虑顺河向、横河向和竖向地震的同时作用。
3.1 位移结果分析
为研究坝基弹性模量对拱坝在反应谱分析中的整体位移分布规律,对4 个方案中坝基弹性模量为Er/Ec=0.1及整体坝基弹性模量Er/Ec=1五种情况下的位移进行对比分析,5 种情况下地震产生的各向最大位移值见表2。由此得出以下结论:
顺河向位移:坝基弹性模量越小,最大顺河向位移值越大,而从Ⅰ区、Ⅱ区和Ⅲ区坝基来对比,Ⅱ区坝基弹性模量影响程度较大,Ⅲ区坝基次之,Ⅰ区影响最小。
横河向位移:整体坝基弹性模量较为一致时能有效降低坝体最大横河向位移,当中部(Ⅱ区)较上部(Ⅰ区)和下部(Ⅲ区)坝基的弹性模量小时,最大横河向位移会增大。
竖向位移数值均较小,对竖向位移而言,各区域坝基影响程度为:Ⅲ区坝基>Ⅱ区坝基>Ⅰ区坝基。
总位移:五种情况下的总位移分布规律大体一致,表明坝基弹性模量对拱坝动位移的影响主要还是表现在对数值的影响上,总的来说,坝基弹性模量越小,总位移越大。
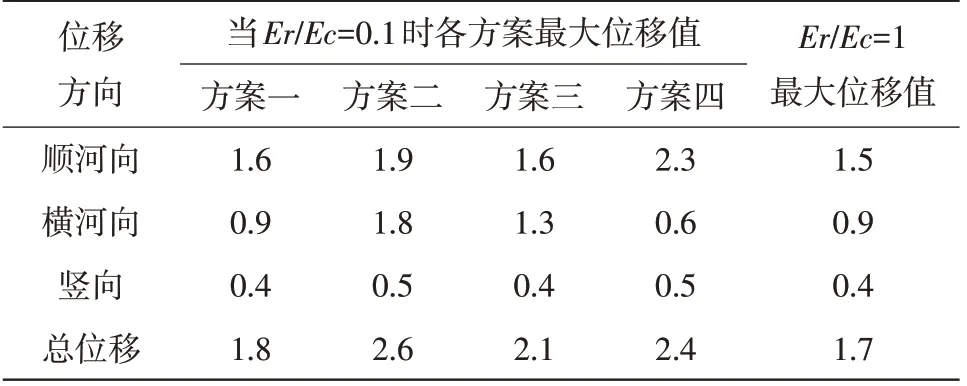
表2 五种情况下地震产生的各向最大位移值 cm
3.2 应力结果分析
计算结果表明,各方案之间应力分布规律大体相同,坝基弹性模量对坝体动力下应力分布规律也没有本质的影响,仅是数值上有所差异。
方案一中Er/Ec=0.1时最大拉应力为5.63 MPa;方案二中Er/Ec=0.1 时最大拉应力为5.9 MPa;方案三中Er/Ec=0.1 时最大拉应力为5.7 MPa;方案四中Er/Ec=0.1 时最大拉应力为6.21 MPa;当Er/Ec=1 时最大拉应力为5.44 MPa。从坝基弹性模量大小来分析,坝基弹性模量越小,动应力水平越大,而且影响程度依次为:Ⅱ区坝基>Ⅲ区坝基>Ⅰ区坝基。
4 地震时程法分析
4.1 地震波的选取
拱坝进行动力时程分析时,将地震波作为地震荷载直接输入,广源水电站工程坝址区在历史上并未有过强震和完整地震动记录,工程场地类别属Ⅱ类场地,依据现行《水电工程水工建筑物抗震设计规范》(NB35047-2015),场地特征周期为Tg=0.35 s,设计反应谱最大值的代表值取2.5,本文根据设计反应谱拟合了人工波加速度时程曲线,加速度峰值为1 m/s2,时间间隔为0.02 s,加载步数为750 步,地震持时15 s,在动力响应中的结构质量阻尼α 和刚度阻尼β利用下式计算[7]:
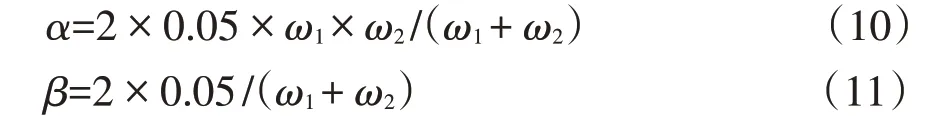
4.2 位移结果分析
地震作用时拱坝主要是发生顺河向和横河向位移的震荡,计算结果表明,广源水电站拱坝坝基弹性模量的变化对顺河向和横河向位移的影响的规律是相似的,限于本文的篇幅,只对顺河向地震位移时程进行分析,并以拱冠梁顶点作为特征点。从拱冠梁顶点处顺河向位移时程曲线(见图11)看,(a)和(e)位移时程大致一致,说明上部坝基弹性模量对坝体最大顺河向位移时程影响不大,而中部和下部坝基弹性模量对坝体最大顺河向位移时程都有显著影响。从振幅衰减期上看,(b)<(c)<(e)<(d),表明整体坝基弹性模量大致一致的时候,衰减期较短,且整体坝基弹性模量越小,衰减期越短。从峰值上看,4 种方案峰值大致相等,均在6 cm 左右。
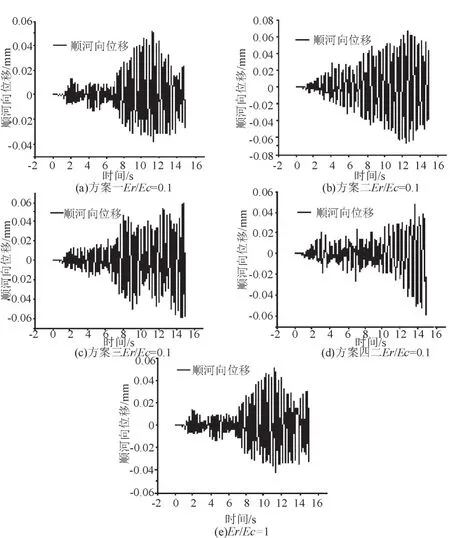
图11 各方案顺河向位移时程曲线
4.3 应力结果分析
计算结果表明,对于坝体应力时程,坝体上部拱端和拱冠梁底部的动应力时程受到坝基弹性模量的影响比较大。坝基的均匀性对坝体的动力响应影响较大,坝基各部位弹性模量基本一致,特别是中部和下部坝基弹性模量一致时,动应力时程峰值比较小,此时衰减期也较长,中部坝基和下部坝基弹性模量差异较大时,会导致动应力时程峰值增大,且衰减期较短,坝体动应力状态比较复杂,对坝体不利。
5 结论
(1)通过自振频率分析发现,当Er/Ec<0.5时,各区域坝基弹性模量对拱坝自振频率影响较大,坝基弹性模量越大,坝体自振频率越大,当Er/Ec≥0.5,坝体自振频率基本不受坝基弹性模量的影响。
(2)对于振型,中部坝基影响最大,当Ⅱ区坝基Er/Ec<0.3时,坝体第一振型表现为反对称振型,其他情况第一振型均表现为对称振型。坝基各部位的弹性模量对地震时坝体的位移和应力均有较大影响,影响主要表现在数值上,坝基弹性模量越大,动位移和动应力越小,各部位的影响程度为:中部>下部>上部。
(3)由反应谱动力响应分析可知:4 种方案的位移和应力分布规律大体一致,表明坝基弹性模量对拱坝动位移的影响主要还是表现数值上,坝基弹性模量越小,总位移越大。
(4)通过动力时程分析可知,坝基各部位的弹性模量对坝体上部拱端和拱冠梁底部的动应力影响较大;坝基的均匀性对坝体的动力响应影响较大,当坝基各部位尤其是中、下部坝基弹性模量一致时,动应力时程峰值较小,衰减期较长,反之则会导致动应力时程峰值过大,且衰减期较短。
