用于样本聚类和网络分析的整合鲁棒结构化NMF模型
2020-10-21张晓宁孔祥真罗传文刘金星
张晓宁,孔祥真,罗传文,刘金星
1.曲阜师范大学计算机学院,山东日照276826
2.北京林业大学信息学院,北京100083
癌症一直是全世界尚未攻克的难题,它对人类健康构成严重威胁.随着科技的发展,人类已经初步揭开了它的神秘面纱,但对于其内在机制和发病机理仍知之甚少.因此,对癌症数据进行深入研究是十分有必要的.但是癌症数据通常具有高维度小样本的特性,且可能存在大量的噪声和异常值[1],这可能会给癌症数据的研究带来不良影响.
为此,Lee 和Seung[2]于1999年提出非负矩阵分解(non-negative matrix factorization,NMF)算法.这是一种有效的数据降维方法,可以通过把高维数据映射到低维空间来获取高维数据的低维表示.该方法因具有非负性和较好的可解释性[3],而被广泛应用于图像处理、文本识别和生物信息学等领域.随后,研究人员不断对NMF 方法进行改进并提出了许多的变体方法.为了增强算法的稀疏性,Hoyer等[4]在两个分解因子上分别施加了L1范数约束,进而提出了稀疏约束NMF(NMF with sparseness constraints,NMFSC)方法.基于普通图理论,Cai等[5]提出了图正则NMF(graph-regularized NMF,GNMF)方法,该方法保留了数据空间的内部几何结构.Wang等[6]在目标函数中施加了L2,1范数约束来减弱噪声和异常值的影响,从而提高了算法的鲁棒性.为了更好地保留数据之间的高阶几何关系,Zeng等[7]提出了超图正则化非负矩阵分解(hypergraph regularized non-negative matrix factorization,HNMF)算法.
随着高通量测序技术的发展,多组学数据的大量涌现为从系统层面研究癌症的发病机制提供了机遇.单一的NMF 模型不能同时处理多种类型的数据,为此,Zhang等[8]提出联合NMF(joint NMF,jNMF)模型并将其用于处理多种类型的基因组学数据.该方法可以较好地鉴别特征基因,它的提出为从系统层面揭示基因调控机制提供了新的思路.随着整合模型的开发,如何处理不同类型数据中的异质性成为研究的重点.为了增强整合模型的异构效应,Yang等[9]在jNMF 方法的基础上施加了一个惩罚项,提出了整合NMF(integrative NMF,iNMF)方法.利用该方法来处理多种类型的基因组数据,可以挖掘癌症相关途径和亚型之间的通用模块.作为jNMF 的扩展方法,iNMF 不仅能够有效整合多类型数据的潜在公共信息,而且能灵活地处理数据之间的异构性.在后来的研究中,Stražar等[10]施加正交约束,提出了整合正交化的NMF(integrative orthogonality-regularized NMF,iONMF)方法,提高了整合模型的分类能力.该方法对多个数据源进行整合并实现了RNA 结合模式的预测.可以确定的是,iONMF 是一个稀疏模块化的整合模型.考虑到数据之间的内在几何结构,Gao等[11]提出了整合的超图正则化NMF(integrated graph-regularized NMF,iGNMF)模型.该模型可以保留原始数据中的内部几何结构,从而保留数据之间的异质性[12].此外,利用该模型构建基因共表达网络能够更好地挖掘基因之间的关联和癌症信息.
尽管上述整合模型取得了较好的应用效果,但模型的同质效应和鲁棒性仍有待提高.为此,本文提出了整合鲁棒结构化NMF(integrated robust structured NMF,iRSNMF)模型.该模型是一个整合模型,能够实现多种类型数据的集成.利用整合模型处理多种类型的癌症数据,一方面可以挖掘不同类型数据之间的潜在关联,另一方面还可以提取癌症数据的全局特征.这有利于从系统层面探索癌症的发病机制,进而为癌症的治疗提供依据.为了提高算法的同质效应,iRSNMF 模型引入了一个结构化项,通过最小化基矩阵之间的差异来更好地保留不同类型数据之间的同质性.此外,为了提高算法的鲁棒性,在该模型中施加了L2,1范数约束,这可以减小冗余特征的影响.构建基因共表达网络是展现基因间相互作用关系的一种有效手段,能够在系统层面反映基因间的关联,有助于研究人员掌握基因在癌症中的作用及其生物功能.为了验证该方法的可行性和有效性,本文将其应用于癌症样本聚类实验和基因共表达网络分析.
1 相关工作
1.1 联合NMF 算法
jNMF 是一个经典的整合模型,能够实现不同类型数据的集成[8].该方法将不同类型的基因组数据映射到一个公共低维空间中,进而获取同一方向上的多维模块.位于同一模块的特征可能具有很强的相关性或潜在关联[8].在生物信息学领域中,癌症数据可以用矩阵表示.假设给定d个不同类型的数据,分别用非负矩阵Xi ∈Rm×n,i=1,2,···,d表示.jNMF 的目标是将Xi分解为一个公共基矩阵U ∈Rm×k和每个类型独有的系数矩阵Vi ∈Rk×n,使U和Vi的乘积无限近似于原始数据Xi.jNMF 的模型如下:

式中,公共基矩阵U可以保留不同类型的数据之间的共享信息.jNMF更新规则如下:
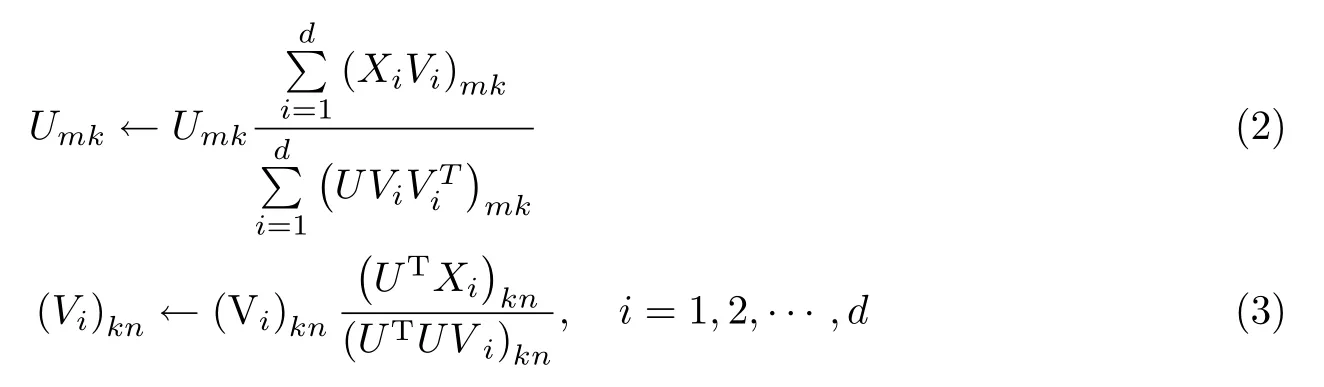
作为NMF 的扩展模型,jNMF 在保留NMF 的非负和易解释的特性的同时,还可以有效整合多种类型数据之间的潜在公共信息[12].利用该模型可以捕获位于高维基因组数据中的模块化结构.而通过挖掘这些模块可以为揭示癌症的分子机制提供思路.
1.2 结构化的低秩矩阵分解表示算法
随着多组学数据的发展,多视图聚类研究引起了学者的广泛关注.在多视图聚类的研究中通常会持有一个合理的假设,那就是所有的视图的基础聚类结构应该是相似的[13].因此,Wang等[13]提出了一个结构化低秩矩阵分解算法.该算法的目标函数如下:
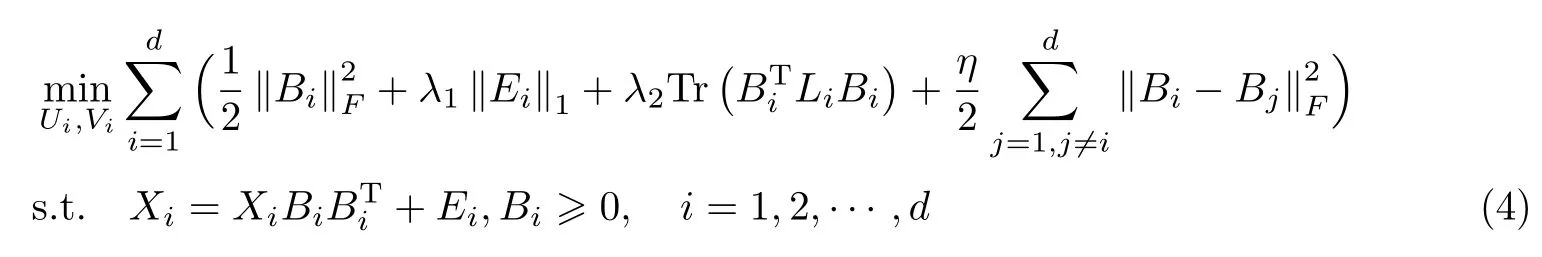
式中,Bi为第i个视图Xi的分解低秩数据集群表示,Ei为第i个视图的噪声数据,Li为第i个视图的图拉普拉斯矩阵,λ1、λ2、η均为平衡参数.该算法引入了一个图正则化项,它可以更好地保留原始数据的局部流形结构.在原始数据的低维表示上施加图正则化器能够更好地适应多视图光谱聚类,从而提高聚类性能.此外,为了获得更加相似的基础聚类结构,Wang等[13]在函数中引入了一个结构化项,从而在分解过程中最小化不同视图之间的差异.
2 整合鲁棒结构化NMF 算法
2.1 模型创建
iRSNMF 是传统NMF 的扩展模型,因此它保留了NMF 方法的非负和易解释的特性.该模型可以集成不同类型的数据,这有利于保留数据之间的潜在公共信息.为了提高整合模型的同质效应,iRSNMF 模型引入了一个结构化项.它可以最小化因式分解中基矩阵的差异以更好地保留不同类型数据之间的同质性.此外,通过对分解后的公共系数矩阵施加L2,1范数约束可以提高算法的鲁棒性.该模型的目标是将d种类型的数据Xi ∈Rm×n,i=1,2,···,d分解为d个基矩阵Ui ∈Rm×k和一个公共系数矩阵V ∈Rk×n,使二者的乘积近似于原始数据矩阵.iRSNMF 的目标公式如下:

式中,λ≥0 和β≥0 分别为平衡结构化项和V稀疏程度的参数.G为对角矩阵,第j个对角元素值定义如下:
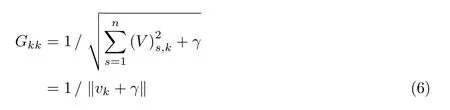
式中,γ是一个无限接近于0 但不等于0 的正数.
2.2 模型优化
本节采用乘法更新规则来迭代更新目标函数.根据式(5),拉格朗日函数定义如下:
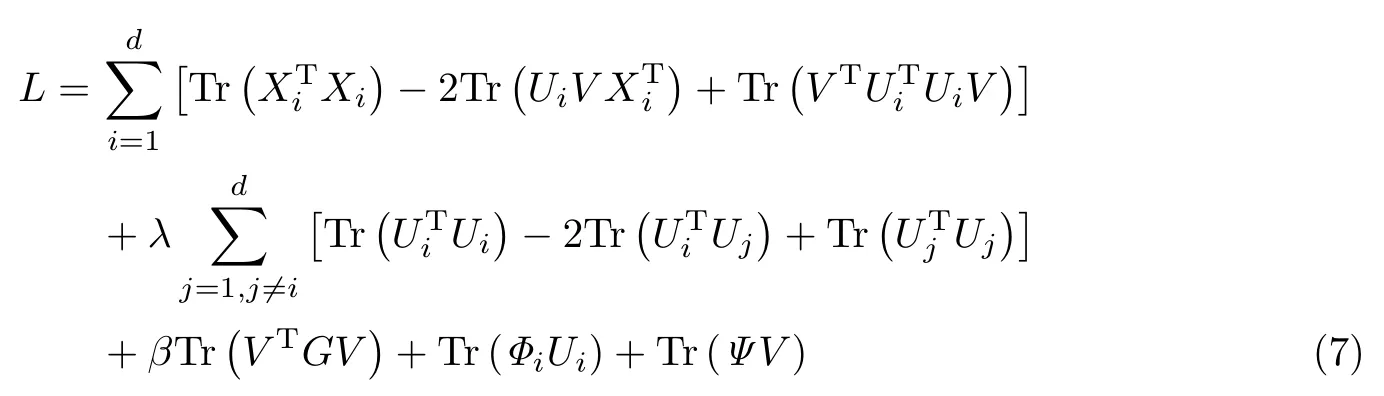
式中,Φi=[(ϕi)mk]和表示控制Ui0 和V≥0 的拉格朗日乘子.
然后,对Ui和V分别求偏导,可得

根据Karush-Kuhn-Tucher(KKT)条件(ϕi)mk(ui)mk=0 和ψknvkn=0,得到如下更新公式:

算法1 中给出了iRSNMF 的完整步骤,该算法会不断迭代直到算法收敛.
算法1iRSNMF
输入:Xi ∈Rm×n
输出:Ui ∈Rm×k,V ∈Rk×n
初始化:Ui≥0,V≥0
设置迭代次数r=1
循环
通过式(10)更新Ui;
通过式(11)更新V;
本项目污水处理厂服务区域面积为23.4平方公里,工程规划设计规模为10万m3/d,其中一期已建规模4.8万m3/d,尾水排放标准按照 《城镇污水处理厂污染物排放标准》(GB18918-2002)二级标准执行。工程占地面积120.6亩,于2007年开始动工建设,目前该厂正式投入运行。
r=r+1;
直至收敛
2.3 收敛性与运行时间分析
本节给出了iRSNMF 算法的收敛性和运行时间分析.本文采用乘法迭代更新规则优化算法.通过乘法迭代更新规则,目标的误差函数值将会不断减小直到误差值无限趋近于0 或者达到最大迭代次数算法才会停止,从而确保算法的收敛性.本节绘制了5 个整合方法的收敛曲线,如图1所示.其中x轴表示迭代次数,y轴表示误差值.从图1中可以看出,随着迭代次数的增加,这5 种方法的误差逐渐减小,且均在第100 次迭代时趋于收敛.其中,jNMF、iGNMF、iRSNMF 这3 种方法的收敛曲线近似,但iNMF 和iONMF 的初始误差比较大.
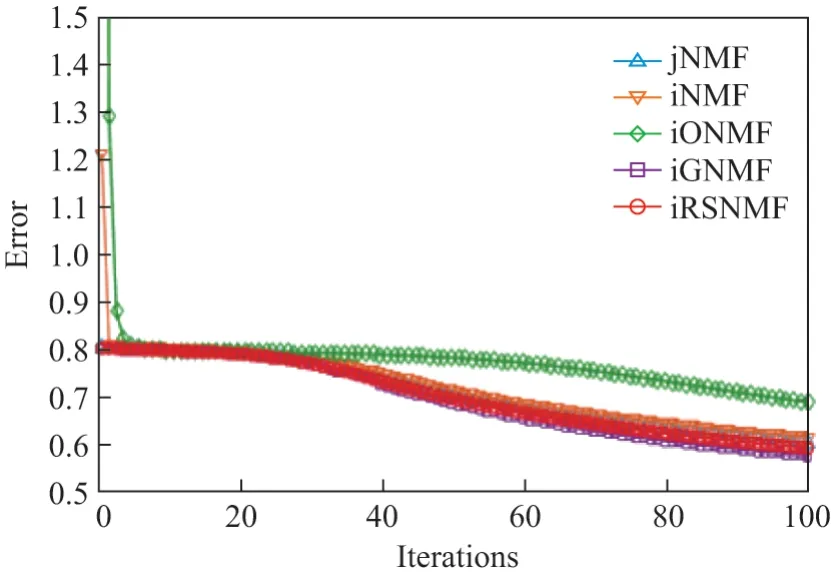
图1 不同方法的收敛曲线Figure 1 Convergence curves of different methods
为公平起见,在分析算法的运行时间时,所有方法都运行50 次并计算其均值,结果如表1所示.由表1可知,SVD 和PCA 的运行时间特别短,是因为这两个方法均无需迭代.iNMF 和iONMF 运行所需的时间较长,是因为iNMF 目标函数中包含了一个异构效应惩罚项,而iONMF 的目标函数中包含了一个正交约束,所以它们的时间复杂度更高.

表1 不同方法的运行时间Table 1 Running time of different methods s
3 实验及结果分析
本节在整合数据集上进行样本聚类和构建基因共表达网络的实验,并对实验结果加以分析.奇异值分解(singular value decomposition,SVD)算法和主成分分析(principal component analysis,PCA)算法作为经典的降维算法,被广泛应用于图像处理和机器学习等领域.SVD 方法可以直接分解原始数据矩阵以获取能够代表原始数据的低维矩阵,进而达到降维的目的.PCA 方法可以通过线性变换来提取原始数据的主要特征,从而实现降维.SVD 和PCA 通过去除原始数据中的噪声和冗余信息来达到优化数据,提高实验性能的目的.SVD 和PCA 两种方法只能用于处理单一类型的数据,无法同时处理多种数据类型.因此,在聚类实验部分,我们采用SVD 和PCA 分别在GE、ME、CNV 3 种数据类型上进行聚类实验并取其均值作为最终的聚类结果.聚类结果如表3∼6 所示.
在样本聚类实验部分,将iRSNMF 模型与SVD、PCA 及其他整合模型(jNMF、iNMF、iONMF、iGNMF)的聚类性能进行对比.具体地,对于SVD,利用其分解后的右奇异值矩阵进行聚类;对于其他整合模型,利用其分解后的系数矩阵进行聚类.上述方法均采用K-means 算法进行聚类实验.在聚类实验中,所有方法都执行50 次并取均值作为最终聚类结果.为了进一步验证新模型的有效性,在网络构建部分分别在Cytoscape 软件上利用5 个整合模型进行构网以筛选重要基因并将筛选结果进行比较.最后,利用iRSNMF 模型构建基因共表达网络,对网络中的重要基因和通路进行分析并给出它们的相关生物学解释.
3.1 数据集
本文将胰腺癌(pancreatic adenocarcinoma,PAAD)、食管癌(esophagealcarcinoma,ESCA)、头颈麟癌(head and neck squamous cell carcinoma,HNSC)和结直肠癌(colon adenocarcinoma,COAD)4 个数据集中任意3 个进行整合,从而获得PAAD_ESCA_HNSC(PEH)、PAAD_ESCA_COAD(PEC)、PAAD_HNSC_COAD(PHC)和ESCA_HNSC_COAD(EHC)4 个数据集.每种癌症的原始数据可从TCGA(https://tcgadata.nci.nih.gov/tcga/)下载得到.最终的整合数据集均包含3 种数据类型,即基因表达(gene expression,GE)、甲基化(methylation,ME)、拷贝数变异(copy number variation,CNV).在数据预处理部分,首先对整合数据集进行降维以摒除冗余信息,然后将处理后的数据归一化.具体的数据集信息如表2所示.
3.2 评价指标
本文采用精确度(accuracy,ACC)、调整兰德系数(adjusted rand index,ARI)、归一化互信息(normalized mutual information,NMI)、召回率(Recall)、准确率(Precision)、F 值(Fmeasure)[14-15]6 个常用指标来度量上述5 种整合方法的聚类性能.它们的值越大,说明该方法的聚类性能越好.

表2 整合数据集的详细信息Table 2 Details of the integrated dataset
假设H={H1,H2,···,HN}和L={L1,L2,···,LN}分别表示真实的聚类集和预测得到的聚类集.ACC表示样本被正确聚类的比例,定义如下:
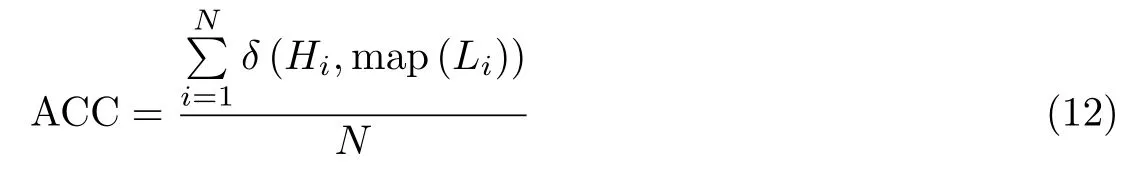
式中,N为总的样本个数,Hi和Li分别表示真实标签和聚类得到的预测标签.map(·)是将预测标签映射到真实标签的函数.若x=y,则函数δ(x,y)值为1,否则为0.
ARI 是用于衡量这两个数据分布的吻合程度的量度.ARI 的定义为

式中,Nij为Hi和Lj中同时存在的样本个数,Ni.和N.j分别表示Hi和Lj中的样本个数.
NMI 表示两个聚类集合的相似性,互信息(MI)可表示为
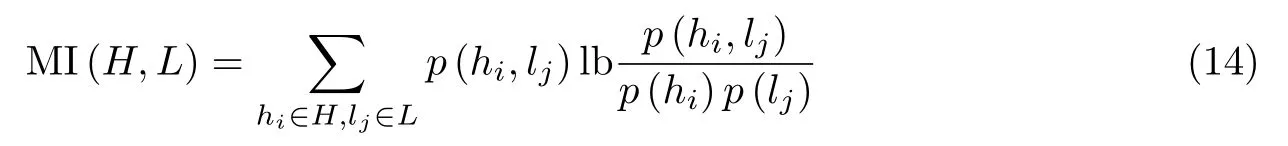
式中,p(hi)和p(lj)分别表示某一样本属于H和L的概率.p(hi,lj)是样本同时属于H和L的概率.NMI 的定义为
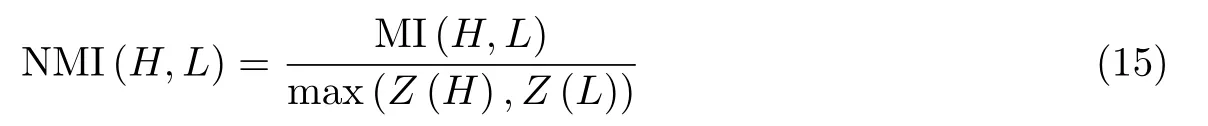
式中,Z(H)和Z(L)分别是H和L的熵.
Recall、Precision、F-Measure 也是常用的聚类评价指标,它们的定义如下:

式中,T1表示来自同一聚类集的两个样本被划分在同一聚类集.F1和F2分别为将两个来自不同聚类集的样本划分为同一聚类集和不同聚类集.
3.3 参数选择
在聚类实验中,SVD 和PCA 没有需要设置的超参数.实验中涉及到的整合模型都需要对矩阵分解维度k进行选参.由于参数k的取值应远小于原始矩阵的维度,并且在实验过程中当k的取值大于100 时聚类性能相对平稳,因此将参数k的选参区间设置为[2,100].不同方法对应参数k的不同取值在4 个数据集上的影响如图3所示.从图3中可以看出,在4 个数据集上,当k的取值分别为40、7、8、5 时,jNMF 的聚类性能最好.当k的取值分别为30、4、8、8 时,iNMF 的聚类性能最好.当k的取值分别为70、8、6、8 时,iONMF 的聚类性能最好.当k的取值分别为70、3、8、5 时,iGNMF 的聚类性能最好.当k的取值分别为50、8、7、7 时,iRSNMF 的聚类性能最好.
iRSNMF 模型还需要对λ、β进行选参.我们利用网格搜索算法来选择最优参,参数λ和β的取值区间分别为λ和β的不同取值在4 个数据集上的影响如图2所示.从图2可以看出,合适的取值可以取得好的聚类结果.当参数λ和β的取值分别为时,iRSNMF 能取得较好的聚类精确度.为公平起见,我们同样为对比方法选择了最优参进行实验.iNMF 方法需要设置超参数µ用于平衡数据中的同质性(或异质性)程度,取值为1 000.iONMF 方法需要设置超参数α用于控制系数矩阵中列向量的正交性,取值为0.01.iGNMF 方法需要设置超参数δ用于调整方程的平滑度,取值为0.01.

图2 参数λ 和β 的不同取值在4 个整合数据集上的影响Figure 2 Influence of different values of the parameters λ and β on the four integrated datasets
3.4 聚类及结果分析
矩阵分解时的随机初始化会使聚类性能不稳定.为了尽可能消除这一不利影响,在聚类实验中,所有方法都执行50 次.不同方法在4 个数据集上的聚类性能如表3∼6 所示.
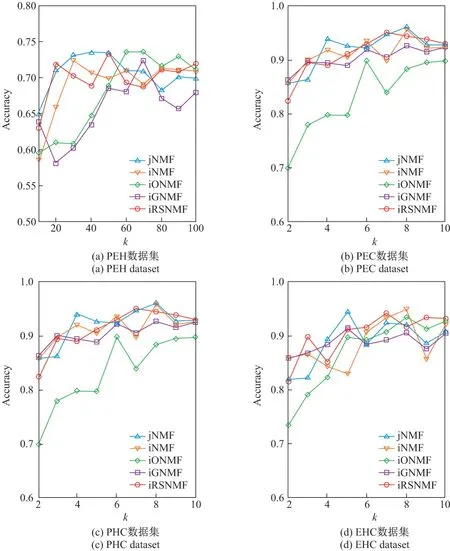
图3 参数k 的不同取值在4 个数据集上的影响Figure 3 Influence of different values of parameter k on the four datasets
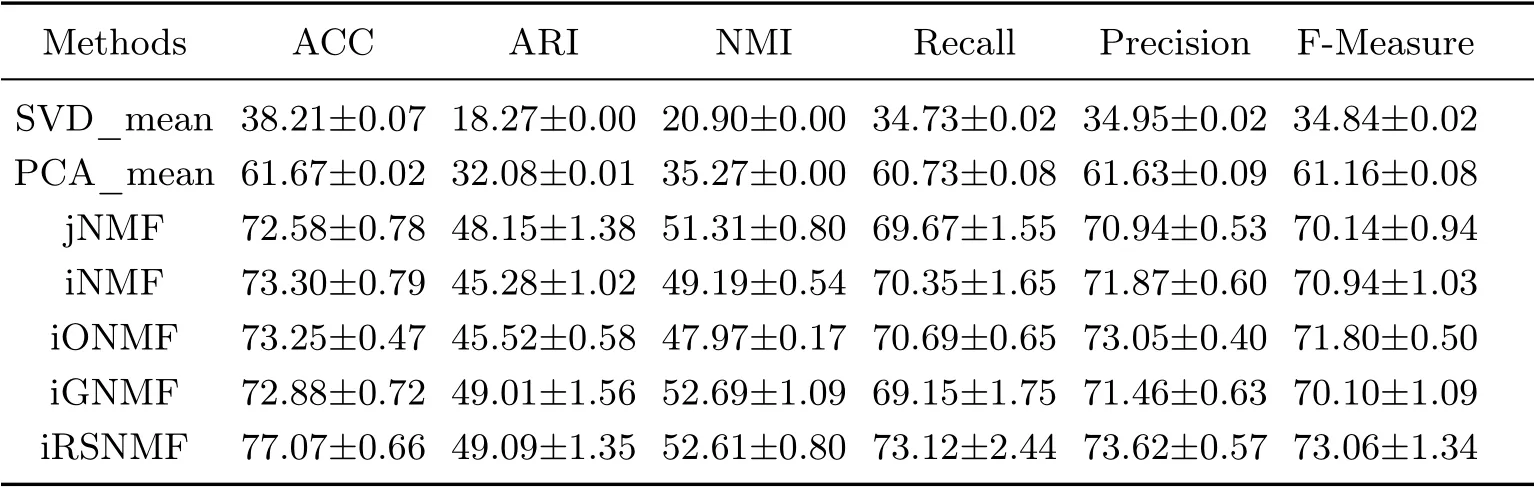
表3 不同方法在PEH 数据集上的聚类性能比较Table 3 Comparison of clustering performance of different methods on PEH dataset
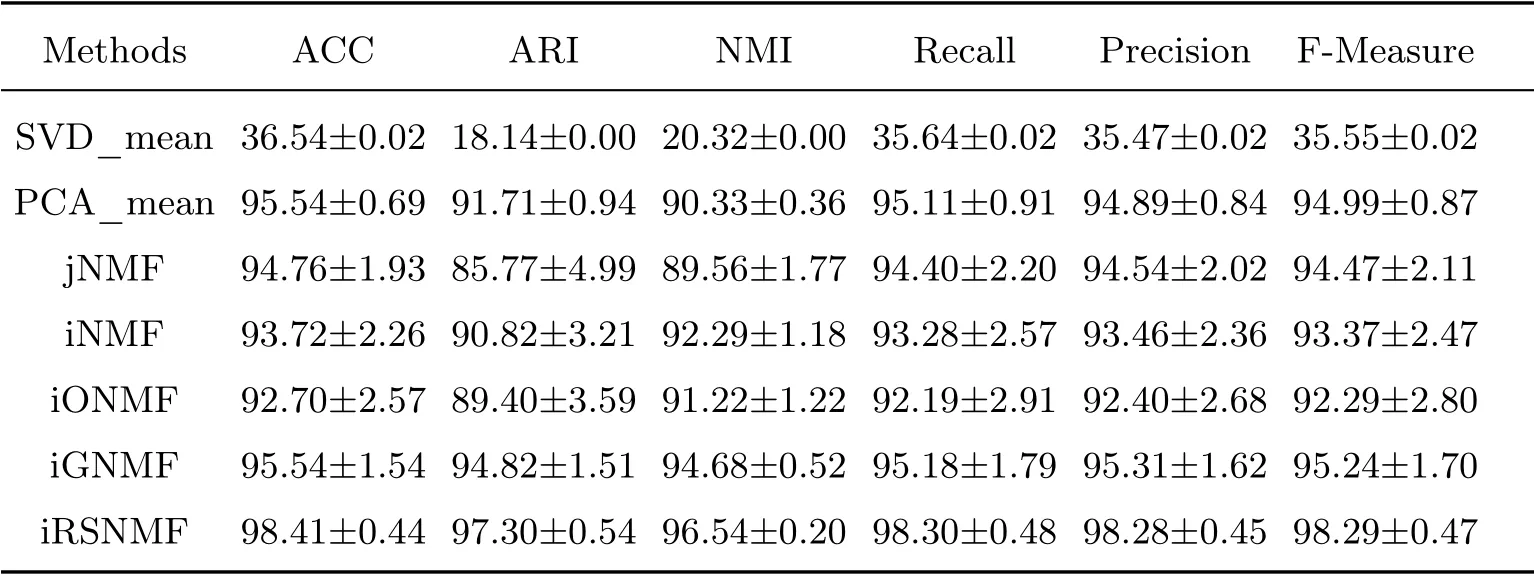
表4 不同方法在PEC 数据集上的聚类性能比较Table 4 Comparison of clustering performance of different methods on PEC dataset
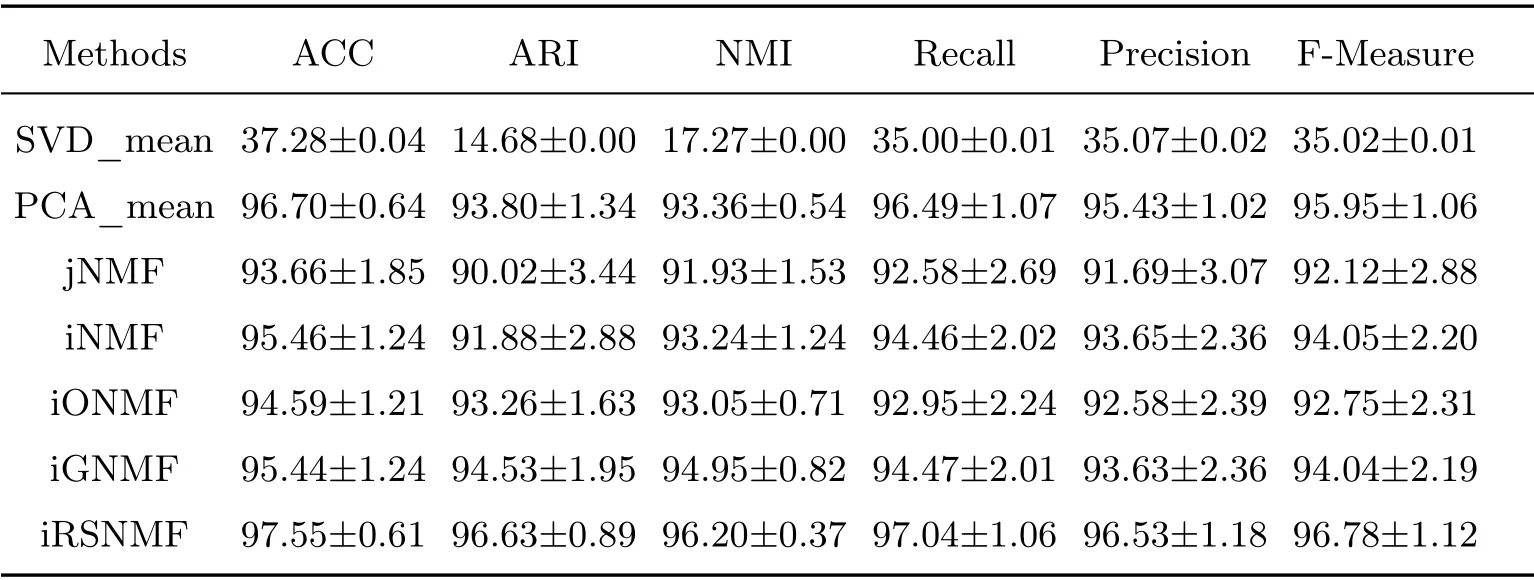
表5 不同方法在PHC 数据集上的聚类性能比较Table 5 Comparison of clustering performance of different methods on PHC dataset

表6 不同方法在EHC 数据集上的聚类性能比较Table 6 Comparison of clustering performance of different methods on EHC dataset
根据表3∼6 可以得出以下结论:
1)总体来看,在ACC、ARI、NMI 上,jNMF 的平均值比PCA_mean 分别提高了2.0%、3.2%、5.2%.这说明利用整合模型来处理不同类型的基因组数据是合理的.利用整合模型能够获取数据之间的异质性.iNMF 的平均值比jNMF 分别提高了0.4%、1.2%、0.7%.这说明在iNMF考虑到异构效应引入异构惩罚项是合理的.对于iONMF 方法,施加了正交约束后,模型的聚类性能提高不大,可能是因为正交约束更适合高维数据的聚类,需要进一步的验证.iGNMF 在ACC、ARI、NMI 上的平均值比jNMF 分别提高了1.1%、3.8%、2.6%.这说明图正则化能够很好的保留数据之间的局部几何结构,引入图正则化约束能够很好的提高算法的聚类性能.此外,iRSNMF 在ACC、ARI、NMI 上的平均值比jNMF 分别提高了3.8%、6.2%、4.2%.这表明,iRSNMF 中的结构化项能够很好地保留不同数据类型之间的潜在公共信息,以获取相似的基矩阵.因此,在模型中引入结构化项是合理的.
2)从结果来看,SVD 在4 个数据集上的聚类性能最差,而且该方法在这4 个数据集上的聚类效果类似.这说明SVD 在这4 个数据集上分解出来的右奇异值矩阵不好.
3)结果表明,这5 种整合模型在PEC、PHC、EHC 这3 个数据集上的聚类性能要明显高于PEH 数据集,且在这3 个数据集上的聚类性能差异不大.由于这3 个整合数据集均包含COAD 数据,因此可以推测COAD 数据的样本具有较好的可分性.
4)观察表中数据,可以发现与其他整合方法相比,iRSNMF 模型的方差较小.这说明该模型聚类性能稳定,是因为该模型中施加了稀疏约束可以减小冗余特征的影响,进而提高算法的鲁棒性.
5)表3∼6 表明,在ACC、ARI、NMI 上,iRSNMF 比其他方法至少提高了2.7%、2.4%、1.64%.这是因为iRSNMF 模型引入了结构化项和稀疏约束,它不仅提高了算法的鲁棒性,还通过最小化所有视图的基矩阵的差异来保留数据之间的同质性,进而增强了整合模型的同质效应.所以,聚类结果进一步验证了iRSNMF 方法的合理性和有效性.
3.5 网络构建
全基因组数据的发展为生物信息学的研究提供了更多的机遇,利用生物网络对基因组数据进行分析以挖掘更多的信息成为研究热点[16].基因共表达网络是以基因之间的相关性为基础构建起来的.在网络中,节点代表基因,节点之间的边代表对应基因之间的相互作用关系.本节将皮尔森系数(Pearson correlation coefficient,PCC)作为衡量节点之间相关性的指标,然后对基因之间的相关性进行排序和曲线拟合,选取曲线拟合的第一个拐点作为阈值以过滤相关性较小的基因对,进而获取最终的网络.
在基因共表达网络构建完成以后,根据网络中各个基因的属性对基因进行筛选.我们希望筛选出来的这些基因在癌症的发生和发展机制中起重要作用.为此,设置了一个评估指标S来综合评估各个节点的重要性.该指标定义如下:

式中,B为某一节点的介数,用于评估该节点在维持网络紧密度中的重要程度.Q为某一节点的聚类系数,用于评估某些节点之间连接的密集程度.B和Q的值越大,表明该节点越重要.C表示某节点对于网络中心的接近程度,它的值越小,则该节点越重要.
3.6 构网结果分析
本节以PEH 数据集为例,分别利用5 种整合模型构建基因共表达网络.根据构网结果和评估指标S分别为每种方法筛选出前10、50、100 个基因并与GeneCards(http://www.genecards.org/)中PAAD、ESCA、HNSC 的相关基因比对.表7给出了每种方法选出的基因中同时与3 个癌症的相关基因库匹配成功的基因个数.从结果来看,我们的方法选出的基因在相关基因库中所占的比例更高.为了使结果更清晰,以韦恩图的形式给出了每种方法筛选出的前100个基因在对应癌症的相关基因中找到的个数,如图4所示.
此外,利用iRSNMF 方法构建的基因共表达网络如图5所示,仅保留了节点个数大于20 的3 个模块.表8给出了iRSNMF 挑选出的前10 个基因.为了增强这些基因的生物学解释,通过查阅文献对其进行了验证.其中,有9 个基因在文献中得到验证.

表7 不同方法选出的基因匹配成功的基因数目Table 7 Number of genes matched successfully by different methods

图4 不同方法的前100 个基因在对应癌症的相关基因中找到的数目Figure 4 Number of the first 100 genes found by different methods in the corresponding genes of the corresponding cancer
已有报道表明,RPL34 的表达与胰腺癌的肿瘤分期和肿瘤转移正相关,而且它的沉默可有效抑制胰腺癌的发生、增殖及迁移[17].作为癌基因,RPL34 可以调节食道中恶性肿瘤细胞的增殖和迁移[18].因此,RPL34 是胰腺癌和食道癌的潜在生物标志物和治疗靶标[17-18].此外,已有数据表明RPL34 的过表达对胃癌和非小细胞肺癌细胞的恶性增殖起促进作用[19].在肝内胆管癌中,基因TFDP1 起着致癌作用,其循环扩增可以作为独立的的不良预后指标,是潜在的治疗靶标.在肝癌中,TFDP1 的过表达可能通过上调细胞周期蛋白E1 的表达而对肿瘤发生起促进作用[20].TFDP1 是肺癌的候选癌基因[21],TFDP1 的过表达在肝细胞癌和乳腺癌的肿瘤增殖的过程中起重要作用.它可以通过诱导肿瘤增殖来促进癌症的发展[22].已有文献证明,MMP3 的多态性与食管鳞状细胞癌的易感性密切相关[23].HspA1A 对肿瘤细胞的产生和生长起促进作用[24].它在肝癌的发展中能够促进肿瘤细胞增殖并具有抗凋亡的作用,进而促进肝癌生长.因此探索HSPA1A 的分子机制对抗癌治疗具有潜在用途[25].据报道,IFIT3 是一种原癌基因[26],其过表达会促进胰腺癌细胞的生长,转移并增强胰腺癌细胞的耐药性.此外,IFIT3 与食管癌的发生密切相关[27].因此,IFIT3 可能是诊断胰腺癌和食管癌的新型生物标志物.相关研究表明,ADH5 可能在非小细胞肺癌的发生过程中起致癌作用,是胰腺癌和非小细胞肺癌的潜在预后标志物[28-29].COL4A1 在食管癌中高水平表达并可能与食管癌的预后有关[30].此外,COL4A1 是头颈麟癌潜在的治疗靶基因[31].在肾透明细胞癌中,RPS19 显著高表达并与该癌症的发生和发展密切相关[32].此外,RPS19 编码的蛋白具有免疫抑制特性,降低其免疫抑制会延缓肿瘤的发展.基因CDK16 在癌细胞增殖和抗凋亡中起关键作用[33].在肝癌中,CDK16 是真正的致癌基因,它能够促进肿瘤细胞增殖并抑制细胞凋亡.所以,CDK16 是肝癌的重要治疗靶标和预后指标.此外,CDK16 在食管癌不同类型的组织中选择性表达,而且其高表达与食管鳞癌的发生、发展密切相关.因此,研究这些重要基因对于未来癌症的诊断和治疗以及预后都有着重要意义.
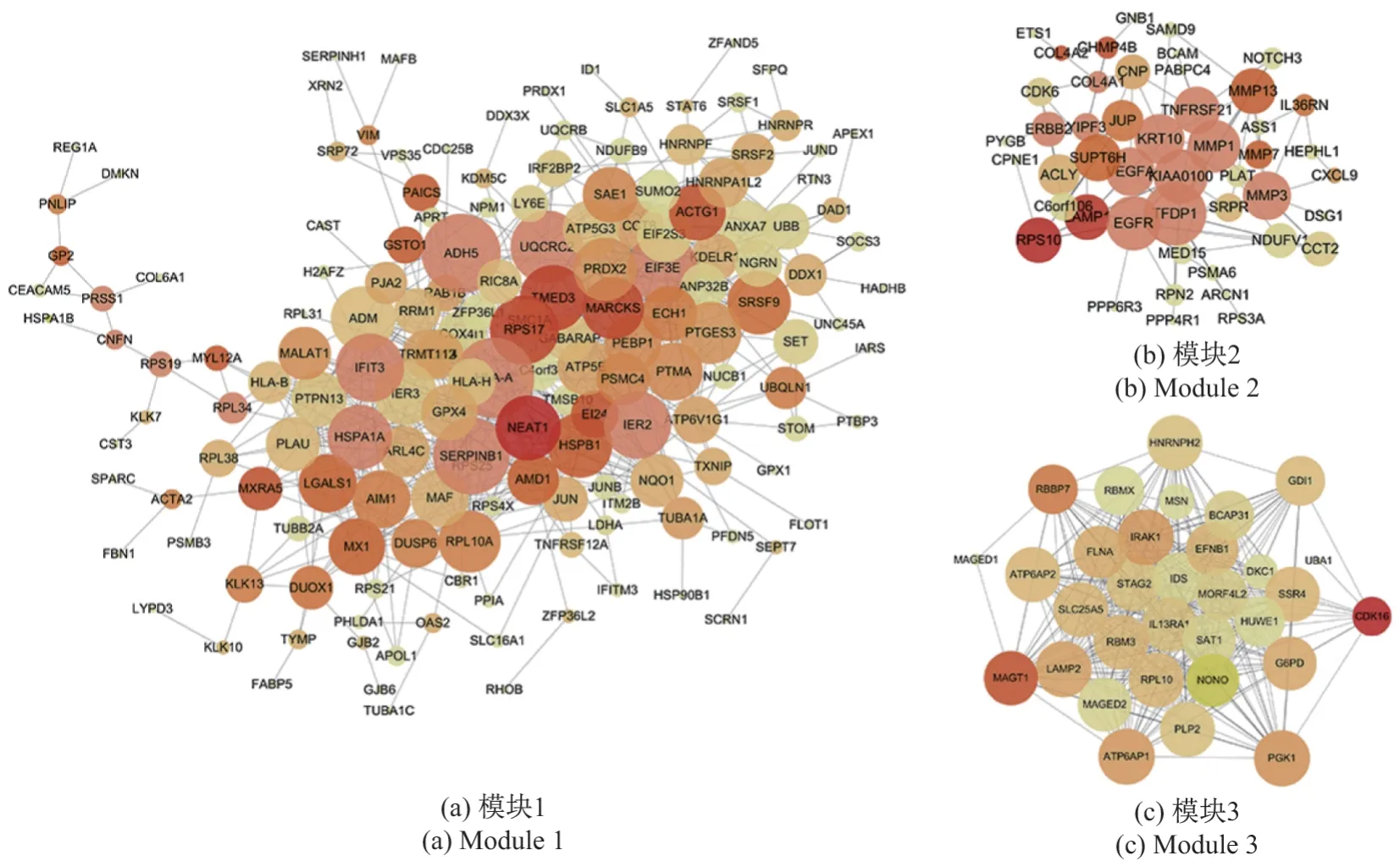
图5 基因共表达网络Figure 5 Gene co-expression network
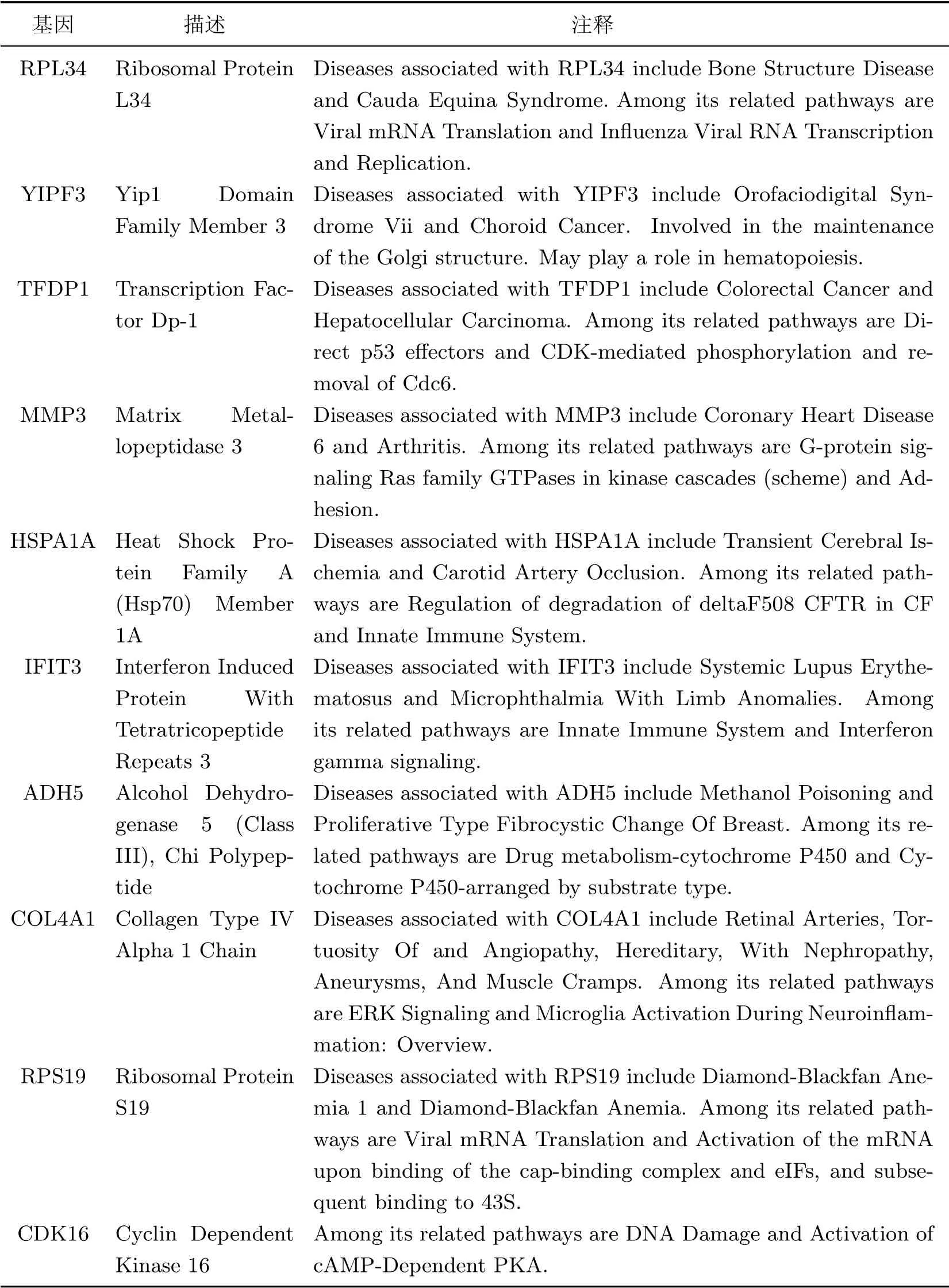
表8 前10 个基因的详细信息Table 8 Details of the first ten genes

图6 功能分组网络Figure 6 Functional grouping network
为了进一步发现网络中的基因的生物功能,利用Cytoscape 对这些基因进行了京都基因与基因组百科全书(Kyoto Encyclopedia of Genes and Genomes,KEGG)富集分析并构建了功能分组网络.富集程度最高的前5 个通路的详细信息如表9所示.功能分组网络可以根据相关基因的相似性来展示术语之间的关系[34],如图6所示.其中,红色标签的节点代表基因,其他颜色标签对应的节点代表的是通路.基因和通路之间的连线代表二者相关.不难发现,网络中有许多基因与多个通路相关并起着桥梁的作用.与多个通路有关的基因可能在生物体的生长过程中起重要作用,应进一步进行探究.在分组网络中,通路节点的大小代表基因在该通路的富集程度,颜色代表该通路隶属于哪一个功能组.具有相同功能的通路,其对应的节点被赋予了相同的颜色[34].其中,彩色标签的通路是其所属功能组中富集程度最显著的通路,组内其他的通路标签颜色为灰色.

表9 前5 个通路的详细信息Table 9 Details of the first five pathways
已有文献表明,核糖体(Ribosome)在生物体的遗传信息处理和翻译工作中起作用,核糖体生物发生是增殖细胞中主要的代谢需求,核糖体生物发生过程中的改变可能会下调细胞的抑癌潜能进而导致癌症的发生[35].吞噬体(Phagosome)与细胞的运输和分解代谢密切相关,它的作用过程是细胞吸收较大颗粒的过程,是抵抗传染原、炎症及组织重塑的主要机制.吞噬体的成熟涉及与其他膜细胞器的调控,包括与自体和溶酶体的相互作用[36].吞噬体和溶酶体的融合过程中会释放出有毒的产物,该产物能够杀死大多数细菌并将其降解为碎片.因而,了解吞噬体的分子机制对开发新疗法以克服由病原体引起的疾病十分重要.松弛素信号通路(Relaxin signaling pathway)主要作用于内分泌系统.最初松弛素被鉴定为妊娠的肽激素在人体中发挥多种作用,包括血管舒张、抗纤维化及血管生成作用.此外,松弛素通过增强肿瘤血管和诱导细胞增殖的能力来促进前列腺癌细胞的生长,而松弛素信号传导可有助于促进肿瘤生长和转移的特征性机制,这在癌症的发生和发展中起重要作用[37].
4 结 语
本文提出了一种新颖的整合模型,称为整合鲁棒结构化非负矩阵分解(iRSNMF)模型.iRSNMF 模型引入了一个结构化项,该项能够通过提高基矩阵之间的一致性来保留数据之间的同质性,进而提高模型的同质效应.同时,该模型对公共系数矩阵施加了L2,1范数约束,这在一定程度上减小了冗余特征的影响,提高了算法的鲁棒性.在实验部分,将iRSNMF 模型用于癌症样本聚类和基因共表达网络分析.首先,采用经典的降维算法和多个整合模型作为对比方法进行聚类实验.然后,利用这几个整合模型分别构建基因共表达网络并挖掘关键基因.最后,通过已有的文献对挖掘到的基因和通路进行分析和验证,并给出相关基因和通路的生物学解释.实验结果表明,iRSNMF 方法具有更好的聚类性能,并且筛选出了更多的癌症相关基因.通过深入研究挖掘到的关键基因和通路能更好地了解它们在癌症中的作用,可以为以后癌症诊断和临床治疗提供新的思路.
